- Books Name
- Kaysons Academy Maths Foundation Book
- Publication
- Kaysons Publication
- Course
- JEE
- Subject
- Maths
Chapter -9
Areas Of Parallelograms And Triangles
You may recall that the part of the plane enclosed by a simple closed figure is called a planar region corresponding to that figure. The magnitude or measure of this planar region is called its area. This magnitude or measure is always expressed with the help of a number (in some unit) such as 5 cm2, 8 m2, 3 hectares etc. So, we can say that area of a figure is a number (in some unit) associated with the part of the plane enclosed by the figure.
We are also familiar with the concept of congruent figures from earlier classes and from Chapter 7. Two figures ar e called congruent, if they have the same shape and the same size. In other words, if two figures A and B are congruent (see Fig), then using a tracing paper,
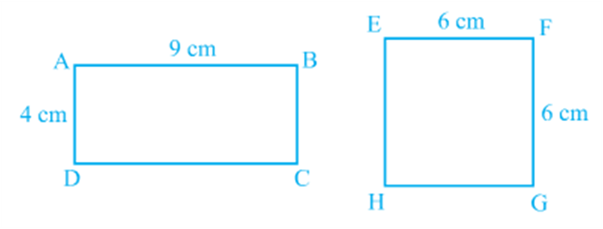
You can superpose one figure over the other such that it will cover the other completely. So if two figures A and B are congruent, they must have equal areas. However, the converse of this statement is not true. In other words, two figures having equal areas need not be congr uent. For example, in Fig, rectangles ABCD and EFGH have equal areas (9 × 4 cm2 and 6 × 6 cm2) but clearly they are not congruent. (Why?)
Now let us look at Fig. given below:
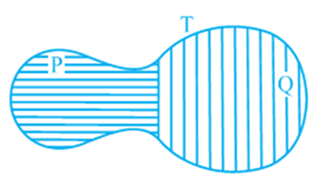
You may observe that planar region formed by figure T is made up of two planar regions formed by figures P and Q. You can easily see that
Area of figure T = Area of figure P + Area of figure Q.
You may denote the area of figure A as ar(A), area of figure B as ar(B), area of figure T as ar(T), and so on. Now you can say that area of a figure is a number (in some unit) associated with the part of the plane enclosed by the figure with the following two properties:
(1) If A and B are two congruent figures, then ar(A) = ar(B);
and (2) if a planar region formed by a figure T is made up of two non-overlapping planar regions formed by figures P and Q, then ar(T) = ar(P) + ar(Q).
You are also aware of some formulae for finding the areas of different figures such as rectangle, square, parallelogram, triangle etc., from your earlier classes. In this chapter, attempt shall be made to consolidate the knowledge about these formulae by studying some relationship between the areas of these geometric figures under the condition when they lie on the same base and between the same parallels. This study will also be useful in the understanding of some results on ‘similarity of triangles’.
Figures on the Same Base and Between the Same Parallels
Look at the following figures:
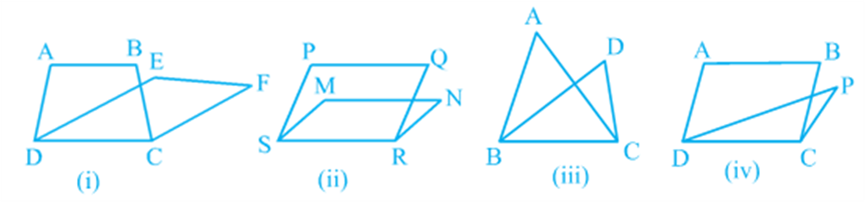
In Fig (i), trapezium ABCD and parallelogram EFCD have a common side DC. We say that trapezium ABCD and parallelogram EFCD are on the same base DC. Similarly, in Fig (ii), parallelograms PQRS and MNRS are on the same base SR; in Fig (iii), triangles ABC and DBC are on the same base BC and in Fig (iv), parallelogram ABCD and triangle PDC are on the same base DC.
Now look at the following figures:
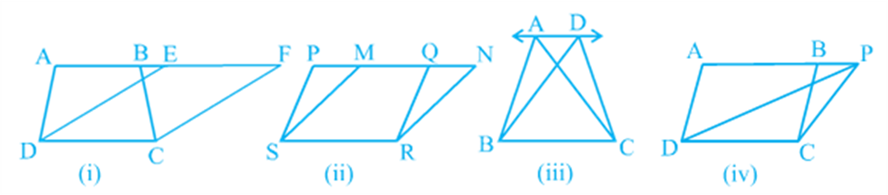
In Fig (i), clearly trapezium ABCD and parallelogram EFCD are on the same base DC. In addition to the above, the vertices A and B (of trapezium ABCD) opposite to base DC and the vertices E and F (of parallelogram EFCD) opposite to base DC lie on a line AF parallel to DC. We say that trapezium ABCD and parallelogram EFCD are on the same base DC and between the same parallels AF and DC. Similarly, parallelograms PQRS and MNRS are on the same base SR and between the same parallels PN and SR [see Fig (ii)] as vertices P and Q of PQRS and vertices M and N of MNRS lie on a line PN parallel to base SR. In the same way, triangles ABC and DBC lie on the same base BC and between the same parallels AD and BC [see Fig (iii)] and parallelogram ABCD and triangle PCD lie on the same base DC and between the same parallels AP and DC [see Fig (iv)].
So, two figures are said to be on the same base and between the same parallels, if they have a common base (side) and the vertices (or the vertex) opposite to the common base of each figure lie on a line parallel to the base. Keeping in view the above statement, you cannot say that Δ PQR and Δ DQR of Fig (i) lie between the same parallels l and QR. Similarly, you cannot say that
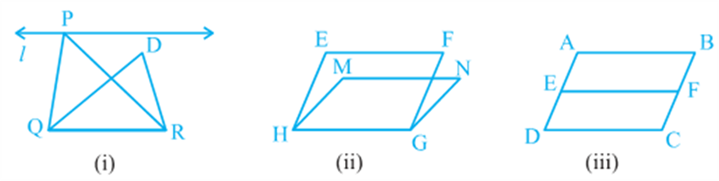
Parallelograms EFGH and MNGH of Fig (ii) lie between the same parallels EF and HG and that parallelograms ABCD and EFCD of Fig (iii) lie between the same parallels AB and DC (even though they have a common base DC and lie between the parallels AD and BC). So, it should clearly be noted that out of the two parallels, one must be the line containing the common base. Note that ΔABC and ΔDBE of Fig (i) are not on the common base. Similarly, ΔABC and parallelogram PQRS of Fig (ii) are also not on the same base.

 Kaysons Publication
Kaysons Publication
