COORDINATE GEOMETRY

Chapter:- 9

COORDINATE GEOMETRY

Introduction
In Class IX, you have studied that to locate the position of a point on a plane, we require a pair of coordinate axes. The distance of a point from the y-axis is called its x-coordinate, or abscissa. The distance of a point from the x-axis is called its y-coordinate, or ordinate. The coordinates of a point on the x-axis are of the form (x, 0), and of a point on the y-axis are of the form (0, y).
Here is a play for you. Draw a set of a pair of perpendicular axes on a graph paper. Now plot the following points and join them as directed: Join the point A(4, 8) to B(3, 9) to C(3, 8) to D(1, 6) to E(1, 5) to F(3, 3) to G(6, 3) to H(8, 5) to I(8, 6) to J(6, 8) to K(6, 9) to L(5, 8) to A. Then join the points P(3.5, 7), Q (3, 6) and R(4, 6) to form a triangle. Also join the points X(5.5, 7), Y(5, 6) and Z(6, 6) to form a triangle. Now join S(4, 5), T(4.5, 4) and U(5, 5) to form a triangle. Lastly join S to the points (0, 5) and (0, 6) and join U to the points (9, 5) and (9, 6). What picture have you got?
Also, you have seen that a linear equation in two variables of the form ax + by + c = 0, (a, b are not simultaneously zero), when represented graphically, gives a straight line. Further, in Chapter 2, you have seen the graph of y = ax₂ + bx + c (a ≠ 0), is a parabola. In fact, coordinate geometry has been developed as an algebraic tool for studying geometry of figures. It helps us to study geometry using algebra, and understand algebra with the help of geometry. Because of this, coordinate geometry is widely applied in various fields such as physics, engineering, navigation, seismology and art!
In this chapter, you will learn how to find the distance between the two points whose coordinates are given, and to find the area of the triangle formed by three given points. You will also study how to find the coordinates of the point which divides a line segment joining two given points in a given ratio.

Distance Formula
Let us consider the following situation:
A town B is located 36 km east and 15 km north of the town A. How would you find the distance from town A to town B without actually measuring it. Let us see. This situation can be represented graphically as shown in Fig. You may use the Pythagoras Theorem to calculate this distance.

 

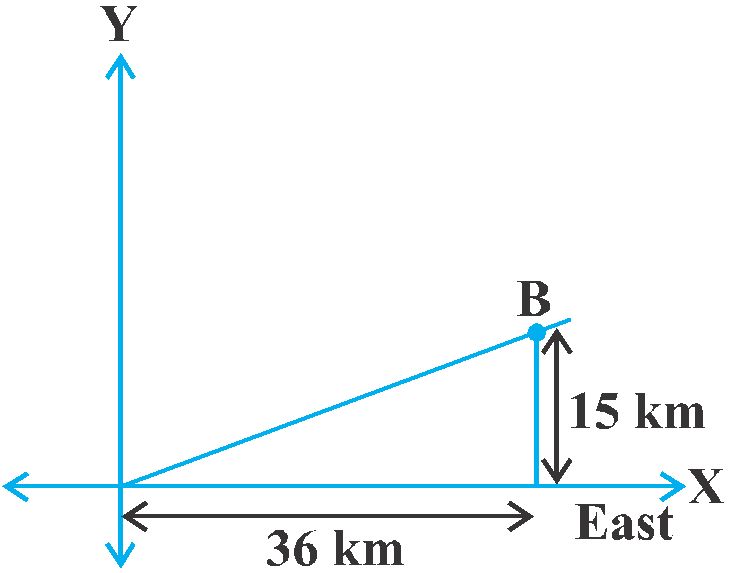
Now, suppose two points lie on the x-axis.
Can we find the distance between them? For instance, consider two points A(4, 0) and B(6, 0) in Fig. The points A and B lie on the x-axis. From the figure you can see that OA = 4 units and OB = 6 units. Therefore, the distance of B from A, i.e., AB = OB – OA = 6 – 4 = 2 units.

 

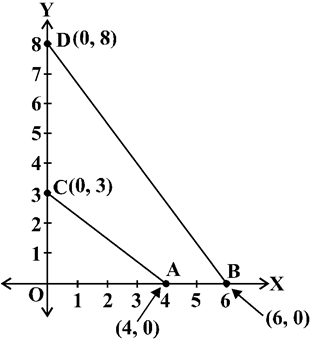
So, if two points lie on the x-axis, we can easily find the distance between them. Now, suppose we take two points lying on the y-axis. Can you find the distance between them. If the points C (0, 3) and D (0, 8) lie on the y-axis, similarly we find that
CD = 8 – 3 = 5 units Next, can you find the distance of A from C (in Fig. 7.2)? Since OA = 4 units and OC = 3 units, the distance of A from C, i.e.,  units. Similarly, you can find the distance of B from D = BD = 10 units.
Let us now find the distance between any two points P(x₁, y₁) and Q (x₂, y₂). Draw R and QS perpendicular to the x-axis. A perpendicular from the point P on QS is rawn to meet it at the point T.
Then, OR = x₁, OS = x₂.   So, RS = x₂ – x₁ = PT.  
Also,  SQ = y₂,  ST = PR = y₁. So, QT = y₂ – y₁.
Now, applying the Pythagoras theorem in ∆PTQ, we get
        PQ² = PT² + QT²
         = (x₂ – x₁)² + (y₂ – y₁)²

Therefore,

Note that since distance is always non-negative, we take only the positive square root. So, the distance between the points P(x₁, y₁) and Q(x₂, y₂) is

Which is called the distance formula.

Remarks:

1. In particular, the distance of a point P(x, y) from the origin O (0, 0) is given by

             

2. We can also write, PQ=

Section Formula

Let us recall the situation in Section 7.2. Suppose a telephone company wants to position a relay tower at P between A and B is such a way that the distance of the tower from B is twice its distance from A. If P lies on AB, it will divide AB in the ratio 1 : 2. If we take A as the origin O, and 1 km as one unit on both the axis, the coordinates of B will be (36, 15). In order to know the position of the tower, we must know the coordinates of P. How do we find these coordinates?

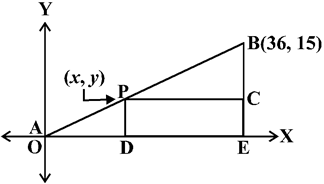
Let the coordinates of P be (x, y). Draw perpendiculars from P and B to the x-axis, meeting it in D and E, respectively. Draw PC perpendicular to BE. Then, by the AA similarity criterion, studied in Chapter 6, ∆POD and ∆BPC are similar.

Therefore, 

So,

These equations give x = 12 and y = 5.
You can check that P(12, 5) meets the condition that OP : PB = 1 : 2.
Now let us use the understanding that you may have developed through this example to obtain the general formula.
Consider any two points A(x₁, y₁) and B(x₂, y₂) and assume that P(x, y) divides AB internally in the ratio m₁ : m₂, i.e.,
Draw AR, PS and BT perpendicular to the x-axis. Draw AQ and PC parallel to the x-axis. Then, by the AA similarity criterion,
                                    ∆PAQ ~ ∆BPC

Therefore,                 PABP=AQPC=PQBC                                                  (1)
Now,                           AQ = RS = OS – OR = x – x₁
                                 PC = ST = OT – OS = x₂ – x
                              PQ = PS – QS = PS – AR = y – y₁
                                BC = BT – CT = BT – PS = y₂ – y

Substituting these values in (1), we get

Taking       

Similarly, taking      

 

So, the coordinates of the point P(x, y) which divides the line segment joining the points A(x₁, y₁) and B(x₂, y₂), internally, in the ratio m₁ : m₂ are
                                          (2)
This is known as the section formula.
This can also be derived by drawing perpendiculars from A, P and B on the y-axis and proceeding as above.
If the ratio in which P divides AB is k : 1, then the coordinates of the point P will be

Special Case: The mid-point of a line segment divides the line segment in the ratio 1 : 1. Therefore, the coordinates of the mid-point P of the join of the points A(x₁, y₁) and B(x₂, y₂) is

Let us solve a few examples based on the section formula.

Area of a Triangle

In your earlier classes, you have studied how to calculate the area of a triangle when its base and corresponding height (altitude) are given. You have used the formula:

In Class IX, you have also studied Heron’s formula to find the area of a triangle. Now, if the coordinates of the vertices of a triangle are given, can you find its area? Well, you could find the lengths of the three sides using the distance formula and then use Heron’s formula. But this could be tedious, particularly if the lengths of the sides are irrational numbers. Let us see if there is an easier way out.

Let ABC be any triangle whose vertices are A(x₁, y₁), B(x₂, y₂) and C(x₃, y₃). Draw AP,
BQ and CR perpendiculars from A, B and C, Respectively, to the x-axis. Clearly ABQP,
APRC and BQRC are all trapzia.
Now, from Fig. it is clear that
Area of ∆ABC = area of trapezium ABQP + area of trapezium APRC – area of trapezium BQRC.
You also know that the Area of a trapezium =  (sum of parallel sides) (distance between them)

Therefore,

Area of ∆ABC =

                  

    

Thus, the area of ∆ABC is the numerical value of the expression

Let us consider a few examples in which we make use of this formula.