Circles and Its Related Terms: A Review

Chapter -10

Circles

Circles and Its Related Terms: A Review

Take a compass and fix a pencil in it. Put its pointed leg on a point on a sheet of a paper. Open the other leg to some distance. Keeping the pointed leg on the same point, rotate the other leg through one revolution. What is the closed figure traced by the pencil on paper? As you know, it is a circle (see Fig). How did you get a circle? You kept one point fixed (A in Fig) and drew all the points that were at a fixed distance from A. This gives us the following definition:

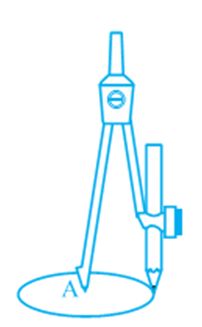
The collection of all the points in a plane, which are at a fixed distance from a fixed point in the plane, is called a circle.
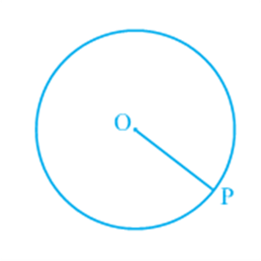
The fixed point is called the centre of the circle and the fixed distance is called the radius of the circle. In Fig, O is the centre and the length OP is the radius of the circle.
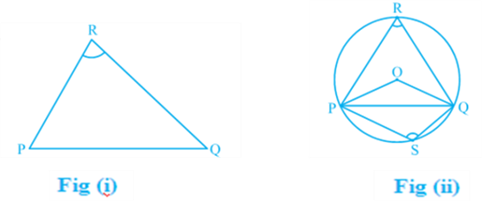
Angle Subtended by a Chord at a Point Take a line segment PQ and a point R not on the line containing PQ. Join PR and QR (see Fig (i)). Then ∠ PRQ is called the angle subtended by the line segment PQ at the point R. What are angles POQ, PRQ and PSQ called in Fig (ii)? ∠ POQ is the angle subtended by the chord PQ at the centre O, ∠ PRQ and ∠ PSQ are respectively the angles subtended by PQ at points R and S on the major and minor arcs PQ.

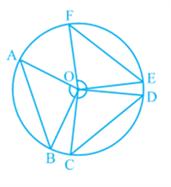
Let us examine the relationship between the size of the chord and the angle subtended by it at the centre. You may see by drawing different chords of a circle and angles subtended by them at the centre that the longer is the chord, the bigger will be the angle subtended by it at the centre. What will happen if you take two equal chords of a circle? Will the angles subtended at the centre be the same or not?
Draw two or more equal chords of a circle and measure the angles subtended by them at the centre (see Fig). You will find that the angles subtended by them at the centre are equal. Let us give a proof of this fact.

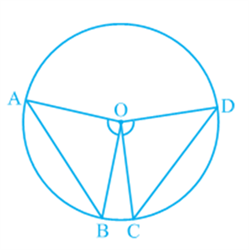
Theorem: Equal chords of a circle subtend equal angles at the centre.
Proof: You are given two equal chords AB and CD of a circle with centre O (see Fig). You want to prove that ∠ AOB = ∠ COD. In triangles AOB and COD,

In triangles AOB and COD,
                   OA = O C     (Radii of a circle)
                   OB = OD       (Radii of a circle)
                    AB = C D                      (Given)
Therefore,   Δ AOB ≅ Δ COD       (SSS rule)
This gives    ∠ AOB = ∠ COD
 (Corresponding parts of congruent triangles).

Which is denoted by R.? Therefore, a real number is either rational or irrational. So, we can say that every real number is represented by a unique point on the number line. Also, every point on the number line represents a unique real number. This is why we call the number line, the real number line.

A circle divides the plane on which it lies into three parts. They are: (i) inside the circle, which is also called the interior of the circle; (ii) the circle and (iii) outside the circle, which is also called the exterior of the circle (see Fig). The circle and its interior make up the circular region.