- Books Name
- Kaysons Academy Chemistry Book
- Publication
- Kaysons Publication
- Course
- JEE
- Subject
- Chemistry
PHOTOELECTRIC EFFECT
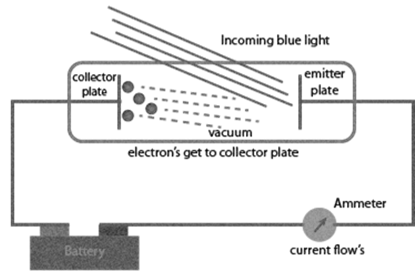
Experimental results observed for the experiment of Photoelectric effect observed by Hertz:
a. When beam of light falls on a metal surface electrons are ejected immediately i.e. there is not time lag between light striking metal surface and ejection of electrons
b. Number of electrons ejected is proportional to intensity or brightness of light
c. Threshold frequency ( no ): For each metal there is a characteristic minimum frequency below which photoelectric effect is not observed. This is called threshold frequency.
d. If frequency of light is less than the threshold frequency there is no ejection of electrons no matter how long it falls on surface or how high is its intensity.
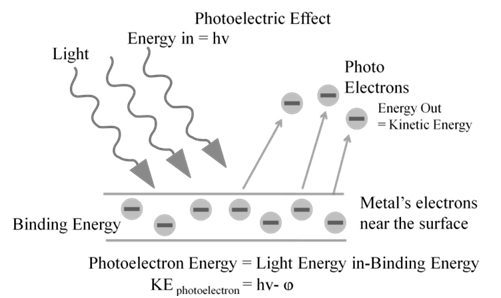
Photoelectric work function (Wo): The minimum energy required to eject electrons is called photoelectric work function. Wo= h no
Energy of the ejected electrons: ½ mev2 = h(n-no)
The kinetic energies of these electrons increase with the increase of frequency of the light used. All the above results could not be explained on the basis of laws of classical physics.
Photoelectric work function (Wo): The minimum energy required to eject electrons is called photoelectric work function. Wo= h no
Energy of the ejected electrons: ½ mev2 = h(n-no)
DUAL BEHAVIOUR OF ELECTROMAGNETIC RADIATION
It is concluded from active experiment that electromagnetic radiation have due nature. Wave nature as confirmed by experiments and particle nature is confirmed by photo electric effect.
de Broglie proposed that matter exhibits dual behaviour i.e. matter shows both particle and wave nature.
1. de Broglie’s relation: l = ![]() =
=![]()
Where: l - Wavelength; p – Momentum; v – Velocity; h – Planck’s constant
2. According to de Broglie, every object in motion has a wave character. Wavelengths of macroscopic objects cannot be detected but for microscopic particles it can be detected. This is because for microscopic objects, the mass is less. Since mass and wavelength are inversely proportional to each other, the wavelength will be more. But for macroscopic objects, the mass is large. Therefore, wavelength will be too short to be detected. Dual
Heisenberg’s uncertainty principle
It states that it is impossible to determine simultaneously, the exact position and exact momentum (or velocity) of an electron
![]()
Assuming mass is constant and does not change with velocity
![]()
Schrodinger wave equation
![]()
The probability of finding an electron at a point within an atom is proportional to the square of the orbital wave function i.e., ψ2 at that point. ψ2 is known as probability density and is always positive. From the value of ψ2 at different points within an atom, it is possible to predict the region around the nucleus where electron will most probably be found
IMPORTANT FEATURES OF THE QUANTUM MECHANICAL MODEL OF ATOM
Quantum mechanical model of atom is the picture of the structure of the atom, which emerges from the application of the Schrödinger equation to atoms. The following are the important features of the quantum me chemical model of atom:
1. The energy of electrons in atoms is quantized (i.e., can only have certain specific values), for example when electrons are bound to the nucleus in atoms.
2. The existence of quantized electronic energy levels is a direct result of the wave like properties of electrons and is allowed solutions of Schrödinger wave equation.
3. Both the exact position and exact velocity of an electron in an atom cannot be determined simultaneously (Heisenberg uncertainty principle). The path of an electron in an atom therefore, can never be determined or known accurately. That is why, as you shall see later on, one talks of only probability of finding the electron at different points in an atom.
4. An atomic orbital is the wave function ψ for an electron in an atom. Whenever an electron is described by a wave function, we say that the electron occupies that orbital. Since many such wave functions are possible for an electron, there are many atomic orbitals in an atom. These one electron orbital wave functions. or orbitals form the basis of the electronic structure of atoms. In each orbital, the electron has a definite energy. An orbital cannot contain more than two electrons. In a multi-electron atom, the electrons are filled in various orbitals in the order of increasing energy. For each electron of a multi-electron atom, there shall, therefore, be an orbital wave function characteristic of the orbital it occupies. All the information about the electron in an atom is stored in its orbital wave function ψ and quantum mechanics makes it possible to extract this information out of ψ.

 Kaysons Publication
Kaysons Publication
