- Books Name
- Kaysons Academy Chemistry Book
- Publication
- Kaysons Publication
- Course
- JEE
- Subject
- Chemistry
ORBITALS AND QUANTUM NUMBERS

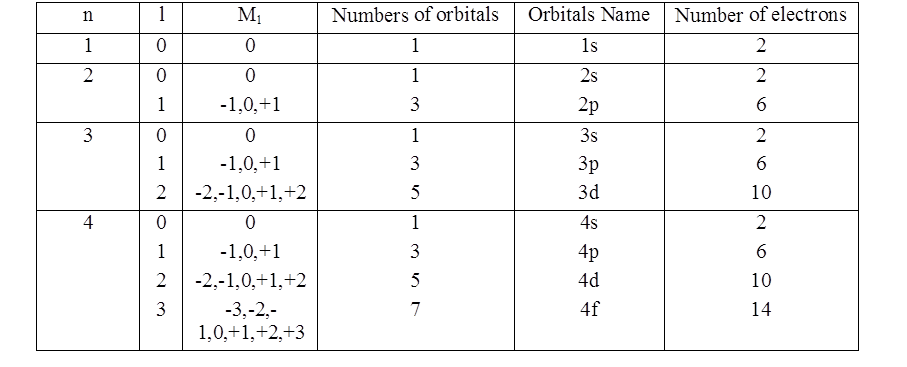
ORBIT VS. ORBITAL

PHYSICAL SIGNIFICANCE OF THE QUANTUM NUMBERS
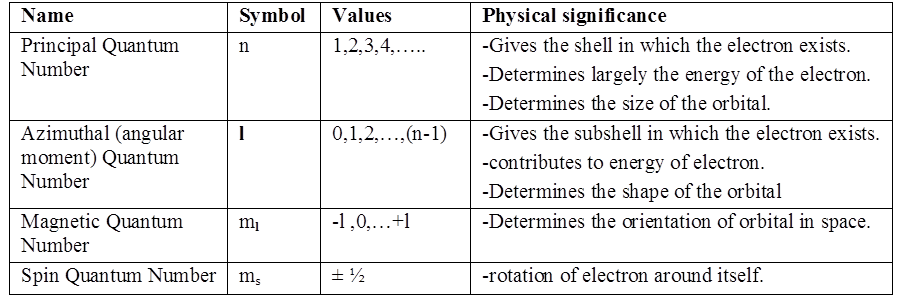
1s and 2s orbitals

2s and 2p Orbitals
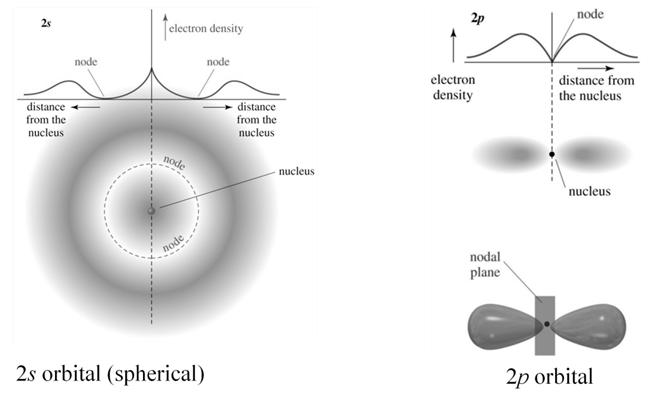
d orbital
ELECTRONIC CONFIGURATION OF ATOMS
Aufbau principle Electrons are placed in the lowest energetically available subshell. Thus orbitals are filled in the order of increasing energy, using two general rules to help predict electronic configurations:-
- Electrons are assigned to orbitals in order of increasing value of (n+ℓ). Orbitals with lower value of (n+l) are filled first as they have lower energy.
- For subshells with the same value of (n+ℓ), electrons are assigned first to the sub shell with lower n.
- The order in which the orbitals are filled is as follows:
- 1s, 2s, 2p, 3s, 3p, 4s, 3d, 4p, 5s, 4d, 5p, 4f, 5d, 6p, 7s...
- It is based on (n+ l) rule. It states that the orbital with lower value of (n +l) has lower energy.
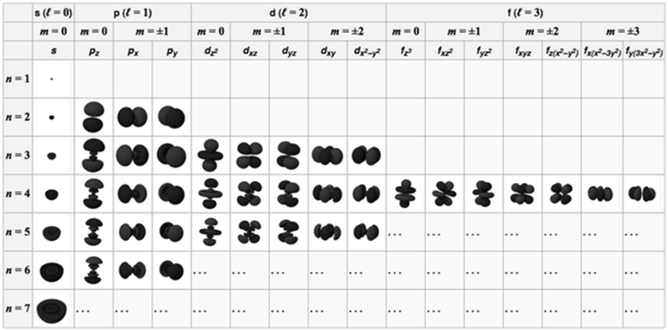
AUFBAU DIAGRAM
PAULI'S EXCLUSION PRINCIPLE
It is impossible for any two electrons of an atom to have the same values of the all four quantum numbers. If even three quantum numbers are same for any two electrons of the atom then fourth quantum number will definitely be different.
In other words an orbital can have maximum of two electrons
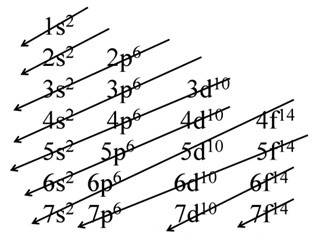
Hund’s Rule of Maximum Multiplicity
This rule deals filling of electrons in the orbitals belonging to the same subshells of equal energy called degenerate orbitals.
- It states that pairing of electrons in the orbitals belonging to the same sub shell (p, d or f) does not take place until each orbital of that sub shell gets one electron that is singly occupied.
- Some of the orbitals acquire extra stability due to their symmetry.
EXCEPTION: HALF-FILLED AND FILLED D ORBITALS
- When a subshell is half-filled or completely filled, it lowers the overall energy of the atom.
- In other words, this is favoured.
- This usually doesn't affect electron configurations, except in the d and f subshells.
- Example: Copper (29 electrons)
- Normal electron configuration:
1s22s22p63s23p64s23d9
- Added stability if 3 d is full (electron gets promoted to 3 d from 4s)
- 1s22s22p63s23p64s13d10
The region where this probability density function reduces to zero is called nodal surfaces or simply nodes.
Boundary surface diagram: In this representation, a boundary surface or contour surface is drawn in space for an orbital on which the value of probability density ψ 2(r) is constant. However, for a given orbital, only that boundary surface diagram of constant probability density is taken to be good representation of the shape of the orbital which encloses a region or volume in which the probability of finding the electron is very high, say, 90%.
Radial nodes: Radial nodes occur when the probability density wave function for the electron is zero on a spherical surface of a particular radius. Number of radial nodes = n – l – 1
Angular nodes: Angular nodes occur when the probability density wave function for the electron is zero along the directions specified by a particular angle. Number of angular nodes = l
Total number of nodes = n – 1
Degenerate orbitals: Orbitals having the same energy are called degenerate orbitals
IMPORTANT FORMULAE
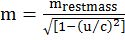
- Frequency of electromagnetic wave
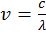
- Energy of photon E = hn =
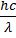
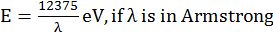
- Bohr’s postulate mvr =
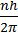 (Angular momentum of ‘e’ in an orbit)
(Angular momentum of ‘e’ in an orbit) 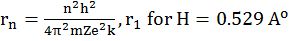
- rn = r1 x n2 same atom different orbit
- rZ = rH / Z same orbit different atom
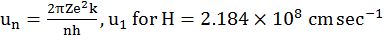
- un = u1 / n same atom different orbit
- uZ = uH x Z same orbit different atom
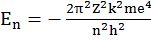 E1 for H= -21.72X10-12 erg = -13.6 eV
E1 for H= -21.72X10-12 erg = -13.6 eV- En = E1/n2 same atom different orbit
- EZ = EH x Z2 same orbit different atom
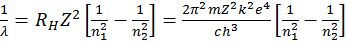
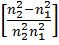 Ao
Ao- Ön=a (Z – b), where n is frequency of X-rays given out by metal of at. No. Z
- Average atomic weight =
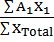
- KE of photoelectric electron (½ mv2) = hn - hno (hno = work function) & no threshold frequency
- deBroglie equation l =
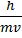
- Uncertainty
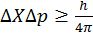
- (Schrodinger wave equation)
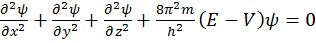
- Angular momentum of ‘e’ in an orbital=
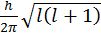
- Magnetic moment of an atom=.
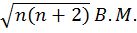 where n is no. of unpaired electrons
where n is no. of unpaired electrons - Nodes
- Radial (spherical) nodes=(n – l – 1)
- Angular (non spherical) nodes=l
- Total nodes= (n - 1)
- No of spectral lines =
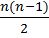

 Kaysons Publication
Kaysons Publication
