Linear Equation
- Books Name
- ABCD CLASSES Mathematics Book
- Publication
- ABCD CLASSES
- Course
- CBSE Class 9
- Subject
- Mathmatics
Linear equation in two variables
Linear Equations
Linear equations are equations of the first order. The linear equations are defined for lines in the coordinate system. When the equation has a homogeneous variable of degree 1 (i.e. only one variable), then it is known as a linear equation in one variable. A linear equation can have more than one variable. If the linear equation has two variables, then it is called linear equations in two variables and so on. Some of the examples of linear equations are 2x – 3 = 0, 2y = 8, m + 1 = 0, x/2 = 3, x + y = 2, 3x – y + z = 3. In this article, we are going to discuss the definition of linear equations, standard form for linear equation in one variable, two variables, three variables and their examples with complete explanation.
Linear Equation Definition
An equation is a mathematical statement, which has an equal sign (=) between the algebraic expression. Linear equations are the equations of degree 1. It is the equation for the straight line. The solutions of linear equations will generate values, which when substituted for the unknown values, make the equation true. In the case of one variable, there is only one solution. For example, the equation x + 2 = 0 has only one solution as x = -2. But in the case of the two-variable linear equation, the solutions are calculated as the Cartesian coordinates of a point of the Euclidean plane.
Below are some examples of linear equations in one variable, two variables and three variables:
|
Linear Equation in One variable |
Linear Equation in Two variables |
Linear Equation in Three variables |
|
3x+5=0 (3/2)x +7 = 0 98x = 49 |
y+7x=3 3a+2b = 5 6x+9y-12=0 |
x + y + z = 0 a – 3b = c 3x + 12 y = ½ z |
Forms of Linear Equation
The three forms of linear equations are
- Standard Form
- Slope Intercept Form
- Point Slope Form
Now, let us discuss these three major forms of linear equations in detail.
Standard Form of Linear Equation
Linear equations are a combination of constants and variables. The standard form of a linear equation in one variable is represented as
|
ax + b = 0, where, a ≠ 0 and x is the variable. |
The standard form of a linear equation in two variables is represented as
|
ax + by + c = 0, where, a ≠ 0, b ≠ 0 , x and y are the variables. |
Linear Equation
CHAPTER -4
Linear equation in two variables
Linear Equations
Linear equations are equations of the first order. The linear equations are defined for lines in the coordinate system. When the equation has a homogeneous variable of degree 1 (i.e. only one variable), then it is known as a linear equation in one variable. A linear equation can have more than one variable. If the linear equation has two variables, then it is called linear equations in two variables and so on. Some of the examples of linear equations are 2x – 3 = 0, 2y = 8, m + 1 = 0, x/2 = 3, x + y = 2, 3x – y + z = 3. In this article, we are going to discuss the definition of linear equations, standard form for linear equation in one variable, two variables, three variables and their examples with complete explanation.
Linear Equation Definition
An equation is a mathematical statement, which has an equal sign (=) between the algebraic expression. Linear equations are the equations of degree 1. It is the equation for the straight line. The solutions of linear equations will generate values, which when substituted for the unknown values, make the equation true. In the case of one variable, there is only one solution. For example, the equation x + 2 = 0 has only one solution as x = -2. But in the case of the two-variable linear equation, the solutions are calculated as the Cartesian coordinates of a point of the Euclidean plane.
Below are some examples of linear equations in one variable, two variables and three variables:

Forms of Linear Equation
The three forms of linear equations are
- Standard Form
- Slope Intercept Form
- Point Slope Form
Now, let us discuss these three major forms of linear equations in detail.
Standard Form of Linear Equation
Linear equations are a combination of constants and variables. The standard form of a linear equation in one variable is represented as
ax + b = 0, where, a ≠ 0 and x is the variable.
The standard form of a linear equation in two variables is represented as
ax + by + c = 0, where, a ≠ 0, b ≠ 0 , x and y are the variables.
Solution of a linear equation
- Books Name
- ABCD CLASSES Mathematics Book
- Publication
- ABCD CLASSES
- Course
- CBSE Class 9
- Subject
- Mathmatics
Solution of a linear equation
Worked-out examples on solving linear equations are given below. Instructions are given step-by-step with detailed explanation by using addition, subtraction, multiplication and division for solving linear equations.
Examples on Solving Linear Equations:
1. Solve: (2x + 5)/(x + 4) = 1
Solution:
(2x + 5)/(x + 4) = 1
⇒ 2x + 5 = 1(x + 4)
⇒ 2x + 5 = x + 4
⇒ 2x - x = 4 - 5 (Transferring positive x to the left hand side changes to negative x and again, positive 5 changes to negative 5)
⇒ x = -1
Therefore, x = - 1 is the required solution of the equation (2x + 5)/(x + 4) = 1
2. Solve: 6x - 19 = 3x - 10
Solution:
6x - 19 = 3x - 10
⇒ 6x - 3x = - 10 + 19 (Transferring 3x to L.H.S changes to negative 3x and -19 to R.H.S. changes to positive 19)
⇒ 3x = 9
⇒ 3x/3 = 9/3 (Dividing both sides by 3)
⇒ x = 3
3. Solve: 5 - 2(x - 1) = 4(3 - x) - 2x.
Solution:
5 - 2(x - 1) = 4(3 - x) - 2x
⇒ 5 - 2x + 2 = 12 - 4x - 2x (Removing the brackets and then simplify)
⇒ 7 - 2x = 12 - 6x (Transferring -6x to L.H.S. changes to positive 6x and 7 to R.H.S. changes to negative 7)
⇒ -2x + 6x = 12 - 7
⇒ 4x = 5
⇒ 4x/4 = 5/4
⇒ x = 5/4
4. x/2 + x/3 = x - 7
Solution:
x/2 + x/3 = x - 7
Least common multiple of2 and 3 is 6
⇒ (x/2 × 3/3) + (x/3 × 2/2) = x - 7
⇒ 3x/6 + 2x/6 = x - 7
⇒ (3x + 2x)/6 = x - 7
⇒ 5x/6 = x - 7
⇒ 5x = 6(x - 7)
⇒ 5x = 6x - 42 (Transferring 6x to L.H.S. changes to negative 6x)
⇒ 5x - 6x = -42
⇒ -x = -42
⇒ x = 42
5. 2/(x + 3) = 3/(5 - x)
Solution:
2/(x + 3) = 3/(5 - x)
⇒ 3(x + 3) = 2(5 - x) (cross multiply and then remove the brackets)
⇒ 3x + 9 = 10 - 2x (Transferring -2x to L.H.S. changes to positive 2x and 9 to R.H.S. changes to -9)
⇒ 3x + 2x = 10 - 9
⇒ 5x = 1
⇒ 5x/5 = 1/5 (Dividing both sides by 5)
⇒ x = 1/5
Solution of a linear equation
Solution of a linear equation
Worked-out examples on solving linear equations are given below. Instructions are given step-by-step with detailed explanation by using addition, subtraction, multiplication and division for solving linear equations.
Examples on Solving Linear Equations:
1. Solve: (2x + 5)/(x + 4) = 1
Solution:
(2x + 5)/(x + 4) = 1
⇒ 2x + 5 = 1(x + 4)
⇒ 2x + 5 = x + 4
⇒ 2x - x = 4 - 5 (Transferring positive x to the left hand side changes to negative x and again, positive 5 changes to negative 5)
⇒ x = -1
Therefore, x = - 1 is the required solution of the equation (2x + 5)/(x + 4) = 1
2. Solve: 6x - 19 = 3x - 10
Solution:
6x - 19 = 3x - 10
⇒ 6x - 3x = - 10 + 19 (Transferring 3x to L.H.S changes to negative 3x and -19 to R.H.S. changes to positive 19)
⇒ 3x = 9
⇒ 3x/3 = 9/3 (Dividing both sides by 3)
⇒ x = 3
3. Solve: 5 - 2(x - 1) = 4(3 - x) - 2x.
Solution:
5 - 2(x - 1) = 4(3 - x) - 2x
⇒ 5 - 2x + 2 = 12 - 4x - 2x (Removing the brackets and then simplify)
⇒ 7 - 2x = 12 - 6x (Transferring -6x to L.H.S. changes to positive 6x and 7 to R.H.S. changes to negative 7)
⇒ -2x + 6x = 12 - 7
⇒ 4x = 5
⇒ 4x/4 = 5/4
⇒ x = 5/4
4. x/2 + x/3 = x - 7
Solution:
x/2 + x/3 = x - 7
Least common multiple of2 and 3 is 6
⇒ (x/2 × 3/3) + (x/3 × 2/2) = x - 7
⇒ 3x/6 + 2x/6 = x - 7
⇒ (3x + 2x)/6 = x - 7
⇒ 5x/6 = x - 7
⇒ 5x = 6(x - 7)
⇒ 5x = 6x - 42 (Transferring 6x to L.H.S. changes to negative 6x)
⇒ 5x - 6x = -42
⇒ -x = -42
⇒ x = 42
5. 2/(x + 3) = 3/(5 - x)
Solution:
2/(x + 3) = 3/(5 - x)
⇒ 3(x + 3) = 2(5 - x) (cross multiply and then remove the brackets)
⇒ 3x + 9 = 10 - 2x (Transferring -2x to L.H.S. changes to positive 2x and 9 to R.H.S. changes to -9)
⇒ 3x + 2x = 10 - 9
⇒ 5x = 1
⇒ 5x/5 = 1/5 (Dividing both sides by 5)
⇒ x = 1/5
Graph of linear equation in two variables
- Books Name
- ABCD CLASSES Mathematics Book
- Publication
- ABCD CLASSES
- Course
- CBSE Class 9
- Subject
- Mathmatics
Graphing of Linear Equations
Linear equations, also known as first-order degree equations, where the highest power of the variable is one. When an equation has one variable, it is known as linear equations in one variable. If the linear equations contain two variables, then it is known as linear equations in two variables, and so on. In this article, we are going to discuss the linear equations in two variables, and also going to learn about the graphing of linear equations in two variables with examples.
Linear Equations in Two Variables
Equations of degree one and having two variables are known as linear equations in two variables. It is of the form, ax +by +c = 0, where a, b and c are real numbers, and both a and b not equal to zero.
Equations of the form ax+by = 0; where a and b are real numbers, and a,b ≠ 0, is also linear equations in two variable.
Solution of a Linear Equation in Two Variables
The solution of a linear equation in two variables is a pair of numbers, one for x and one for y which satisfies the equation. There are infinitely many solutions for a linear equation in two variables.
For example, x+2y =6 is a linear equation and some of its solution are (0,3),(6,0),(2,2) because, they satisfy x+2y=6.
Graphing of Linear Equation in Two Variables
Since the solution of linear equation in two variable is a pair of numbers (x,y), we can represent the solutions in a coordinate plane.
Consider the equation,
2x+y = 6 —(1)
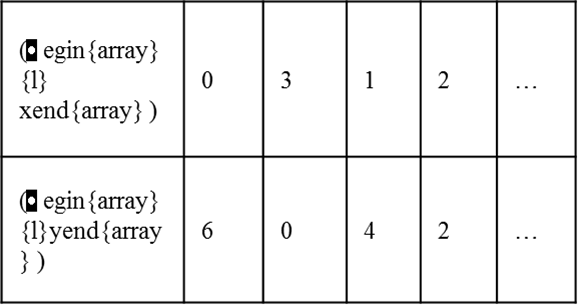
Some solutions of the above equation are, (0,6), (3,0), (1,4), (2,2) because, they satisfy (1).
We can represent the solution of (1) using a table as shown below.
|
\(\begin{array}{l} x\end{array} \) |
0 |
3 |
1 |
2 |
… |
|
\(\begin{array}{l}y\end{array} \) |
6 |
0 |
4 |
2 |
… |
We can plot the above points (0,6), (3,0), (1,4), (2,2) in a coordinate plane (Refer figure).
We can take any two points and join those to make a line. Let the line be PQ. It is observed that all the four points are lying on the same line PQ.
Consider any other point on the line PQ, for example, take point (4,-2) which lies on PQ.
Let’s check whether this point satisfies the equation or not.
Substituting (4,-2) in (1) gives,
LHS=(2×4)-2 = 6= RHS
Therefore (4,-2) is a solution of (1).
Similarly, if we take any point on the line PQ, it will satisfy (1).
It can be observed that,
- All the points say, (p,q) on the line PQ gives a solution of 2x+y = 6.
- All the solution of 2x+y = 6, lie on the line PQ.
- Points which are not the solution of 2x+y = 6 will not lie on the line PQ.
Graph of linear equation in two variables
Graphing of Linear Equations
Linear equations, also known as first-order degree equations, where the highest power of the variable is one. When an equation has one variable, it is known as linear equations in one variable. If the linear equations contain two variables, then it is known as linear equations in two variables, and so on. In this article, we are going to discuss the linear equations in two variables, and also going to learn about the graphing of linear equations in two variables with examples.
Linear Equations in Two Variables
Equations of degree one and having two variables are known as linear equations in two variables. It is of the form, ax +by +c = 0, where a, b and c are real numbers, and both a and b not equal to zero.
Equations of the form ax+by = 0; where a and b are real numbers, and a,b ≠ 0, is also linear equations in two variable.
Solution of a Linear Equation in Two Variables
The solution of a linear equation in two variables is a pair of numbers, one for x and one for y which satisfies the equation. There are infinitely many solutions for a linear equation in two variables.
For example, x+2y =6 is a linear equation and some of its solution are (0,3),(6,0),(2,2) because, they satisfy x+2y=6.
Graphing of Linear Equation in Two Variables
Since the solution of linear equation in two variable is a pair of numbers (x,y), we can represent the solutions in a coordinate plane.
Consider the equation,
2x+y = 6 —(1)
Some solutions of the above equation are, (0,6), (3,0), (1,4), (2,2) because, they satisfy (1).
We can represent the solution of (1) using a table as shown below.
We can plot the above points (0,6), (3,0), (1,4), (2,2) in a coordinate plane (Refer figure).
We can take any two points and join those to make a line. Let the line be PQ. It is observed that all the four points are lying on the same line PQ.
Consider any other point on the line PQ, for example, take point (4,-2) which lies on PQ.
Let’s check whether this point satisfies the equation or not.
Substituting (4,-2) in (1) gives,
LHS=(2×4)-2 = 6= RHS
Therefore (4,-2) is a solution of (1).
Similarly, if we take any point on the line PQ, it will satisfy (1).
It can be observed that,
- All the points say, (p,q) on the line PQ gives a solution of 2x+y = 6.
- All the solution of 2x+y = 6, lie on the line PQ.
- Points which are not the solution of 2x+y = 6 will not lie on the line PQ.
Equations of lines parallel to X-axis and Y-axis
- Books Name
- ABCD CLASSES Mathematics Book
- Publication
- ABCD CLASSES
- Course
- CBSE Class 9
- Subject
- Mathmatics
Equations of lines parallel to X-axis and Y-axis
In two-dimensional coordinate geometry, the coordinate plane is made up of two axes, namely x-axis and y-axis. The horizontal line in the cartesian plane is called x-axis and the vertical line in the cartesian plane is called y-axis. In this article we are going to learn the equations of line parallel to x-axis and y-axis with a complete explanation and many solved examples.
Equations of Line Parallel to X-axis
We know that the equation of x-axis is y=0.
Thus, the equation of line parallel to the x-axis is given by the equation: y = k.
Where “k” is a constant value.
The above equation is considered as the generalized form of line equation parallel to the x-axis.
We can also say that “k” is a real number, and it is the distance from the x-axis to the line y=k.
An example of a line equation parallel to the x-axis is y=5. It can also be written as y-5 =0.
Equations of Line Parallel to Y-axis
The general form of the equation of y-axis is x = 0.
Hence, the equation of line parallel to the y-axis is given by the equation: x = k.
Where “k” is a constant value, which is a real number that represents the distance from the y-axis to the line x =k.
The equation x = k is the generalized form of line equation parallel to y-axis.
An example of an equation of line parallel to the y-axis x = 7, which can also be represented as x – 7 =0.
Equations of Line Parallel to X-axis and Y-axis Examples
Example 1:
Determine the line equation which is parallel to the x-axis at a distance of 5 units above the x-axis.
Solution:
The equation of the straight line parallel to the x-axis is y = k.
Since the distance is 5 units above the x-axis, the value of k is positive.
Thus, the equation of the straight line parallel to the x-axis at a distance of 5 units above the x-axis is y=5.
The above equation can also be written as y-5 =0.
Example 2:
Find the line equation which is parallel to the y-axis at a distance of 10 units right to the y-axis.
Solution:
The equation of the straight line parallel to the y-axis is x = k.
Since the distance is 10 units right to the y-axis, the value of k is positive.
Therefore, the equation of the straight line parallel to the y-axis at a distance of 10 units right to the y-axis is x = 10.
The line equation x =10 can also be written as x -10 = 0.
What is the equation of the x-axis?
The equation of x-axis is y = 0.
What is the equation of the y-axis?
The equation of y-axis is x = 0.
What is the equation of line parallel to the x-axis?
The equation of a line parallel to x-axis y=k, where “k” is a real number.
Equations of lines parallel to X-axis and Y-axis
Equations of lines parallel to X-axis and Y-axis
In two-dimensional coordinate geometry, the coordinate plane is made up of two axes, namely x-axis and y-axis. The horizontal line in the cartesian plane is called x-axis and the vertical line in the cartesian plane is called y-axis. In this article we are going to learn the equations of line parallel to x-axis and y-axis with a complete explanation and many solved examples.
Equations of Line Parallel to X-axis
We know that the equation of x-axis is y=0.
Thus, the equation of line parallel to the x-axis is given by the equation: y = k.
Where “k” is a constant value.
The above equation is considered as the generalized form of line equation parallel to the x-axis.
We can also say that “k” is a real number, and it is the distance from the x-axis to the line y=k.
An example of a line equation parallel to the x-axis is y=5. It can also be written as y-5 =0.
Equations of Line Parallel to Y-axis
The general form of the equation of y-axis is x = 0.
Hence, the equation of line parallel to the y-axis is given by the equation: x = k.
Where “k” is a constant value, which is a real number that represents the distance from the y-axis to the line x =k.
The equation x = k is the generalized form of line equation parallel to y-axis.
An example of an equation of line parallel to the y-axis x = 7, which can also be represented as x – 7 =0.
Equations of Line Parallel to X-axis and Y-axis Examples
Example 1:
Determine the line equation which is parallel to the x-axis at a distance of 5 units above the x-axis.
Solution:
The equation of the straight line parallel to the x-axis is y = k.
Since the distance is 5 units above the x-axis, the value of k is positive.
Thus, the equation of the straight line parallel to the x-axis at a distance of 5 units above the x-axis is y=5.
The above equation can also be written as y-5 =0.
Example 2:
Find the line equation which is parallel to the y-axis at a distance of 10 units right to the y-axis.
Solution:
The equation of the straight line parallel to the y-axis is x = k.
Since the distance is 10 units right to the y-axis, the value of k is positive.
Therefore, the equation of the straight line parallel to the y-axis at a distance of 10 units right to the y-axis is x = 10.
The line equation x =10 can also be written as x -10 = 0.
What is the equation of the x-axis?
The equation of x-axis is y = 0.
What is the equation of the y-axis?
The equation of y-axis is x = 0.
What is the equation of line parallel to the x-axis?
The equation of a line parallel to x-axis y=k, where “k” is a real number.

 ABCD CLASSES
ABCD CLASSES
