Graphing of Linear Equations
Linear equations, also known as first-order degree equations, where the highest power of the variable is one. When an equation has one variable, it is known as linear equations in one variable. If the linear equations contain two variables, then it is known as linear equations in two variables, and so on. In this article, we are going to discuss the linear equations in two variables, and also going to learn about the graphing of linear equations in two variables with examples.
Linear Equations in Two Variables
Equations of degree one and having two variables are known as linear equations in two variables. It is of the form, ax +by +c = 0, where a, b and c are real numbers, and both a and b not equal to zero.
Equations of the form ax+by = 0; where a and b are real numbers, and a,b ≠ 0, is also linear equations in two variable.
Solution of a Linear Equation in Two Variables
The solution of a linear equation in two variables is a pair of numbers, one for x and one for y which satisfies the equation. There are infinitely many solutions for a linear equation in two variables.
For example, x+2y =6 is a linear equation and some of its solution are (0,3),(6,0),(2,2) because, they satisfy x+2y=6.
Graphing of Linear Equation in Two Variables
Since the solution of linear equation in two variable is a pair of numbers (x,y), we can represent the solutions in a coordinate plane.
Consider the equation,
2x+y = 6 —(1)
Some solutions of the above equation are, (0,6), (3,0), (1,4), (2,2) because, they satisfy (1).
We can represent the solution of (1) using a table as shown below.
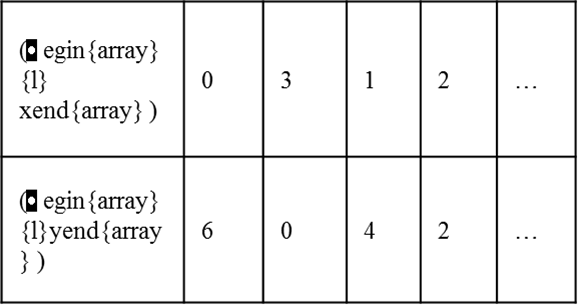
We can plot the above points (0,6), (3,0), (1,4), (2,2) in a coordinate plane (Refer figure).
We can take any two points and join those to make a line. Let the line be PQ. It is observed that all the four points are lying on the same line PQ.
Consider any other point on the line PQ, for example, take point (4,-2) which lies on PQ.
Let’s check whether this point satisfies the equation or not.
Substituting (4,-2) in (1) gives,
LHS=(2×4)-2 = 6= RHS
Therefore (4,-2) is a solution of (1).
Similarly, if we take any point on the line PQ, it will satisfy (1).
It can be observed that,
- All the points say, (p,q) on the line PQ gives a solution of 2x+y = 6.
- All the solution of 2x+y = 6, lie on the line PQ.
- Points which are not the solution of 2x+y = 6 will not lie on the line PQ.

 ABCD CLASSES
ABCD CLASSES
