Equivalent versions of Euclid’s Fifth Postulate: Diagrams, Example
Equivalent versions of Euclid’s Fifth Postulate is very significant in the history of mathematics. We see that, by implication, no intersection of lines will occur when the sum of the measures of the interior angles on the same side of the falling line is exactly \({180^ \circ }\). There are several equivalent versions of this postulate. One of them is ‘Playfair’s Axiom’ (given by a Scottish mathematician John Playfair in \(1729)\), as stated below:
“For every line \(l\) and every point \(P\) not lying on \(l,\) there exists a unique line \(m\) passing through \(P\) and parallel to \( l.”\)
Of all the lines passing through the point \(P,\) only line \(m\) is parallel to line \(l,\) as shown in the diagram below.

What is the Equivalent Version?
Geometry has been taken from a variety of civilisations. Almost every significant civilisation has studied and used geometry in its prime. The Egyptian and the Indian civilisations were more focused on using geometry as a tool. Then Euclid came and changed the way people used to think of geometry. So instead of making it the tool, he thought of geometry as an abstract model of the world in which Euclid lived.
Five Basic Postulates of Euclidean Geometry
Below you can see Euclid’s five postulates:
Postulate 1: A straight line can be drawn from any point to any other point.
This postulate tells you that at least one straight line crosses two distinct points, but it does not say that there cannot be more than one line. However, without mentioning it, Euclid frequently assumed that there is a unique line connecting two distinct points in his work. You can state this result in the form of an axiom as follows:
Axiom: Given two distinct points, there is a unique line that passes through them.
How many lines passing through \(P\) also pass through \(Q\) on the given diagram. Only one, that is, the line \(PQ.\) How many lines passing through \(Q\) also pass through \(P?\) Only one, that is, the line \(PQ.\) Hence, the statement that is given above is self-evident, and it is considered as an axiom.
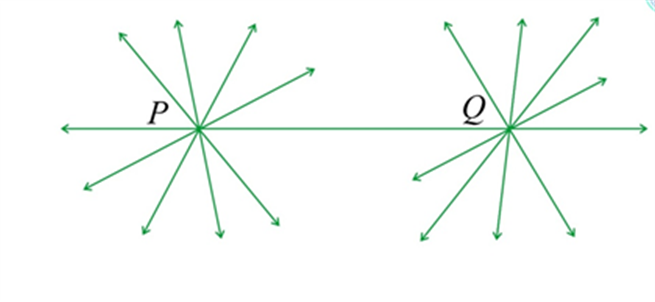
Postulate 2: A terminated line can be produced indefinitely.
Note that what you call the line segment nowadays is what Euclid called a terminated line. So, according to the present-day terms, the second postulate says that a line segment can be extended on either side to form a line in the given diagram.

Postulate 3: A circle can be drawn with any centre and radius.
Postulate 4: All the right angles are similar (equal) to one another.
Postulate 5: If the straight line that is falling on two straight lines makes the interior angles on the same side of it is taken together less than two right angles, then the two straight lines, if it is produced indefinitely, they meet on the side on which the sum of the angles is less than the two right angles.
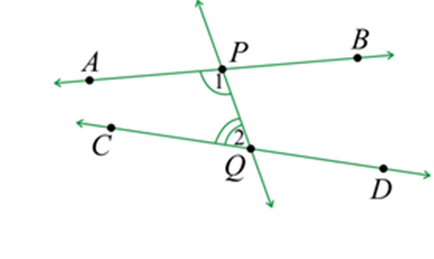
Example: The line \(PQ\) in the given diagram falls on lines \(AB\) and \(CD\) such that the sum of the interior angles \(1\) and \(2\) is less than \({180^ \circ }\) on the left side of \(PQ.\) Therefore, the lines \(AB\) and \(CD\) will eventually intersect on the left side of \(PQ.\)
Difference Between an Axiom and a Postulate
An axiom is a statement that is usually considered self-evident and assumed to be true without proof. It is used as the starting point in math proof for reducing other facts.
The axioms were considered different from the postulates. An axiom would mention a self-evident assumption common to many areas of the inquiry. In contrast, the postulate mentioned a hypothesis specific to a certain line of the inquiry that was approved without proof.
Example: In Euclid’s Elements, we can compare “common notions” (axioms) with the postulates.
There is generally no difference between what was classically referred to as the “axioms” and the “postulates” in modern mathematics. Modern mathematics distinguishes between the logical axioms and the non-logical axioms, with the latter sometimes referred to as the postulates.
What Does Euclid’s Fifth Postulate Imply?
Euclid’s fifth postulate states that if a straight line falling on two straight lines makes the interior angles on the same side of it taken together less than two right angles, then the two right angles, then both straight lines, if produced indefinitely, will meet on the other side on which the sum of angles is less than two right angles. First, you have to use this postulate and then prove it by using graphs and angles.
Complete step by step answer:
We know that Euclid’s fifth postulate states that if \(\angle 1 + \angle 2 < {180^ \circ },\), the line \(a\) and \(b\) meet on the right side of line \(c.\)
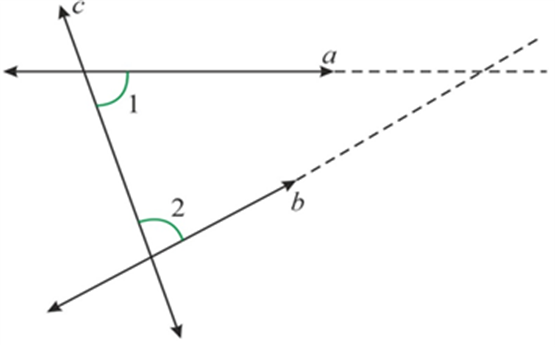
Now, since you know that \(a\) and \(b\) are parallel, then \(\angle 1 + \angle 2 = {180^ \circ }\), you get to see the below diagram:
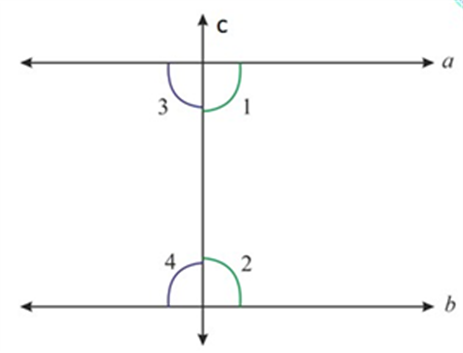
Hence, by Euclid’s fifth postulate, lines \(a\) and \(b\) will not meet on the right side of \(c\) as the sum is not less than \({180^ \circ }\)
In the same way, you can see \(\angle 3 + \angle 4 = {180^ \circ }\)
Therefore, by Euclid’s fifth postulate, lines \(a\) and \(b\) will not meet on the left side of \(c\) as the sum is not less than \({180^ \circ }\)
Thus, Euclid’s postulate implies the existence of parallel lines.
Solved Examples
Q.1. If \(A, B\) and \(C\) are three points on a line, and \(B\) lies between \(A\) and \(C\) in the given diagram, then prove that \(AB+BC=AC.\)

Ans: In the given diagram above, \(AC\) coincides with \(AB+BC\)
Also, Euclid’s Axiom \((4)\) says that things that coincide with one another are equal. So, it can be deduced that
\(AB+BC=AC\)
Note that in the given solution, it has been considered that there is a unique line that is passing through two points.
Q.2. Prove that an equilateral triangle may be constructed on any of the given line segments.
Ans: In the segment above, a line segment of any length is given, say AB in the given diagram.
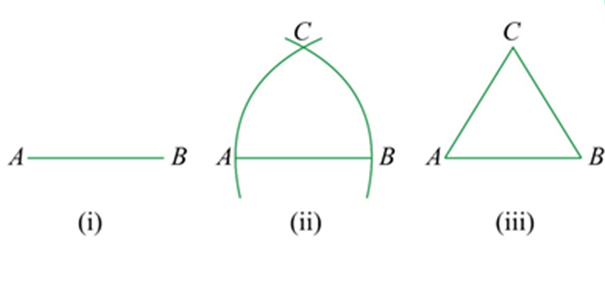
Here, you have to do some construction. Using Euclid’s postulate \(3,\) you can draw a circle with point \(A\) as the centre and \(AB\) as the radius in the given diagram. Similarly, you draw another circle with point \(B\) as the centre and \(BA\) as the radius. The two circles that meet at a point say \(C.\)
Now, draw the line segments \(AC\) and \(BC\) to form \(\Delta A B C\) in the given diagram.
So, you have to show that this triangle is the equilateral triangle, i.e., \(AB=AC=BC.\)
Now, \(AB=AC\), since they are the radii of the same circle (1)
Similarly, \(AB=BC\) (Radii of the same circle) (2)
From the given two facts, and Euclid’s axiom that things that are equal to the same thing are equal, you can conclude that \(AB=BC=AC\)
So, \(\Delta A B C\) is an equilateral triangle.
Q.3. Prove that the two lines that are both parallel to the same line are parallel to each other.
Ans: Three lines, \(l, m\) and \(n\) in a plane such that \(m||l\) and \(n||l.\)
Prove: \(m||n\)
If possible, let \(m\) be not parallel to \(n\). Then, \(m\) and \(n\) intersect in a unique point, say \(P.\)

Thus, through a point \(P\) outside \(l,\) two lines \(m\) and \(n,\) both parallel to \(l.\) This is a contradiction to the parallel axiom. So, the supposition is wrong.
Hence, \(m||n.\)
Q.4. Prove that two distinct lines cannot have more than one point in common.
Ans: Here, we are given two lines \(l\) and \(m.\) You need to prove that they have only a single point in common. Let us assume that the two lines intersect in two distinct points, say \(P\) and \(Q.\) So, you have two lines that are passing through two distinct points \(P\) and \(Q.\)
But this assumption clashes with the axiom that only one line can pass through two distinct points. So, the assumption that we started with that two lines can pass through two distinct points is wrong.
From this, we understand that we are forced to conclude that two distinct lines cannot have more than one point in common.
Q.5. Prove that if lines \(AB, AC, AD\) and \(AE\) are parallel to line \(l,\) then points \(A, B, C, D\) and \(E\) are collinear.
Ans: Lines \(AB, AC, AD\) and \(AE\) are parallel to a line \(l.\)
Prove: \(A,B,C, D\) and \(E\) are collinear.
Since lines \(AB, AC, AD\) and \(AE\) are parallel to a line \(l.\)
Therefore, point \(A\) lies outside \(l\) and through \(A\) lines \(AB, AC, AD\) and \(AE\) are drawn parallel to \(l.\) But, by parallel axiom, only one line can be drawn parallel to \(l, \) through a point outside it.
Therefore, the points \(A, B, C, D, E\) lie on the same line.
Hence, points \(A, B, C, D\) and \(E\) are collinear points.
Q.1. What is the equivalent version?
Ans: Geometry has taken from a variety of civilisations. Almost every significant civilisation has studied and used geometry in its prime. The Egyptian and the Indian civilisations were more focused on using geometry as a tool. Then Euclid came and changed the way people use to think in geometry. So instead of making it the tool, he thought of geometry as an abstract model of the world in which Euclid lived.
Q.2. Which of the five postulates is equivalent to Playfair’s postulate?
Ans: The definition of the fifth postulate is taken so that the parallel lines are the lines that do not intersect or have some line that is intersecting them in the same angles. Playfair’s axiom is contextually equivalent to Euclid’s fifth postulate and is thus logically independent of the first four postulates.
Q.3. How would you rewrite Euclid’s fifth postulate?
Ans: This postulate can be rewritten in reference to the given below diagram: You can consider a straight line \(PQ\) that falls on both straight lines \(AB\) and \(CD\) in such a way that the total sum of the interior angles \(\angle 1\) and \(\angle 2\) is less than \(180\) degrees on the left side of the straight line \(PQ.\) In this case, \(AB\) and \(CD,\) if produced, will meet at the left side of \(PQ.\)
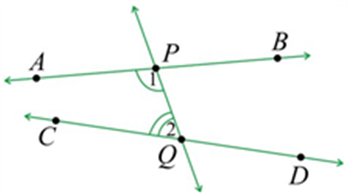
Q 4. Who proved Euclid’s fifth postulate?
Ans: The Persian mathematician, astronomer, philosopher, and poet Omar Khayyam \((1050-1153)\) attempted to prove the fifth postulate.
Q.5. What is the equivalent of the fifth postulate?
Ans: If the straight line that is falling on two straight lines makes the interior angles on the same side of it is taken together less than two right angles, then the two straight lines, if it is produced indefinitely, they meet on the side on which the sum of the angles is less than the two right angles.

 ABCD CLASSES
ABCD CLASSES
