Irrational Numbers
- Books Name
- ABCD CLASSES Mathematics Book
- Publication
- ABCD CLASSES
- Course
- CBSE Class 9
- Subject
- Mathmatics
Irrational Numbers
An irrational number cannot be expressed as a ratio between two numbers and it cannot be written as a simple fraction because there is not a finite number of numbers when written as a decimal. Instead, the numbers in the decimal would go on forever, without repeating.
Common Examples of Irrational Numbers
- Pi, which begins with 3.14, is one of the most common irrational numbers. Pi is determined by calculating the ratio of the circumference of a circle (the distance around the circle) to the diameter of that same circle (the distance across the circle). Pi has been calculated to over a quadrillion decimal places, but no pattern has ever been found; therefore it is an irrational number.
- e, also known as Euler's number, is another common irrational number. The number is named for Leonard Euler, who first introduced e in 1731 in a letter he wrote; however, he had started using the number in 1727 or 1728. e is a universal number. The beginning of this number written out is 2.71828. e is the limit of (1 + 1/n)n as n approaches infinity. This expression is part of the discussion surrounding the subject of compound interest.
- The Square Root of 2, written as √2, is also an irrational number. The first part of this number would be written as 1.41421356237…but the numbers go on into infinity and do not ever repeat, and they do not ever terminate. A square root is an opposite of squaring a number, meaning that the square root of two times the square root of two equals two. This means that 1.41421356237… multiplied by 1.41421356237… equals two, but it is difficult to be exact in showing this because the square root of two does not end, so when you actually do the multiplication, the resulting number will be close to two, but will not actually be two exactly. Because the square root of two never repeats and never ends, it is an irrational number. Many other square roots and cubed roots are irrational numbers; however, not all square roots are.
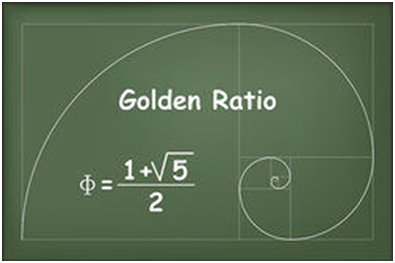
The Golden Ratio, written as a symbol, is an irrational number that begins with 1.61803398874989484820...
Irrational Numbers
Chapter - 1 - Number System
Examples of Irrational Numbers
An irrational number cannot be expressed as a ratio between two numbers and it cannot be written as a simple fraction because there is not a finite number of numbers when written as a decimal. Instead, the numbers in the decimal would go on forever, without repeating.
Advertisement
Common Examples of Irrational Numbers
- Pi, which begins with 3.14, is one of the most common irrational numbers. Pi is determined by calculating the ratio of the circumference of a circle (the distance around the circle) to the diameter of that same circle (the distance across the circle). Pi has been calculated to over a quadrillion decimal places, but no pattern has ever been found; therefore it is an irrational number.
- e, also known as Euler's number, is another common irrational number. The number is named for Leonard Euler, who first introduced e in 1731 in a letter he wrote; however, he had started using the number in 1727 or 1728. e is a universal number. The beginning of this number written out is 2.71828. e is the limit of (1 + 1/n)n as n approaches infinity. This expression is part of the discussion surrounding the subject of compound interest.
- The Square Root of 2, written as √2, is also an irrational number. The first part of this number would be written as 1.41421356237…but the numbers go on into infinity and do not ever repeat, and they do not ever terminate. A square root is the opposite of squaring a number, meaning that the square root of two times the square root of two equals two. This means that 1.41421356237… multiplied by 1.41421356237… equals two, but it is difficult to be exact in showing this because the square root of two does not end, so when you actually do the multiplication, the resulting number will be close to two, but will not actually be two exactly. Because the square root of two never repeats and never ends, it is an irrational number. Many other square roots and cubed roots are irrational numbers; however, not all square roots are.
The Golden Ratio, written as a symbol, is an irrational number that begins with 1.61803398874989484820...
Real Numbers and their Decimal Expansions
- Books Name
- ABCD CLASSES Mathematics Book
- Publication
- ABCD CLASSES
- Course
- CBSE Class 9
- Subject
- Mathmatics
Real Numbers and Their Decimal Expansions
In Mathematics, a real number is a combination of rational numbers and irrational numbers. Rational and irrational numbers can be expressed in their decimal form. The real numbers can be represented using the number line. If the numbers cannot be expressed on the number line, then the numbers are called imaginary numbers. In this article, we are going to learn the real numbers and their decimal expansions in detail.
Decimal Expansion of Real Numbers
We know that the combination of rational and irrational numbers is called real numbers. Now, we will have a look at the decimal expansion of rational and irrational numbers. The decimal expansion of real numbers can be classified into three types. They are:
- Terminating Decimals
- Non-terminating and Repeating Decimals
- Non-terminating and Non-repeating Decimals
Terminating Decimals
The decimal expansion terminates or ends after finite numbers of steps. Such types of decimal expansion are called terminating decimals. It means that, after the decimal point, the numbers come to an end at a certain point.
For example, ½ is a rational number and its decimal expansion is 0.5.
Note: Terminating decimals are rational numbers.
Non-terminating and Repeating Decimals
In non-terminating decimals, the decimal expansion does not come to an end and it has an infinite number of digits. The repeating decimals are the decimals, where a certain number of digits uniformly repeats after the decimal point.
An example of non-terminating and repeating decimals is 1.454545…Here, the digit 45 constantly repeats after the decimal point.
Note: Non-terminating and repeating decimals are rational numbers.
Non-terminating and Non-repeating Decimals
Non-terminating and non-repeating decimals are the types of decimal expansion, in which the number after the decimal point is non-terminating and the decimal numbers are not repeating.
An example of a non-terminating and non-terminating decimal is 2.34765….. Here, the numbers after the decimal point are infinite and they are not repeating.
Note: Non-terminating and non-repeating numbers are irrational numbers.
Examples
Go through the following examples to understand the concept of real numbers and their decimal expansion.
Example 1:
Prove that 3.1426 is a rational number.
Solution:
To prove: 3.1426 is a rational number.
The number 3.1426 can be written as 31426/10000
31426/10000 = 3.1426
Hence, the number 3.1426 can be expressed in the form of 31426/10000, which is equal to p/q, where q≠ 0.
Hence, proved.
Example 2:
Show that the decimal expansion of 14/11 is non-terminating and repeating.
Solution:
Given number: 14/11
The decimal expansion of 14/11 is 1.2727272727…
Here, the number 27 after the decimal point is repeating and the number 1.2727272727…is non-terminating.
Since the given number 14/11 is non-terminating and repeating, we can say that 14/11 is a rational number.
Hence, proved.
Also, read Operations on Real Numbers.
Practice Problems
Solve the following problems:
- Prove that 0.2353535 is a rational number.
- Convert the following real numbers in their decimal expansion:
- 1/11
- 329/400
- 3/13
- Classify the following numbers as rational or irrational numbers:
- √225
- 7.478478…
Real Numbers and their Decimal Expansions
Real Numbers and Their Decimal Expansions
In Mathematics, a real number is a combination of rational numbers and irrational numbers. The rational and irrational numbers can be expressed in their decimal form. The real numbers can be represented using the number line. If the numbers cannot be expressed on the number line, then the numbers are called imaginary numbers. In this article, we are going to learn the real numbers and their decimal expansions in detail.
Decimal Expansion of Real Numbers
We know that the combination of rational and irrational numbers is called real numbers. Now, we will have a look at the decimal expansion of rational and irrational numbers. The decimal expansion of real numbers can be classified into three types. They are:
- Terminating Decimals
- Non-terminating and Repeating Decimals
- Non-terminating and Non-repeating Decimals
Terminating Decimals
The decimal expansion terminates or ends after finite numbers of steps. Such types of decimal expansion are called terminating decimals. It means that, after the decimal point, the numbers come to an end at a certain point.
For example, ½ is a rational number and its decimal expansion is 0.5.
Note: Terminating decimals are rational numbers.
Non-terminating and Repeating Decimals
In non-terminating decimals, the decimal expansion does not come to an end and it has an infinite number of digits. The repeating decimals are the decimals, where a certain number of digits uniformly repeats after the decimal point.
An example of non-terminating and repeating decimals is 1.454545…Here, the digit 45 constantly repeats after the decimal point.
Note: Non-terminating and repeating decimals are rational numbers.
Non-terminating and Non-repeating Decimals
Non-terminating and non-repeating decimals are one of the types of decimal expansion, in which the number after the decimal point is non-terminating and the decimal numbers are not repeating.
An example of non-terminating and non-terminating decimal is 2.34765….. Here, the numbers after the decimal point are infinite and they are not repeating.
Note: Non-terminating and non-repeating numbers are irrational numbers.
Examples
Go through the following examples to understand the concept of real numbers and their decimal expansion.
Example 1:
Prove that 3.1426 is a rational number.
Solution:
To prove: 3.1426 is a rational number.
The number 3.1426 can be written as 31426/10000
31426/10000 = 3.1426
Hence, the number 3.1426 can be expressed in the form of 31426/10000, which is equal to p/q, where q≠ 0.
Hence, proved.
Example 2:
Show that the decimal expansion of 14/11 is non-terminating and repeating.
Solution:
Given number: 14/11
The decimal expansion of 14/11 is 1.2727272727…
Here, the number 27 after the decimal point is repeating and the number 1.2727272727…is non-terminating.
Since the given number 14/11 is non-terminating and repeating, we can say that 14/11 is a rational number.
Hence, proved.
Also, read: Operations on Real Numbers.
Practice Problems
Solve the following problems:
- Prove that 0.2353535 is a rational number.
- Convert the following real numbers in their decimal expansion:
- 1/11
- 329/400
- 3/13
- Classify the following numbers as rational or irrational numbers:
- √225
- 7.478478…
Representing Real Number on the Number Line
- Books Name
- ABCD CLASSES Mathematics Book
- Publication
- ABCD CLASSES
- Course
- CBSE Class 9
- Subject
- Mathmatics
Representing Real Numbers on the Number Line
In Mathematics, a number line is a straight line, which represents the integers in equal intervals. The number line extends infinitely in both directions, and it contains both positive and negative integers. In this article, we are going to learn how to represent the real numbers on the number line with a complete explanation.
Real Number Line
The real number is defined as the union of a set of rational numbers and a set of irrational numbers. The real numbers include natural numbers, whole numbers, integers, rational and irrational numbers. We can represent all these types of numbers in the number line. The complex number is not represented using the number line as it is not included in the real number system.
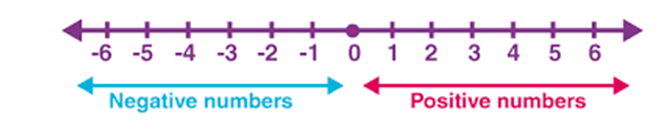
The Real number line is just a number line. The point associated with the real number line is called the coordinate. The number “0” represents the origin. All the positive numbers are represented on the right side of the origin, whereas all the negative numbers are represented on the left side of the origin.
How to Represent the Real Numbers on the Number Line
Go through the following steps to represent the real numbers on the number line.
Step 1: Draw a horizontal line with arrows on both sides. Mark the origin “0” anywhere on the horizontal line.
Step 2: Mark the real numbers on the number line of equal lengths on both sides with a definite scale.
Step 3: Mark the positive numbers on the right side of the origin and negative numbers on the left side of the origin.
Step 4: If the given point is large, adjust the scale accordingly.
Step 5: If the given number is a rational or irrational number, convert them into a decimal format and mark the points using the process of successive magnification.
Note: The process of visualization of numbers on the number line using the magnifying glass is called the process of successive magnification.
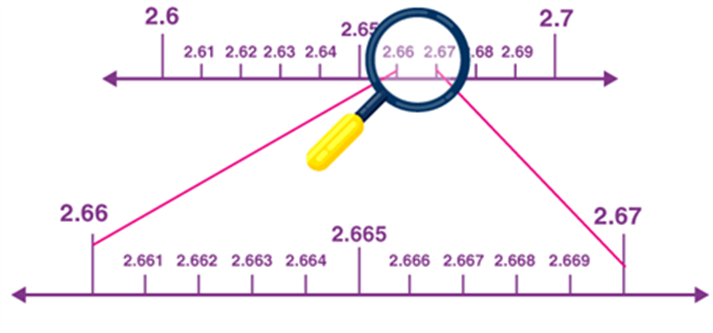
Assume that, we want to locate the point 2.665 on the number line.
We know that point 2.665 lies on the number line between 2 and 3.
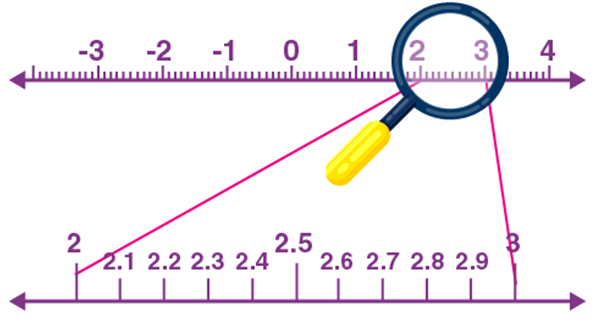
In between 2 and 3, there are 10 equal parts, say 2.1, 2,2, 2.3, and so on. In order to locate the 2.665 exactly, again focus on the points between 2.6 and 2.7, as 2.665 is located in between.
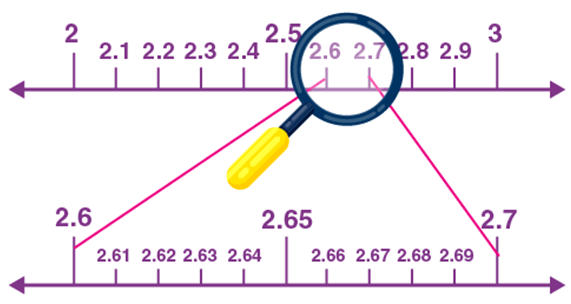
Since 2.665 is located between 2.66 and 2.67, again focus on these points.
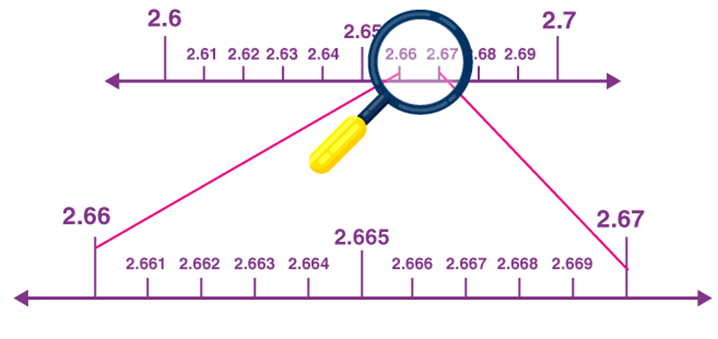
Thus, point 2.665 is located on the number line using the process of successive magnification. So, with the help of this method, one can locate the point by a sufficient successive magnification process to visualize the representation of real numbers (rational and irrational numbers) on the number line.
Also, read Rational and Irrational Numbers.
Practice Problems
Plot the following real numbers on the number line:
- 2.5
- 2.67
- 5.37
- 3.765
- 4.55
Representing Real Number on the Number Line
Representing Real Numbers on the Number Line
In Mathematics, a number line is a straight line, which represents the integers in equal intervals. The number line extends infinitely in both directions, and it contains both positive and negative integers. In this article, we are going to learn how to represent the real numbers on the number line with a complete explanation.
Real Number Line
The real number is defined as the union of a set of rational numbers and the set of irrational numbers. The real numbers include natural numbers, whole numbers, integer, rational and irrational numbers. We can represent all these types of numbers in the number line. The complex number is not represented using the number line as it is not included in the real number system.

The Real number line is just a number line. The point associated with the real number line is called the coordinate. The number “0” represents the origin. All the positive numbers are represented on the right side of the origin, whereas all the negative numbers are represented on the left side of the origin.
How to Represent the Real Numbers on the Number Line
Go through the following steps to represent the real numbers on the number line.
Step 1: Draw a horizontal line with arrows on both sides. Mark the origin “0” anywhere on the horizontal line.
Step 2: Mark the real numbers on the number line of equal lengths on both sides with a definite scale.
Step 3: Mark the positive numbers on the right side of the origin and negative numbers on the left side of the origin.
Step 4: If the given point is large, adjust the scale accordingly.
Step 5: If the given number is a rational or irrational number, convert them into a decimal format and mark the points using the process of successive magnification.
Note: The process of visualization of numbers on the number line using the magnifying glass is called the process of successive magnification.
Assume that, we want to locate the point 2.665 on the number line.
We know that point 2.665 lies on the number line between 2 and 3.
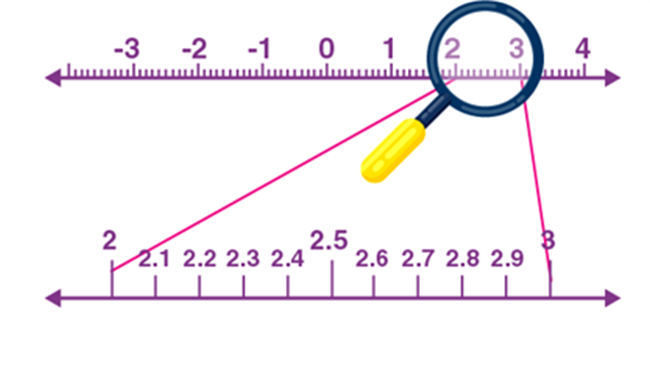
In between 2 and 3, there are 10 equal parts, say 2.1, 2,2, 2.3, and so on. In order to locate the 2.665 exactly, again focus on the points between 2.6 and 2.7, as 2.665 is located in between.
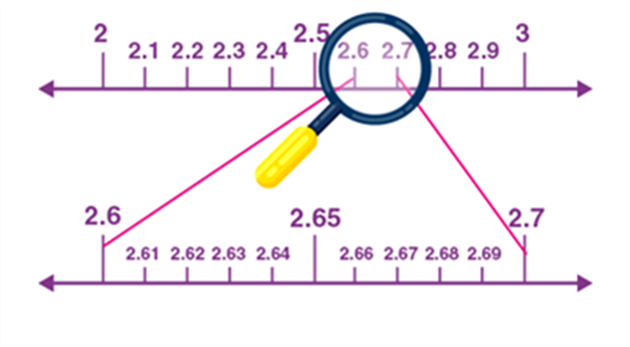
Since 2.665 is located between 2.66 and 2.67, again focus on these points.
Thus, point 2.665 is located on the number line using the process of successive magnification. So, with the help of this method, one can locate the point by a sufficient successive magnification process to visualize the representation of real numbers (rational and irrational numbers) on the number line.
Also, read: Rational and Irrational Numbers.
Practice Problems
Plot the following real numbers on the number line:
- 2.5
- 2.67
- 5.37
- 3.765
- 4.55
To learn more Maths-related and class-wise concepts, visit – The Learning App and learn the concepts easily by exploring more videos.
Operations on Real Numbers
- Books Name
- ABCD CLASSES Mathematics Book
- Publication
- ABCD CLASSES
- Course
- CBSE Class 9
- Subject
- Mathmatics
Operations on Real Numbers
Real numbers are those numbers that are a combination of rational numbers and irrational numbers in the number system of maths. All the arithmetic operations like addition, subtraction, multiplication, etc. can be performed on these numbers. Besides imaginary numbers are not real numbers. Imaginary numbers are used for defining complex numbers. To get real numbers, first, we have to understand rational numbers and irrational numbers. Rational numbers are those numbers that can be written as p/q where p is numerator and q is dominator and p and q are integers. For example, 5 can be written as 5/1so it is a rational number and irrational numbers are those numbers that cannot be written in form of p/q.
For example √3 is irrational numbers, it can be written as 1.73205081 and continuous to infinity, and it cannot be written in form of fraction and is non-terminating form and non-recurring decimals. And if combine rational numbers and irrational numbers it became real numbers.
Example: 12, -8, 5.60, 5/1, π(3.14) etc.
Real numbers can be positive and negative, and it is denoted by R. All the decimals, natural numbers and fraction come under this category.
Operations on Real Numbers
The four basics mathematical operations addition, division, multiplication, and subtraction. Now we will understand these operations on both rational and irrational numbers.
Operation on Two Rational Numbers
When we perform arithmetic operations on two rational numbers like addition, subtraction, division, and multiplication then the result will be rational numbers.
Example:
0.25 + 0.25 = 0.50 can be written as 50/100 which is form of p/q.
0.20 – 0.10 = 0.10 can be written as 10/100 which is form of p/q.
0.4 multiplied by 184 is 73.6 and can be written as 736/10.
0.252 divided by 0.4 is 0.63 and can be written as 63/100.
Operations on Two Irrational Numbers
When we perform arithmetic operations like addition, subtraction, multiplication, or division on two irrational numbers then the result can be rational numbers or irrational numbers.
Example:
√2 + √3 = 3.14 can be written as 314/100 which is rational number.
√3 – √3 = 0 or 5√4 – 4√3 = 3.07 which can be written as 307/100 which is rational number.
When √5 is multiplied to √5, we get 5 which is rational number or when √3 is multiplied to √5, we get √15 which is irrational number. When √8 is divided by √8 we get 8 which is rational number or if √5 is divided by √3 then we get (√5)/(√3) which is irrational number.
Operation on a rational number and an irrational number
Addition
When we add an irrational number and a rational number then the result will be an irrational number. When 3 is added to 2√5 then the result will be an irrational number.
Subtraction
When we perform subtraction on an irrational number and a rational number then the result will be an irrational number. When 5√6 is subtracted to 3 then the result will be an irrational number.
Multiplication
When we perform this operation the result can be irrational or rational. When 3 is multiplied to √5 then the result will be 3√5 which is an irrational number and if √12 is multiplied to √3 then the result will be √36 and it can be written as 6 which is a rational number.
Division
A rational number is divided by an irrational number or vice versa then the result will be always an irrational number. When 4 is divided by √2 then results will be 4√2 which is an irrational number.
Properties of Real Numbers
We have four properties which are commutative property, associative property, distributive property, and identity property. Consider a, b and c are three real numbers. Then these properties can be described as
Commutative Property
If a and b are the numbers, then a + b = b + a for addition and a × b = b × a for multiplication.
Addition:
a + b = b + a;
5 + 6 = 6 + 5
Multiplication:
a × b = b × a;
4 × 2 = 2 × 4
Associative Property
If a, b and c are the real numbers then the form will be
a + (b + c) = (a + b) = c for addition and (a.b)c = a(b.c) for multiplication
Addition:
a + (b + c) = (a + b) = c ;
5 + (3 + 2) = (5 + 3) + 2
Multiplication:
(a.b)c = a(b.c) ;
(4×2)×6 = 4×(2×6)
Distributive Property
If a, b and c are the real numbers then the final form will be
a (b + c) = ab + ac and (a + b) c = ac + ab
5 (2+3)=5×2+5×3 the answer will be 25 for both left and right term.
Identity Property
Addition: a + 0 = 0 (0 is the additive identity)
Multiplication: a×1=1×a=1 (1 is multiplicative identity)
Real Numbers
Rational numbers: 4/5, 0.82
Integer numbers: {… – 3, -2, -1,0,1,2,3…}
Whole numbers: {0,1,2,3…}
Natural numbers: {1,2,3…}
Irrational numbers: √2, π, 0.102012…
Operations on Real Numbers
Operations on Real Numbers
Real numbers are those numbers that are a combination of rational numbers and irrational numbers in the number system of maths. All the arithmetic operations like addition, subtraction, multiplication, etc. can be performed on these numbers. Besides imaginary numbers are not real numbers. Imaginary numbers are used for defining complex numbers. To get real numbers, first, we have to understand rational numbers and irrational numbers. Rational numbers are those numbers that can be written as p/q where p is numerator and q is dominator and p and q are integers. For example, 5 can be written as 5/1so it is a rational number and irrational numbers are those numbers that cannot be written in form of p/q.
For example √3 is irrational numbers, it can be written as 1.73205081 and continuous to infinity, and it cannot be written in form of fraction and is non-terminating form and non-recurring decimals. And if combine rational numbers and irrational numbers it became real numbers.
Example: 12, -8, 5.60, 5/1, π(3.14) etc.
Real numbers can be positive and negative, and it is denoted by R. All the decimals, natural numbers and fraction come under this category.
Operations on Real Numbers
The four basics mathematical operations addition, division, multiplication, and subtraction. Now we will understand these operations on both rational and irrational numbers.
Operation on Two Rational Numbers
When we perform arithmetic operations on two rational numbers like addition, subtraction, division, and multiplication then the result will be rational numbers.
Example:
0.25 + 0.25 = 0.50 can be written as 50/100 which is form of p/q.
0.20 – 0.10 = 0.10 can be written as 10/100 which is form of p/q.
0.4 multiplied by 184 is 73.6 and can be written as 736/10.
0.252 divided by 0.4 is 0.63 and can be written as 63/100.
Operations on Two Irrational Numbers
When we perform arithmetic operations like addition, subtraction, multiplication, or division on two irrational numbers then the result can be rational numbers or irrational numbers.
Example:
√2 + √3 = 3.14 can be written as 314/100 which is rational number.
√3 – √3 = 0 or 5√4 – 4√3 = 3.07 which can be written as 307/100 which is rational number.
When √5 is multiplied to √5, we get 5 which is rational number or when √3 is multiplied to √5, we get √15 which is irrational number. When √8 is divided by √8 we get 8 which is rational number or if √5 is divided by √3 then we get (√5)/(√3) which is irrational number.
Operation on a rational number and an irrational number
Addition
When we add an irrational number and a rational number then the result will be an irrational number. When 3 is added to 2√5 then the result will be an irrational number.
Subtraction
When we perform subtraction on an irrational number and a rational number then the result will be an irrational number. When 5√6 is subtracted to 3 then the result will be an irrational number.
Multiplication
When we perform this operation the result can be irrational or rational. When 3 is multiplied to √5 then the result will be 3√5 which is an irrational number and if √12 is multiplied to √3 then the result will be √36 and it can be written as 6 which is a rational number.
Division
A rational number is divided by an irrational number or vice versa then the result will be always an irrational number. When 4 is divided by √2 then results will be 4√2 which is an irrational number.
Properties of Real Numbers
We have four properties which are commutative property, associative property, distributive property, and identity property. Consider a, b and c are three real numbers. Then these properties can be described as
Commutative Property
If a and b are the numbers, then a + b = b + a for addition and a × b = b × a for multiplication.
Addition:
a + b = b + a;
5 + 6 = 6 + 5
Multiplication:
a × b = b × a;
4 × 2 = 2 × 4
Associative Property
If a, b and c are the real numbers then the form will be
a + (b + c) = (a + b) = c for addition and (a.b)c = a(b.c) for multiplication
Addition:
a + (b + c) = (a + b) = c ;
5 + (3 + 2) = (5 + 3) + 2
Multiplication:
(a.b)c = a(b.c) ;
(4×2)×6 = 4×(2×6)
Distributive Property
If a, b and c are the real numbers then the final form will be
a (b + c) = ab + ac and (a + b) c = ac + ab
5 (2+3)=5×2+5×3 the answer will be 25 for both left and right term.
Identity Property
Addition: a + 0 = 0 (0 is the additive identity)
Multiplication: a×1=1×a=1 (1 is multiplicative identity)
Real Numbers
Rational numbers: 4/5, 0.82
Integer numbers: {… – 3, -2, -1,0,1,2,3…}
Whole numbers: {0,1,2,3…}
Natural numbers: {1,2,3…}
Irrational numbers: √2, π, 0.102012…
Laws of Exponents for Real Number
- Books Name
- ABCD CLASSES Mathematics Book
- Publication
- ABCD CLASSES
- Course
- CBSE Class 9
- Subject
- Mathmatics
Laws of Exponents or Exponent Rules
What is meant by an exponent? You must have come across the expression 3². Here 3 is the base and 2 is the exponent. Exponents are also called Powers or Indices. The exponent of a number tells how many times to use the number in a multiplication. Let us study the laws of an exponent. It is very important to understand how the laws of exponents laws are formulated.

1. Product law
According to the product law of exponents when multiplying two numbers that have the same base then we can add the exponents
am × an= a m+n
where a, m and n all are natural numbers. Here the base should be the same in both the quantities. For example,
- 2³ × 24 = 27
- 22/3 × 21/5 = 2 2/3 + 1/5 = 2(10+3)/15 . We get, = 212/15
- (-6) 3 x (-6) 2 = (-6) 3+2 = (-6) 5
2. Quotient Law
According to the quotient law of exponents, we can divide two numbers with the same base by subtracting the exponents. In order to divide two exponents that have the same base, subtract the power in the denominator from the power in the numerator.
am ÷ an = a m-n
where a, m and n all are natural numbers. Here the base should be the same in both the quantities. For example,
- 25 ÷ 23 = 2²
- p6 ÷ p2 = p 6 – 2 = p 4
3. Power Law
According to the power law of exponents if a number raise a power to a power, just multiply the exponents
(am)n = am×n
Here there is one base a and two powers m and n. For example, ( 53 )2 = 53×2 = 56
Important Points to Remember on Exponent Rules
- 1an = a-n. A non zero base raised to a negative exponent is equal to the reciprocal of the base raised to the positive exponent or 1a−n = a+n
- a0 = 1. This says that anything raised to the zero power is 1. For example, 50= 1, (1000) 0 = 1
- a1 = a
Power of Product
The power of product rule states that: (ab)m = am × bm, a and b are positive real numbers and m is the rational number. For example, ( 2 × 5)10 = 210 × 510
Power of Quotient
The power of product rule states that:
ab^n = anbn
Or, 25^12 = 212512
Laws of Exponents for Real Number
Laws of Exponents or Exponent Rules
What is meant by an exponent? You must have come across the expression 3². Here 3 is the base and 2 is the exponent. Exponents are also called Powers or Indices. The exponent of a number tells how many times to use the number in a multiplication. Let us study the laws of exponent. It is very important to understand how the laws of exponents laws are formulated.

(Source: math warehouse)
1. Product law
According to the product law of exponents when multiplying two numbers that have the same base then we can add the exponents
am × an= a m+n
where a, m and n all are natural numbers. Here the base should be the same in both the quantities. For example,
- 2³ × 24 = 27
- 22/3 × 21/5 = 2 2/3 + 1/5 = 2(10+3)/15 . We get, = 212/15
- (-6) 3 x (-6) 2 = (-6) 3+2 = (-6) 5
2. Quotient Law
According to the quotient law of exponents, we can divide two numbers with the same base by subtracting the exponents. In order to divide two exponents that have the same base, subtract the power in the denominator from the power in the numerator.
am ÷ an = a m-n
where a, m and n all are natural numbers. Here the base should be the same in both the quantities. For example,
- 25 ÷ 23 = 2²
- p6 ÷ p2 = p 6 – 2 = p 4
3. Power Law
According to the power law of exponents if a number raise a power to a power, just multiply the exponents
(am)n = am×n
Here there is one base a and two powers m and n. For example, ( 53 )2 = 53×2 = 56
Important Points to Remember on Exponent Rules
- 1an = a-n. A non zero base raised to a negative exponent is equal to the reciprocal of the base raised to the positive exponent or 1a−n = a+n
- a0 = 1. This says that anything raised to the zero power is 1. For example, 50= 1, (1000) 0 = 1
- a1 = a
Power of Product
The power of product rule states that: (ab)m = am × bm, a and b are positive real numbers and m is the rational number. For example, ( 2 × 5)10 = 210 × 510
Power of Quotient
The power of product rule states that:
ab^n = anbn
Or, 25^12 = 212512
Solved Questions on Exponent Rules
Question 1: If 125 = 3t × 4t calculate the value of t.
- 2.5
- 5
- 10
- 20
- 40
Answer : The correct option is “B”. Given: 125 = 3t × 4t. If two terms have the same power and they are multiplied then the power can be taken as common = 125 =( 3 × 4 )t = 125 = 12t. If two terms have the same base, then we can equate their powers.
Question 2: Which of the following expresses the power law of exponents?
- am × an= a m+n
- am × bn= (ab) m
- a0 = 1
- (am )n= a mn
Answer : The correct answer is “D”. The power law states that to raise a power to a power, just multiply the exponents. Therefore, (am)n= a m×n = amn. So, D is the correct option.
Question 3: What is difference between power and exponent?
Answer: We often call exponents powers or indices. Power refers to an expression which is representing repeated multiplications of the same number. While exponent is the quantity which is representing the power to which we raise the number. We use both these terms interchangeably in math.
Question 4: What is the zero exponent rule?
Answer: When there is a number or variable that is raise to a power, the number (or variable) is referred to as the base whereas the superscript number refers to the exponent or power. Thus, the zero exponent rule states that any base having an exponent of zero equals to one.
Question 5: What are the three laws of exponent?
Answer: The three laws of exponent are firstly, multiplication of identical bases and addition of exponents. Secondly, dividing the identical bases and subtracting the exponent. Thirdly, multiplication of exponent when two or more exponents and just one base is present.
Question 6: What is exponential form?
Answer: Exponential form refers to a numeric form that involves exponents. One method to write such a number is by identifying that each position is representing a power (exponent) of 10. Thus, you can initially break it up into different pieces

 ABCD CLASSES
ABCD CLASSES
