Area of a Triangle- By Heron's formula
- Books Name
- ABCD CLASSES Mathematics Book
- Publication
- ABCD CLASSES
- Course
- CBSE Class 9
- Subject
- Mathmatics
Heron's Formula
Heron’s formula is used to find the area of a triangle when we know the length of all its sides. It is also termed Hero’s Formula. We can Heron’s formula to find different types of triangles, such as scalene, isosceles and equilateral triangles. We don’t have to need to know the angle measurement of a triangle to calculate its area, by using Heron’s formula.
What is Heron’s Formula?
Heron’s formula is a formula to calculate the area of triangles, given the three sides of the triangle. This formula is also used to find the area of the quadrilateral, by dividing the quadrilateral into two triangles, along its diagonal.
If a, b and c are the three sides of a triangle, respectively, then Heron’s formula is given by:
|
Semiperimeter, s= Perimeter of triangle/2 = (a+b+c)/2 |
History of Heron’s Formula
Hero of Alexandria was a great mathematician who derived the formula for the calculation of the area of a triangle using the length of all three sides. He also extended this idea to find the area of quadrilateral and also higher-order polygons. This formula has its huge applications in trigonometry such as proving the law of cosines or the law of cotangents, etc.
Heron’s Formula for Triangles
According to Heron, we can find the area of any given triangle, whether it is a scalene, isosceles or equilateral, by using the formula, provided by the sides of the triangle.
Suppose, a triangle ABC, whose sides are a, b and c, respectively. Thus, the area of a triangle can be given by;
Where “s” is semi-perimeter = (a+b+c) / 2
And a, b, c are the three sides of the triangle.
Proof of Heron’s Formula
There are two methods by which we can derive Heron’s formula.
- First, by using trigonometric identities and cosine rule.
- Secondly, solving algebraic expressions using the Pythagoras theorem.
Let us see one by one both the proofs and derivation.
Using Cosine Rule
Let us prove the result using the law of cosines:
Let a, b, and c be the sides of the triangle and α, β, and γ are opposite angles to the sides.
We know that the law of cosines is
Again, using trig identity, we have
=
Here, Base of triangle = a
Altitude = b sinγ
Now,

Using Pythagoras Theorem
Area of a Triangle with 3 Sides
Area of ∆ABC is given by
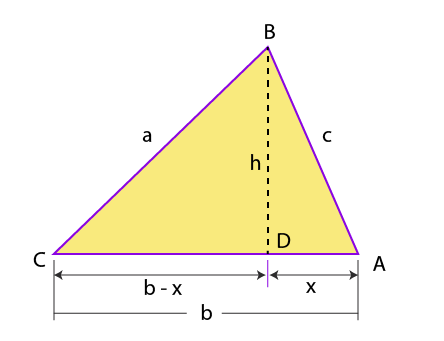
A = 1/2 bh _ _ _ _ (i)
Draw a perpendicular BD on AC
Consider a ∆ADB
x2 + h2 = c2
x2 = c2 − h2—(ii)
⇒x = √(c2−h2)−−−−−−—(iii)
Consider a ∆CDB,
(b−x)2 + h2 = a2
(b−x)2 = a2 − h2
b2 − 2bx + x2 = a2–h2
Substituting the value of x and x2 from equation (ii) and (iii), we get
b2 – 2b√(c2−h2)+ c2−h2 = a2 − h2
b2 + c2 − a2 = 2b√(c2 − h2)
Squaring on both sides, we get;
(b2+c2–a2)2 = 4b2(c2−h2)
The perimeter of a ∆ABC is
P= a+b+c
Substituting the value of h in equation (i), we get;
Semi perimeter(s) =
Note: Heron’s formula is applicable to all types of triangles and the formula can also be derived using the law of cosines and the law of Cotangents.
How to Find the Area Using Heron’s Formula?
To find the area of a triangle using Heron’s formula, we have to follow two steps:
- Find the perimeter of the given triangle
- Then, find the value of the semi-perimeter of the given triangle; S = (a+b+c)/2
- Now use Heron’s formula to find the area of a triangle (√(s(s – a)(s – b)(s – c)))
- Finally, represent the area with the accurate square units (such as m2, cm2, in2, etc.)
Heron’s Formula for Equilateral Triangle
As we know the equilateral triangle has all its sides equal. To find the area of the equilateral triangle let us first find the semi perimeter of the equilateral triangle will be:
s = (a+a+a)/2
s=3a/2
where a is the length of the side.
Now, as per the heron’s formula, we know;
Since, a = b = c
Therefore,
A = √[s(s-a)3]
which is the required formula.
Heron’s Formula for Isosceles Triangle
An isosceles triangle has two of its sides equal and the angles corresponding to these sides are congruent. To find the area of an isosceles triangle, we can derive the heron’s formula as given below:
Let a be the length of the congruent sides and b be the length of the base.
Semi-perimeter (s) = (a + a + b)/2
s = (2a + b)/2
Using the heron’s formula of a triangle,
Area = √[s(s – a)(s – b)(s – c)]
By substituting the sides of an isosceles triangle,
Area = √[s(s – a)(s – a)(s – b)]
= √[s(s – a)2(s – b)]
Or
= (s – a)√[s(s – b)]
which is the required formula to find the area for the given isosceles triangle.
Heron’s Formula for Scalene Triangle
As we know, a scalene triangle has all three unequal sides, thus, we can directly use the original Heron’s formula to find the area.
Area of scalene triangle = √s(s-a)(s-b)(s-c),
where s = (a + b + c)/2
Heron’s Formula For Quadrilateral
Let us learn how to find the area of quadrilateral using Heron’s formula here.
If ABCD is a quadrilateral, where AB||CD and AC & BD are the diagonals.
AC divides the quad.ABCD into two triangles ADC and ABC.
Now we have two triangles here.
Area of quad.ABCD = Area of ∆ADC + Area of ∆ABC
So, if we know the lengths of all sides of a quadrilateral and the length of diagonal AC, then we can use Heron’s formula to find the total area.
Hence, we will first find the area of ∆ADC and area of ∆ABC using Heron’s formula and at last, will add them to get the final value.
Applications of Heron’s Formula
The two major applications of Heron’s formula are:
- To find the area of different types of a triangle (when the length of three sides is given)
- To find the area of a quadrilateral (when the length of all three sides is given)
Solved Examples
Let us now look into some examples to have a brief insight into the topic:
Example 1: Find the area of a trapezium, the length of whose parallel sides is given as 22 cm and 12 cm and the length of the other sides is 14 cm each.
Solution: Let PQRS be the given trapezium in which PQ = 22 cm, SR = 12 cm,
PS=QR=14cm.
Constructions: Draw OR||PS
Now, PORS is a parallelogram in which PS||OR and PO||SR
Therefore, PO=SR=12cm
⇒OQ = PQ-PO = 22 -12 = 10cm
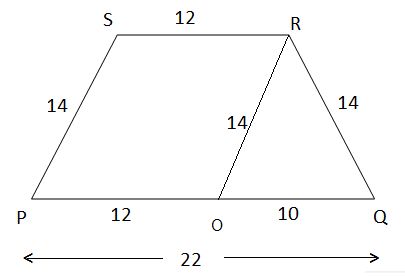
In ∆OQR , we have
Area of ∆OQR =
=
=
=
………(i)
We know that Area =
…………..(ii)
Area of trapezium =
=
=
Example 2: Find the area of the triangle whose sides measure 10 cm, 17 cm and 21 cm. Also, determine the length of the altitude on the side which measures 17 cm.
Solution: s =
=
= 24
Area of Triangle=
= 84 square cm
Taking 17 cm as the base length we need to find the height
Area, A = 1/2 x base x height
1/2 x 17 x h = 84 or h = 168/17 = 9.88 cm (Rounded to the nearest hundredth).
Example 3: A triangle PQR has sides 4 cm, 13 cm and 15 cm. Find the area of the triangle.
Solution:
Semiperimeter of triangle PQR, s = (4+13+15)/2 = 32/2 = 16
By heron’s formula, we know;
A = √[s(s-a)(s-b)(s-c)]
Hence, A = √[16(16-4)(16-13)(16-15)] = √(16 x 12 x 3 x 1) = √576 = 24 sq.cm
Heron’s Formula – Practice Questions
A few practice questions are given below that will help you in improving your knowledge of how to find the area of a given triangle.
- Find the area of a triangle whose perimeter is 54 cm and two of its sides measure 12 cm and 25 cm. [Answer: 90 sq.cm]
- If the length of equal sides of an isosceles triangle is 5 cm and the base is 6 cm, then find its area using heron’s formula. [Answer: 12 sq.cm]
- The sides of a quadrilateral field, taken in order are 26 cm, 27 cm, 7 cm, and 24 cm respectively. The angle contained by the last two sides is a right angle. Find its area. [Answer: 375.85 sq.cm.]
Area of a Triangle - Heron's Formula
The basic formula for the area of a triangle is only helpful if you know the base and the height.
So what do you do if you only know the three side lengths?
There are just two steps.
Step 1: Calculate half the perimeter of the triangle and call it s. 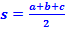
Step 2: Use the s in the following formula: 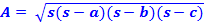
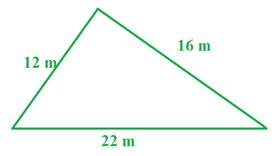
Let's use the formula to determine the area of the triangle above.
Step 1: The perimeter of the triangle is equal to 12 + 22 + 16 = 50
Therefore, the s value is half of 50 or 25.
Step 2: Replace the s in the area formula with 25 and solve.
A = 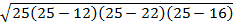
A = 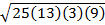
A = 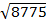
A = 93.7 m2
Here is a couple more example to try.
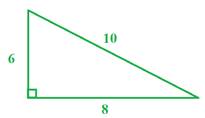
Example 1:
Step 1: Determine half the perimeter.
s = 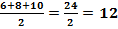
Step 2: Use the s in Heron's formula.
A = 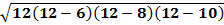
A = 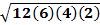
A = 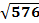
A = 24 units2
Now, this triangle does give the base and height. So let's compare our work to the formula you might be more familiar with using to solve.
A = 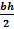
A = 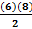
A = 24 units2
Here we have the same answer as we got from using Heron's method.
Example 2:
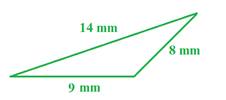
Step1: Determine half the perimeter.
s = 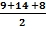
s = 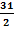
s = 15.5
Step 2: Use the s in Heron's formula.
A = 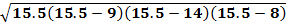
A = 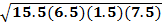
A = 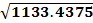
A = 33.7 mm2
When the solution is not rational, the answer can be rounded. In this example, we rounded to the nearest tenth.
Let's Review
If you are given the three sides of a triangle, you can use the perimeter and Heron's formula to determine the area. There are just two steps.
Step 1: Determine half the perimeter.
Step 2: Use the three side lengths and the half perimeter in Heron's formula.
Some of the areas will be irrational numbers. That means that they cannot be represented as a fraction. Instead, they are decimals that never end and never repeat. When this happens, the area can be rounded to whatever place value you may have been asked for.
Area of a Triangle- By Heron's formula
Chapter 12 - Heron's Formula
Heron's Formula
Heron’s formula is used to find the area of a triangle when we know the length of all its sides. It is also termed as Hero’s Formula. We can Heron’s formula to find different types of triangles, such as scalene, isosceles and equilateral triangles. We don’t have to need to know the angle measurement of a triangle to calculate its area, by using Heron’s formula.
What is Heron’s Formula?
Heron’s formula is a formula to calculate the area of triangles, given the three sides of the triangle. This formula is also used to find the area of the quadrilateral, by dividing the quadrilateral into two triangles, along its diagonal.
If a, b and c are the three sides of a triangle, respectively, then Heron’s formula is given by:
|
Semiperimeter, s= Perimeter of triangle/2 = (a+b+c)/2 |
History of Heron’s Formula
Hero of Alexandria was a great mathematician who derived the formula for the calculation of the area of a triangle using the length of all three sides. He also extended this idea to find the area of quadrilateral and also higher-order polygons. This formula has its huge applications in trigonometry such as proving the law of cosines or the law of cotangents, etc.
Heron’s Formula for Triangles
According to Heron, we can find the area of any given triangle, whether it is a scalene, isosceles or equilateral, by using the formula, provided the sides of the triangle.
Suppose, a triangle ABC, whose sides are a, b and c, respectively. Thus, the area of a triangle can be given by;
Where “s” is semi-perimeter = (a+b+c) / 2
And a, b, c are the three sides of the triangle.
Proof of Heron’s Formula
There are two methods by which we can derive Heron’s formula.
- First, by using trigonometric identities and cosine rule.
- Secondly, solving algebraic expressions using the Pythagoras theorem.
Let us see one by one both the proofs or derivation.
Using Cosine Rule
Let us prove the result using the law of cosines:
Let a, b, c be the sides of the triangle and α, β, γ are opposite angles to the sides.
We know that, the law of cosines is
Again, using trig identity, we have
=
Here, Base of triangle = a
Altitude = b sinγ
Now,
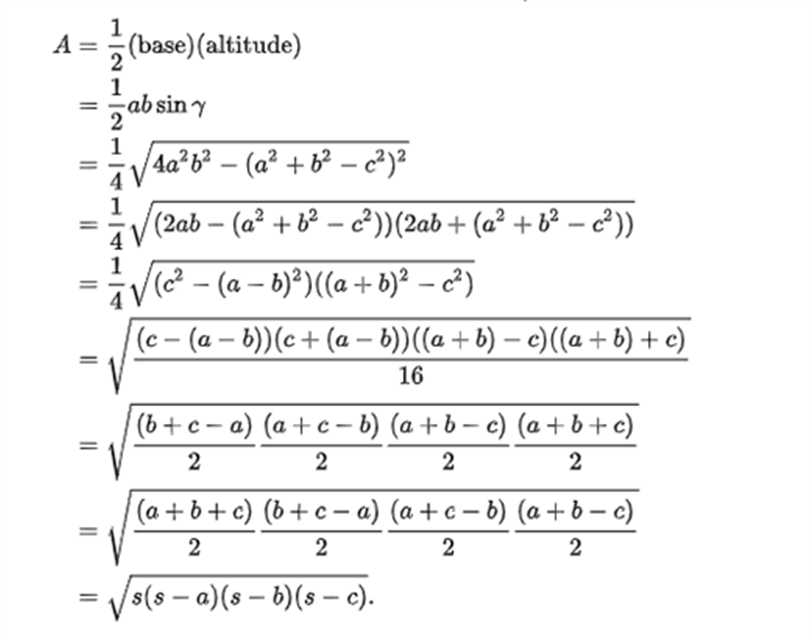
Using Pythagoras Theorem
Area of a Triangle with 3 Sides
Area of ∆ABC is given by
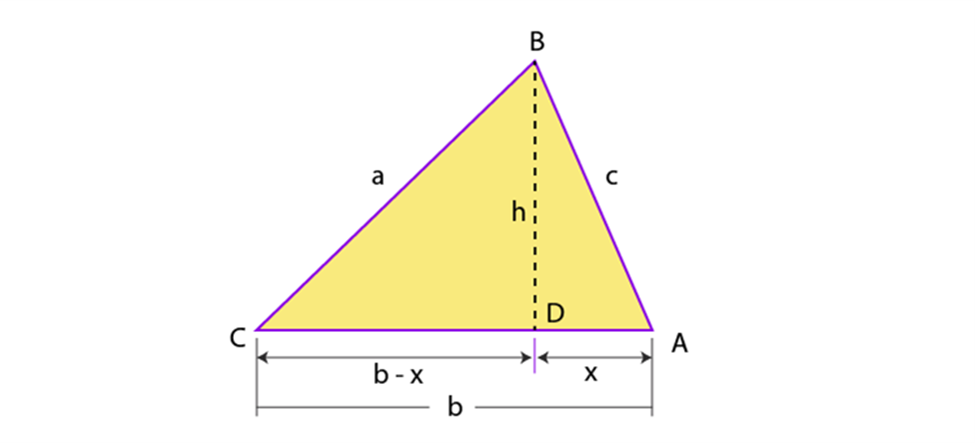
A = 1/2 bh _ _ _ _ (i)
Draw a perpendicular BD on AC
Consider a ∆ADB
x2 + h2 = c2
x2 = c2 − h2—(ii)
⇒x = √(c2−h2)−−−−−−—(iii)
Consider a ∆CDB,
(b−x)2 + h2 = a2
(b−x)2 = a2 − h2
b2 − 2bx + x2 = a2–h2
Substituting the value of x and x2 from equation (ii) and (iii), we get
b2 – 2b√(c2−h2)+ c2−h2 = a2 − h2
b2 + c2 − a2 = 2b√(c2 − h2)
Squaring on both sides, we get;
(b2+c2–a2)2 = 4b2(c2−h2)
The perimeter of a ∆ABC is
P= a+b+c
Substituting the value of h in equation (i), we get;
Semi perimeter(s) =
Note: Heron’s formula is applicable to all types of triangles and the formula can also be derived using the law of cosines and the law of Cotangents.
How to Find the Area Using Heron’s Formula?
To find the area of a triangle using Heron’s formula, we have to follow two steps:
- Find the perimeter of the given triangle
- Then, find the value of the semi-perimeter of the given triangle; S = (a+b+c)/2
- Now use Heron’s formula to find the area of a triangle (√(s(s – a)(s – b)(s – c)))
- Finally, represent the area with the accurate square units (such as m2, cm2, in2, etc.)
Heron’s Formula for Equilateral Triangle
As we know the equilateral triangle has all its sides equal. To find the area of the equilateral triangle let us first find the semi perimeter of the equilateral triangle will be:
s = (a+a+a)/2
s=3a/2
where a is the length of the side.
Now, as per the heron’s formula, we know;
Since, a = b = c
Therefore,
A = √[s(s-a)3]
which is the required formula.
Heron’s Formula for Isosceles Triangle
An isosceles triangle has two of its sides equal and the angles corresponding to these sides are congruent. To find the area of an isosceles triangle, we can derive the heron’s formula as given below:
Let a be the length of the congruent sides and b be the length of the base.
Semi-perimeter (s) = (a + a + b)/2
s = (2a + b)/2
Using the heron’s formula of a triangle,
Area = √[s(s – a)(s – b)(s – c)]
By substituting the sides of an isosceles triangle,
Area = √[s(s – a)(s – a)(s – b)]
= √[s(s – a)2(s – b)]
Or
= (s – a)√[s(s – b)]
which is the required formula to find the area for the given isosceles triangle.
Heron’s Formula for Scalene Triangle
As we know, a scalene triangle has all three unequal sides, thus, we can directly use the original Heron’s formula to find the area.
Area of scalene triangle = √s(s-a)(s-b)(s-c),
where s = (a + b + c)/2
Heron’s Formula For Quadrilateral
Let us learn how to find the area of quadrilateral using Heron’s formula here.
If ABCD is a quadrilateral, where AB||CD and AC & BD are the diagonals.
AC divides the quad.ABCD into two triangles ADC and ABC.
Now we have two triangles here.
Area of quad.ABCD = Area of ∆ADC + Area of ∆ABC
So, if we know the lengths of all sides of a quadrilateral and the length of diagonal AC, then we can use Heron’s formula to find the total area.
Hence, we will first find the area of ∆ADC and area of ∆ABC using Heron’s formula and at last, will add them to get the final value.
Applications of Heron’s Formula
The two major applications of Heron’s formula are:
- To find the area of different types of a triangle (when the length of three sides are given)
- To find the area of a quadrilateral (when the length of all three sides are given)
Solved Examples
Let us now look into some examples to have a brief insight into the topic:
Example 1: Find the area of a trapezium, the length of whose parallel sides is given as 22 cm and 12 cm and the length of other sides is 14 cm each.
Solution: Let PQRS be the given trapezium in which PQ = 22 cm, SR = 12 cm,
PS=QR=14cm.
Constructions: Draw OR||PS
Now, PORS is a parallelogram in which PS||OR and PO||SR
Therefore, PO=SR=12cm
⇒OQ = PQ-PO = 22 -12 = 10cm
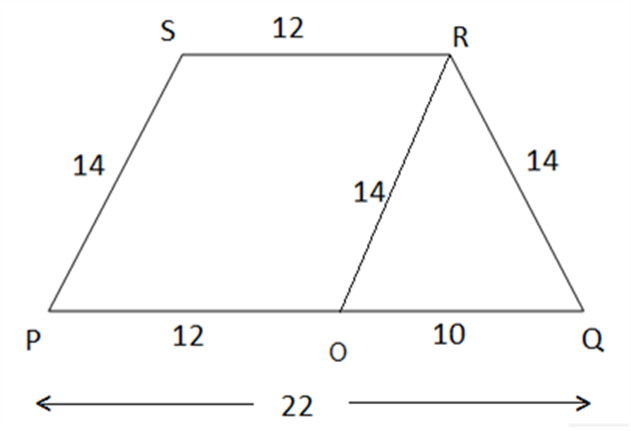
In ∆OQR , we have
Area of ∆OQR =
=
=
=
………(i)
We know that Area =
…………..(ii)
Area of trapezium =
=
=
Example 2: Find the area of the triangle whose sides measure 10 cm, 17 cm and 21 cm. Also, determine the length of the altitude on the side which measures 17 cm.
Solution: s =
=
= 24
Area of Triangle=
= 84 square cm
Taking 17 cm as the base length we need to find the height
Area, A = 1/2 x base x height
1/2 x 17 x h = 84 or h = 168/17 = 9.88 cm (Rounded to the nearest hundredth).
Example 3: A triangle PQR has sides 4 cm, 13 cm and 15 cm. Find the area of the triangle.
Solution:
Semiperimeter of triangle PQR, s = (4+13+15)/2 = 32/2 = 16
By heron’s formula, we know;
A = √[s(s-a)(s-b)(s-c)]
Hence, A = √[16(16-4)(16-13)(16-15)] = √(16 x 12 x 3 x 1) = √576 = 24 sq.cm
Heron’s Formula – Practice Questions
A few practice questions are given below that will help you in improving your knowledge of how to find the area of a given triangle.
- Find the area of a triangle whose perimeter is 54 cm and two of its sides measure 12 cm and 25 cm. [Answer: 90 sq.cm]
- If the length of equal sides of an isosceles triangle is 5 cm and base is 6 cm, then find its area using heron’s formula. [Answer: 12 sq.cm]
- The sides of a quadrilateral field, taken in order are 26 cm, 27 cm, 7 cm, 24 cm respectively. The angle contained by the last two sides is a right angle. Find its area. [Answer: 375.85 sq.cm.]
Area of a Triangle - Heron's Formula
The basic formula for the area of a triangle is only helpful if you know the base and the height.
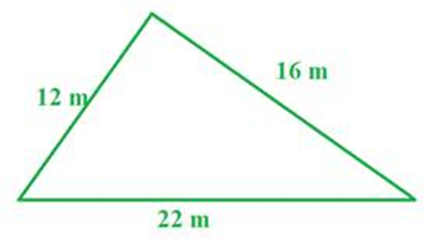
So what do you do if you only know the three side lengths?
There are just two steps.
Step 1: Calculate half the perimeter of the triangle and call it s. 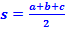
Step 2: Use the s in the following formula: 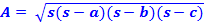

Let's use the formula to determine the area of the triangle above.
Step 1: The perimeter of the triangle is equal to 12 + 22 + 16 = 50
Therefore, the s value is half of 50 or 25.
Step 2: Replace the s in the area formula with 25 and solve.
A = 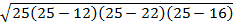
A = 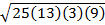
A = 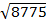
A = 93.7 m2
Here are a couple more example to try.
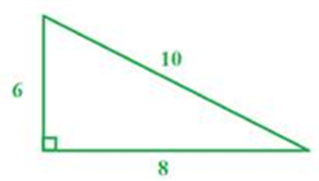
Example 1:
Step 1: Determine half the perimeter.
s = 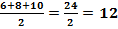
Step 2: Use the s in Heron's formula.
A = 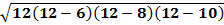
A = 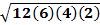
A = 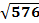
A = 24 units2
Now, this triangle does give the base and height. So let's compare our work to the formula you might be more familiar with using to solve.
A = 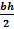
A = 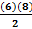
A = 24 units2
Here we have the same answer as we got from using Heron's method.
Example 2:
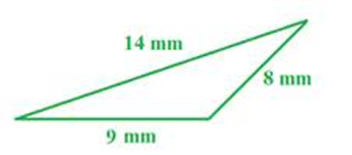
Step1: Determine half the perimeter.
s = 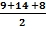
s = 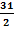
s = 15.5
Step 2: Use the s in Heron's formula.
A = 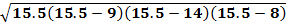
A = 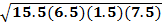
A = 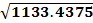
A = 33.7 mm2
When the solution is not rational, the answer can be rounded. In this example, we rounded to the nearest tenth.
Let's Review
If you are given the three sides of a triangle, you can use the perimeter and Heron's formula to determine the area. There are just two steps.
Step 1: Determine half the perimeter.
Step 2: Use the three side lengths and the half perimeter in Heron's formula.
Some of the areas will be irrational numbers. That means that they cannot be represented as a fraction. Instead they are decimals that never end and never repeat. When this happens, the area can be rounded to whatever place value you may have been asked for.
Application of Heron's formula in finding areas of quadrilaterals
- Books Name
- ABCD CLASSES Mathematics Book
- Publication
- ABCD CLASSES
- Course
- CBSE Class 9
- Subject
- Mathmatics
Application of Heron’s Formula in Finding Areas of Quadrilaterals
In geometry, the shapes can be classified into two-dimensional shapes and three-dimensional shapes. 2D shapes are the plane figures, which are made up of two dimensions such as length and breadth, whereas 3D shapes are the solid figures, which are made up of three dimensions such as length, breadth and height. We know that a triangle is a 2D shape, whose area can be determined by using the formula ½ × b × h if the base and height of the triangle are given. What if only the sides of a triangle are given? How to find the area of a triangle if the side lengths are given?
The solution to this is by applying Heron’s formula. One can find the area of a triangle using Heron’s formula, only if the side measurements are given. Now, let us have a quick recall about Heron’s formula.
Heron’s Formula – Finding Area of a Triangle
If a, b and c are the sides of a triangle, and s is the semi perimeter of a triangle, then the formula to find the area of the triangle using Heron’s formula is:
Area of Triangle = √[s(s-a)(s-b)(s-c)] Square units.
Note: s is the semi perimeter, which means half the perimeter of a triangle, and it is found using the formula:
s = (a+b+c)/2.
Application of Heron’s Formula in Finding Areas of Quadrilaterals Examples
Heron’s formula is also applicable to find the area of a quadrilateral if the quadrilaterals are divided into triangular parts. Once the quadrilaterals are divided into triangular forms, apply Heron’s formula to find the area of individual triangular parts. After finding the areas of each triangular part, add all the areas to find the area of the quadrilateral. Now, let us understand the application of Heron’s formula in finding the areas of quadrilaterals with the help of solved examples.
Example 1:
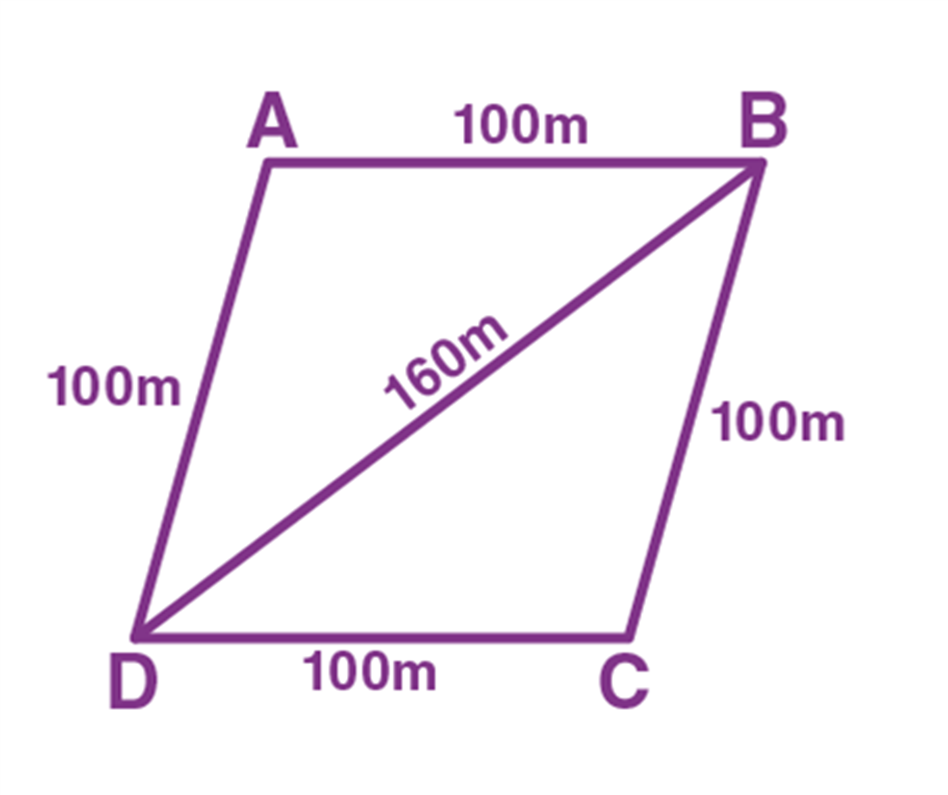
Masha has a piece of land that is shaped like a rhombus. She wants her one son and one daughter to work on the land to produce different crops. So, she has divided the land into two equal parts. Determine how much area each of them will get for their crop production if the perimeter of the land is 400 m and one of its diagonals is 160 m.
Solution: Given: ABCD is a rhombus-shaped land.
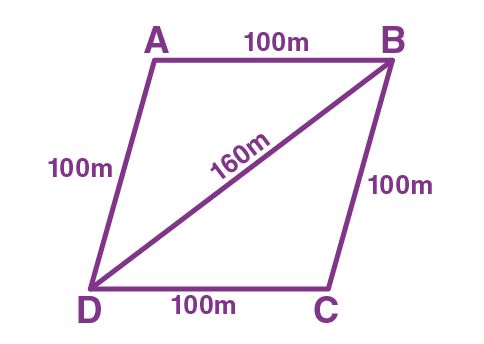
Given that, perimeter = 400 m
Therefore, each side length of rhombus = 400/4 = 100 cm.
Thus, we can take that AD = AB = 100 m
Diagonal, BD = 160 m.
Now, consider the triangle ABD,
The semiperimeter of ∆ ABD, s = (100+ 100+ 160)/2
s = 360/2 m
s = 180 m.
Therefore, the semi perimeter of a triangle = 180m.
Thus, the area of triangle ABD = √[s(s-a)(s-b)(s-c)] square units.
Now, substitute s= 180 m, a= 100, b= 100 and c= 160 in the Heron’s formula, we get
A = √[180 (180 – 100)(180 – 100)(180 – 160)] m2
A = √[180(80)(80)(20)] m2
A = √23040000 m2
A = 4800 m2
Hence, each of them will get land for their crop production of 4800 m2
Example 2:
The school students staged a rally for a cleanliness campaign. They walked through the lane into two groups. One group walked through the lanes AB, BC and CA, and the other group walked through the lanes AC, CD and DA as shown in the figure. They cleaned the area enclosed within the lanes. Find the total area cleaned by the students (Neglect the width of the lane), if AB = 9m, BC = 40m, CD = 15m, DA = 28m and ∠B = 90º. Also, find which group cleaned more area and how much.
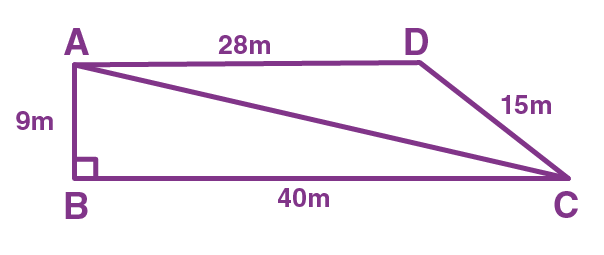
Solution:
Given that, AB = 9m, BC = 40m, and ∠B = 90º
Therefore, AC = √(92+402) = √(81+1600)
AC = √1681 = 41m.
Thus, the first group of students cleaned the area of triangle ABC (which is right-angled)
Therefore, the area of triangle = (½)(40)(9) m2
A = 180m2
Hence, the first group of students to clean the lane ABC is 180m2.
Now, the second group of students cleans the lane ACD, which is a scalene triangle having side lengths 41m, 28m and 15m.
Now, use Heron’s formula to find the area of ACD.
So, s = (41+28+15)/2
s = 42m
By, using Heron’s formula, A =√[s(s-a)(s-b)(s-c)], we get
A = √[42(42-41)(42-28)(42-15)] m2
A = √[42(1)(14)(27)] m2
A = √15876 m2
A = 126 m2
Hence, the second group of students cleaned the lane ACD is 126m2.
The total area cleaned by all the students = (180+126)m2 = 306m2.
Therefore, the first group of students cleaned more lane areas than the area cleaned by the second group of students.
Practice Problems
Solve the following problems on the application of Heron’s formula in finding areas of the quadrilateral.
- A field is in the shape of a rhombus and it has green grass for 18 cows to graze. Determine how much area of grass field each cow will be getting, if each side of the rhombus is 30m and its longest diagonal is 48m.
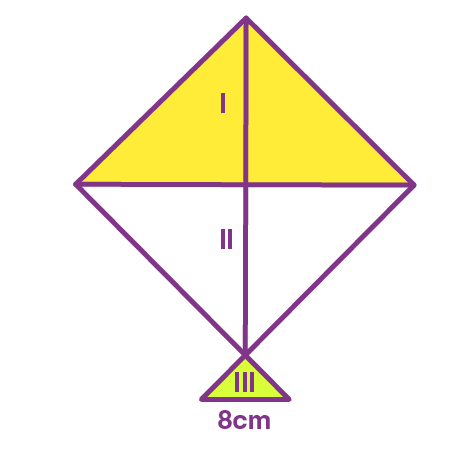
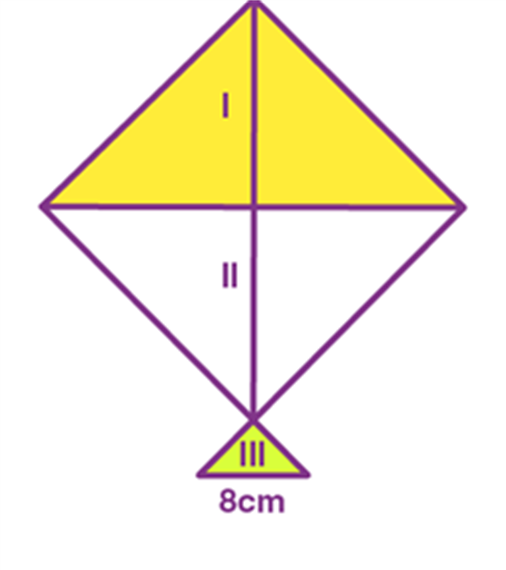
- A kite is in a square shape. Its diagonal is 32 cm and its isosceles triangle of base 8 cm and side 6 cm each is made of three different shades as shown in the figure. Find how much paper of each shade has been used in it to make a kite.
Application of Heron's formula in finding areas of quadrilaterals
Application of Heron’s Formula in Finding Areas of Quadrilaterals
In geometry, the shapes can be classified into two-dimensional shapes and three-dimensional shapes. 2D shapes are the plane figures, which are made up of two dimensions such as length and breadth, whereas 3D shapes are the solid figures, which are made up of three-dimensions such as length, breadth and height. We know that a triangle is a 2D shape, whose area can be determined by using the formula ½ × b × h, if base and height of the triangle are given. What if only the sides of a triangle are given? How to find the area of a triangle if the side lengths are given?
The solution to this is by applying Heron’s formula. One can find the area of a triangle using Heron’s formula, only if the side measurements are given. Now, let us have a quick recall about Heron’s formula.
Heron’s Formula – Finding Area of a Triangle
If a, b and c are the sides of a triangle, and s is the semiperimeter of a triangle, then the formula to find the area of triangle using Heron’s formula is:
Area of Triangle = √[s(s-a)(s-b)(s-c)] Square units.
Note: s is the semiperimeter, which means half the perimeter of a triangle, and it is found using the formula:
s = (a+b+c)/2.
Application of Heron’s Formula in Finding Areas of Quadrilaterals Examples
Heron’s formula is also applicable to find the area of a quadrilateral if the quadrilaterals are divided into triangular parts. Once the quadrilaterals are divided into triangular forms, apply Heron’s formula to find the area of individual triangular parts. After finding the areas of each triangular part, add all the areas to find the area of quadrilateral. Now, let us understand the application of Heron’s formula in finding the areas of quadrilaterals with the help of solved examples.
Example 1:
Masha has a piece of land which is shaped like a rhombus. She wants her one son and one daughter to work on the land to produce different crops. So, she has divided the land into two equal parts. Determine how much area each of them will get for their crop production if the perimeter of the land is 400 m and one of its diagonals is 160 m.
Solution:
Given: ABCD is a rhombus-shaped land.
Given that, perimeter = 400 m
Therefore, each side length of rhombus = 400/4 = 100 cm.
Thus, we can take that AD = AB = 100 m
Diagonal, BD = 160 m.
Now, consider the triangle ABD,
The semiperimeter of ∆ ABD, s = (100+ 100+ 160)/2
s = 360/2 m
s = 180 m.
Therefore, the semi perimeter of a triangle = 180m.
Thus, the area of triangle ABD = √[s(s-a)(s-b)(s-c)] square units.
Now, substitute s= 180 m, a= 100, b= 100 and c= 160 in the Heron’s formula, we get
A = √[180 (180 – 100)(180 – 100)(180 – 160)] m2
A = √[180(80)(80)(20)] m2
A = √23040000 m2
A = 4800 m2
Hence, each of them will get land for their crop production of 4800 m2
Example 2:
The school students staged a rally for a cleanliness campaign. They walked through the lane into two groups. One group walked through the lanes AB, BC and CA, and the other group walked through the lanes AC, CD and DA as shown in the figure. They cleaned the area enclosed within the lanes. Find the total area cleaned by the students (Neglect the width of the lane), if AB = 9m, BC = 40m, CD = 15m, DA = 28m and ∠B = 90º. Also, find which group cleaned more area and how much.
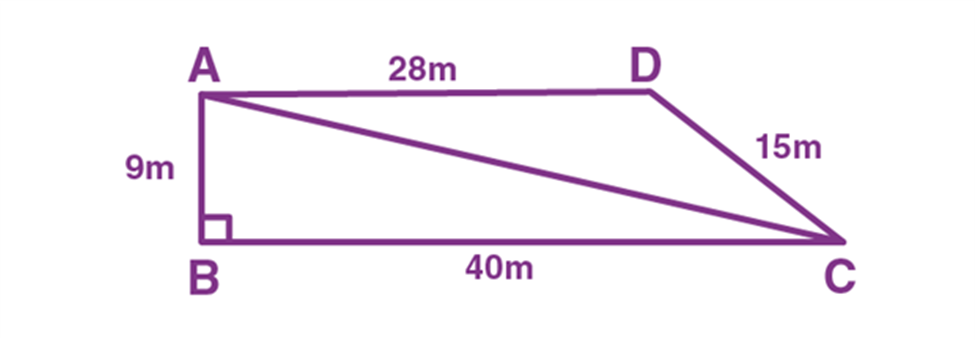
Solution:
Given that, AB = 9m, BC = 40m, and ∠B = 90º
Therefore, AC = √(92+402) = √(81+1600)
AC = √1681 = 41m.
Thus, the first group of students cleaned the area of triangle ABC (which is right-angled)
Therefore, the area of triangle = (½)(40)(9) m2
A = 180m2
Hence, the first group of students to clean the lane ABC is 180m2.
Now, the second group of students clean the lane ACD, which is a scalene triangle having side lengths 41m, 28m and 15m.
Now, use Heron’s formula to find the area of ACD.
So, s = (41+28+15)/2
s = 42m
By, using Heron’s formula, A =√[s(s-a)(s-b)(s-c)], we get
A = √[42(42-41)(42-28)(42-15)] m2
A = √[42(1)(14)(27)] m2
A = √15876 m2
A = 126 m2
Hence, the second group of students cleaned the lane ACD is 126m2.
The total area cleaned by all the students = (180+126)m2 = 306m2.
Therefore, the first group of students cleaned more lane areas than the area cleaned by the second group of students.
Practice Problems
Solve the following problems on the application of Heron’s formula in finding areas of the quadrilateral.
- A field is in the shape of a rhombus and it has green grass for 18 cows to graze. Determine how much area of grass field each cow will be getting, if each side of the rhombus is 30m and its longest diagonal is 48m.
- A kite is in a square shape. Its diagonal is 32 cm and its isosceles triangle of base 8 cm and side 6 cm each is made of three different shades as shown in the figure. Find how much paper of each shade has been used in it to make a kite.

 ABCD CLASSES
ABCD CLASSES
