Chapter 11: Mensuration

Mensuration

Trapezium

Recalling trapezium

A trapezium is a quadrilateral with one pair of opposite side parallel.

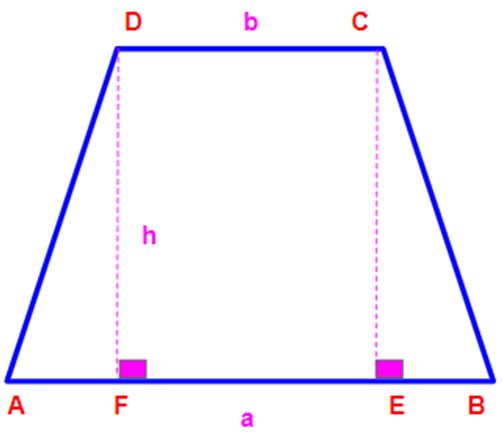
For the trapezium ABCD, the following will be true:

• AB||DC,where AB and DC are parallel sides
• CE⊥AB, where CE is perpendicular to AB
• DF⊥AB, where DF is perpendicular to AB
• CE=DF=h, where h is the height of the trapezium

Area, perimeter of trapezium

Area of trapezium: To obtain the area of a trapezium, multiply the sum of the bases by the height and then divide by 2.

The area of a trapezium is computed with the following formula:

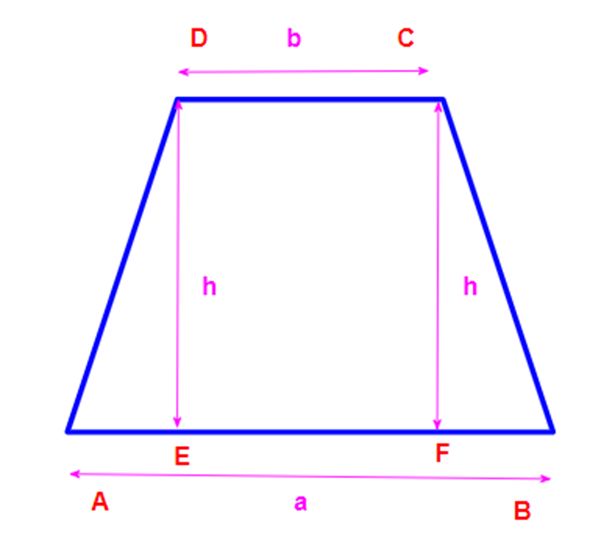
Area of trapezium = 12×(a+b)×(h) square units.

(where a and b is bases (parallel sides) and h is leg or height (between the non-parallel sides)).

Area of the trapezium ABCD:

Proof: Area of a trapezium ABCD.

Area of trapezium ABCD = 12(AB+DC)×(h) squareunits.

= area of triangle (DEA) + area of rectangle (DEFC) + area of triangle (CFB)

= 12×AE×DE + DE×EF + 12×FB×CF

= 12×AE×h + h×EF + 12×FB×h

= 12×(AE+2EF+FB)×h

= 12×(AE+EF+CD+FB)×h

= 12×(AE+EF+FB+CD)×h

= 12×(AB+CD)×(h)

= 12×(a+b)×(h)

= 12×(sum of parallel side) ×(height) square units.

Therefore, Area of trapezium ABCD= 12×(a+b)×(h) or

Perimeter of trapezium: The Perimeter is the sum of all side lengths.

The perimeter of a trapezium is computed with the following formula:

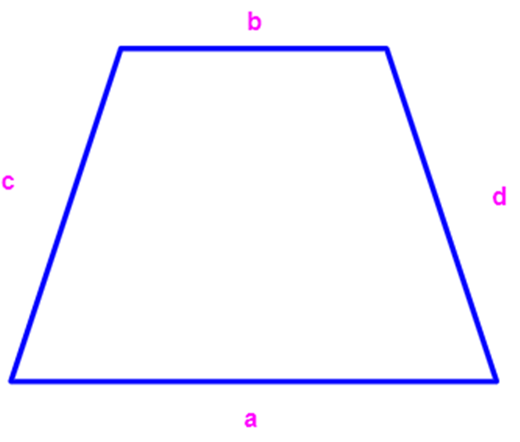
Perimeter of trapezium = a+b+c+d (where a, b are denoted as bases (parallel sides) and c, d are denoted as legs (non-parallel sides)).

Area of Quadrilaterals and Polygons

Area of a general quadrilateral

We know that a quadrilateral is made up of four sides. Any quadrilateral can be divided into two triangles with the help of a diagonal. This process of dividing a quadrilateral into triangles is called triangulation.

Let us look at the figure given below to know how a quadrilateral would look like after triangulation.

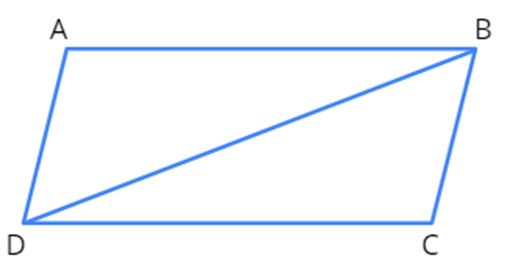
Here, △ABD and △BCD are formed after triangulation.

To find the area of the quadrilateral, we should know the values of h1 and h2. h1 and h2 are the perpendiculars drawn from the diagonal to the vertices. Let us look at the figure given below for a better understanding.

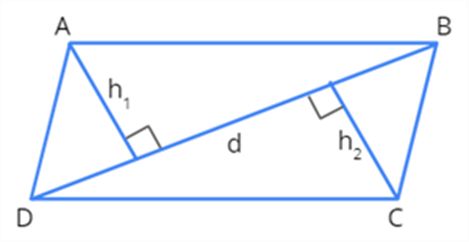
From the figure given above, we can come to the following inferences.

ABCD is a quadrilateral with d as the diagonal and h1 and h2 as its heights.

Area of quadrilateral ABCD= (Area of△ABD) + (Area of△BCD)

[Since the diagonal is divided into two triangles after triangulation]

= (12×BD×h1) + (12×BD×h2)

[Since,Area of a triangle=12×b×h,where b and h are its base and height respectively]

= 12×BD×(h1+h2)

= 12×d×(h1+h2)

Therefore, Area of a quadrilateral = 12d(h1+h2) square units.

Area of a special quadrilateral (Rhombus),

A special quadrilateral is nothing but a rhombus. To find the area of a rhombus, we can use the same triangulation method as used in finding the area of a general quadrilateral.

A rhombus after triangulation is given below.

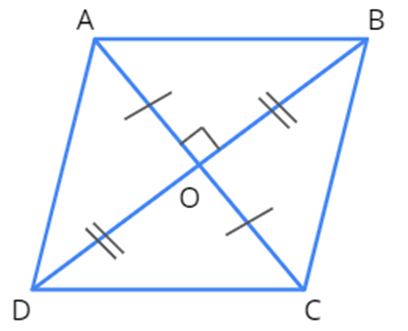
From the figure given above, we can come to the following inferences.

ABCD is a rhombus with diagonals AC and BD.

Let AC be d1 and BD be d2. The diagonals d1 and d2 intersect at O.

Also, as per the properties of a rhombus, the diagonals bisect each other.

Area of the rhombus ABCD= (Area of △ABD)) + (Area of △BCD)

= 12×BD×OA + 12×BD×OC

= 12×BD×(OA+OC)

= 12×BD×AC

[Since AC=OA+OC]

= 12×d1×d2

[Since we have assumed that AC=d1, and BD=d2]

Therefore, area of a rhombus=12×d1×d2 square units or the area of the rhombus is half the product of its diagonals.

Area of a polygon

A polygon is any shape with a minimum of three sides.

Let us consider the following pentagon ABCDE and try to find its area.

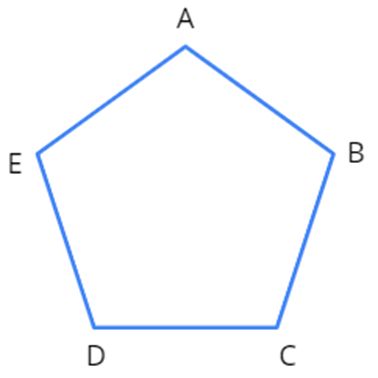
Area of a pentagon can be found in two ways.

Type 1

Let us use the method of triangulation using two diagonals.

Let us look at the figure given below for a better understanding.

Area of a pentagon=Area of △AED+Area of △ABD+Area of △BCD

Type 2

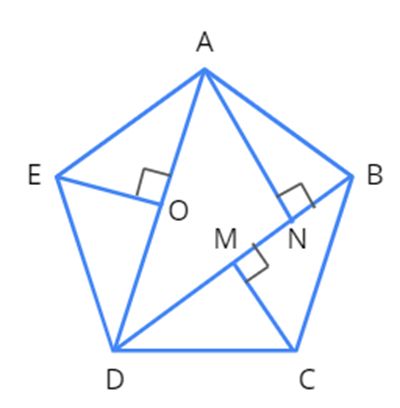
Another way of obtaining the area of a pentagon is by drawing one diagonal and drawing two perpendiculars to that diagonal.

Let us look at the figure given below for a better understanding.

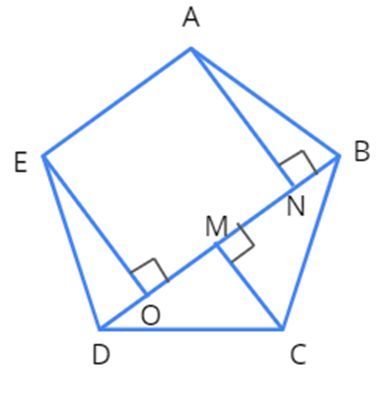
In the figure given above, BD is the diagonal, EO and AN are the two perpendiculars to BD.

Here, Area of a pentagon=Area of △ODE+Area of △BCD+Area of trapezium AEON+Area of △ABN

Surface Area of Cube, Cubiod and Cylinder

Surface area of cubes and cuboids

The surface area of a cuboid

We know that a cuboid has 6 faces and has 3 dimensions, namely length, breadth and height.

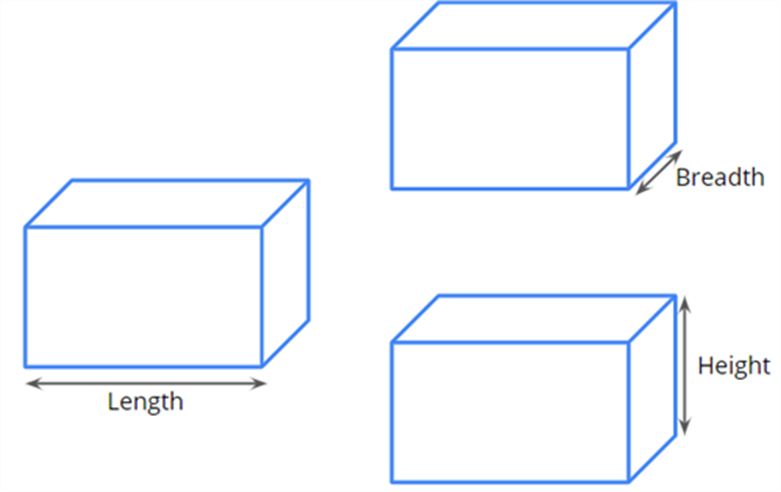
Let us consider a cuboidal cardboard box. Do you know how much cardboard has been used to construct that box?

We can find the amount of cardboard used by finding the box's total surface area.

First, let us cut open the box.

The net of the box looks like this.

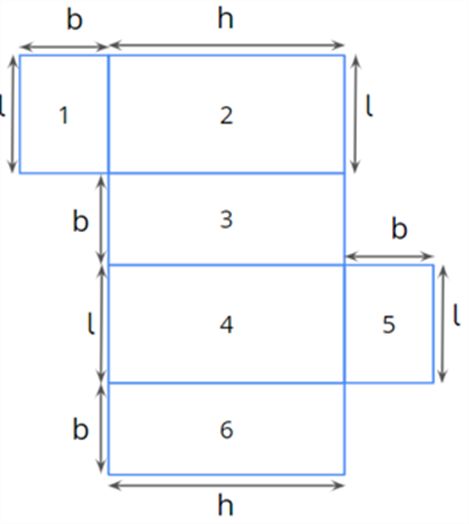
The total surface area of the cardboard box = Area 1 + Area 2 + Area 3 + Area 4 + Area 5 + Area 6

=(l×b)+(l×h)+(b×h)+(l×h)+(l×h)+(l×b)+(b×h)

=2×[(l×b)+(l×h)+(b×h)]

=2×(lb+lh+bh)

In other words, The total surface area of a cuboid=2(lb+lh+bh)

What forms the lateral surface of the cuboid?

The 4 faces (excluding the top and bottom faces) form the lateral surface of the cuboid.

Let us look at the representation below.

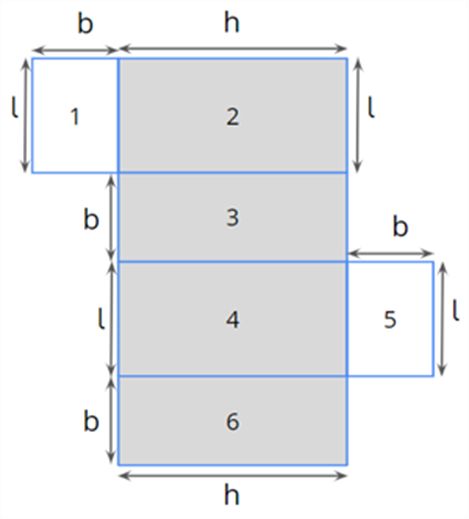
Here, the shaded portion forms the lateral surface of the cuboid.

The lateral surface of a cuboid = Area 2 + Area 3 + Area 4 + Area 6

=(l×h)+(b×h)+(l×h)+(b×h)

=h×(2l+2b)

The lateral surface of a cuboid=2h×(l+b)

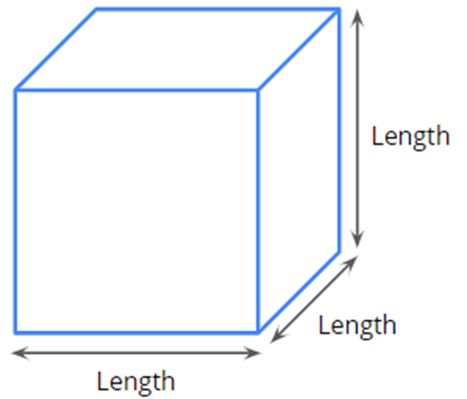
The surface area of a cube

Cube is a special type of cuboid whose length, breadth and height are all equal.

Let us consider the total surface area of the cuboid to find the total surface area of the cube.

The total surface of a cuboid=2×[(l×b)+(l×h)+(b×h)]

Since the length, breadth and height of a cube are equal, we can substitute 'l' in the place of 'b' and 'h'.

The total surface of a cube=2(l×l+l×l+l×l)  =2(3×l2)

The total surface of a cube=6×l2

Let us now consider the lateral surface area of a cuboid.

The lateral surface of a cuboid=2h×(l+b)

Let us now substitute 'l' in the place of 'b' and 'h' to find the lateral surface area of the cube.

The lateral surface of a cube=2l×(l+l)   =2l+2l

The lateral surface of a cube=4×l2

The surface area of a cylinder

A cylinder has two plane ends. Each plane end is circular, and these two plane ends are parallel to each other.

Also, a cylinder has two dimensions, namely radius and height.

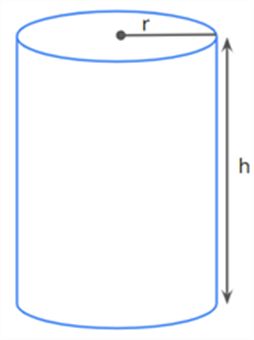
The net of a cylinder looks like this.

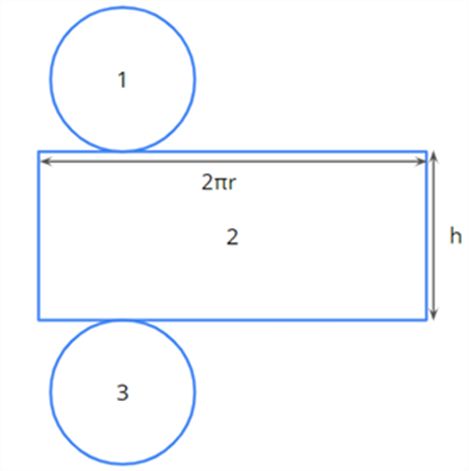
The total surface area of a cylinder = Area 1 + Area 2 + Area 3

=πr2+2πrh+πr2

[Since Area 1 and Area 3 are circles]

=2πr2+2πrh

=2πr(r+h)

Let us now look at the lateral surface of the cylinder.

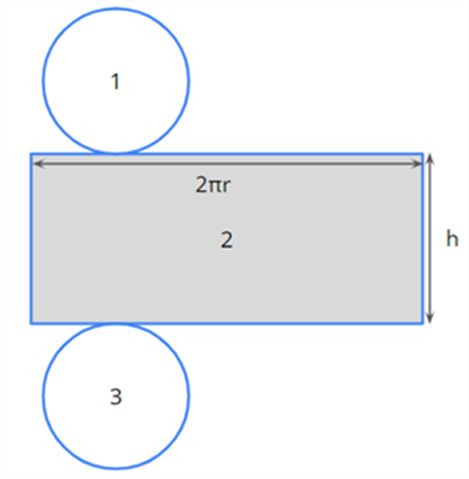
The shaded portion forms the lateral surface of the cylinder.

The lateral (or curved) surface area of a cylinder = Area 2 = 2πrh

Volume of cube, cubiod and cylinder

Volume of a cuboid and a cube

 A cuboid is a rectangular solid with six rectangular faces. It also has three dimensions, namely length, breadth, and height.

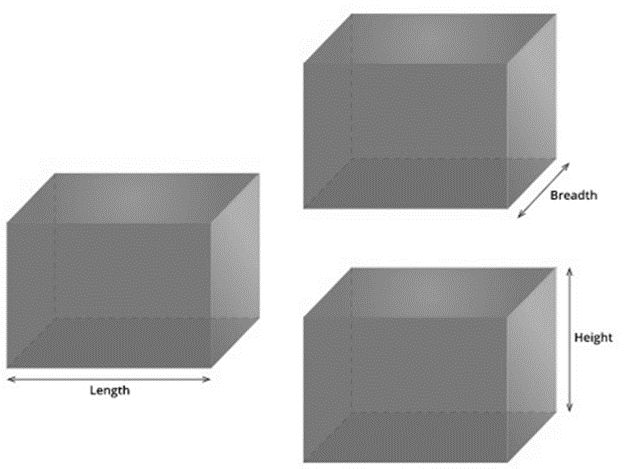
The product of all three dimensions of a cuboid is its volume.

Therefore, The volume of a cuboid=Length×Breadth×Height.

It can also be written as The volume of a cuboid=Area of the base×Breadth.

[Since, Area of the base=Length×Height]

The volume of a cubeIn a cube, all sides are equal.

The volume of a cube can be derived from the formula to find the volume of a cuboid.

The volume of a cuboid=Length×Breadth×Height

Since all sides in a cube are equal, we should substitute Length in the place of Breadth and Height.

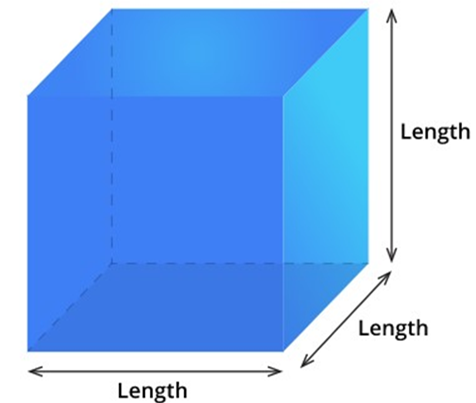
Thus, The volume of a cube=Length×Length×Length=(Length)3

Volume of a cylinder

A cylinder has two dimensions, namely radius and height.

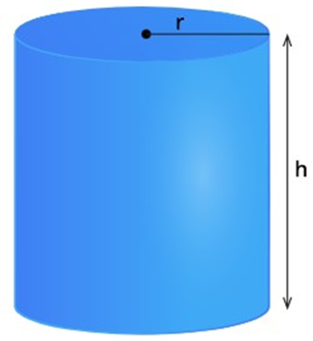
The volume of a cylinder=The area of the base×Height

=π×r2×h

[Since the base of a cylinder is a circle, the area of the base=πr2]