- Books Name
- CBSE Class 7 Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 7
- Subject
- Mathmatics
OTHER TYPES OF ANGLES
1. Complementary angles: If the sum of the measures of two angles is 90° then the angles are complementary angles and each angle is complement of the other angle.
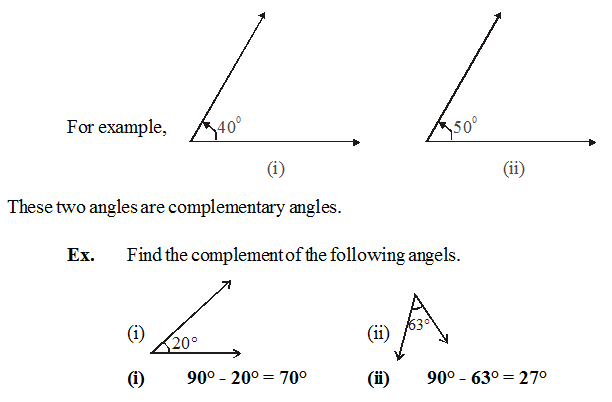
2. Supplementary angles: If the sum of the measures of two angles is 1800 then the angles are called supplementary angles and each angle is said to be the supplement of the other.
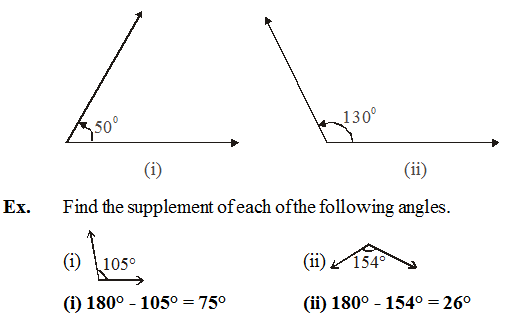
Illustration 1
Find the measure of an angle which is complement of itself.
Solution
Let the measure of the angle be xº. Then, the measure of its complement is given to be xº.
Since, the sum of the measures of an angle and its complement is 90º.
∴ xº + xº = 90º
⇒ 2xº = 90º
⇒ xº = 45
Hence, the measure of the angle is 45º.
Illustration 2
Two supplementary angles differ by 34º. Find the angles.
Solution
Let one angle be xº. Then, the other angle is (x + 34)º.
Now, xº and (x + 34)º are supplementary angles.
∴ xº + (x + 34)º = 180º
⇒ 2xº + 34º = 180º
⇒ 2xº = 180º – 34º
⇒ 2xº = 146º
⇒ xº = 73º.
Hence, the measures of two angles are 73º and 73º + 34º = 107º.
3. Adjacent angle :
If a pair of angles have :
a. a common vertex
b. a common arm
c. and their non-common arms are on either side of the common arm. Such pairs of angles are called adjacent angles. Adjacent angles have no common interior points.
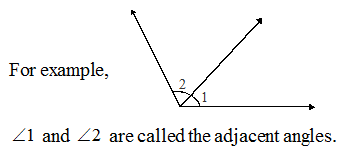
4. Linear pair: A pair of adjacent angles whose non-common sides are opposite rays. The angles in a linear pair are supplementary.
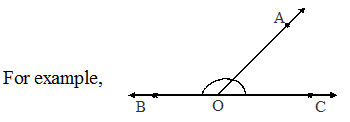
Here OA is common arm and OB and OC form opposite rays. ∠∠180°
By seeing this fig. we can say that if a ray stand on a line, then the sum of the two adjacent angles so formed is 180°.
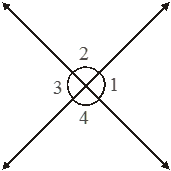
5. Vertically opposite angles


 ReginaTagebücher
ReginaTagebücher
 Param Publication
Param Publication
