- Books Name
- CBSE Class 7 Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 7
- Subject
- Mathmatics
Ratio and Proportion
Ratio
A ratio is the comparison of two or more quantities of same kind using division or we can define ratio of two quantities a and b of the same kind in the same units as a fraction ![]() which is written generally as a : b (read as ‘a’ is to ‘b’). In the ratio a : b, ‘a’ is called the first term or antecedent and ‘b’ is called the second term or consequent.
which is written generally as a : b (read as ‘a’ is to ‘b’). In the ratio a : b, ‘a’ is called the first term or antecedent and ‘b’ is called the second term or consequent.
RATIO IN SIMPLEST FORM OR LOWEST TERM
A ratio is said to be in its simplest form or lowest terms when its terms do not have common factor except 1.
Note :
1. Ratio only exists between quantities of same kind :
(i) There exists no ratio between the height of a child and the weights of a child.
(ii) We cannot write a ratio between the age of a student and the marks obtained by the student.
2. To find a ratio between the quantities of same kind, quantities should be expressed in same units.
3. Ratio has no unit.
(I) Comparison of Ratio: Two ratios can be compared by converting them to like fractions. If the two fractions are equal, we say that two given ratios are equivalent.
Illustration 1
Express the ratio 36 : 81 in the simplest form.
Solution
H.C.F. of 36 and 81 is 9
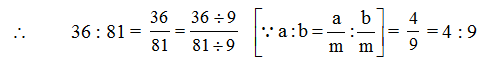
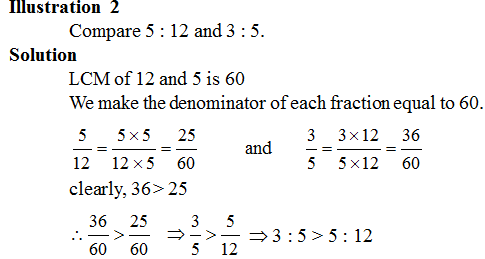
- Books Name
- class 7 Mathematics Book
- Publication
- ReginaTagebücher
- Course
- CBSE Class 7
- Subject
- Mathmatics
Chapter -8
Comparing Quantities
The Ratio
Introduction to ratio
Ratios are used to compare quantities.
Symbol ':' is used to denote ratio.
• For a ratio, the two quantities must be in the same unit. If they are not, they should be expressed in the same unit before the ratio is taken.
Example: If there are four girls and seven boys in a class, then the ratio of number of girls to number of boys is 4:7.

g. Cost of 6 pens is Rs 90. What would be the cost of 10 such pens?
Solution: Cost of 6 pens = Rs 90
Cost of 1 pen = 90 ÷ 6 = Rs 15
Hence, cost of 10 pens = 10 × 15 = Rs 150.
Application of ratios
Ratios have numerous applications in various fields on a daily basis.
- Used in finance - Current ratio, debt-equity ratio, etc.
- Used in chemistry to know the ratio of quantity of chemicals to be mixed in a chemical reaction.
- Used to solved mathematical problems involving - speed-distance-time, boat and stream problems,etc

Equivalent ratios
- By multiplying numerator and denominator of a rational number by a non zero integer, we obtain another rational number equivalent to the given rational number. These are called equivalent ratio.


Example
![]()
And
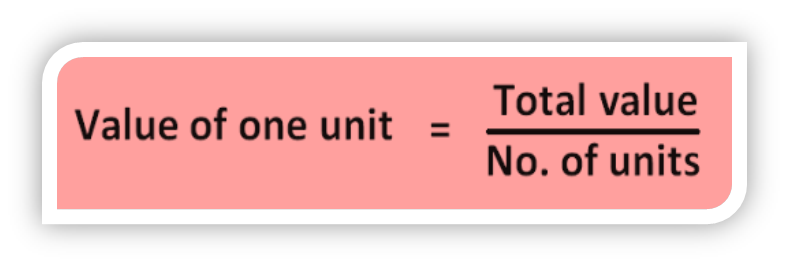
Unitary method
Unitary method is the method of finding the value of one unit (unit rate) at first and then the value of required number of units

 Param Publication
Param Publication
 ReginaTagebücher
ReginaTagebücher
