- Books Name
- CBSE Class 7 Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 7
- Subject
- Mathmatics
Equivalent Ratio
A ratio obtained by multiplying or dividing the numerator and denominator of a given ratio by the same non-zero number is called an equivalent ratio. A ratio remains unchanged if both of its terms are multiplied or divided by same non zero quantity.
If n ≠ 0, then :
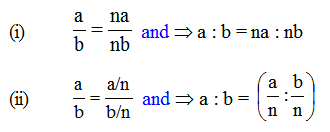

- Books Name
- class 7 Mathematics Book
- Publication
- ReginaTagebücher
- Course
- CBSE Class 7
- Subject
- Mathmatics
Percentage
Introduction to percentage
Percentages are essentially fractions where the denominator is 100. To show that a number is a percent, we use the percent symbol (%) beside the number. For example, if you got 75 questions right out of 100 on a test (75/100), you would have scored 75%.
Conversion methods of percentage
Conversion of per cent into fraction
To convert a per cent into a fraction, divide it by 100 and remove the "%" sign.
![]()
Example:
(i) 37% = 37100
(ii) 22% = 22100
Note: Per cent is a fraction with a denominator of 100, and the numerator of this fraction is called Rate per cent.
2. Conversion of fraction into per cent
To convert any fraction to per cent, multiply it by 100 and put the per cent sign(%).
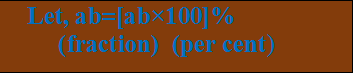
Example:
210=[210⋅100]% = 20%
Conversion of percentage into fraction
To convert the per cent into a ratio, change it to a fraction by dividing it by 100 and removing the per cent(%) sign. Finally, reduce the obtained fraction to the simplest form.
Conversion of ratio into per cent
We can convert the ratio into a percentage using the following method.
Example:
(i) a:b
=ab=[ab×100]%
Conversion of per cent into decimal
To convert the per cent to decimal, first change it to a fraction by dividing it by 1000 and remove the % sign. Then put the decimal point accordingly.
Conversion of decimal into a per cent
To convert decimal into a per cent, change it to fraction to remove decimal and then multiply it by 100 and put the % sign.
Theoretical explanation about finding a percentage
Finding a percentage of a given number:
To find the percentage of a given number, multiply the number by the require percent.
Let the number =x
Require percent =p%
Percentage of given number =p% of x
= p100 × x
Finding the original number from its percent:
Let original number =x
Require percent =p%
Obtained percentage =y
Now p% of x=y
p100×x =y
x= yp×100
![]()
Finding how much percent one quantity is of another quantity:
To find what percent of one quantity is of the other quantity if two quantities are given, we proceed as:

Percentage: Important points to remember


 Param Publication
Param Publication
 ReginaTagebücher
ReginaTagebücher
