- Books Name
- CBSE Class 7 Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 7
- Subject
- Mathmatics
Eulers Formula
The number of faces, edges and vertices of prism and pyramids are connected by the formula :
![]()
where V, F and E stand for the number of vertex , face and edge. This formula is known as Euler’s formula.
Cuboid : 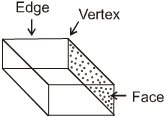
A cuboid has
(i) 6 rectangular faces
(ii) 12 edges
(iii) 8 vertices.
Let F, E and V denote respectively the number of faces, edges and vertices of a cuboid.
Then, F – E + V = 6 – 12 + 8 = 2.
Cube (Square prism) : 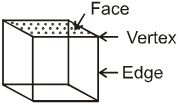
A cube has
(i) 6 square faces
(ii) 12 edges
(iii) 8 vertices
Here, F = 6, E = 12 and V = 8
∴ F – E + V = 6 – 12 + 8 = 2.
Triangular Pyramid : A triangular pyramid (Tetrahedron) shown in fig. has : (i) 4 faces 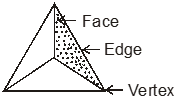
(ii) 6 edges
(iii) 4 vertices
Here, F = 4, E = 6 and V = 4
∴ F – E + V = 4 – 6 + 4 = 2
Illustration 1
A polyhedron has 20 edges and 10 vertices. How many faces does the polyhedron have ?
Solution
Here, E = 20, V = 10
V + F – E = 2
⇒ 10 + F – 20 = 2
⇒ F = 2 – 10 + 20 = 12
Hence, the polyhedron has 12 faces.
Illustration 2
Using Euler’s formula find the unknown.
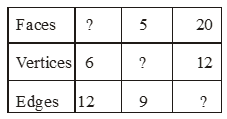
Solution
We know that using Euler’s formula
F + V – E = 2
(a) F + 6 – 12 = 2
or F – 6 = 2 or F = 8
Thus number of faces = 8
(b) 5 + V – 9 = 2
Thus number of vertices = 6
(c) 2 + 12 – E = 2
or 32 – 2 = E or 30 = E
Thus number of edges = 30
Illustration 3
Can a polyhedron have 10 faces, 20 edges and 15 vertices ?
Solution
The given data will be of a polyhedron, if it satisfies the Euler’s formula.
i.e., V + F – E = 2
Here V = 15, F = 10 and E = 20
Putting in L.H.S.
15 + 10 – 20 = 5 ≠ RHS
LHS ≠ RHS
Hence given vertices, faces and edges can’t be that of a polyhedron.

 Param Publication
Param Publication
