- Books Name
- CBSE Class 7 Mathematics Book
- Publication
- Param Publication
- Course
- CBSE Class 7
- Subject
- Mathmatics
V. RHS Congruency Criterion : (Right Angle-Hypotenuse-Side)
If the hypotenuse and one side of a right-angled triangle are equal to the hypotenuse and one side of another right-angled triangle, then the two triangles are congruent by RHS congruence criterion.
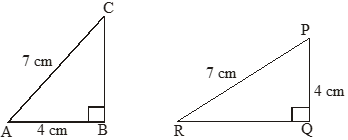

Note: Two triangles with equal corresponding angles need not be congruent. In such a correspondence, one of them can be an enlarged copy of other (They would be congruent only if they are exact copies of one another)
Special Properties of Isosceles and Equilateral Triangles :
1. The angles opposite to equal sides in an isosceles triangles are equal.
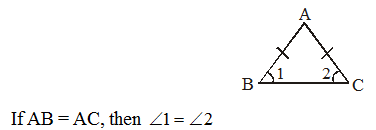
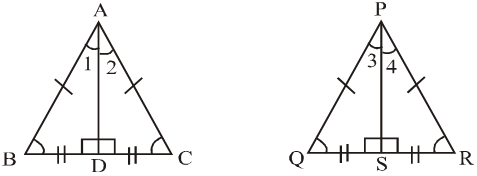
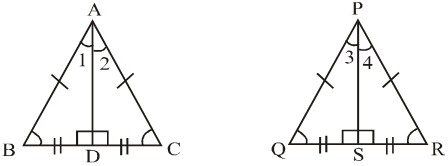
2. In an isosceles and an equilateral triangle the perpendicular drawn from the vertex to base bisects both the verticle angle and base.
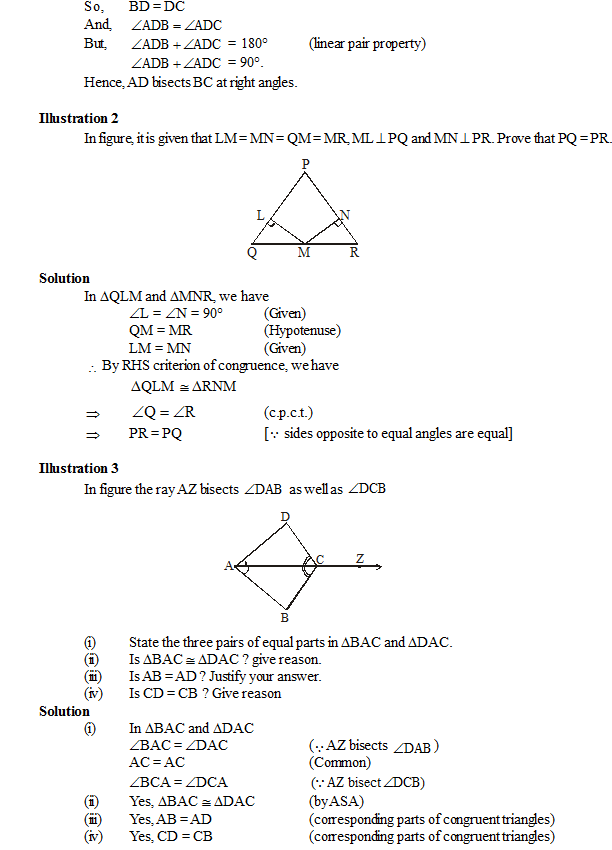
(a) ABC is an Isosceles Triangle in which AB = AC
(b) PQR is and Equilateral Triangle, in which PQ = RQ = PR.


 Param Publication
Param Publication
