Chapter 7: Congruence of Triangles

Chapter 7

Congruence of Triangles

Real-life examples of congruent objects

There are infinite examples of congruent objects which we see or observe in our daily life. A simple example is a pack of biscuits with all biscuits of the same size and shape if they are not broken. We can say all the biscuits are congruent.
A few more examples of congruency are:

• Earrings of the same set.
• Cigarettes in a pack.
• Wheels of a bicycle.
• Pages of a particular book.
• Your little fingers of both hands. Other fingers and thumbs are also congruent. Many of your body organs, like kidneys and lungs, are congruent. Even if a body is cut vertically from the center into two halves, both halves are congruent.

SSS Congruence

Congruence of triangles: Two triangles are said to be congruent if all three corresponding sides are equal and all the three corresponding angles are equal in measure. These triangles can be slides, rotated, flipped and turned to be looked identical. If repositioned, they coincide with each other. The symbol of congruence is’ ≅’.
The meaning of congruence in Maths is when two figures are similar to each other based on their shape and size. 
Congruence is the term used to define an object and its mirror image. Two objects or shapes are said to be congruent if they superimpose on each other.
The meaning of congruent in Maths is addressed to those figures and shapes that can be repositioned or flipped to coincide with the other shapes. These shapes can be reflected to coincide with similar shapes.
Congruent Triangles
A closed polygon made of three line segments forming three angles is known as a Triangle.
Two triangles are said to be congruent if their sides have the same length and angles have same measure. Thus, two triangles can be superimposed side to side and angle to angle.

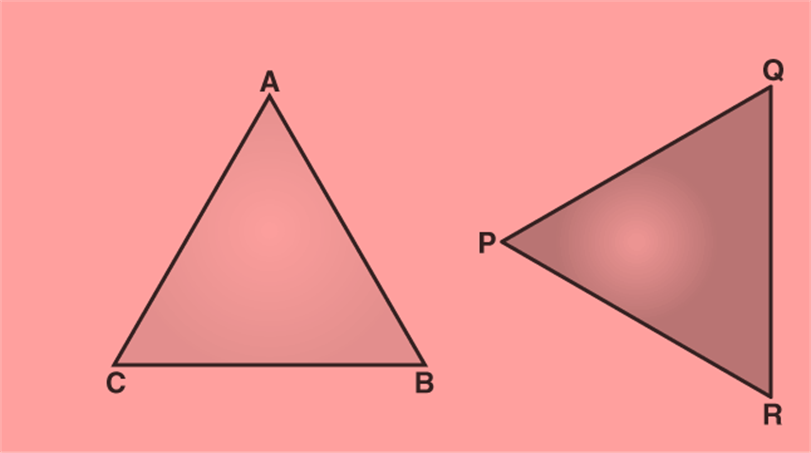
In the above figure, Δ ABC and Δ PQR are congruent triangles. This means,
Vertices:  A and P, B and Q, and C and R are the same.
Sides:  AB=PQ, QR= BC and AC=PR;
Angles:  ∠A = ∠P, ∠B = ∠Q, and ∠C = ∠R.

SSS Congruence Rule (Side – Side – Side)
The triangles are said to be congruent if all the three sides of one triangle are equal to the three corresponding sides of another triangle

Example :

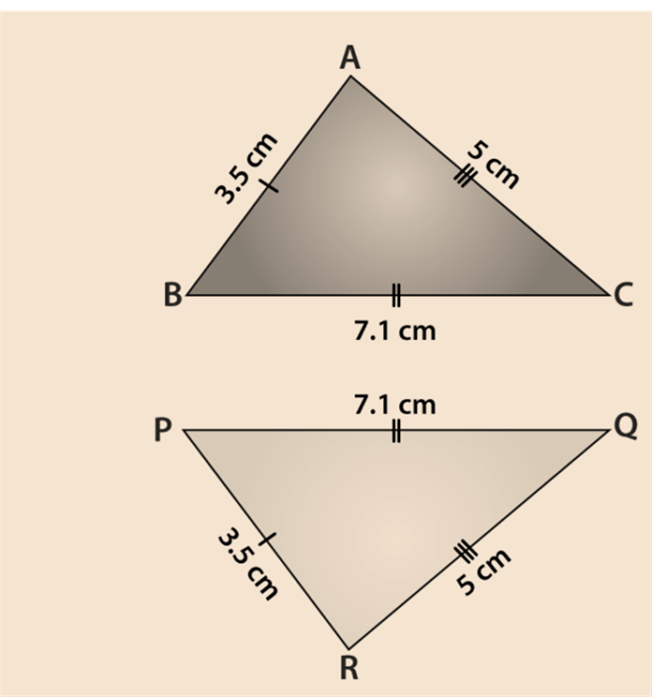
In the given triangles ABC and PQR, AB = 3.5 cm, BC = 7.1 cm, AC = 5 cm, PQ = 7.1 cm, QR = 5 cm and PR = 3.5 cm. Examine whether the given two triangles are congruent or not. If yes, then write the congruence relation in symbolic form.

Solution :

Given : AB = PR = 3.5 cm
BC = PQ = 7.1 cm and
AC = QR = 5 cm
This shows that all the sides of one triangle are equal to all sides of the other triangle. By using SSS congruence rule, the two triangles are congruent. From the three equality relations, we can write it as 

 A↔R, B↔P, C↔Q
So, the congruence of triangles in symbolic form is ∆ABC ≅ ∆RPQ

 

 

SAS Congruence

SAS Congruence Rule( Side – Angle – Side )
The triangles are said to be congruent if the correspondence, two sides and the angle included between them of a triangle are equal to two corresponding sides and the angle included between them of another triangle.

Example :
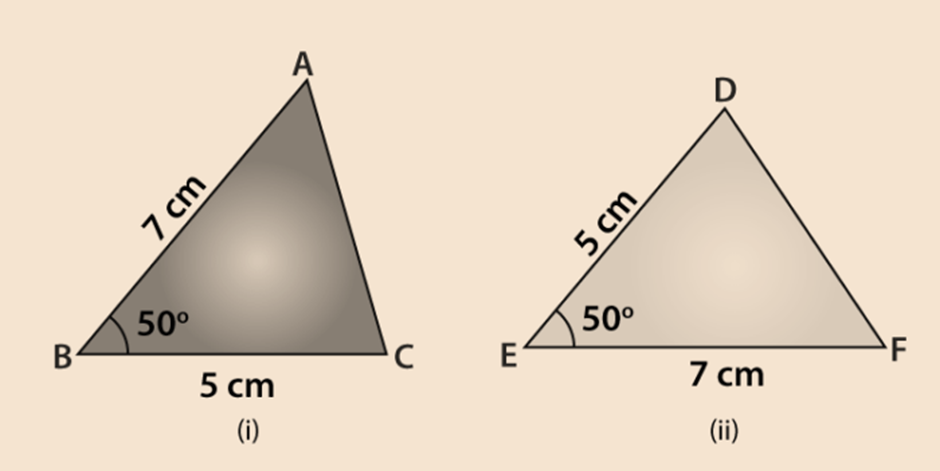
The measurements of some parts of two triangles are given below. Check whether the two triangles are congruent or not, using SAS congruence rule. Write it in symbolic form, if the triangles are congruent.
 For ∆ ABC, AB = 7 cm, BC = 5 cm, ∠B = 50° and for ∆ DEF, DE = 5 cm, EF = 7 cm, ∠E = 50°

Solution :

Given: AB = EF = 7 cm,

BC = DE = 5 cm and

∠B =∠E = 50°

Also,

By using SAS congruence rule, it can be written as

∆ABC ≅ ∆FED

A↔F, B↔E, C↔D

ASA Congruence

 

ASA Congruence Rule (Angle – Side – Angle )

The triangles are said to be congruent if two angles and the included side of a triangle are equal to two corresponding angles and the included side of another triangle.

Example :

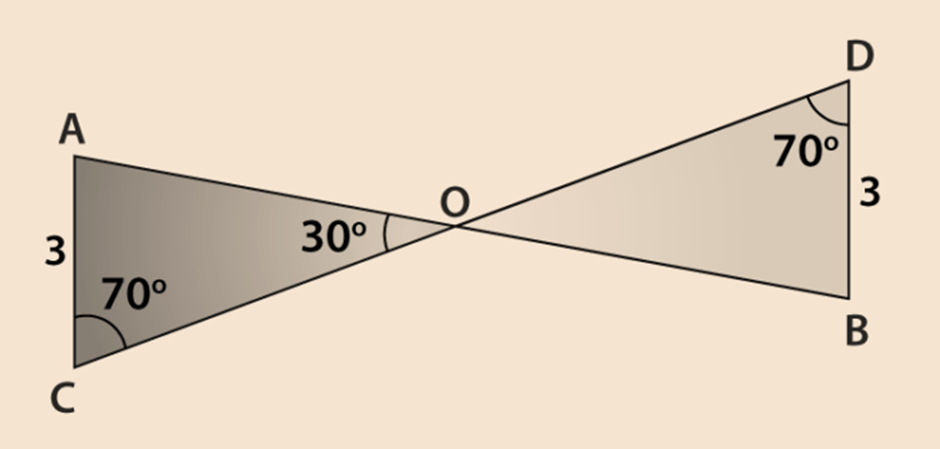
Conclude that ∆AOC ≅ ∆BOD, using ASA congruence rule from the given figure.

Solution :

Consider the two triangles AOC and BOD,
Given that ∠C = ∠D =70°
Also, note that  ∠AOC = ∠BOD = 30° Which are vertically opposite angles
So, we can write that the angle A of triangle AOC
∆AOC = 180° – (70° + 30°) = 80° (By angle sum property of a triangle)
Similarly, for ∠B of ∆BOD = 180° – (70° + 30°) = 80°
So, we have ∠A = ∠B, AC = BD and ∠C = ∠D
Now, the side AC is between ∠A and ∠C and the side BD is between ∠B and ∠D.
So, by using ASA congruence rule, it is written as
∆AOC ≅ ∆BOD.

RHS Congruence

The triangles are said to be congruent, then the hypotenuse and one side of a right-angled triangle are respectively equal to the hypotenuse and one side of another right-angled triangle.

Example :

Some parts of two triangles measurements are given below. Using RHS congruence rule, examine whether the given two triangles are congruent or not. In case, if the triangles are congruent write the result in a symbolic form. For ∆ABC and ∆PQR, the measurements are given below. For triangle ABC, ∠B = 90°, AC = 8 cm, AB = 3 cm and triangle PQR, ∠P = 90°, PR = 3 cm, QR = 8 cm.

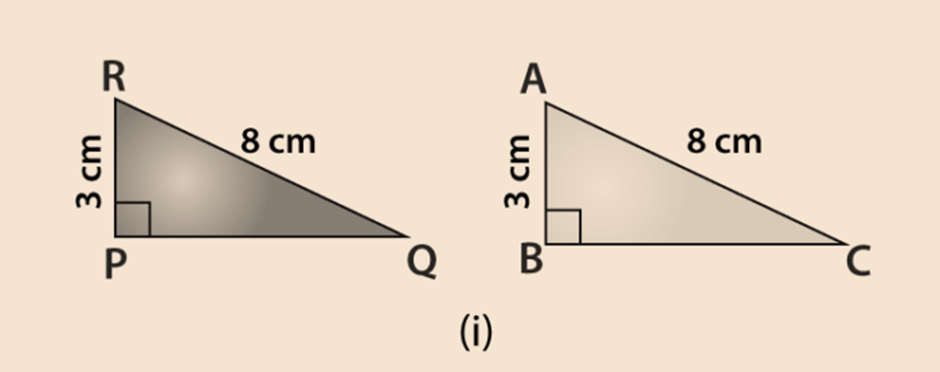
Solution :

Given : ∠B = ∠P = 90^o,
Hypotenuse side AC = RQ = 8 cm and
side AB = RP = 3 cm
So, by RHS Congruence rule, the symbolic form of the congruent triangle is written as
∆ABC ≅ ∆RPQ

 Example : In the following figure, AB = BC and AD = CD. Show that BD bisects AC at right angles.

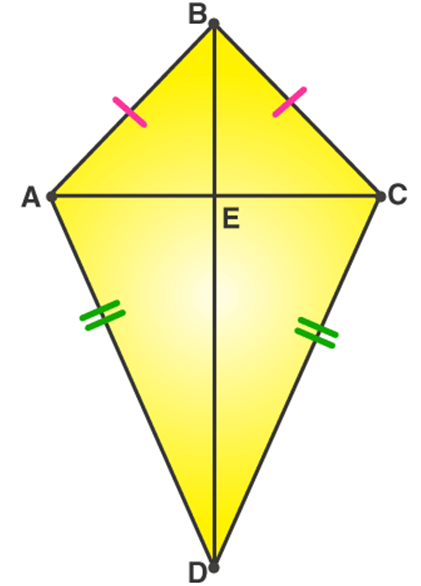
Solution: We are required to prove ∠BEA = ∠BEC = 90° and AE = EC.Consider ∆ABD and ∆CBD,AB = BC                                                
(Given)AD = CD                                       (Given)BD = BD                                                
                                                  (Common)Therefore, ∆ABD ≅ ∆CBD      (By SSS congruency)∠ABD = ∠CBD             (CPCTC)

Now, consider ∆ABE and ∆CBE,

AB = BC                                                (Given)

∠ABD = ∠CBD                                      (Proved above)

BE = BE                                                  (Common)

Therefore, ∆ABE≅ ∆CBE                      (By SAS congruency)

∠BEA = ∠BEC                                       (CPCTC)

And ∠BEA +∠BEC = 180°                     (Linear pair)

2∠BEA = 180°                                        (∠BEA = ∠BEC)

∠BEA = 180°/2 = 90° = ∠BEC

AE = EC                                                (CPCTC)

Hence, BD is a perpendicular bisector of AC.

In a Δ ABC, if AB = AC and ∠ B = 70°, find ∠ A.

Solution: Given: In a Δ ABC, AB = AC and ∠B = 70°

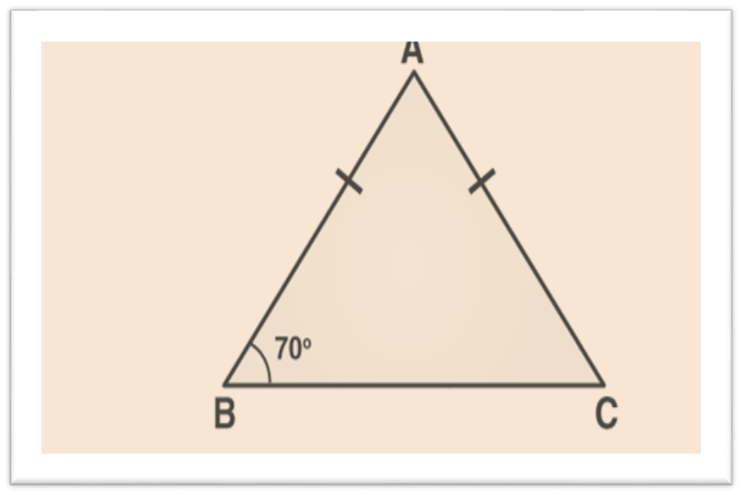
∠ B = ∠ C [Angles opposite to equal sides of a triangle are equal]

Therefore, ∠ B = ∠ C = 70°

Sum of angles in a triangle = 180°

∠ A + ∠ B + ∠ C = 180°

∠ A + 70° + 70° = 180°

∠ A = 180° – 140°

∠ A = 40°