Chapter 12: Algebraic Expressions

Various definitions and concepts
    Literals : The letters which are used to represent numbers are called literal numbers or literals. In 2xy, x & y are the literals.
    Literal numbers obey all the rules (and signs) of addition, subtraction, multiplication and division of numbers along with the properties of these operations. a × b = ab, 2 × a = 2a, 1 × a = a, x × 3 = 3x and a × a × a × ......× 15 times = a¹⁵. 
    In a⁵, 5 is called the index or exponent and a is called the base.

    Constant :  A term of the expression having no literal factor is called a constant term.

    (i)     In the binomial expression 5x + 7, the constant term is 7. In short, a symbol having a fixed numerical value is called a constant.

Variable : A symbol which takes various numerical values is called a variable.

Algebraic expression : A combination of constants and variables connected by the signs of fundamental operations of addition, subtraction, multiplication and division is called an algebraic expression.

 Types of algebraic expressions
 An algebraic expression is called a monomial, a binomial, a trinomial, a quadrinomial according as it contains one term, two terms, three terms and four terms respectively. 

Like terms : The terms having the same literal factors are called like or similar terms.
In the algebraic expression 12a² – 15b² + b² –17a² + 8ab + 9, we have, 12a² and –17a² as like terms and also – 15b² and b² are like terms. 

Unlike terms :  The terms not having same literal factors are called unlike or dissimilar terms.

In the algebraic expression 3p²q + 5pq² – 7pq – 9qp², 5pq² and –7pq are unlike terms.

Polynomial
    A polynomial is an algebraic expression with one or more terms.
    For example : 6x, x³ + 3x² + 9x + 7, 3x² – 4xy + 7y² etc. are all polynomials.   

Degree of polynomial
    The degree of a polynomial of one variable is the highest power of the variable in the given polynomial. For example P(x) = 2x³ + 3x² – 6x + 4. The highest power of x in all terms of polynomial is 3. 
    Hence, the degree of the polynomial is 3.  
    We can classify polynomial according to its degree.
    (i)     Constant polynomial : Polynomial having degree zero is known as constant polynomial. 

(ii)     Linear polynomial : Polynomial having degree one is known as linear polynomial. 
        For ex : 2x – 5, x + 3.
(iii)   Quadratic polynomial : Polynomial having degree two is known as quadratic polynomial. 
        For ex :  x² + 1, 7x², x² + 2x – 1.
(iv)   Cubic polynomial : Polynomial having degree three is known as cubic polynomial. 
        For ex :  7x³ + 5x² + 1, x³ – x + 1.
(v)   Biquadratic polynomial : Polynomial having degree four is known as biquadratic polynomial. 
        For ex : x⁴ + 1, x⁴ + x² + 1.

Factors : Each term in an algebraic expression is a product of one or more number(s) and/or literal number(s).

These number(s) and/or literal number(s) are known as the factors of that term.
    (i)     In the binomial 8ab + 3c, 8ab and 3c are two terms. In the term 8ab, 8, a and b are its factors. Clearly, number 8 is the numerical factor, and a and b are literal factors.
    (ii)    In the binomial expression – ab – 5, the term – ab has – 1 as the numerical factor while a and b are literal factors.

Coefficient : In a term of an algebraic expression any of the factors with the sign of the term is called the coefficient of the product of the factors.
Consider the term – 5ab in the binomial – 5ab + 7. The coefficient of a in the term – 5ab is – 5b, the coefficient of b is – 5a and the coefficient of ab is – 5.

Addition or subtraction of like terms
     The sum or difference of several like terms is another like term whose coefficient is the sum or difference of those like terms.
    Illustration 1 
        Add the following : 3xy, 10xy and 5xy.
    Solution
        The sum of the numerical coefficients of the given like terms is 3 + 10 + 5 = 18.
        Hence, 3xy + 10xy + 5xy = 18xy.

    Illustration  2
         Add the following : – 2p²q,  – 9p²q,  – 14p²q and  – 5p²q.
    Solution
        The sum of the numerical coefficients (without negative sign) is : 2 + 9 + 14 + 5 = 30
        Hence, –2p²q – 9p²q – 14p²q – 5p²q = – 30p²q.
 
    Illustration  3
         Add the following : 3x + y + 4 and 4x + 3y + 7.
    Solution    
        Horizontal Method
            (3x + y + 4) + (4x + 3y + 7)
        =     (3x + 4x) + (y + 3y) + (4 + 7)
        =     (3 + 4)x + (1 + 3)y + (4 + 7)
        =     7x + 4y + 11

                 Or

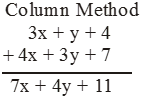
Illustration 4
         Add the following : 3x + 4y + 5z and 2x – 3y – 4z.
 Solution
        Horizontal Method
            (3x + 4y + 5z) + (2x – 3y – 4z)
        =     (3x + 2x) + (4y – 3y) + (5z – 4z)
        =     (3 + 2)x + (4 – 3)y + (5 – 4)z
        =     5x + y + z

                 Or

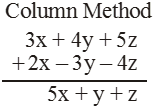
NOTE : To subtract an expression from another, we change the sign (from' + ' to ' – ' and from' – ' to ' + ') of each term of the expression to be subtracted and then add the two expressions.

Illustration 5 
        Subtract :
         (i) 3p from 7p        (ii) – 8x from 9x    (iii) – 3a from 7a    (iv) – 9b from – 2b
 Solution
        (i)     7p – 3p = (7 – 3)p = 4p
        (ii)     9x – (–8x) = 9x + 8x =(9 + 8) x = 17x
        (iii)     7a – (–3a) = 7a + 3a = (7 + 3)a = 10a
        (iv)     – 2b – (– 9b) = – 2b + 9b = (– 2 + 9)b = 7b

Illustration 6 
        What should be subtracted from 2p³ – 4p² + 5p – 6 to obtain p² – 2p + 1 ?
 Solution
        Let X denote the required expression. 
        Then, (2p³ – 4p² + 5p – 6) – X = p² – 2p + 1    
        Hence, required expression          
        X = (2p3 – 4p2 + 5p – 6) – (p2 – 2p + 1)
        X = 2p³ – 4p² + 5p – 6 – p² + 2p – 1
        X = 2p³ – 4p² – p² + 5p + 2p – 7
        X = 2p³ – 5p² + 7p – 7

NOTE : When a grouping symbol preceded by, ‘–' sign is removed or inserted, then the sign of each term of the corresponding expression is changed (from '+' to '–' and from '–'  to  '+'). 

Illustration 7 
        Simplify : 2x – {4y – (3x – 5y)}.
 Solution
        We first remove the innermost grouping symbol ( ) and then braces { }.
        Thus, we have
            2x – {4y – (3x – 5y)}
            = 2x – {4y – 3x + 5y}        [Removing ( )]
            = 2x – {9y – 3x} 
            = 2x – 9y + 3x
            = 2x + 3x – 9y
            = 5x – 9y.

Illustration 8
        Simplify and find the value of the following expression when a = 2 and b = 3 :
        4(a² + b² + 2ab) – [4(a² + b² – 2ab) – {– b³ + 4(a – 3)}]    
  Solution
        Proceeding outward from the innermost bracket,
        4(a² + b² + 2ab) – [4(a² + b² – 2ab) – {– b³ + 4(a – 3)}]
            = 4(a² + b² + 2ab) – [4(a² + b² – 2ab) – {– b³ + 4a – 12}]
            = 4a² + 4b² + 8ab – [4a² + 4b² – 8ab + b³ – 4a + 12]
            = 4a² + 4b² + 8ab – 4a² – 4b² + 8ab – b³ + 4a – 12
            = 4a² – 4a² + 4b² – 4b² + 8ab + 8ab – b³ + 4a – 12
            =  (4 – 4)a² + (4 – 4)b² + (8 + 8)ab – b³ + 4a – 12
            = 16ab – b³ +  4a – 12
        Thus va    lue of this expression for a = 2 and b = 3 is :
            16 × 2 × 3 – (3)³ + 4 × 2 – 12  = 96 – 27 + 8 – 12 = 65.

Division of algebraic expressions
    Division is the inverse process of multiplication.
    When we divide one expression by another, we find a third expression which when multiplied by the second gives the first , i.e., if a ÷ b = x then a = bx. In a ÷ b = x, ‘a’ is called the Dividend, ‘b’ the Divisor and ‘x’ is called the Quotient.
    Rules of Signs in Division :
    (i)     When the dividend and the divisor have the same signs, the quotient has the plus sign.
    (ii)     When the dividend and the divisor have opposite signs, the quotient has the negative sign. 

Division of a Monomial by another Monomial :

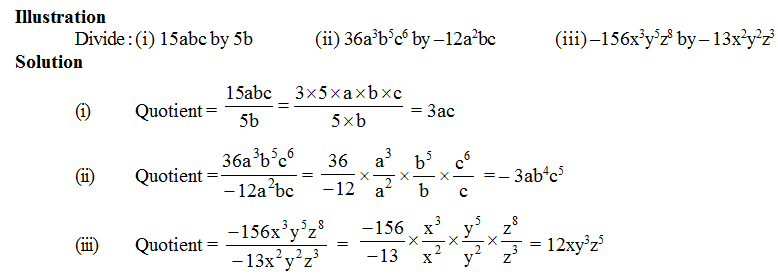
Division of a Polynomial by a Monomial :
       Divide each term of the polynomial by the monomial and then write the resulting quotients.

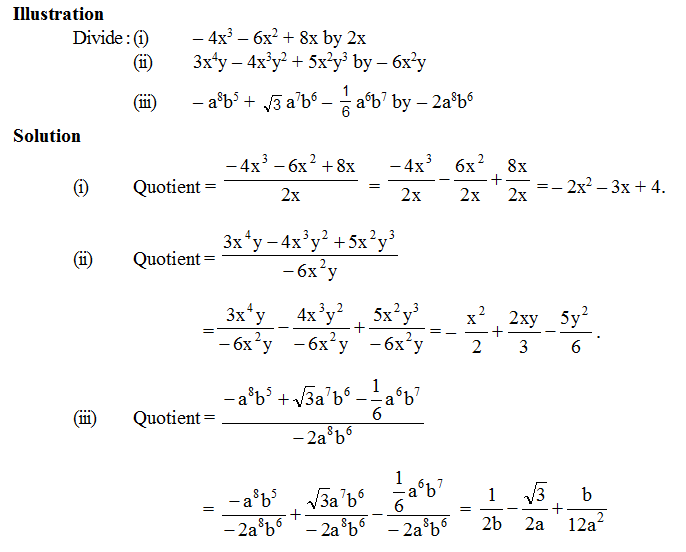
Algebraic identities
    An identity is an equality, which is true for all values of the variables. The following three identities are very important. 

    Identity 1 : (a + b)² = a² + 2ab + b²
    Proof : we have : 
        (a + b)²       = (a + b) (a + b)
              = a (a + b) + b(a + b)
              = a² + ab + ba + b²
              = a² + 2ab + b²                            [Since ba = ab]
   ∴    (a + b)²  = a2 + 2ab + b².  

    Identity 2 : (a – b)² = a² – 2ab + b². 
    Proof : we have 
        (a – b)²     = (a – b) (a – b)
            = a(a – b) – b(a – b) 
            = a² – ab – ba + b² 
            = a² – ab – ab + b²                  [Since ba = ab]
            = a² – 2ab + b².
            = (a² – 2ab + b²) 

Identity 3 : (a + b)(a – b) = a² – b²
    Proof     We have : 
        (a + b) (a – b) = a (a – b) + b(a – b)
                       = a² – ab + ba – b²
                       = a²  – b²                            [Since ba = ab]
   ∴     (a + b)(a–b)    = a² – b².

Applications of the above identities :

    Illustration 
        Find each of the following products : 
         (i) (3x +2y) (3x +2y)             (ii) (4x² + 5) (4x² + 5) 
         (iii) (2x – 5y)²                      (iv) (3x2 +2y²) (3x² – 2y²) 

Solution       
        (i)     (3x +2y)(3x +2y) = (3x +2y)² 
                                           = (3x)² + (2y)² + 2 (3x) (2y)       [Using (a + b)² = a² + b² + 2ab]
                                           = 9x² +4y² + 12xy.     
        ∴     (3x + 2y) (3x + 2y) = 9x² + 4y² + 12xy. 

        (ii)     (4x² + 5)(4x² + 5) = (4x² + 5)² 
                                             = (4x²)² + 5² + 2 (4x²) 5     [Using (a + b)² = a² + b² + 2ab] 

                                            = 16x4 +25 + 40x2. 

        (iiii)     (2x – 5y)² = (2x)² + (5y)² – 2 (2x) (5y)        [Using (a – b)² = a² + b² – 2ab] 
                    = 4x² + 25y² – 20xy. 

        (iv)     (3x² + 2y² )(3x² – 2y²) = (3x²)² – (2y²)²     [∴ (a + b) (a – b) = (a² – b²)] 
                                  = (9x⁴ – 4y⁴).

Multiplication of algebraic expressions
    Following rules of signs and the laws of exponents used in multiplication.

1.     Rules of signs in multiplication : 
    The product of two factors with like signs is positive, and the product of two factors with unlike signs is negative. Thus if a and b are two positive numbers then 

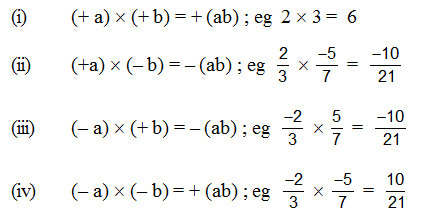
2.    Laws of exponents in multiplication 
       Law of exponents in multiplication is given as :
        a^m x aⁿ  = a^m+n  x e.g. x⁵ x x² = x^{5 + 2} = x⁷ 

Multiplication of a Monomial by a Monomial : 

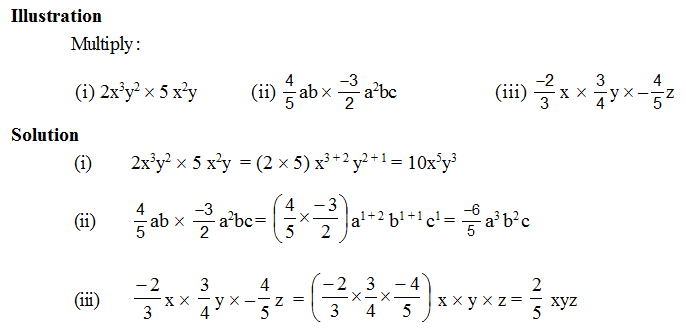
      Thus in multiplication of algebraic expression : 
    (i)     Write the product of the numerical coefficients. 
    (ii)     Write all the different letters occurring in the algebraic expressions giving to each letter an exponent (power) equal to the sum of all the exponents of that letter in the given expressions. 
    (iii)     The sign of the product is minus if there is an odd number of negative factors and plus if there is an even number of negative factors.

Multiplication of a Binomial by a Monomial : 
    In order to multiply a binomial by a monomial use the following rule : 
    a x (b + c)  = a x b + a x c. 

    Illustration 
        Multiply  : (i)   3x² + 4xy by 2x         (ii) –4a [a + 3b]    (iii) – 4a [a – 3b]
    Solution    
        (i)     2x [3x² + 4xy] = 2x x 3x² + 2x x 4xy  = 6x³ + 8x²y 
        (ii)     – 4a [a + 3b]  = – 4a x a  – 4a x 3b = – 4a² – 12ab 
        (iii)     – 4a [a – 3b] = – 4a ´ a – 4a ´ (–3b) = – 4a² + 12 ab. 

Multiplication of a Binomial by a Binomial : 
    In multiplication of a binomial by binomial we will use the law of multiplication of a binomial by a monomial twice. 
    Illustration     
        (i)     (a + b) (c + d) 
        (ii)     (2x² + 3y) (3x² – 2y)
    Solution
         (i)     (a + b) (c + d)     = a (c + d) + b (c + d)
                      = a x c + a x d + b x c + b x d
                     = ac + ad + bc + bd 

        (ii)     (2x² + 3y) (3x² – 2y) 
                    = 2x² (3x² – 2y) + 3y (3x² – 2y)
                    = 2x² x 3x² + 2x² x (– 2y) + 3y x 3x² + 3y x (–2y) 
                    = 6x⁴ – 4x²y + 9x²y – 6y²