2. Expressions and Equations

Variable
In the above example, we found a rule to give the number of matchsticks required to make a pattern of Ls. The rule was: Number of matchsticks required = 2n Here, n is the number of Ls in the pattern, and n takes values 1, 2, 3, 4,.... 
Let us look at Table 1 once again. In the table, the value of n goes on changing (increasing). As a result, the number of matchsticks required also goes on changing (increasing). 
n is an example of a variable. Its value is not fixed; it can take any value 1, 2, 3, 4, ... . We wrote the rule for the number of matchsticks required using the variable n.
The word ‘variable’ means something that can vary, i.e. change. The value of a variable is not fixed. 
It can take different values.
Examples of variables : We have used the letter n to show a variable. There is nothing special 
about n, any letter can be used. One may use any letter as m, l, p, x, y, z etc. to show a variable. Remember, a variable is a number which does not have a fixed value. For example, the number 5 or the number 100 or any other given number is not a variable. They have fixed values. Similarly, the number of angles of a triangle has a fixed value i.e. 3. It is not a variable. The number of corners of a quadrilateral (4) is fixed; it is also not a variable. But n in the examples we have looked is a variable. It takes on various values 1, 2, 3, 4, ... .    

Let us take other example of variable : Raju and Balu are brothers. Balu is younger than Raju by 3 years. When Raju is 12 years old, Balu is 9 years old. When Raju is 15 years old, Balu is 12 years old. We do not know Raju’s age exactly. It may have any value. Let x denote Raju’s age in years, x is a variable. If Raju’s age in years is x, then Balu’s age in years is (x – 3). The expression (x – 3) is read as x minus three. As you would expect, when x is 12, (x – 3) is 9 and when x is 15, (x – 3) is 12.

Expressions with Variables
To form expressions we use all the four number operations of addition, subtraction, multiplication and division. For example, to form (2 × 10) + 3, we have multiplied 2 by 10 and then added 3 to the product. Expressions can be formed from variables too. In fact, we already have seen expressions with variables, for example: 2n, 5m, x + 10, x – 3 etc. These expressions with variables are obtained by operations of addition, subtraction, multiplication and division on variables. For example, the expression 2n is formed by multiplying the variable n by 2; the expression (x + 10) is formed by adding 10 to the variable x and so on.
One important point must be noted regarding the expressions containing variables. A number expression like (4 × 3) + 5 can be immediately evaluated as (4 × 3) + 5 = 12 + 5 = 17. But an expression like 
(4x + 5), which contains the variable x, cannot be evaluated. Only if x is given some value, an expression like (4x + 5) can be evaluated. For example, when x = 3, 4x + 5 = (4 × 3) + 5 = 17 as found above.

Ex.1     Give expressions for the following cases.
(a)     Rita scores x marks in Maths and 46 marks in English. What is her total score in Maths and English. 
 (b)     The difference of x and 9 where x > 9.
(c)     The product of a and b  added to the difference of a and b (a > b).
(d)     One-half of a multiplied by the sum of x and y.

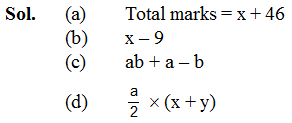
Ex.2 Ali is x years old. Express the following in algebraic form : 
(a)     4 times Ali's age 3 years hence. 
(b)      The present age of Ali's aunt who is four times as old as Ali will be 5 years from today. 
(c)     The present age of Ali's father who is 5 times as old as Ali was 3 years ago. 

Sol.   (a)     Ali's age 3 years hence = (x + 3) years 4 times Ali's age 3 years hence = 4(x + 3) years. 
(b)      Ali's age after 5 years = (x + 5) years. Ali's aunt age = 4 (x + 5) years   
(c)     Ali's age before 3 years = (x – 3) years. Ali's father age = 5(x – 3) years