Chapter 3: Playing With Numbers

Factors
Any number which is an exact divisor of  a given number is called a factor of the given number.
    For example factor of 6 are 1,2,3 and 6
    Important results :
    (a)     1 is a factor of every number.
    (b)     Every number is a factor of itself.
    (c)     Every factor of a number is always equal to or less than the number.
    (d)     Every number has a finite number of factors.

Some problems on HCF and LCM
 Ex.     Find the greatest number which divides 43 and 91 leaving remainder 7 in each caes.
 Sol.     It is given that the required number when divides 43 and 91, the renainder is 7 in each case . This means that 43 – 7 = 36  and 91– 7  = 84   are completely divisible by required number . 
Also, the required number is the greatest number satisfying the above property .
       ∴      It is the HCF of 36 and 84.
            36 = 2 × 2 × 3 × 3 
            84 = 2 × 2 × 3 × 7 
       ∴    Required HCF = 2 × 2 × 3 = 12
        Hence, the required number  = 12

Ex.     Find the largest number that will divide 20, 57 and 85 leaving remainders 2, 3 and 4 respecitively.
Sol.   Clearly, the required number is the HCF of the number 20 – 2 = 18, 57 – 3 = 54 and 85 – 4 = 81.  
        18 = 2 × 3 × 3  
        54 = 2 × 3 × 3 × 3 
        81 = 3 × 3 × 3 × 3 
        ∴   Required HCF = 3 × 3 = 9
        Hence, the required number  = 9

Relationship between HCF and LCM 
Let us take two numbers, say 16 and 24.
The HCFof 16 and 24 is 8.
The LCM of 16 and 24 is 48.
Since 8 is factor of 48, so we can say that HCF of the numbers is a factor of their  LCM.
Product of HCF and LCM = 8 × 48 = 384
Product of Numbers = 16 x 24 = 384
So we can say that the product of two numbers is equal to the product of  their HCF and LCM.
Let a and b are two numbers then

a x b =  HCF × LCM 

Ex.     The HCF of two number is 29 and their LCM is 1160. If one of the number is 145,  find the other.
Sol.     We know that 
        Product of the number      = HCF × LCM
                x × 145 = 29 × 1160
                         
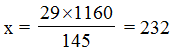
        ∴    Required number  = 232

Ex.     Find the least number which when divided by 6, 7, 8, 9 and 10 leaves reamainder 1.
Sol.     As the remainder is same
        Required number = LCM of divisors + Remainder
                                    = LCM (6, 7, 8, 9, 10) +1
                                    = 2520 + 1 = 2521

Ex.    Find the least number which when decreased by 7 is exactly divisible by 12, 16, 18, 21 and 28.
   
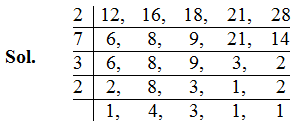
        LCM = 2 × 7 × 3 × 2 × 4 × 3 = 1008
        Required number = 1008 + 7 = 1015. 

Lowest Common Multiple
The Lowest Common Multiple (LCM) of two or more given numbers is the lowest (or smallest or least) of their common multiples.
Ex.:     Find the LCM of 24 and 90. 
Sol.:     The prime factorisations of 24 and 90 are:
            24 = 2 × 2 × 2 × 3; 90 = 2 × 3 × 3 × 5
        In these prime factorisations the maximum number of times the prime factor 2 occurs is three; this happens for 24. Similarly, the maximum number of times the prime factor 3 occurs is two; this happens for 90. The prime factor 5 occurs only once in 90.
Thus, LCM = (2 × 2 × 2) × (3 × 3) × 5 = 360

Highest Common Factor
The Highest Common Factor (HCF) of two or more given numbers is the highest (or greatest) of their common factors. 
It is also known as Greatest Common Divisor (GCD). 
The HCF of 20, 28 and 36 can also be found by prime factorisation of these numbers as follows:

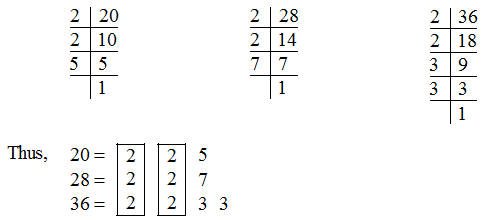
The common factor of 20, 28 and 36 is 2(occuring twice). Thus, HCF of 20, 28 and 36 is 2 × 2 = 4.

Prime Factorisation
When a number is expressed as a product of its factors we say that the number has been factorised. Thus, when we write 24 = 3×8, we say that 24 has been factorised. This is one of the factorisations of 24. The others are :

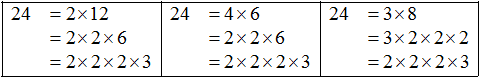
Such a factorisation of a number is called a prime factorisation.

Ex :     Find the prime factorisation of 980.
Sol.:     We proceed as follows:
We divide the number 980 by 2, 3, 5, 7 etc. in this order repeatedly so long as the quotient is divisible by that number.Thus, the prime factorisation of 980 is 2 × 2 × 5 × 7 × 7.

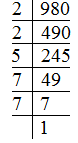
Some More Divisibility Rules
(i)    If a number is divisible by another number then it is divisible by each of the factors of that number.
         Ex.    18 is divisible by 9.  The factors of 9 is 3. 18 is also divisbile by 3.
(ii)    If a number is divisible by two co-prime numbers then it is divisible by their product also.
       Ex.    The number 80 is divisible by 4 and 5. It is also divisible by 4 × 5 = 20, and 4 and 5 are 
co-primes.
 Similarly, 60 is divisible by 3 and 5 which are co-primes. 60 is also divisible by 3 × 5 = 15.
(iii)     If two given numbers are divisible by a number, then their sum is also divisible by that number.
       Ex.    The numbers 16 and 20 are both divisible by 4. The number 16 + 20 = 36 is also divisible by 4. 
(iv)     If two given numbers are divisible by a number, then their difference is also divisible by that number.
      Ex.    The numbers 35 and 20 are both divisible by 5. Is their difference 35 – 20 = 15 also divisible by 5.

Common Factors 
    The factors of 4 are 1, 2 and 4.
    The factors of 18 are 1, 2, 3, 6, 9 and 18. The numbers 1 and 2 are the factors of both 4 and 18.
    They are the common factors of 4 and 18.
    Two numbers having only 1 as a common factor are called co-prime numbers. Thus, 4 and 15 are 
co-prime numbers.

Common Multiples
    The multiples of 4 are 4, 8, 12, 16, 20, 24, ... 
    The multiples of 6 are 6, 12, 18, 24, 30, 36, ...
   We observe that 12, 24, 36, ... are multiples of both 4 and 6.

They are called the common multiples of 4 and 6.
    Ex.    Find the common multiples of 3, 5 and 6.
    Sol.    Multiples of 3 are 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, ...
        Multiples of 5 are 5, 10, 15, 20, 25, 30, 35, ...
        Multiples of 6 are 6, 12, 18, 24, 30, ...
        Common multiples of 3, 5 and 6 are 30, 60, ...

DIVISIBILITY TEST
(a)     Divisibilit by 2 : A given number is divisible by 2, if its unit digit is any of 0, 2, 4, 6, 8 e.g. 4268134 is divisible by 2 while 311267429 is not divisible by 2. 

(b)    Divisibility by 3 : A number is divisible by 3, if sum of its digits is divisible by 3 e.g. 252771 is divisible by 3 as sum of its digits (2 + 5 + 2 + 7 + 7 + 1 = 24) is divisible by 3.

(c)    Divisibility by 4 : A number is divisibly by 4 if the last two digits of the number is divisible by 4 or the number ends with '00'. e.g. 213428 is divisible by 4 as last two digits is 28 which is divisible by 4. 1246800 is also divisible by 4 as the number ends with 00.

(d)    Divisibility by 5 : A number is divisible by 5 if its unit place digit is either 0 or 5.

(e)    Divisibility by 6 : A number is divisible by 6 if it is divisible by 2 and 3 both. e.g., 254784 is divisible by 6 because it is an even number and hence divisible by 2, also the sum of digits  i.e., 2 + 5 + 4 + 7 + 8 + 4 = 30 is divisible by 3. Hence the number is divisible by 6.

(f)    Divisibility by 8 : A given number is divisible by 8 if the number formed by last three digits of the number is divisible by 8 or the number ends with '000' e.g., 342840 is divisible by 8 because 840 is divisible by 8. 29342000 is also divisible by 8.

(g)    Divisibility by 9 : A number is divisible by 9 if the sum of digits of the number is divisible by 9. e.g. 284796 is divisible by 9 because sum of digits 2 + 8 + 4 + 7 + 9 + 6 = 36 is completely divisible by 9.

(h)    Divisibility by 10 : A number is divisible by 10 if the unit place digit of given number is '0' e.g., 21380, 3142900 are divisible by 10, whereas 214385, 329212, 46843 are not divisible by 10.

(i)    Divisibility by 11 : A number is divisible by 11 if the difference between the sum of the digits in the odd places and the sum of the digits in the even places is either O or completely divisible by 11. e.g., 6584919 is divisible by 11 because. (Sum of digits at odd places) – (Sum of digits at even places)
⇒     (6 + 8 + 9 + 9) – (5 + 4 + 1)
⇒     32 – 10 = 22, which is divisible by 11.

(j)    Divisibility by 12 : If a given number is divisible by both 3 and 4 then it is also divisible by 12 e.g., 16128 is divisible by both 3 and 4 and hence it is divisible by 12 also.

Types of Numbers
    (a)     Even Number : A number which is exactly divisible by 2 is called an even number.
        Examples of even numbers are : 0, 12, 34, 56, 78,....

    (b)     Odd Number : A number which is not exactly divisible by 2 is called an odd number.
        Examples of odd numbers are : 1, 13, 15, 25, 29,....

    (c)     Prime Numbers : A natural number greater than 1, which has no factors except 1 and itself is called a prime number.
        Examples of prime numbers are : 2, 3, 5, 11, 13, 17, ...

    (d)     Composite Numbers : A number is composite if it has at least one factor other than 1 and itself.
        Examples of composite numbers are : 4, 6, 8, 9,10, 12, 14,...
        Note :
        (i)     1 is neither prime nor composite.
        (ii)     Every natural number except 1 is, either a prime number or a composite number.
        (iii)     2 is the only prime number which is even. All other prime numbers are odd.

    (f)     Perfect Numbers : If the sum of all the factors of a number is twice the number, then number is called a perfect number. For example, 6 is a perfect number since the factors of 6 are 1, 2,3, 6 and their sum 1 + 2 + 3 + 6 = 2 × 6.

    (g)     Coprime Numbers : Two numbers are said to be coprime if they do not have a common factor other than 1.
        Examples of coprime numbers are : (8, 15); (5, 9); (2, 11)

        Note :
        (i)    Two prime numbers are always coprime.
        (ii)     Two coprime numbers need not be both prime numbers.

Multiples
    Just as 1,2,3, and 6 are factors of 6 , we say that 6 is multiple of 1,2,3, and 6.
    A number is a multiple of each of its factors 
    Important results :
    (a)     Every number is a multiple of itself.
    (b)     Every multiple of a number is equal to or greater than the number.
    (c)     Every number has as infinite number of multiples.