1.Reflection of Light by Spherical Mirrors
- Books Name
- Physics Book Part l and ll
- Publication
- Grow Career Publication
- Course
- CBSE Class 12
- Subject
- Physics
Chapter 9: Ray optic and optical instrument
Reflection of Light by Spherical Mirrors
Reflection of Light
When light is incident on a surface, it is sent back by the surface in the same medium through which it had come called as ‘reflection of light’ by the surface.
Laws of Reflection
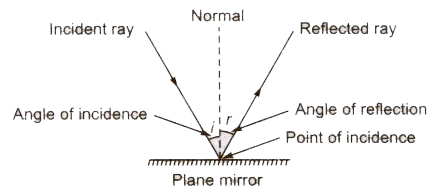
There are two laws of reflection.
- The incident ray, the reflected ray and the normal at the point of incidence all three lie in the same plane.
- The angle of incidence (i) is always equal to the angle of reflection .
Types of Reflection
- Regular Reflection When a parallel beam of reflected light rays is obtained for a parallel beam of incident light rays after reflection from a plane reflecting reflection is called regular reflection.
- Irregular or Diffused Reflection When a non-parallel beam of reflected light rays is obtained for a parallel beam of incident light rays after reflection from a surface, then such type of reflection is called irregular or diffused reflection.
Reflection of Spherical Mirror
- A spherical mirror is a part cut from a hollow sphere.
- The reflection at spherical mirror also takes place in accordance with the laws of reflection.
Sign Convention
All distances are measured from the pole of the mirror & the distances measured in the direction of the incident light is taken as positive.
(i) The distance measured against the direction of the incident light are taken as negative.
Focal Length of a Spherical Mirror
Distance between the focus and the pole of the mirror is called focal length of the mirror and is denote by f.
b) The focal length of a concave mirror is negative and that of a convex mirror is positive.
c) The focal length of a mirror (concave or convex) is equal to half of the radius of curvature of the mirror, i.e., f = .
Principal Axis of the Mirror: The straight line joining the pole and the centre of curvature of spherical mirror extended on both sides is called principal axis of the mirror.
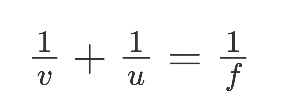
Mirror Formula:
Where u = distance of the object from the pole of mirror
V = distance of the image from the pole of mirror
F = focal length of the mirror
Where R is the radius of curvature of the mirror.
Magnification: It is defined as the ratio of the size of the image to that of the object.
Luminous Objects
The objects which emits its own light, are called luminous objects, e.g., sun, other stars, an oil lamp etc.
Non-Luminous Objects
The objects which do not emit its own light but become visible due to the reflection of light falling on them, are called non-luminous objects, e.g., moon, table, chair. Trees etc.
Ray of Light
A straight line drawn in the direction of propagation of light is called a ray of light.
Beam of Light A bundle of the adjacent light rays is called a beam of light.
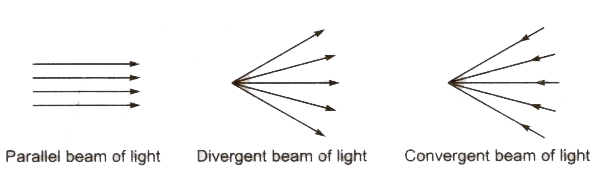
Image If light ray coming from an object meets or appear to meet at a point after reflection or refraction, then this point is called image of the object.
Real Image The image obtained by the real meeting of light rays, is called a real image.
Real image can be obtained on a screen. Real image is inverted.
Virtual Image The image obtained when light rays are not really meeting but appears to meet only, is called a virtual image.
Types of Reflection
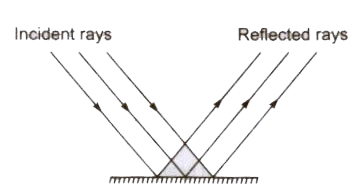
(i) Regular Reflection When a parallel beam of reflected light rays is obtained for a parallel beam of incident light rays after reflection from a plane reflecting reflection is called regular reflection.
(ii) Irregular or Diffused Reflection When a non-parallel beam of reflected light rays is obtained for a parallel beam of incident light rays after reflection from a surface, then such type of reflection is called irregular or diffused reflection.

Mirror
A smooth and highly polished reflecting surface is called a mirror.
(i) Plane Mirror A highly polished plane surface is called a plane mirror.
Spherical Mirror : A highly polished curved surface whose reflecting surface is a cut part of a hollows at glass sphere is called a spherical mirror. Spherical mirrors are of two types
- Concave Mirror A spherical mirror whose bent in surface is reflecting surface, is called a concave mirror.
- Convex Mirror A spherical mirror whose bulging out surface is reflecting surface, is called a convex mirror.
REFRACTION AT SPHERICAL SURFACES AND BY LENSES
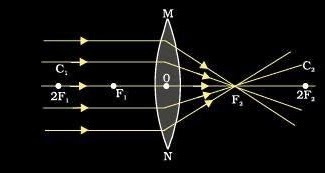
1. Focal length of a convex lens: The distance between the optical centre and principal focus of a lens is called focal length.Focal length of a lens depends on the refractive index of the glass and its curvature. In case of higher refractive index, focal length will be short.
A convex lens is also called converging lens as the parallel beam of light rays passing through it converges at a single point.
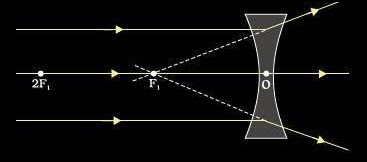
2. Focal length of concave lens:
The distance between optical centre and principal focus is called focal length of a concave lens.
Refraction at Spherical Surfaces
Consider refraction at a spherical interface between two transparent media. An infinitesimal part of a spherical surface can be regarded as planar and the same laws of refraction can be applied at every point on the surface.
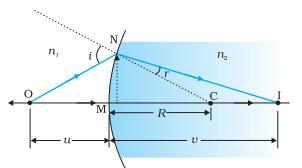
The rays are incident from a medium of refractive index n1, to another of refractive index n2.
Assuming the aperture (or the lateral size) of the surface to be small compared to other distances involved, so that small angle approximation can be made.
Consider NM will be taken to be nearly equal to the length of the perpendicular from the point N on the principal axis.
Considering small angles,
tan<NOM = (MN)/(OM)
tan < NCM = (MN/MC)
tan<NIM = (MN)/(MI)
Now, for ΔNOC, <i is the exterior angle. Therefore, i = ∠NOM + ∠NCM
i = (MN/OM)+(MN/MC) (equation (1))
Similarly, r = ∠NCM – ∠NIM
e., r = (MN/MC) – (MN/MI) (equation (2))
Now, by Snell’s law n1 sin i = n2 sin r or for small angles
n1i = n2r
Substituting i and r from Equation. (1) and (2), we get
(n1/OM) + (n2/MI) = (n2 – n1)/MC) Equation (3)
Here, OM, MI and MC represent magnitudes of distances. Applying the Cartesian sign convention,
OM = –u, MI = +v, MC = +R
Substituting these in Eq. (3), we get,
(n2 –v) –(n1/u) = (n2 – n1)/(R) Equation (4)
Equation (4) gives us a relation between object and image distance in terms of refractive index of the medium and the radius of curvature of the curved spherical surface. It holds for any curved spherical surface.
Refraction by Lens: Convex & Concave
A ray of light incident on the lens parallel to the principal axis after refraction passes through second principal axis.
A ray of light passing through first principal focus after refraction should move parallel to the principal axis.
A ray of light passing through the optical centre should go-undeviated after refraction.
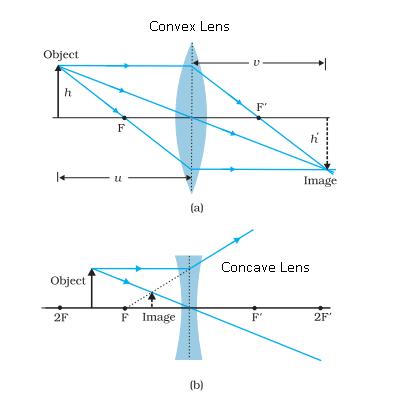
1. Magnification of a lens
It is the ratio of the size of the image to the size of the object.
It is denoted as m =(h’/h) = (v/u)
For a virtual and erect image is formed by a convex lens or by concave lens, m is positive and for real and inverted image m is negative.
Combination of thin lenses in contact
Let us consider two lenses A and B of focal length f1 and f2 placed in contact with each other. An object is placed at O beyond the focus of the first lens A on the common principal axis.
The lens A produces an image at I1 . This image I1 acts as the object for the second lens B. The final image is produced at I as shown in Fig. Since the lenses are thin, a common optical centre P is chosen.
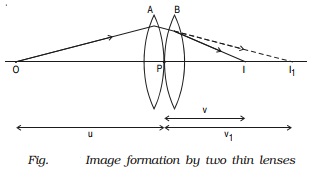
Let PO = u, object distance for the first lens (A), PI = v, final image distance and PI1 = v1, image distance for the first lens (A) and also object distance for second lens (B).
For the image I1 produced by the first lens A,
1/v1 ? 1/u = 1/f1 ????..(1)
For the final image I, produced by the second lens B,
1/v - 1/v1 = 1/f2 ????..(2)
Adding equations (1) and (2),
1/v ? 1/u = 1/f1 + 1/f2 ????..(3)
If the combination is replaced by a single lens of focal length F such that it forms the image of O at the same position I, then
1/v - 1/u = 1/F ????(4)
From equations (3) and (4)
1/F = 1/f1 + 1/f2 ?????(5)
This F is the focal length of the equivalent lens for the combination. The derivation can be extended for several thin lenses of focal
lengths f1, f2, f3 ... in contact. The effective focal length of the combination is given by
1/F = 1/f1 + 1/f2 + 1/f3 + ?????.. ?..(6)
In terms of power, equation (6) can be written as
P = P1 + P2 + P3 + .... ...(7)
Equation (7) may be stated as follows :
The power of a combination of lenses in contact is the algebraic sum of the powers of individual lenses.
2. Prism
- Books Name
- Physics Book Part l and ll
- Publication
- Grow Career Publication
- Course
- CBSE Class 12
- Subject
- Physics
Prism
A prism is a transparent medium bounded by the three plane faces. Out of the three faces, one is grounded and the other two are polished. The polished faces are called refracting faces. The angle between the refracting faces is called angle of prism, or the refracting angle. The third face is called base of the prism.
Refraction of light through a prism
Fig. shows the cross section of a triangular prism ABC, placed in air. Let ?A? be the refracting angle of the prism. A ray of light PQ incident on the refracting face AB, gets refracted along QR and emerges along RS. The angle of incidence and refraction at the two faces are i1, r1 , r2 and i2 respectively. The angle between the incident ray PQ and the emergent ray RS is called angle of deviation, d. In the ∆QER, the exterior angle FER = angle EQR + angle ERQ
d = (i1 - r1) + (i2 - r2)
d = (i1 + i2) - (r1 + r2) ????.(1)
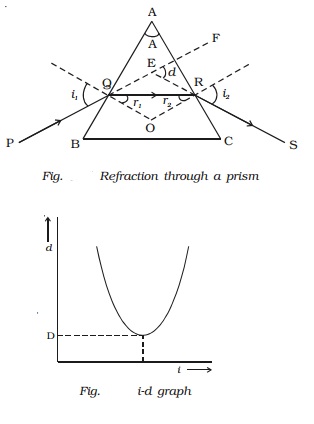
In the quadrilateral AQOR, the angles at Q and R are right angles
Angle Q + Angle R = 1800
A + Angle R = 1800 ????.(2)
Also, from the ∆QOR
r1+ r2 = A ??????..(4)
Substituting in (1),
d = i1 + i2 - A
or A + d = i1 + i2 ...(5)
For a given prism and for a light of given wavelength, the angle of deviation depends upon the angle of incidence.
As the angle of incidence i gradually increases, the angle of deviation d decreases, reaches a minimum value D and then
increases. D is called the angle of minimum deviation. It will be seen from the graph (Fig. ) that there is only one angle of
incidence for which the deviation is a minimum.
At minimum deviation position the incident ray and emergent ray are symmetric with respect to the base of the prism. (i.e)the refracted ray QR is parallel to the base of the prism.
At the minimum deviation
i1 = i2 = i and r1 = r2 = r
from equation (4) 2r = A or r = A/2
and from equation (5) 2i = A + D or i = ( A+D )/2
The refractive index is ? = sin i/sin r
? = [sin((A+D) / 2)] / sin(A/2)
- Dispersion of light
Dispersion is the splitting of white light into its constituent colours. This band of colours of light is called its spectrum.
In the visible region of spectrum, the spectral lines are seen in the order from violet to red. The colours are given by the word VIBGYOR (Violet,Indigo, Blue, Green,Yellow, Orange and Red) (Fig. )
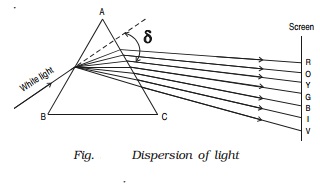
The origin of colour after passing through a prism was a matter of much debate in physics. Does the prism itself create colour in some
way or does it only separate the colours already present in white light?
Optical Instruments
- Optical instruments are instruments using reflecting and refracting properties of mirrors, lenses and prisms.
- A number of optical devices and instruments have been designed utilising reflecting and refracting properties of mirrors, lenses and prisms.
- Periscope, kaleidoscope, binoculars, telescopes; microscopes are some examples of optical devices and instruments.
- Some of optical instruments which consists of lenses and prisms are:-
1.Binoculars
2.Telescope
3.Microscope
4.Eye

 Grow Career Publication
Grow Career Publication
