- Books Name
- Mathmatics Book Based on NCERT
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 12
- Subject
- Mathmatics
Partitions,total probability, Bayes’ theorem
Partition of a sample space
A set of events E1, E2, ..., En is said to represent a partition of the sample space S if
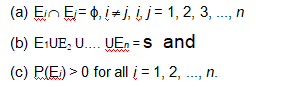
Theorem of total probability
Let {E1, E2,...,En} be a partition of the sample space S, and suppose that each of the events E1, E2,..., En has nonzero probability of occurrence. Let A be any event associated with S, then
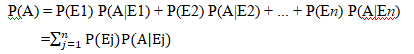
Proof: Given that E1, E2,..., En is a partition of the sample space S . Therefore,
S = E1 U E2 U ... U En and Ei Ç Ej = ɸ, i ¹ j, i, j = 1, 2, 3, ..., n
Now, we know that for any event A,
A = A ÇS
= A Ç (E1 U E2 U ... U En)
= (A Ç E1) U (AÇ E2) U ... U (AÇ En)
Also A ÇEi and A ÇEj are respectively the subsets of Ei and Ej .
We know that
Ei and Ej are disjoint, for i ¹ j , therefore, A Ç Ei and A Ç Ej are also disjoint for all
i ¹j, i, j = 1, 2, ..., n.
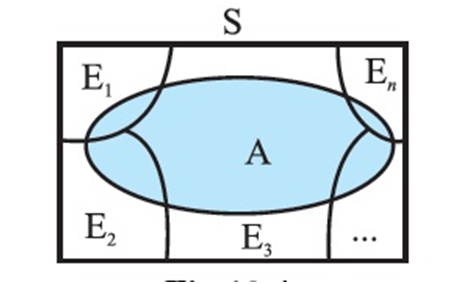
Thus, P(A) = P [(A Ç E1) U (AÇ E2) U ... U (AÇ En)]
= P (A Ç E1) + P (A Ç E2) + ... + P (A Ç En)
Now, by multiplication rule of probability,
we have
P(A Ç Ei) = SP(Ei) P(A|Ei) as P (Ei) > 0 "i = 1,2,..., n
Therefore, P (A) = P (E1) P (A|E1) + P (E2) P (A|E2) + ... + P (En)P(A|En)
![]()
Example : A person has undertaken a construction job. The probabilities are 0.65 that there will be strike, 0.80 that the construction job will be completed on time if there is no strike, and 0.32 that the construction job will be completed on time if there is a strike. Determine the probability that the construction job will be completed on time.
Solution : Let A be the event that the construction job will be completed on time, and B
be the event that there will be a strike. We have to find P(A).
We have
P(B) = 0.65, P(no strike) = P(B¢) = 1 - P(B) = 1 - 0.65 = 0.35
P(A|B) = 0.32, P(A|B¢) = 0.80
Since events B and B_ form a partition of the sample space S, therefore, by theorem
on total probability, we have
P(A) = P(B) P(A|B) + P(B¢) P(A|B¢)
= 0.65 × 0.32 + 0.35 × 0.8
= 0.208 + 0.28 = 0.488
Thus, the probability that the construction job will be completed in time is 0.488.
Bayes’ Theorem:
If E1, E2 ,..., En are n non empty events which constitute a partition of sample space S, i.e. E1, E2 ,..., En are pairwise disjoint and E1UE2U ... UEn = S and A is any event of nonzero probability, then
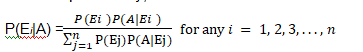
Proof: By formula of conditional probability, we know that

Hence Proved.
N.B.: -
- The events E1, E2, ..., En are called hypotheses.
- The probability P(Ei) is called the priori probability of the hypothesis Ei
- The conditional probability P(Ei |A) is called a posteriori probability of the
hypothesis Ei.
Example : Given three identical boxes I, II and III, each containing two coins. In
box I, both coins are gold coins, in box II, both are silver coins and in the box III, there
is one gold and one silver coin. A person chooses a box at random and takes out a coin.
If the coin is of gold, what is the probability that the other coin in the box is also of gold?
Solution Let E1, E2 and E3 be the events that boxes I, II and III are chosen, respectively.
Then P(E1) = P(E2) = P(E3) =![]()
Let A be the event that ‘the coin drawn is of gold’
Then P(A|E1) = P(a gold coin from bag I) = ![]()
P(A|E2) = P(a gold coin from bag II) = ![]() 0
0
P(A|E3) = P(a gold coin from bag III) =![]()
Now, the probability that the other coin in the box is of gold
= the probability that gold coin is drawn from the box I.
= P(E1|A)
By Bayes' theorem, we know that
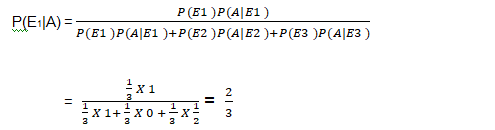
Example : A man is known to speak truth 3 out of 4 times. He throws a die and reports that it is a six. Find the probability that it is actually a six.
Solution: Let E be the event that the man reports that six occurs in the throwing of the die and let S1 be the event that six occurs and S2 be the event that six does not occur.
Then P(S1) = Probability that six occurs = ![]()
P(S2) = Probability that six does not occur = ![]()
P(E|S1) = Probability that the man reports that six occurs when six has
actually occurred on the die
= Probability that the man speaks the truth = ![]()
P(E|S2) = Probability that the man reports that six occurs when six has
not actually occurred on the die
= Probability that the man does not speak the truth = 1-![]() =
= ![]()
Thus, by Bayes' theorem, we get
P(S1|E) = Probability that the report of the man that six has occurred is
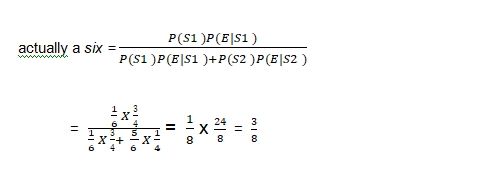

 KRISHNA PUBLICATIONS
KRISHNA PUBLICATIONS
