PHP (Hypertext Preprocessor)
PHP is an open-source, interpreted, and object-oriented scripting language that can be executed at the server-side. PHP is well suited for web development. Therefore, it is used to develop web applications (an application that executes on the server and generates the dynamic page.).
More About PHP
PHP was developed by Rasmus Lerdorf in 1995 and is later being developed as an open-source. PHP group now manages the implementation of PHP.
PHP has many syntaxes similar to C, Java, and Perl, and has many unique features and specific functions.
PHP page is a file with a .php extension can contain a combination of HTML Tags and PHP scripts.
PHP recursive acronym for PHP (Hypertext Preprocessor): HyperText means, text containing all sorts of web markups, PreProcessor means all of the HyperText is processed first and then the result is sent as pure HTML to the web browser. A client cannot see the PHP source code because it is preprocessed and interpreted.
PHP is Server-side scripting language: Server-side scripting means that the PHP code is processed on the web server rather than the client machine.
PHP supports many databases (MySQL and PHP combination is widely used).
PHP is an open-source scripting language.
PHP is free to download and use.
Popular Online Web Applications Developed in PHP / Frameworks of PHP.
|
CMS Made in PHP |
FrameWorks in PHP |
WordPress |
Laravel |
Joomla |
CodeIgniter |
Drupal |
Symfony |
SilverStripe |
CakePHP |
PHP Fusion |
Yii |
PHP Features
Execution of PHP
To run PHP code, you need the following three software on your local machine:
- Web Server (e.g., Apache)
- PHP (Interpreter)
- MySQL Databases (optional)
I will suggest you to install AMP (Apache, MySQL, PHP) software stack. It is available for all operating systems. There are many AMP options available in the market that are given below:
- WAMP for Windows
- LAMP for Linux
- MAMP for Mac
- XAMPP (Cross, Apache, MySQL, PHP, Perl) for Cross Platform: It includes some other components too such as FileZilla, OpenSSL, Webalizer, Mercury Mail, etc.
How PHP Works
There are 80% websites are developed using php, some of the best websites are:
|
|
|
|
Wikipedia |
|
|
Tumblr |
|
|
Yahoo |
|
|
Flickr |
|
|
Friendster |
|
|
Istockphoto |
|
|
sourceforge.net |
- Books Name
- Max Foundation Mathmatics Book
- Publication
- Max Publication
- Course
- CBSE Class 12
- Subject
- Mathmatics
Chapter no. 1 : Electric charges and Field
Topic no. 1.1 Basics of electric charges
Lecture no. 1/3
Lecture Topic: Basics of Electric Charges
Electrostatics : Electro = Charge + Statics = Rest
Electrostatics – The branch of physics tht deals with study of electrostatic force, electric field and electric potential due to stationary charge.
Chapter 01. Electric charges and Field
1.1. Electric charges
1.2. Coulomb’s law in electrostatics
1.3. Electric field and electric dipole
1.4. Electric field lines and gauss’s theorem
Chapter 0 2. Electric Potential and Capacitance
2.1 Electric potential
2.2 Capacitance
- Books Name
- SonikaAnandAcademy Mathmatics Book
- Publication
- SonikaAnandAcademy
- Course
- CBSE Class 12
- Subject
- Mathmatics
How we will distinguish between one one and many one function
It is also explained as what is the other name of one one function that is one one function is also named as injective function whereas many one function is also known as surjective function
A function as both one one and onto then it is also known as bijective function
- Books Name
- ABCD CLASSES Mathmatics Book
- Publication
- ABCD CLASSES
- Course
- CBSE Class 12
- Subject
- Mathmatics
Types of Relations
Given below is a list of different types of relations:
- Empty Relation
- Universal Relation
- Identity Relation
- Inverse Relation
- Reflexive Relation
- Symmetric Relation
- Transitive Relation
- Equivalence Relation
1) Empty Relation - A relation is an empty relation if it has no elements, that is, no element of set A is mapped or linked to any element of A. It is denoted by R = ∅.
For example, if set A = {1, 2, 3} then, one of the void relations can be R = {x, y} where, |x – y| = 8. For empty relation,
R = φ ⊂ A × A
2) Universal Relation - A relation R in a set A is a universal relation if each element of A is related to every element of A, i.e., R = A × A. It is called the full relation.
Consider set A = {a, b, c}. Now one of the universal relations will be R = {x, y} where, |x – y| ≥ 0. For universal relation,
R = A × A
3) Identity Relation - A relation R on A is said to be an identity relation if each element of A is related to itself, that is, R = {(a, a) : for all a ∈ A}
For example, in a set A = {a, b, c}, the identity relation will be I = {a, a}, {b, b}, {c, c}. For identity relation,
I = {(a, a), a ∈ A}
4) Inverse Relation - Define R to be a relation from set P to set Q i.e., R ∈ P × Q. The relation R-1 is said to be an Inverse relation if R-1 from set Q to P is denoted by R-1 = {(q, p): (p, q) ∈ R}.
For example if set A = {(a, b), (c, d)}, then inverse relation will be R-1 = {(b, a), (d, c)}. So, for an inverse relation,
R-1 = {(b, a): (a, b) ∈ R}
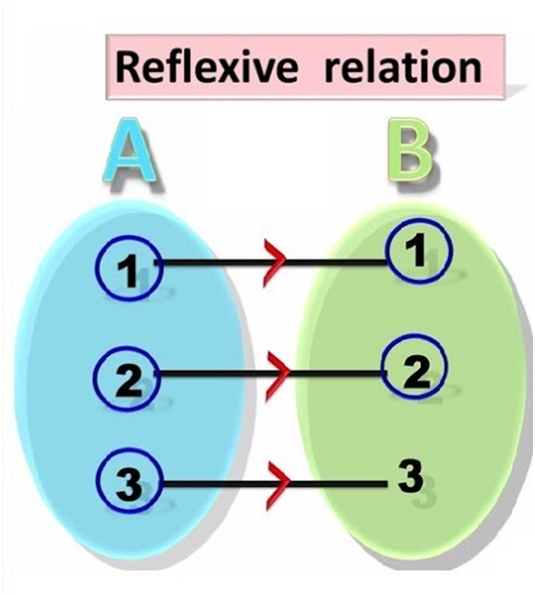
5) Reflexive Relation - A binary relation R defined on a set A is said to be reflexive if, for every element a ∈ A, we have aRa, that is, (a, a) ∈ R.
For example, consider a set A = {1, 2,}. Now an example of reflexive relation will be R = {(1, 1), (2, 2), (1, 2), (2, 1)}. The reflexive relation is given by-
(a, a) ∈ R

6) Symmetric Relation - A binary relation R defined on a set A is said to be symmetric if and only if, for elements a, b ∈ A, we have aRb, that is, (a, b) ∈ R, then we must have bRa, that is, (b, a) ∈ R.
An example of symmetric relation will be R = {(1, 2), (2, 1)} for a set A = {1, 2}. So, for a symmetric relation,
aRb ⇒ bRa, ∀ a, b ∈ A
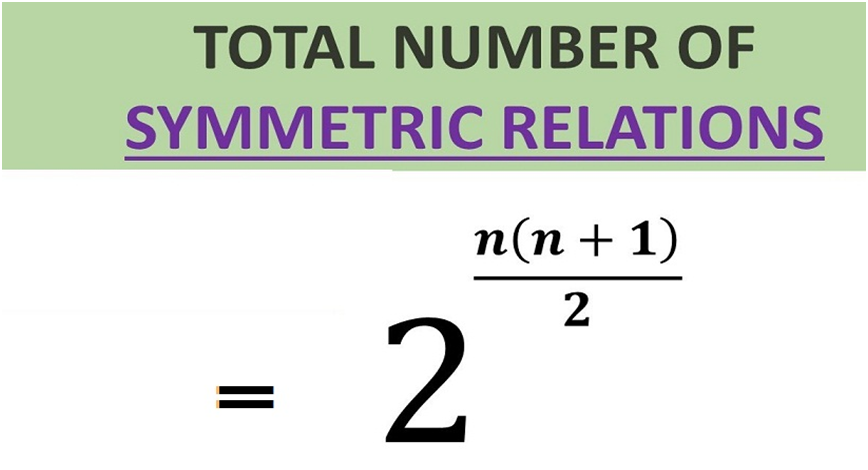
Example: For the set P={a,b}, the relation R={(a,b),(b,a)} is called symmetric relation, where a,b∈P.
7) Transitive Relation - A relation R is transitive if and only if (a, b) ∈ R and (b, c) ∈ R ⇒ (a, c) ∈ R for a, b, c ∈ A
Example: For the set A ={a,b,c}, the relation R={(a,b),(b,c),(a,c)} is called transitive relation, where a,b,c∈ A.
8) Equivalence Relation - A relation R defined on a set A is said to be an equivalence relation if and only if it is reflexive, symmetric and transitive.
Conditions:
1. If the relation (R) is reflexive, then all the elements of set A are mapped with itself, such that for every x∈ A , then (x,x)∈R.
2. The relation (R) is symmetric on set A, if (x,y)∈R, then (y,x)∈R, such that a,b∈ A.
3. The relation R on set A, if (x,y)∈R and (y,z)∈R, then (x,z)∈R, for all a,b,c∈ A is called transitive relation.
Example: Let A = {1, 2, 3, 4} and R = {(1, 1), (1, 3), (2, 2), (2, 4), (3, 1), (3, 3), (4, 2), (4, 4)}.
Show that R is an Equivalence Relation.
Solution:
Reflexive: Relation R is reflexive as (1, 1), (2, 2), (3, 3) and (4, 4) ∈ R.
Symmetric: Relation R is symmetric because whenever (a, b) ∈ R, (b, a) also belongs to R.
Example: (2, 4) ∈ R ⟹ (4, 2) ∈ R.
Transitive: Relation R is transitive because whenever (a, b) and (b, c) belongs to R, (a, c) also belongs to R.
Example: (3, 1) ∈ R and (1, 3) ∈ R ⟹ (3, 3) ∈ R.
So, as R is reflexive, symmetric and transitive, hence, R is an Equivalence Relation.
Question 1:
Let us assume that F is a relation on the set R real numbers defined by x F y if and only if x-y is an integer. Prove that F is an equivalence relation on R.
Solution:
Reflexive: Let x belongs to R,then x – x = 0 which is an integer.
Therefore x F x.
So , F is reflexive.
Symmetric: Let x and y belongs to R and x F y.
- x – y is an integer.
- Thus, y – x = – ( x – y), y – x is also an integer.
- Therefore yFx.
So , F is Symmetric.
Transitive: Let x and y belongs to R, xFy and yFz.
- x-y and y-z are integers.
- ( x – y ) + ( y – z ) = x – z is also an integer.
- So that xFz.
So , F is Transitive.
Thus, R is an equivalence relation on R.
Question 2:
Show that the relation R is an equivalence relation in the set A = { 1, 2, 3, 4, 5 } given by the relation R = { (a, b):|a-b| is even }.
Solution:
R = { (a, b):|a-b| is even }. Where a, b belongs to A
Reflexive Property :
Let a is belongs to A.
|a – a| = | 0 |=0
- 0 is always even.
- Thus, |a-a| is even
- Therefore, (a, a) belongs to R
Hence R is Reflexive
Symmetric Property :
Let a, b belongs to A
|a – b| = |b – a|
Let a R b
We know that |a – b| = |-(b – a)|= |b – a|
- |a – b| is even,
- |b – a| is also even.
Therefore, if (a, b) ∈ R, then (b, a) belongs to R
Hence R is symmetric.
Transitive Property :
Let a, b, c belongs to A
Let a R b and b R c
- |b-c| is even and (b-c) is even
Since , If |a-b| is even, then (a-b) is even.
Sum of even number is also even
- a-b+ b-c is even
- a – c is also even
Then, a R c
So,
|a – b| and |b – c| is even , then |a-c| is even.
Therefore, if (a, b) ∈ R and (b, c) ∈ R, then (a, c) also belongs to R
Hence R is transitive.
Therefore R is an equivalence relation.
Equivalence Class
Let R be an equivalence relation on set A. For each a∈A, we denote the equivalence class of a as [a] defined as:
[a]={x ∈A ∣ x R a}
Example:
Define a relation ∼ on Z by
a∼b⇔a mod 4=b mod 4
Find the equivalence classes of ∼
Answer
Two integers will be related by ∼ if they have the same remainder after dividing
by 4. The possible remainders are 0, 1, 2, 3
[0]={...,−12,−8,−4,0,4,8,12,...}
[1]={...,−11,−7,−3,1,5,9,13,...}
[2]={...,−10,−6,−2,2,6,10,14,...}
[3]={...,−9,−5,−1,3,7,11,15,...}
Example:
Let S=P({1,2,3})={∅,{1},{2},{3},{1,2},{1,3},{2,3},{1,2,3}}.
For convenience, label
S0=∅,S1={1},S2={2},S3={3},S4={1,2},S5={1,3},S6={2,3},S7={1,2,3}.
Define this equivalence relation ∼ on S by
Si∼Sj⇔|Si|=|Sj|
Find the equivalence classes of ∼.
Answer
Two sets will be related by ∼ if they have the same number of elements.
[S0]={S0}
[S2]={S1,S2,S3}
[S4]={S4,S5,S6}
[S7]={S7}
Example:
Consider set S={a,b,c,d} with this partition: {{a,b},{c},{d}}.
Find the ordered pairs for the relation R, induced by the partition.
Proof
R={(a,a),(a,b),(b,a),(b,b),(c,c),(d,d)}
Question :
Let R be a relation from N to N defined by R = {(a, b): a, b ∈ N and a = b2}. Are the following true?
(i) (a, a) ∈ R, for all a ∈ N
(ii) (a, b) ∈ R, implies (b, a) ∈ R
(iii) (a, b) ∈ R, (b, c) ∈ R implies (a, c) ∈ R.
Justify your answer in each case.
ANSWER:
R = {(a, b): a, b ∈ N and a = b2}
(i) It can be seen that 2 ∈ N;however, 2 ≠ 22 = 4.
Therefore, the statement “(a, a) ∈ R, for all a ∈ N” is not true.
(ii) It can be seen that (9, 3) ∈ N because 9, 3 ∈ N and 9 = 32.
Now, 3 ≠ 92 = 81; therefore, (3, 9) ∉ N
Therefore, the statement “(a, b) ∈ R, implies (b, a) ∈ R” is not true.
(iii) It can be seen that (16, 4) ∈ R, (4, 2) ∈ R because 16, 4, 2 ∈ N and 16 = 42 and 4 = 22.
Now, 16 ≠ 22 = 4; therefore, (16, 2) ∉ N
Therefore, the statement “(a, b) ∈ R, (b, c) ∈ R implies (a, c) ∈ R” is not true.
Example 5: Check whether the relation R defined in the set {1, 2, 3, 4, 5, 6} as R = {(a, b): b = a + 1} is reflexive, symmetric or transitive.
Solution:
Given R = {(a, b): b = a + 1}
Now for this relation we have to check whether it is reflexive, transitive and symmetric Reflexivity:
Let a be an arbitrary element of R.
Then, a = a + 1 cannot be true for all a ∈ A.
⇒ (a, a) ∉ R
So, R is not reflexive on A.
Symmetry:
Let (a, b) ∈ R
⇒ b = a + 1
⇒ −a = −b + 1
⇒ a = b − 1
Thus, (b, a) ∉ R
So, R is not symmetric on A.
Transitivity:
Let (1, 2) and (2, 3) ∈ R
⇒ 2 = 1 + 1 and 3
2 + 1 is true.
But 3 ≠ 1+1
⇒ (1, 3) ∉ R
So, R is not transitive on A.
Example 6: Check whether the relation R on R defined as R = {(a, b): a ≤ b3} is reflexive, symmetric or transitive.
Solution:
Given R = {(a, b): a ≤ b3}
It is observed that (1/2, 1/2) in R as 1/2 > (1/2)3 = 1/8
∴ R is not reflexive.
Now,
(1, 2) ∈ R (as 1 < 23 = 8)
But,
(2, 1) ∉ R (as 2 > 13 = 1)
∴ R is not symmetric.
We have (3, 3/2), (3/2, 6/5) in “R as” 3 < (3/2)3 and 3/2 < (6/5)3
But (3, 6/5) ∉ R as 3 > (6/5)3
∴ R is not transitive.
Hence, R is neither reflexive, nor symmetric, nor transitive.
Example 7: Prove that every identity relation on a set is reflexive, but the converse is not necessarily true.
Solution:
Let A be a set.
Then, Identity relation IA=IA is reflexive, since (a, a) ∈ A ∀a
The converse of it need not be necessarily true.
Consider the set A = {1, 2, 3}
Here,
Relation R = {(1, 1), (2, 2) , (3, 3), (2, 1), (1, 3)} is reflexive on A.
However, R is not an identity relation.
Example 8: If A = {1, 2, 3, 4} define relations on A which have properties of being
(i) Reflexive, transitive but not symmetric
(ii) Symmetric but neither reflexive nor transitive.
(iii) Reflexive, symmetric and transitive.
Solution:
(i) The relation on A having properties of being reflexive, transitive, but not symmetric is
R = {(1, 1), (2, 2), (3, 3), (4, 4), (2, 1)}
Relation R satisfies reflexivity and transitivity.
⇒ (1, 1), (2, 2), (3, 3) ∈ R
And (1, 1), (2, 1) ∈ R ⇒ (1, 1) ∈ R
However, (2, 1) ∈ R, but (1, 2) ∉ R
(ii) The relation on A having properties of being reflexive, transitive, but not symmetric is
R = {(1, 1), (2, 2), (3, 3), (4, 4), (2, 1)}
Relation R satisfies reflexivity and transitivity.
⇒ (1, 1), (2, 2), (3, 3) ∈ R
And (1, 1), (2, 1) ∈ R ⇒ (1, 1) ∈ R
However, (2, 1) ∈ R, but (1, 2) ∉ R
(iii) The relation on A having properties of being symmetric, reflexive and transitive is
R = {(1, 1), (2, 2), (3, 3), (4, 4), (1, 2), (2, 1)}
The relation R is an equivalence relation on A.
Example 9:. Show that the relation R defined by R = {(a, b): a – b is divisible by 3; a, b ∈ Z} is an equivalence relation.
Solution:
Given R = {(a, b): a – b is divisible by 3; a, b ∈ Z} is a relation
To prove equivalence relation it is necessary that the given relation should be reflexive, symmetric and transitive.
Let us check these properties on R.
Reflexivity:
Let a be an arbitrary element of R.
Then, a – a = 0 = 0 × 3
⇒ a − a is divisible by 3
⇒ (a, a) ∈ R for all a ∈ Z
So, R is reflexive on Z.
Symmetry:
Let (a, b) ∈ R
⇒ a − b is divisible by 3
⇒ a − b = 3p for some p ∈ Z
⇒ b − a = 3 (−p)
Here, −p ∈ Z
⇒ b − a is divisible by 3
⇒ (b, a) ∈ R for all a, b ∈ Z
So, R is symmetric on Z.
Transitivity:
Let (a, b) and (b, c) ∈ R
⇒ a − b and b − c are divisible by 3
⇒ a – b = 3p for some p ∈ Z
And b − c = 3q for some q ∈ Z
Adding the above two equations, we get
a − b + b – c = 3p + 3q
⇒ a − c = 3 (p + q)
Here, p + q ∈ Z
⇒ a − c is divisible by 3
⇒ (a, c) ∈ R for all a, c ∈ Z
So, R is transitive on Z.
Therefore R is reflexive, symmetric and transitive.
Hence, R is an equivalence relation on Z.
Example 10: Show that the relation R on the set Z of integers, given by
R = {(a, b): 2 divides a – b}, is an equivalence relation.
Solution:
Given R = {(a, b): 2 divides a – b} is a relation defined on Z.
To prove equivalence relation it is necessary that the given relation should be reflexive, symmetric and transitive.
Let us check these properties on R.
Reflexivity:
Let a be an arbitrary element of the set Z.
Then, a ∈ R
⇒ a − a = 0 = 0 × 2
⇒ 2 divides a − a
⇒ (a, a) ∈ R for all a ∈ Z
So, R is reflexive on Z.
Symmetry:
Let (a, b) ∈ R
⇒ 2 divides a − b
⇒ (a-b)/2 = p for some p ∈ Z
⇒ (b-a)/2 = – p
Here, −p ∈ Z
⇒ 2 divides b − a
⇒ (b, a) ∈ R for all a, b ∈ Z
So, R is symmetric on Z
Transitivity:
Let (a, b) and (b, c) ∈ R
⇒ 2 divides a−b and 2 divides b−c
⇒ (a-b)/2 = p and (b-c)/2 = q for some p, q ∈ Z
Adding the above two equations, we get
(a – b)/2 + (b – c)/2 = p + q
⇒ (a – c)/2 = p +q
Here, p+ q ∈ Z
⇒ 2 divides a − c
⇒ (a, c) ∈ R for all a, c ∈ Z
So, R is transitive on Z.
Therefore R is reflexive, symmetric and transitive.
Hence, R is an equivalence relation on Z.
Example 11:. Prove that the relation R on Z defined by (a, b) ∈ R ⇔ a − b is divisible by 5 is an equivalence relation on Z.
Solution:
Given relation R on Z defined by (a, b) ∈ R ⇔ a − b is divisible by 5
To prove equivalence relation it is necessary that the given relation should be reflexive, symmetric and transitive.
Let us check these properties on R.
Reflexivity:
Let a be an arbitrary element of R. Then,
⇒ a − a = 0 = 0 × 5
⇒ a − a is divisible by 5
⇒ (a, a) ∈ R for all a ∈ Z
So, R is reflexive on Z.
Symmetry:
Let (a, b) ∈ R
⇒ a − b is divisible by 5
⇒ a − b = 5p for some p ∈ Z
⇒ b − a = 5 (−p)
Here, −p ∈ Z [Since p ∈ Z]
⇒ b − a is divisible by 5
⇒ (b, a) ∈ R for all a, b ∈ Z
So, R is symmetric on Z.
Transitivity:
Let (a, b) and (b, c) ∈ R
⇒ a − b is divisible by 5
⇒ a − b = 5p for some Z
Also, b − c is divisible by 5
⇒ b − c = 5q for some Z
Adding the above two equations, we get
a −b + b − c = 5p + 5q
⇒ a − c = 5 ( p + q )
⇒ a − c is divisible by 5
Here, p + q ∈ Z
⇒ (a, c) ∈ R for all a, c ∈ Z
So, R is transitive on Z.
Therefore R is reflexive, symmetric and transitive.
Hence, R is an equivalence relation on Z.
Example 12:. Let n be a fixed positive integer. Define a relation R on Z as follows:
(a, b) ∈ R ⇔ a − b is divisible by n.
Show that R is an equivalence relation on Z.
Solution:
Given (a, b) ∈ R ⇔ a − b is divisible by n is a relation R defined on Z.
To prove equivalence relation it is necessary that the given relation should be reflexive, symmetric and transitive.
Let us check these properties on R.
Reflexivity:
Let a ∈ N
Here, a − a = 0 = 0 × n
⇒ a − a is divisible by n
⇒ (a, a) ∈ R
⇒ (a, a) ∈ R for all a ∈ Z
So, R is reflexive on Z.
Symmetry:
Let (a, b) ∈ R
Here, a − b is divisible by n
⇒ a − b = n p for some p ∈ Z
⇒ b − a = n (−p)
⇒ b − a is divisible by n [ p ∈ Z⇒ − p ∈ Z]
⇒ (b, a) ∈ R
So, R is symmetric on Z.
Transitivity:
Let (a, b) and (b, c) ∈ R
Here, a − b is divisible by n and b − c is divisible by n.
⇒ a − b= n p for some p ∈ Z
And b−c = n q for some q ∈ Z
a – b + b − c = n p + n q
⇒ a − c = n (p + q)
⇒ (a, c) ∈ R for all a, c ∈ Z
So, R is transitive on Z.
Therefore R is reflexive, symmetric and transitive.
Hence, R is an equivalence relation on Z
- Books Name
- Mathmatics Book Based on NCERT
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 12
- Subject
- Mathmatics
Types of Relations
Given below is a list of different types of relations:
- Empty Relation
- Universal Relation
- Identity Relation
- Inverse Relation
- Reflexive Relation
- Symmetric Relation
- Transitive Relation
- Equivalence Relation
1) Empty Relation - A relation is an empty relation if it has no elements, that is, no element of set A is mapped or linked to any element of A. It is denoted by R = ∅.
For example, if set A = {1, 2, 3} then, one of the void relations can be R = {x, y} where, |x – y| = 8. For empty relation,
R = φ ⊂ A × A
2) Universal Relation - A relation R in a set A is a universal relation if each element of A is related to every element of A, i.e., R = A × A. It is called the full relation.
Consider set A = {a, b, c}. Now one of the universal relations will be R = {x, y} where, |x – y| ≥ 0. For universal relation,
R = A × A
3) Identity Relation - A relation R on A is said to be an identity relation if each element of A is related to itself, that is, R = {(a, a) : for all a ∈ A}
For example, in a set A = {a, b, c}, the identity relation will be I = {a, a}, {b, b}, {c, c}. For identity relation,
I = {(a, a), a ∈ A}
4) Inverse Relation - Define R to be a relation from set P to set Q i.e., R ∈ P × Q. The relation R-1 is said to be an Inverse relation if R-1 from set Q to P is denoted by R-1 = {(q, p): (p, q) ∈ R}.
For example if set A = {(a, b), (c, d)}, then inverse relation will be R-1 = {(b, a), (d, c)}. So, for an inverse relation,
R-1 = {(b, a): (a, b) ∈ R}
5) Reflexive Relation - A binary relation R defined on a set A is said to be reflexive if, for every element a ∈ A, we have aRa, that is, (a, a) ∈ R.
For example, consider a set A = {1, 2,}. Now an example of reflexive relation will be R = {(1, 1), (2, 2), (1, 2), (2, 1)}. The reflexive relation is given by-
(a, a) ∈ R


6) Symmetric Relation - A binary relation R defined on a set A is said to be symmetric if and only if, for elements a, b ∈ A, we have aRb, that is, (a, b) ∈ R, then we must have bRa, that is, (b, a) ∈ R.
An example of symmetric relation will be R = {(1, 2), (2, 1)} for a set A = {1, 2}. So, for a symmetric relation,
aRb ⇒ bRa, ∀ a, b ∈ A
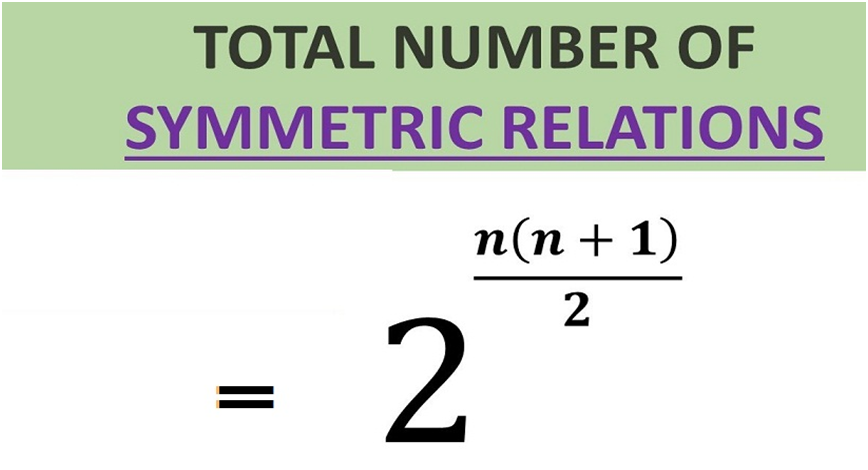
Example: For the set P={a,b}, the relation R={(a,b),(b,a)} is called symmetric relation, where a,b∈P.
7) Transitive Relation - A relation R is transitive if and only if (a, b) ∈ R and (b, c) ∈ R ⇒ (a, c) ∈ R for a, b, c ∈ A
Example: For the set A ={a,b,c}, the relation R={(a,b),(b,c),(a,c)} is called transitive relation, where a,b,c∈ A.
8) Equivalence Relation - A relation R defined on a set A is said to be an equivalence relation if and only if it is reflexive, symmetric and transitive.
Conditions:
1. If the relation (R) is reflexive, then all the elements of set A are mapped with itself, such that for every x∈ A , then (x,x)∈R.
2. The relation (R) is symmetric on set A, if (x,y)∈R, then (y,x)∈R, such that a,b∈ A.
3. The relation R on set A, if (x,y)∈R and (y,z)∈R, then (x,z)∈R, for all a,b,c∈ A is called transitive relation.
Example: Let A = {1, 2, 3, 4} and R = {(1, 1), (1, 3), (2, 2), (2, 4), (3, 1), (3, 3), (4, 2), (4, 4)}.
Show that R is an Equivalence Relation.
Solution:
Reflexive: Relation R is reflexive as (1, 1), (2, 2), (3, 3) and (4, 4) ∈ R.
Symmetric: Relation R is symmetric because whenever (a, b) ∈ R, (b, a) also belongs to R.
Example: (2, 4) ∈ R ⟹ (4, 2) ∈ R.
Transitive: Relation R is transitive because whenever (a, b) and (b, c) belongs to R, (a, c) also belongs to R.
Example: (3, 1) ∈ R and (1, 3) ∈ R ⟹ (3, 3) ∈ R.
So, as R is reflexive, symmetric and transitive, hence, R is an Equivalence Relation.
Question 1:
Let us assume that F is a relation on the set R real numbers defined by x F y if and only if x-y is an integer. Prove that F is an equivalence relation on R.
Solution:
Reflexive: Let x belongs to R,then x – x = 0 which is an integer.
Therefore x F x.
So , F is reflexive.
Symmetric: Let x and y belongs to R and x F y.
- x – y is an integer.
- Thus, y – x = – ( x – y), y – x is also an integer.
- Therefore yFx.
So , F is Symmetric.
Transitive: Let x and y belongs to R, xFy and yFz.
- x-y and y-z are integers.
- ( x – y ) + ( y – z ) = x – z is also an integer.
- So that xFz.
So , F is Transitive.
Thus, R is an equivalence relation on R.
Question 2:
Show that the relation R is an equivalence relation in the set A = { 1, 2, 3, 4, 5 } given by the relation R = { (a, b):|a-b| is even }.
Solution:
R = { (a, b):|a-b| is even }. Where a, b belongs to A
Reflexive Property :
Let a is belongs to A.
|a – a| = | 0 |=0
- 0 is always even.
- Thus, |a-a| is even
- Therefore, (a, a) belongs to R
Hence R is Reflexive
Symmetric Property :
Let a, b belongs to A
|a – b| = |b – a|
Let a R b
We know that |a – b| = |-(b – a)|= |b – a|
- |a – b| is even,
- |b – a| is also even.
Therefore, if (a, b) ∈ R, then (b, a) belongs to R
Hence R is symmetric.
Transitive Property :
Let a, b, c belongs to A
Let a R b and b R c
- |b-c| is even and (b-c) is even
Since , If |a-b| is even, then (a-b) is even.
Sum of even number is also even
- a-b+ b-c is even
- a – c is also even
Then, a R c
So,
|a – b| and |b – c| is even , then |a-c| is even.
Therefore, if (a, b) ∈ R and (b, c) ∈ R, then (a, c) also belongs to R
Hence R is transitive.
Therefore R is an equivalence relation.
Equivalence Class
Let R be an equivalence relation on set A. For each a∈A, we denote the equivalence class of a as [a] defined as:
[a]={x ∈A ∣ x R a}
Example:
Define a relation ∼ on Z by
a∼b⇔a mod 4=b mod 4
Find the equivalence classes of ∼
Answer
Two integers will be related by ∼ if they have the same remainder after dividing
by 4. The possible remainders are 0, 1, 2, 3
[0]={...,−12,−8,−4,0,4,8,12,...}
[1]={...,−11,−7,−3,1,5,9,13,...}
[2]={...,−10,−6,−2,2,6,10,14,...}
[3]={...,−9,−5,−1,3,7,11,15,...}
Example:
Let S=P({1,2,3})={∅,{1},{2},{3},{1,2},{1,3},{2,3},{1,2,3}}.
For convenience, label
S0=∅,S1={1},S2={2},S3={3},S4={1,2},S5={1,3},S6={2,3},S7={1,2,3}.
Define this equivalence relation ∼ on S by
Si∼Sj⇔|Si|=|Sj|
Find the equivalence classes of ∼.
Answer
Two sets will be related by ∼ if they have the same number of elements.
[S0]={S0}
[S2]={S1,S2,S3}
[S4]={S4,S5,S6}
[S7]={S7}
Example:
Consider set S={a,b,c,d} with this partition: {{a,b},{c},{d}}.
Find the ordered pairs for the relation R, induced by the partition.
Proof
R={(a,a),(a,b),(b,a),(b,b),(c,c),(d,d)}
Question :
Let R be a relation from N to N defined by R = {(a, b): a, b ∈ N and a = b2}. Are the following true?
(i) (a, a) ∈ R, for all a ∈ N
(ii) (a, b) ∈ R, implies (b, a) ∈ R
(iii) (a, b) ∈ R, (b, c) ∈ R implies (a, c) ∈ R.
Justify your answer in each case.
ANSWER:
R = {(a, b): a, b ∈ N and a = b2}
(i) It can be seen that 2 ∈ N;however, 2 ≠ 22 = 4.
Therefore, the statement “(a, a) ∈ R, for all a ∈ N” is not true.
(ii) It can be seen that (9, 3) ∈ N because 9, 3 ∈ N and 9 = 32.
Now, 3 ≠ 92 = 81; therefore, (3, 9) ∉ N
Therefore, the statement “(a, b) ∈ R, implies (b, a) ∈ R” is not true.
(iii) It can be seen that (16, 4) ∈ R, (4, 2) ∈ R because 16, 4, 2 ∈ N and 16 = 42 and 4 = 22.
Now, 16 ≠ 22 = 4; therefore, (16, 2) ∉ N
Therefore, the statement “(a, b) ∈ R, (b, c) ∈ R implies (a, c) ∈ R” is not true.
Example 5: Check whether the relation R defined in the set {1, 2, 3, 4, 5, 6} as R = {(a, b): b = a + 1} is reflexive, symmetric or transitive.
Solution:
Given R = {(a, b): b = a + 1}
Now for this relation we have to check whether it is reflexive, transitive and symmetric Reflexivity:
Let a be an arbitrary element of R.
Then, a = a + 1 cannot be true for all a ∈ A.
⇒ (a, a) ∉ R
So, R is not reflexive on A.
Symmetry:
Let (a, b) ∈ R
⇒ b = a + 1
⇒ −a = −b + 1
⇒ a = b − 1
Thus, (b, a) ∉ R
So, R is not symmetric on A.
Transitivity:
Let (1, 2) and (2, 3) ∈ R
⇒ 2 = 1 + 1 and 3
2 + 1 is true.
But 3 ≠ 1+1
⇒ (1, 3) ∉ R
So, R is not transitive on A.
Example 6: Check whether the relation R on R defined as R = {(a, b): a ≤ b3} is reflexive, symmetric or transitive.
Solution:
Given R = {(a, b): a ≤ b3}
It is observed that (1/2, 1/2) in R as 1/2 > (1/2)3 = 1/8
∴ R is not reflexive.
Now,
(1, 2) ∈ R (as 1 < 23 = 8)
But,
(2, 1) ∉ R (as 2 > 13 = 1)
∴ R is not symmetric.
We have (3, 3/2), (3/2, 6/5) in “R as” 3 < (3/2)3 and 3/2 < (6/5)3
But (3, 6/5) ∉ R as 3 > (6/5)3
∴ R is not transitive.
Hence, R is neither reflexive, nor symmetric, nor transitive.
Example 7: Prove that every identity relation on a set is reflexive, but the converse is not necessarily true.
Solution:
Let A be a set.
Then, Identity relation IA=IA is reflexive, since (a, a) ∈ A ∀a
The converse of it need not be necessarily true.
Consider the set A = {1, 2, 3}
Here,
Relation R = {(1, 1), (2, 2) , (3, 3), (2, 1), (1, 3)} is reflexive on A.
However, R is not an identity relation.
Example 8: If A = {1, 2, 3, 4} define relations on A which have properties of being
(i) Reflexive, transitive but not symmetric
(ii) Symmetric but neither reflexive nor transitive.
(iii) Reflexive, symmetric and transitive.
Solution:
(i) The relation on A having properties of being reflexive, transitive, but not symmetric is
R = {(1, 1), (2, 2), (3, 3), (4, 4), (2, 1)}
Relation R satisfies reflexivity and transitivity.
⇒ (1, 1), (2, 2), (3, 3) ∈ R
And (1, 1), (2, 1) ∈ R ⇒ (1, 1) ∈ R
However, (2, 1) ∈ R, but (1, 2) ∉ R
(ii) The relation on A having properties of being reflexive, transitive, but not symmetric is
R = {(1, 1), (2, 2), (3, 3), (4, 4), (2, 1)}
Relation R satisfies reflexivity and transitivity.
⇒ (1, 1), (2, 2), (3, 3) ∈ R
And (1, 1), (2, 1) ∈ R ⇒ (1, 1) ∈ R
However, (2, 1) ∈ R, but (1, 2) ∉ R
(iii) The relation on A having properties of being symmetric, reflexive and transitive is
R = {(1, 1), (2, 2), (3, 3), (4, 4), (1, 2), (2, 1)}
The relation R is an equivalence relation on A.
Example 9:. Show that the relation R defined by R = {(a, b): a – b is divisible by 3; a, b ∈ Z} is an equivalence relation.
Solution:
Given R = {(a, b): a – b is divisible by 3; a, b ∈ Z} is a relation
To prove equivalence relation it is necessary that the given relation should be reflexive, symmetric and transitive.
Let us check these properties on R.
Reflexivity:
Let a be an arbitrary element of R.
Then, a – a = 0 = 0 × 3
⇒ a − a is divisible by 3
⇒ (a, a) ∈ R for all a ∈ Z
So, R is reflexive on Z.
Symmetry:
Let (a, b) ∈ R
⇒ a − b is divisible by 3
⇒ a − b = 3p for some p ∈ Z
⇒ b − a = 3 (−p)
Here, −p ∈ Z
⇒ b − a is divisible by 3
⇒ (b, a) ∈ R for all a, b ∈ Z
So, R is symmetric on Z.
Transitivity:
Let (a, b) and (b, c) ∈ R
⇒ a − b and b − c are divisible by 3
⇒ a – b = 3p for some p ∈ Z
And b − c = 3q for some q ∈ Z
Adding the above two equations, we get
a − b + b – c = 3p + 3q
⇒ a − c = 3 (p + q)
Here, p + q ∈ Z
⇒ a − c is divisible by 3
⇒ (a, c) ∈ R for all a, c ∈ Z
So, R is transitive on Z.
Therefore R is reflexive, symmetric and transitive.
Hence, R is an equivalence relation on Z.
Example 10: Show that the relation R on the set Z of integers, given by
R = {(a, b): 2 divides a – b}, is an equivalence relation.
Solution:
Given R = {(a, b): 2 divides a – b} is a relation defined on Z.
To prove equivalence relation it is necessary that the given relation should be reflexive, symmetric and transitive.
Let us check these properties on R.
Reflexivity:
Let a be an arbitrary element of the set Z.
Then, a ∈ R
⇒ a − a = 0 = 0 × 2
⇒ 2 divides a − a
⇒ (a, a) ∈ R for all a ∈ Z
So, R is reflexive on Z.
Symmetry:
Let (a, b) ∈ R
⇒ 2 divides a − b
⇒ (a-b)/2 = p for some p ∈ Z
⇒ (b-a)/2 = – p
Here, −p ∈ Z
⇒ 2 divides b − a
⇒ (b, a) ∈ R for all a, b ∈ Z
So, R is symmetric on Z
Transitivity:
Let (a, b) and (b, c) ∈ R
⇒ 2 divides a−b and 2 divides b−c
⇒ (a-b)/2 = p and (b-c)/2 = q for some p, q ∈ Z
Adding the above two equations, we get
(a – b)/2 + (b – c)/2 = p + q
⇒ (a – c)/2 = p +q
Here, p+ q ∈ Z
⇒ 2 divides a − c
⇒ (a, c) ∈ R for all a, c ∈ Z
So, R is transitive on Z.
Therefore R is reflexive, symmetric and transitive.
Hence, R is an equivalence relation on Z.
Example 11:. Prove that the relation R on Z defined by (a, b) ∈ R ⇔ a − b is divisible by 5 is an equivalence relation on Z.
Solution:
Given relation R on Z defined by (a, b) ∈ R ⇔ a − b is divisible by 5
To prove equivalence relation it is necessary that the given relation should be reflexive, symmetric and transitive.
Let us check these properties on R.
Reflexivity:
Let a be an arbitrary element of R. Then,
⇒ a − a = 0 = 0 × 5
⇒ a − a is divisible by 5
⇒ (a, a) ∈ R for all a ∈ Z
So, R is reflexive on Z.
Symmetry:
Let (a, b) ∈ R
⇒ a − b is divisible by 5
⇒ a − b = 5p for some p ∈ Z
⇒ b − a = 5 (−p)
Here, −p ∈ Z [Since p ∈ Z]
⇒ b − a is divisible by 5
⇒ (b, a) ∈ R for all a, b ∈ Z
So, R is symmetric on Z.
Transitivity:
Let (a, b) and (b, c) ∈ R
⇒ a − b is divisible by 5
⇒ a − b = 5p for some Z
Also, b − c is divisible by 5
⇒ b − c = 5q for some Z
Adding the above two equations, we get
a −b + b − c = 5p + 5q
⇒ a − c = 5 ( p + q )
⇒ a − c is divisible by 5
Here, p + q ∈ Z
⇒ (a, c) ∈ R for all a, c ∈ Z
So, R is transitive on Z.
Therefore R is reflexive, symmetric and transitive.
Hence, R is an equivalence relation on Z.
Example 12:. Let n be a fixed positive integer. Define a relation R on Z as follows:
(a, b) ∈ R ⇔ a − b is divisible by n.
Show that R is an equivalence relation on Z.
Solution:
Given (a, b) ∈ R ⇔ a − b is divisible by n is a relation R defined on Z.
To prove equivalence relation it is necessary that the given relation should be reflexive, symmetric and transitive.
Let us check these properties on R.
Reflexivity:
Let a ∈ N
Here, a − a = 0 = 0 × n
⇒ a − a is divisible by n
⇒ (a, a) ∈ R
⇒ (a, a) ∈ R for all a ∈ Z
So, R is reflexive on Z.
Symmetry:
Let (a, b) ∈ R
Here, a − b is divisible by n
⇒ a − b = n p for some p ∈ Z
⇒ b − a = n (−p)
⇒ b − a is divisible by n [ p ∈ Z⇒ − p ∈ Z]
⇒ (b, a) ∈ R
So, R is symmetric on Z.
Transitivity:
Let (a, b) and (b, c) ∈ R
Here, a − b is divisible by n and b − c is divisible by n.
⇒ a − b= n p for some p ∈ Z
And b−c = n q for some q ∈ Z
a – b + b − c = n p + n q
⇒ a − c = n (p + q)
⇒ (a, c) ∈ R for all a, c ∈ Z
So, R is transitive on Z.
Therefore R is reflexive, symmetric and transitive.
Hence, R is an equivalence relation on Z.

 Carrier Point
Carrier Point
