Concepts of Planes and Cartesian and vector equation of a plane

Plane:

A plane is determined uniquely if any one of the following is known:

(i) the normal to the plane and its distance from the origin is given, i.e., equation of

a plane in normal form.

(ii) it passes through a point and is perpendicular to a given direction.

(iii) it passes through three given non collinear points.

Equation of a plane in normal form.:

Consider a plane whose perpendicular distance from the origin is d (d ¹ 0).

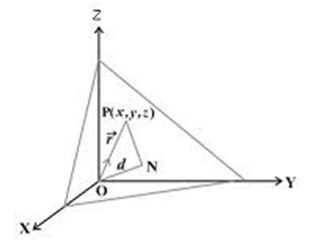
Cartesian form

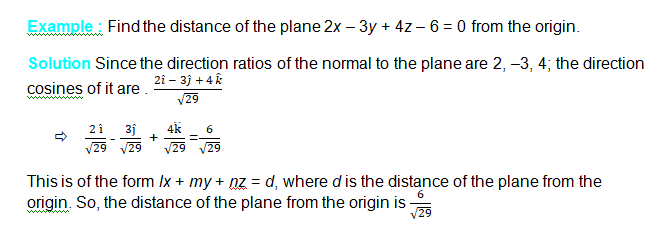
Example :Find the coordinates of the foot of the perpendicular drawn from the

origin to the plane 2x – 3y + 4z – 6 = 0.

Solution Let the coordinates of the foot of the perpendicular P from the origin to the

plane is (x1, y1,z1)

Then, the direction ratios of the line OP are

x1, y1, z1.

Since the direction ratios of the normal to the plane are 2, –3, 4;

Writing the equation of the plane in the normal

Note: If d is the distance from the origin and l, m, n are the direction cosines of the normal to the plane through the origin, then the foot of the perpendicular is (ld, md, nd).

Equation of a plane perpendicular to a given vector and passing through a given point:

Cartesian Form:

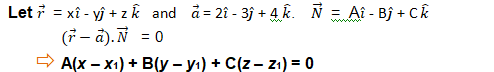
This is the cartesian equation of the plane.

Example : Find the vector and cartesian equations of the plane which passes through the point (5, 2, – 4) and perpendicular to the line with direction ratios 2, 3, – 1.

which is the Cartesian equation of the plane.

Equation of a plane passing through three non collinear points:

Let R, S and T be three non collinear points on the plane with position vectors

Respectively.

The vectors RS and RT are in the given plane. Therefore, the vector

is perpendicular to the plane containing points R, S and T. Let   be the position vector

of any point P in the plane. Therefore, the equation of the plane passing through R and perpendicular to the vector 

 

This is the equation of the plane in vector form passing through three non-collinear points.

Cartesian form

Let (x1, y1, z1), (x2, y2, z2) and (x3, y3, z3) be the coordinates of the points R, S and T respectively. Let (x, y, z) be the coordinates of any point P on the plane with position

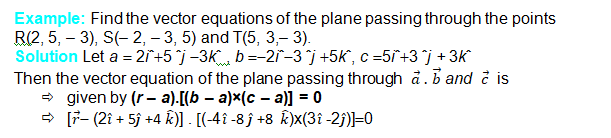
Intercept form of the equation of a plane:

Let the equation of the plane be

Ax + By + Cz + D = 0 (D ¹ 0) .................... (1)

Let the plane make intercepts a, b, c on x, y and z axes, respectively .

Hence, the plane meets x, y and z-axes at (a, 0, 0),(0, b, 0), (0, 0, c), respectively.

Plane passing through the intersection of two given planes:

Two planes can intersect in the three-dimensional space. Imagine two adjacent pages of a book. These two pages are nothing but an intersection of planes, intersecting each other and the line between them is called the line of intersection. A new plane i.e. a third plane can be given to be passing through this line of intersection of planes. We are to find out the equation of this plane.

Let us assume that the equation of the first plane is π1 and that of the second is π2. The equation of our required plane is π and we are to find out this equation itself. This equation is given by –

The position vector of any point on the line of intersection must

satisfy both the equations.

Vector form

If the equation of the two planes is given in Vector form –

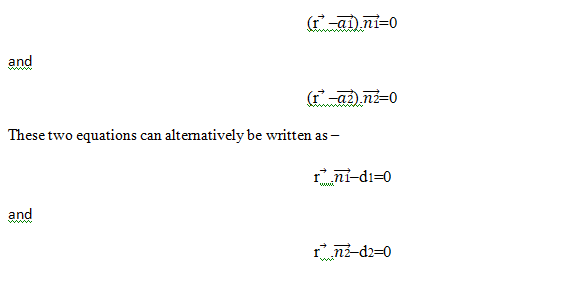
So the equation of the required plane by using (1) can be written as –

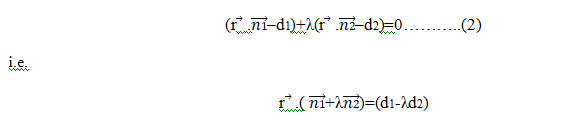
is equation of plane in vector form

Cartesian form:

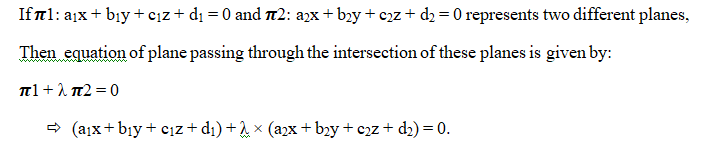
is equation of plane in cartesian form.

 

If a point on the required plane is given, you must substitute the coordinates for the values of x, y and z to obtain the value of λ in order to then replace it in the above equation. 

Question:

The equation of the plane passing through the intersection of the planes x+y+z=6 and 2x+3y+4z+5=0, and the point (1,1,1) is

Solution:

Given equation of planes are 

⇒x+y+z−6+λ(2x+3y+4z+5)=0
Given, it also passes through (1,1,1)
⇒1+1+1+−6+λ(2+3+4+5)=0⇒λ=143​
Hence, required plane is, 14(x+y+z−6)+3(2x+3y+4z+5)=0
⇒20x+23y+26z−69=0

Question:

The d.r's of the line of intersection of the planes x+y+z−1 =0 and 2x+3y+4z−7 =0 are