1. Direction cosines and direction ratios of a line joining two points.

Chapter 11

Three-Dimensional Geometry

Direction Cosines

In three-dimensional geometry, we have three axes: namely, the x, y, and z-axis. Let us assume a line OP passes through the origin in the three-dimensional space. Then, the line  will make an angle each with the x-axis, y-axis, and z-axis respectively.

The cosines of each of these angles  that the line makes with the x-axis, y-axis, and z-axis respectively are called direction cosines of the line in three-dimensional geometry. Normally, it is tradition to denote these direction cosines using the letters l, m, n respectively.

Note that these cosines can be found only once we have found the angles that the line makes with each of the axes. Also, it is interesting to note that if we reverse the direction of this line, the angles will obviously change.

Consequently, the direction cosines i.e. the cosines of these angles will also be different once the direction of the line is reversed. We will now look at a slightly different situation where our line does not pass through the origin (0,0,0).

1.Direction cosines and direction ratios of a line joining two points:

Let a line AB in 3D space make angles α, β, γ respectively with the +ve direction of coordinate axes X, Y, Z. Therefore, we express cosα, cosβ, cosγ as direction cosines of the line AB in the 3D space. Clearly; direction cosines fix the direction cosines of a line in space. Also, parallel lines have the same direction cosines. Direction cosines are denoted by l, m, n respectively. i.e. l = cosα, m = cosβ and n = cosγ. The direction of a line cannot be fixed in space by knowing anyone or any two angles.

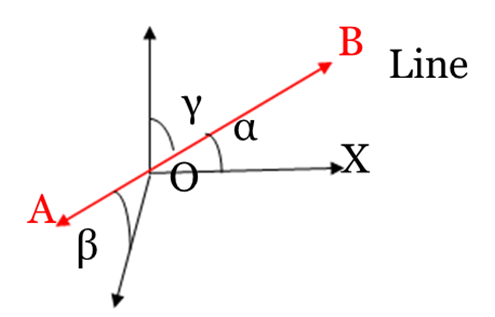
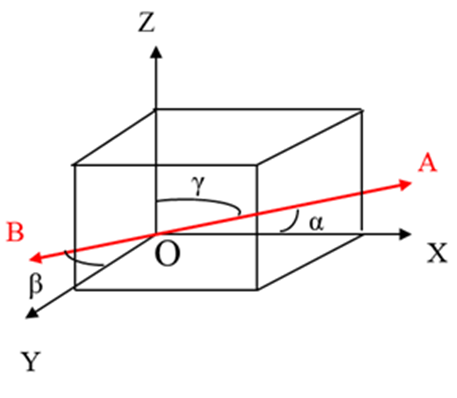
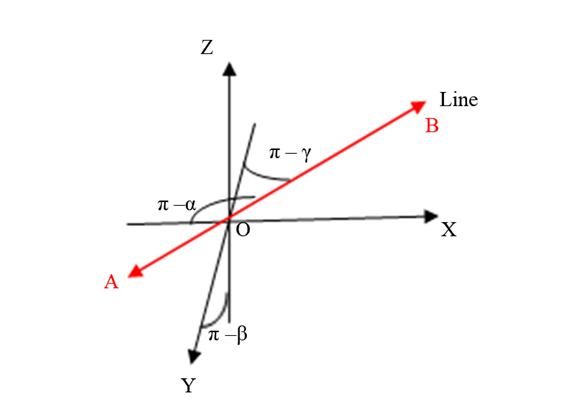
If a line in space makes angles α, β, γ respectively with the +ve direction of X, Y, Z axes then we can assume that the line will make angles π – α, π – β, π – γ with the -ve direction of axes. Therefore, the direction cosines can also be written as cos π -α, cos π -β, cos π –γ. Thus, direction cosines of the same line may also be taken as – cosα, –cosβ, –cosγ.

Three numbers a, b, c proportional to direction cosine l, m, n of a line in space. These numbers are called direction ratios OR direction numbers of the line. Therefore, the direction cosines of a line will be fixed but not the direction ratios:

Let direction cosine of any line in space be l, m, n and direction ratios(d.r.’s) are a:b:c.

Let P(x,y,z) be any point on the line and PM is perpendicular from P on X-axis. Then, in right triangle PMO,

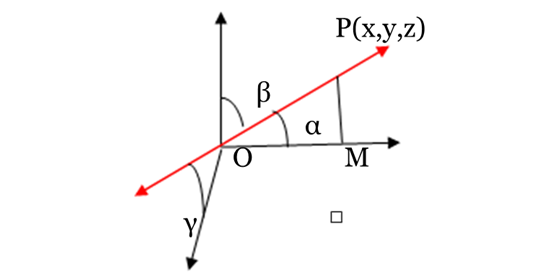
We can see that cos⁡α=OMOP=x/r . In this case x = OM and r = OP or l=x/r

Similarly, we take the perpendicular point P on y and axis to obtain: m=y/r ; n=z/r

Hence, we conclude that 

      r²=x²+y²+z²=(lr)²+(mr)²+(nr)²

• r²=[l²+m²+n²] r²
• l²+m²+n²=1

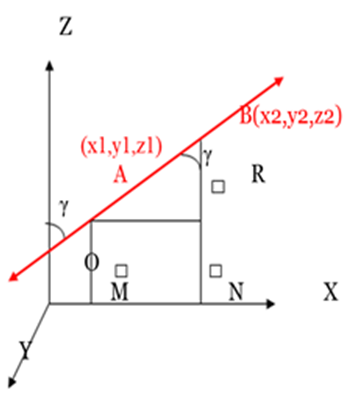
Let AB be a line that is inclined at angles α, β, γ with positive x, y, z-axis at points A (x1, y1, z1) and B at (x2, y2, z2) to form direction ratios. Line AB makes angle γ with the z-axis which is a part of a right angle triangle ∆ARB where,

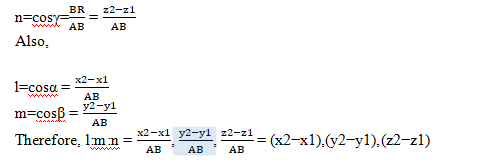
Solved Examples

Example : Find the direction ratios and direction cosines of a line joining the points (3, -4, 6) and (5, 2, 5).

Solution:

Given points are A(3, -4, 6) and B(5, 2, 5)

The direction ratios of the line joining AB is

a = x₂ – x₁ = 5 – 3 = 2

b = y₂ – y₁ = 2 + 4 = 6

c = z₂ – z₁ = 5 – 6 = -1

AB =

So direction cosines of the line = 2/√41, 6/√41, -1/√41.

Example : Find the direction cosines of the line joining the points (2,1,2) and (4,2,0).

Solution:

Let the points are A(2,1,2) and B(4,2,0).

x₂-x₁ = 4-2 = 2

y₂-y₁ = 2-1 = 1

z₂-z₁ = 0-2 = -2

AB = √(2²+1²+(-2)²)= 3

Hence the direction cosines are ⅔, ⅓, -⅔.

Example : Find the direction cosines of the line joining the points (2,3,-1) and (3,-2,1).

Solution:

Let the points are A(2,3,-1) and B(3,-2,1).

x₂-x₁ = 3-2 = 1

y₂-y₁ = -2-3 = -5

z₂-z₁ = 1- (-1) = 2

AB = √(1²+(-5)²+2²)= √30

Hence the direction cosines are 1/√30, -5/√30, 2/√30.