- Books Name
- Mathmatics Book Based on NCERT
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 12
- Subject
- Mathmatics
Chapter-4
Determinants
A determinant is a square array of numbers (written within a pair of vertical lines) which represents a certain sum of products. Below is an example of a 3 × 3 determinant (it has 3 rows and 3 columns). The result of multiplying out, then simplifying the elements of a determinant is a single number (a scalar quantity).
Concept of Determinant and Properties of Determinants:
A system of linear equations like
a1 x + b1 y = c1
a2 x + b2 y = c2
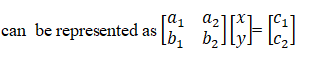
Now, this system of equations has a unique solution or not, is determined by the number.
a1 b2 – a2 b1 ( Recall that if
![]() or, a1 b2 – a2 b1 0, then the system of linear
or, a1 b2 – a2 b1 0, then the system of linear
equations has a unique solution). The number a1 b2 – a2 b1 which determines uniqueness of solution is associated with the matrix A = ![]()
and is called the determinant of A or det A.
Determinants have wide applications in Engineering, Science, Economics, Social Science, etc.
Determinant :
The determinant of a product of matrices is the product of their determinants (the preceding property is a corollary of this one). The determinant of a matrix A is denoted det(A), det A, or |A|.
In the case of a 2 × 2 matrix the determinant can be defined as
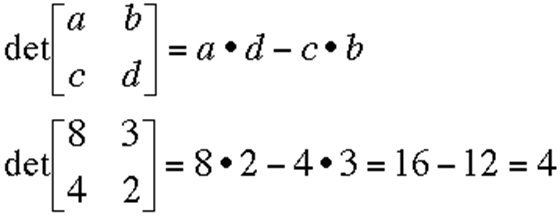
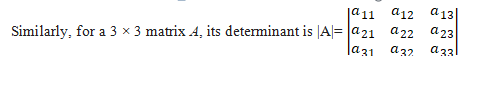
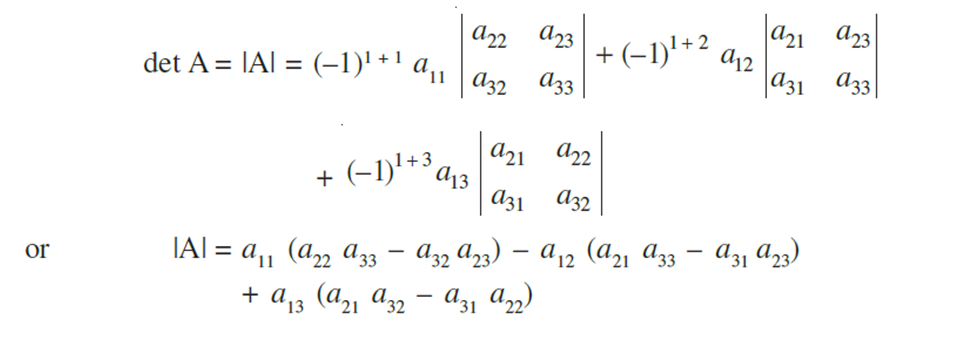
To every square matrix A = [aij] of order n, we can associate a number (real or complex) called determinant of the square matrix A, where a = (i, j)th element of A. This may be thought of as a function which associates each square matrix with a unique number (real or complex).
If M is the set of square matrices, K is the set of numbers (real or complex) and f : M → K is defined by f (A) = k, where A ∈ M and k ∈ K, then f (A) is called the determinant of A. It is also denoted by | A | or det A or Δ.

Properties of Determinants
Let us check the below seven properties of determinant in detail. The working principle and the formulas, explanation of each of the properties is also presented below.
1. Interchange Property
The value of a determinant remains unchanged if the rows or the columns of a determinant are interchanged.
Det(A) = Det(A')
It follows from this property that if the rows and columns of the matrix are interchanged, then the transpose of the matrix is obtained and the determinant value and the determinant of the transpose are equal.
2. Sign Property
The sign of the value of determinant changes if any two rows or any two columns are interchanged.
Det(A) = -Det(B)
The value of the determinant only changes the sign if the row or the column is swapped once. In the above matrix A, the second row has been swapped with the third row to obtain matrix B, and we have Det(A) = -Det(B). If the value of the determinant is D, and the rows or columns are swapped n times, then the new value of the determinant is (-1)nD.
3. Zero Property
The value of a determinant is equal to zero if any two rows or any two columns have the same elements.
Here the elements of the first row and the second row are identical. Hence the value of the determinant is equal to zero.
Det(A) = 0
4. Scalar Multiplication Property
The value of the determining becomes k times the earlier value of the determinant if each of the elements of a particular row or column is multiplied with a constant k.
Det(B) = k× Det(B)
The elements of the first row are multiplied with a constant k, and the determinant value is also multiplied with the constant k. This property helps in taking a common factor from each row or a column of the determinant. Also if the corresponding elements of any two rows or columns are equal then the value of the determinant is equal to zero.
5. Sum Property
If a few elements of a row or column are expressed as a sum of terms, then the determinant can be expressed as a sum of two or more determinants.
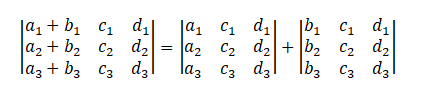
The elements of the first row represent the sum of terms, which can be split into two different determinants. Further, the new determinants also have the same second and third row, as the earlier determinant.
6. Property Of Invariance
If each element of a row and column of a determinant is added with the equimultiples of the elements of another row or column of a determinant, then the value of the determinant remains unchanged. This can be expressed in the form of a formula as Ri→Ri+kRj, or Ci→Ci+kCj.

The elements of the first row of matrix A have been replaced with the sum of the elements of the first row, and the third row multiplied with a constant, to obtain the new matrix B. Here, after this operation also, the determinant A is equal to determinant B.
7. Triangular Property
If the elements above or below the main diagonal are equal to zero, then the value of the determinant is equal to the product of the elements of the diagonal matrix.
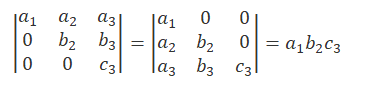
8. Factor Property:
If a determinant Δ becomes zero when we put
Then
is a factor of Δ.
9. Determinant of cofactor matrix:
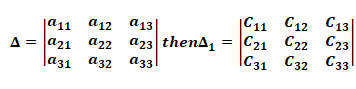
10. Switching Property:
The interchange of any two rows (or columns) of the determinant changes its sign.
Question : Using properties of determinants, prove that
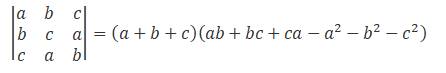
Solution:
By using invariance and scalar multiple property of determinant we can prove the given problem.
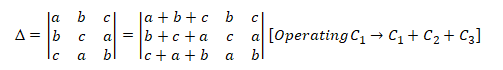
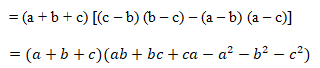
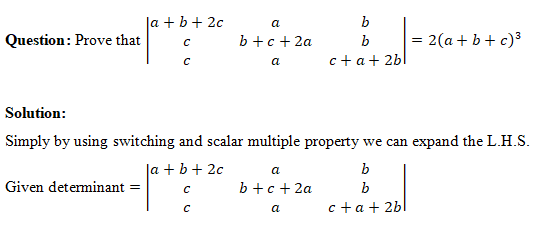
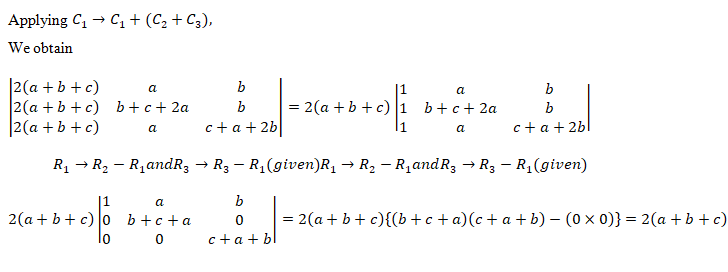

 KRISHNA PUBLICATIONS
KRISHNA PUBLICATIONS
