10. Mean Value Theorem

Mean Value Theorem:

 Rolle’s Theorem which states that:

Rolle’s Mean Value Theorem

If a function f  is defined in the closed interval [a, b] in such a way that it satisfies the following conditions.

i) The function f is continuous on the closed interval [a, b]

ii)The function  f is differentiable on the open interval (a, b)

iii) and  f (a) = f (b) ,

 then there exists at least one value of x=cÎ (a, b) such that f'(c) = 0.

Geometric interpretation of Rolle’s Theorem

 

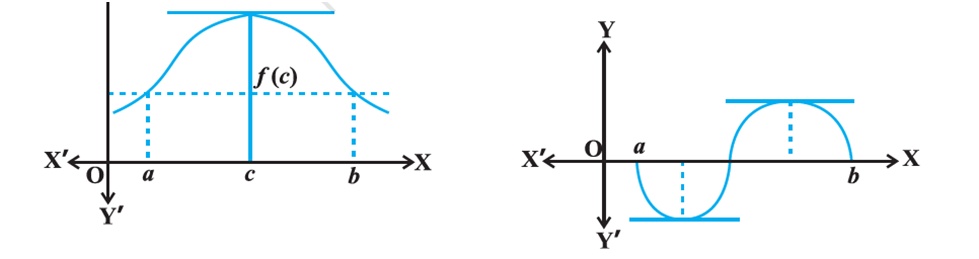
Observe what happens to the slope of the tangent to the curve at various points

between a and b. In each of the graphs, the slope becomes zero at least at one point.

That is precisely the claim of the Rolle’s theorem as the slope of the tangent at any

point on the graph of y = f (x) is nothing but the derivative of f (x) at that point.

Lagrange’s Mean Value Theorem (LMVT) 

Lagrange’s Mean Value Theorem or First Mean Value theorem states that a function f is defined in the closed interval [a, b], it satisfies the following conditions:

1. The function f is always continuous in the closed interval [a, b]
2. The function is always differentiable in the open interval (a, b)

 And there exists at least one value x = cÎ (a,b) such that,

[f(b)–f(a)]/ (b-a) = f’ (c)

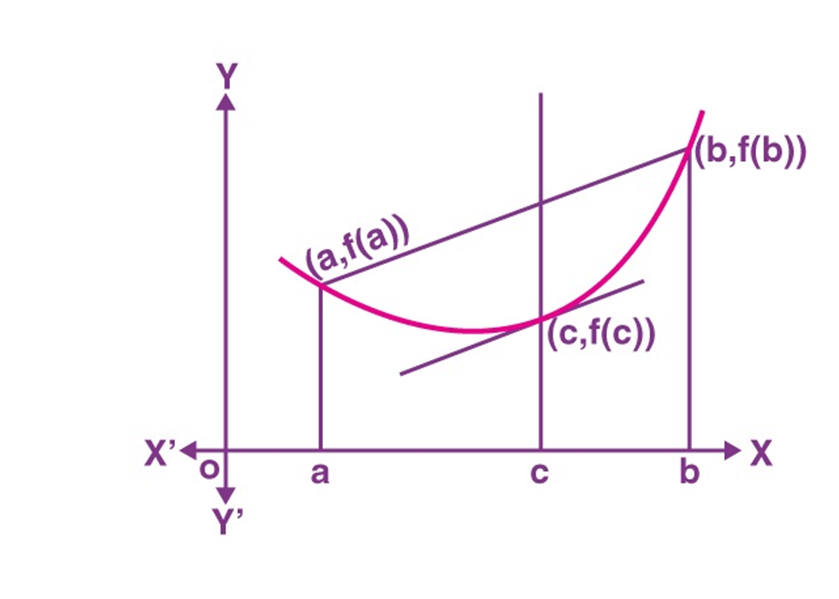
Geometrical Representation of Lagrange’s Mean Value Theorem

The graph given below the curve y = f(x) is  The function f  is

i) continuous on the closed interval [a, b]

ii)The function f  is differentiable on the open interval (a, b)

then, According to the Lagrange Mean Value Theorem, 

Any function that is continuous on [a,b] and also differentiable on (a,b) has some in the interval (a,b) such that the secant joining the interval's ends is parallel to the tangent at point C.

f ’(c) = [ f (b) –f (a)]/(b-a)

Example:

Verify Mean Value Theorem for the function  f(x) = x² – 4x – 3 in the interval [a, b], where a = 1 and b = 4.

Solution:

Given,

f(x) = x² – 4x – 3

f'(x) = 2x – 4

a = 1 and b = 4 (given)

f(a) = f(1) = (1)² – 4(1) – 3 = 1 – 4 – 3 = -6

f(b) = f(4) = (4)² – 4(4) – 3 = -3

Now,

[f(b) – f(a)]/ (b – a) = (-3 + 6)/(4 – 1) = 3/3 = 1

As per the Lagrange’s mean value theorem statement, there is a point c ∈ (1, 4) such that

 f'(c) = [f(b) – f(a)]/ (b – a),

i.e. f'(c) = 1.

2c – 4 = 1

2c = 5

c = 5/2 ∈ (1, 4)

Verification: f'(c) = 2(5/2) – 4 = 5 – 4 = 1

Hence, verified the mean value theorem.

Example: 

Verify Rolle’s theorem for the function y = x² + 2, a = –2 and b = 2.

Solution:

From the definition of Rolle’s theorem, the function y = x² + 2 is continuous in [– 2, 2] and differentiable in (– 2, 2).

From the given,

f(x) = x² + 2

f(-2) = (-2)² + 2 = 4 + 2 = 6

f(2) = (2)² + 2 = 4 + 2= 6

Thus, f(– 2) = f( 2) = 6

Hence, the value of f(x) at –2 and 2 coincide.

Now, f'(x) = 2x 

Rolle’s theorem states that there is a point c ∈ (– 2, 2) such that f′(c) = 0. 

At c = 0, f′(c) = 2(0) = 0, where c = 0 ∈ (– 2, 2)

Hence verified.