1. Conditional probability

Chapter 13

Probability

1.Conditional probability:

If E and F are two events associated with the same sample space ‘S’ of a random experiment,

The conditional probability of E given that F has already occurred,

Note that (1) is valid only when P(F) ≠ 0 i.e., F ≠ φ (Why?)

 P(A|B) is the probability of event A occurring, given that event B occurs.

For example, given that you drew a red card,

what's the probability that it's a four (p(four|red))=2/26=1/13.

So out of the 26 red cards (given a red card), there are two fours

= 2/26=1/13.

Properties of conditional probability:

 Let E and F be events of a sample space S of an experiment, then we have

Property 1.

 P(S|F) = P(F|F) = 1

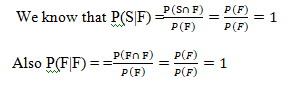
Thus P(S|F) = P(F|F) = 1

Property 2.

 If A and B are any two events of a sample space S and F is an event of S such that P(F) ≠ 0,

then P((A ∪ B)|F) = P(A|F) + P(B|F) – P((A ∩ B)|F)

 if A and B are disjoint events, then P((A∪B)|F) = P(A|F) + P(B|F)

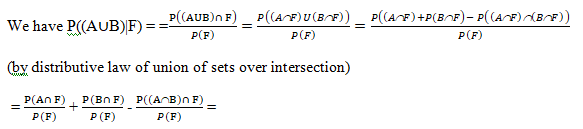
= P(A|F) + P(B|F) – P((A ∩B)|F)

When A and B are disjoint events, then P((A ∩ B)|F) = 0

 ⇒ P((A ∪ B)|F) = P(A|F) + P(B|F)

Property 3.

 P(E′|F) = 1 − P(E|F) From Property 1,

we know that P(S|F) = 1 ⇒ P(E ∪ E′|F) = 1

since S = E ∪ E′ ⇒ P(E|F) + P (E′|F) = 1

 since E and E′ are disjoint events

Thus, P(E′|F) = 1 − P(E|F)

Example 1.:  If P(A) = 7 13 , P(B) = 9 13 and P(A ∩ B) = 4 13 , evaluate P(A|B).

Solution:

Example 2.:  A family has two children. What is the probability that both the children are boys given that at least one of them is a boy ?

Solution:  Let b stand for boy and  g for girl.

The sample space of the experiment is S = {(b, b), (g, b), (b, g), (g, g)}

 Let E and F denote the following events :

 E : ‘both the children are boys’

F : ‘at least one of the child is a boy’

Then E = {(b,b)}  and  F = {(b,b), (g,b), (b,g)}

 Now E ∩ F = {(b,b)}

Thus P(F) = 3/ 4 and P (E ∩ F )= 1/ 4

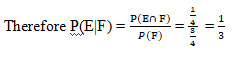
Example 3:  Consider the experiment of tossing a coin. If the coin shows head, toss it again but if it shows tail, then throw a die. Find the conditional probability of the event that ‘the die shows a number greater than 4’ given that ‘there is at least one tail’.

Solution:  S = {(H,H), (H,T), (T,1), (T,2), (T,3), (T,4), (T,5), (T,6)}

Let F be the event that ‘there is at least one tail’ and

    E be the event ‘the die shows a number greater than 4’.

Then F = {(H,T), (T,1), (T,2), (T,3), (T,4), (T,5), (T,6)}

E = {(T,5), (T,6)} and

E ∩ F = {(T,5), (T,6)}

Now P(F) = P({(H,T)}) + P ({(T,1)}) + P ({(T,2)}) + P ({(T,3)}) + P ({(T,4)}) + P({(T,5)}) + P({(T,6)})

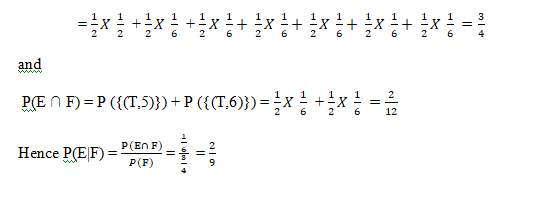
Example 1: Two dies are thrown simultaneously, and the sum of the numbers obtained is found to be 7. What is the probability that the number 3 has appeared at least once?

Solution: The sample space S would consist of all the numbers possible by the combination of two dies. Therefore S consists of 6 × 6, i.e. 36 events.

Event A indicates the combination in which 3 has appeared at least once.

Event B indicates the combination of the numbers which sum up to 7.

A = {(3, 1), (3, 2), (3, 3)(3, 4)(3, 5)(3, 6)(1, 3)(2, 3)(4, 3)(5, 3)(6, 3)}

B = {(1, 6)(2, 5)(3, 4)(4, 3)(5, 2)(6, 1)}

P(A) = 11/36

P(B) = 6/36

A ∩ B = 2

P(A ∩ B) = 2/36

Applying the conditional probability formula we get,

P(A|B) = P(A∩B)/P(B) = (2/36)/(6/36) = ⅓

Example 2: In a group of 100 computer buyers, 40 bought CPU, 30 purchased monitor, and 20 purchased CPU and monitors. If a computer buyer chose at random and bought a CPU, what is the probability they also bought a Monitor?

Solution: As per the first event, 40 out of 100 bought CPU,

So, P(A) = 40% or 0.4

Now, according to the question, 20 buyers purchased both CPU and monitors. So, this is the intersection of the happening of two events. Hence,

P(A∩B) = 20% or 0.2

By the formula of conditional probability we know;

P(B|A) = P(A∩B)/P(B)

P(B|A) = 0.2/0.4 = 2/4 = ½ = 0.5

The probability that a buyer bought a monitor, given that they purchased a CPU, is 50%.