1. Area under Simple Curves especially lines, circles/ parabolas/ellipses (in standard form only)

Chapter 8

Area under Simple Curves especially lines, circles/ parabolas/ellipses (in standard form

One of the major application of integrals is in determining the area under the curves.

Consider a function y = f(x), then the area is given as

 

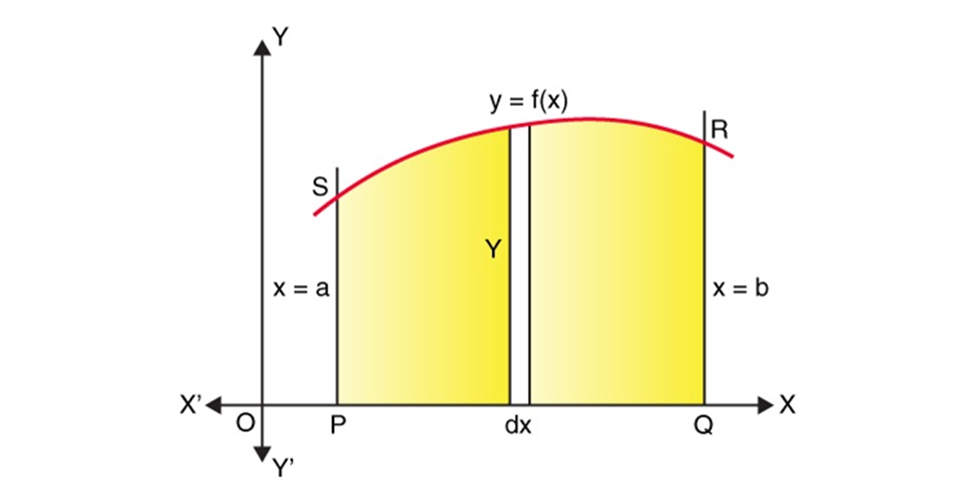
Consider the two curves having equation of f(x) and g(x), the area between the region a,b of the two curves is given as-

dA = f(x) – g(x)]dx, and the total area A can be taken as-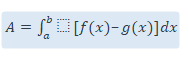

Application of Integrals Examples

Example 1: 

Determine the area enclosed by the circle x² + y² = a²

Solution:

Given, circle equation is x² + y² = a²

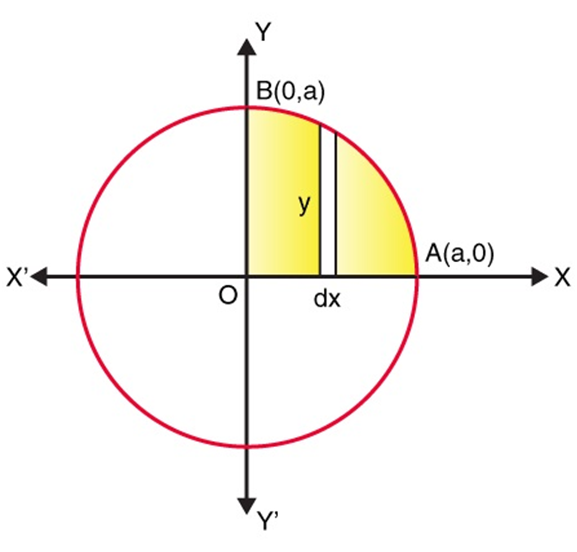
From the given figure, we can say that the whole area enclosed by the given circle is as

= 4(Area of the region AOBA bounded by the curve, coordinates x=0 and x=a, and the x-axis)

As the circle is symmetric about both x-axis and y-axis, the equation can be written as 

= 4 ₀∫^a y dx (By taking the vertical strips) ….(1)

From the given circle equation, y can be written as

y = ±√(a²-x²)

As the region, AOBA lies in the first quadrant of the circle, we can take y as positive, so the value of y becomes √(a²-x²)

Now, substitute y = √(a²-x²) in equation (1), we get

= 4 ₀∫^a √(a²-x²) dx 

Integrate the above function, we get

= 4 [(x/2)√(a²-x²) +(a²/2)sin^-1(x/a)]₀ ^a

Now, substitute the upper and lower limit, we get

= 4[{(a/2)(0)+(a²/2)sin^-1 1}-{0}]

= 4(a²/2)(π/2)

= πa².

Hence, the area enclosed by the circle x² +y² =a²  is πa².