1. Basic Concepts of Differential Equations and Types of Differential equations
- Books Name
- Mathmatics Book Based on NCERT
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 12
- Subject
- Mathmatics
Chapter 9
Differential Equations
Basic Concepts of Differential Equations and Types of Differential equations
Differential Equations:
A differential equation is any equation which contains derivatives, either ordinary derivatives or partial derivatives.
Example:
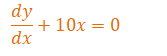
Example:
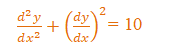
Differential equation into two types:
- Ordinary differential equation
- partial differential equations.
[1] Ordinary differential equation:
An ordinary differential equation is an equation which is defined for one or more functions of one independent variable and its derivatives. It is abbreviated as ODE.
y'=x+1 is an example of ODE.
An ordinary differential equation is a differential equation that does not involve partial derivatives
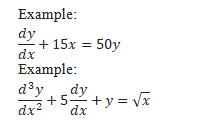
[2] partial differential equations. :
A partial differential equation (or briefly a PDE) is a mathematical equation that involves two or more independent variables, an unknown function (dependent on those variables), and partial derivatives of the unknown function with respect to the independent variables.
A partial differential equation is a differential equation that involves partial derivatives.
Example:
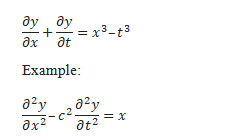
2. Order and Degree of a differential equation
- Books Name
- Mathmatics Book Based on NCERT
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 12
- Subject
- Mathmatics
Order and Degree of a differential equation
What is ODE and PDE?
Ordinary differential equations or (ODE) are equations where the derivatives are taken with respect to only one variable. That is, there is only one independent variable. Partial differential equations or (PDE) are equations that depend on partial derivatives of several variables.
Order of differential equation
The highest order of the derivative present in the dependent variable with respect to the independent variable in the given differential equation is called order of DE.
Degree of differential equation
Degree of the differential equation is the exponent of the highest derivative of the differential equation
Example:
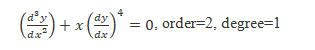
Example:
![]()
order=2, degree=not defined because it is not a polynomial function.
Example:
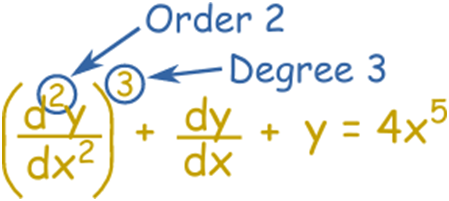
order=2 ,degree=3
Example :
![]()
Here, the exponent of the highest order derivative is one and the given differential equation is a polynomial equation in derivatives. Hence, the degree of this equation is 1.
Example :
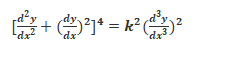
The order of this equation is 3 and the degree is 2 as the highest derivative is of order 3 and the exponent raised to the highest derivative is 2.
Order and degree (if defined) of a differential equation are always positive integers.
3. General and Particular Solutions of a Differential Equation
- Books Name
- Mathmatics Book Based on NCERT
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 12
- Subject
- Mathmatics
General and Particular Solution of a Differential Equation
General(or primitive) solution:
The solution which contains arbitrary constants is called the general(or primitive) solution of the differential equation.
The general solution of the differential equation is of the form y = f(x) or y = ax + b and it has a, b as its arbitrary constants.
Example:
The function y = a cos x + b sin x, where, a, b Î R is a solution
of the differential equation
![]()
Particular solution:
The solution free from arbitrary constants obtained from the general solution by giving particular values to the arbitrary constants is called a particular solution of the differential equation.
Example: y = e– 3x is a particular solution of the differential equation
![]()
Example : The number of arbitrary constants in the general solution of a differential equation
of fourth order are:
- 0
- 2
- 3
- 4
Ans: D
Example: The number of arbitrary constants in the particular solution of a differential equation
of third order are:
- 3
- 2
- 1
- 0
Ans: D
4. Formation of a Differential Equation whose General Solution is given
- Books Name
- Mathmatics Book Based on NCERT
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 12
- Subject
- Mathmatics
Formation of a Differential Equation whose General Solution is given
The order of a differential equation representing a family of curves is the same as the number of arbitrary constants present in the equation corresponding to the family of curves.
Procedure to form a differential equation that will represent a given
family of curves:
(a) If the given family F1 of curves depends on only one parameter then it is
represented by an equation of the form
F1 (x, y, a) = 0 ... (1)
For example, the family of parabolas y2 = ax can be represented by an equation of the form
f (x, y, a) : y2 = ax.
Differentiating equation (1) with respect to x, we get an equation involving y', y, x, and a,
i.e.,
g (x, y, y', a) = 0 ................ (2)
The required differential equation is then obtained by eliminating a from equations (1) and (2) as
F(x, y, y' ) = 0 ..................... (3)
(b) If the given family F2 of curves depends on the parameters a, b (say) then it is represented by an equation of the from
F2 (x, y, a, b) = 0 …………………….(4)
Differentiating equation (4) with respect to x, we get an equation involving ![]() , x, y, a, b,
, x, y, a, b,
i.e.,
g (x, y, y'', a, b) = 0 ………………………(7)
But it is not possible to eliminate two parameters a and b from the two equations and so, we need a third equation. This equation is obtained by differentiating equation (5), with respect to x, to obtain a relation of the form
h (x, y, y',
The required differential equation is then obtained by eliminating a and b from equations (4), (5) and (6) as
F (x, y, y',
Note: The order of a differential equation representing a family of curves is same as the number of arbitrary constants present in the equation corresponding to the family of curves.
Example : Form the differential equation representing the family of curves y = mx,
where, m is arbitrary constant.
Solution: We have
y = mx ... …………………(1)
Differentiating both sides of equation (1) with respect to x, we get
y’ = m
Substituting the value of m in equation (1) we get
y= y’ x
- xy’-y=0
which is free from the parameter m and hence this is the required differential equation.
Example : Form the differential equation representing the family of curves
y = a sin (x + b), where a, b are arbitrary constants.
Solution :We have
y = a sin (x + b) ... ……………(1)
Differentiating both sides of equation (1) with respect to x, successively we get
y’ =a cos(x+b)…………………..(2)
- y’’ = -a sin(x+b)………………….(3)
Eliminating a and b from equations (1), (2) and (3), we get
y’’ +y =0 ………………………(4)
which is free from the arbitrary constants a and b and hence this the required differential equation.
5. Methods of Solving First Order, First Degree Differential Equations and Differential equations with variables separable
- Books Name
- Mathmatics Book Based on NCERT
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 12
- Subject
- Mathmatics
Methods of Solving First Order, First Degree Differential Equations
There are three methods to solve the first-order, first-degree differential equations. They are:
- Differential equations with variables separable
- Homogeneous differential equations
- Linear differential equations
Differential equations with variables separable:
A first order-first degree differential equation is of the form

If F (x, y) can be expressed as a product g (x) h(y), where, g(x) is a function of x and h(y) is a function of y, then the differential equation (1) is said to be of variable separable type. The differential equation (1) then has the form
![]()
If h (y) ¹0, separating the variables, (2) can be rewritten as
![]()
Integrating both sides of (3), we get
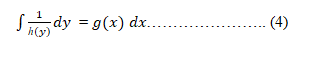
Thus, (4) provides the solutions of given differential equation in the form
H(y) = G(x) + C
Example: Find the general solution of the differential equation ![]()
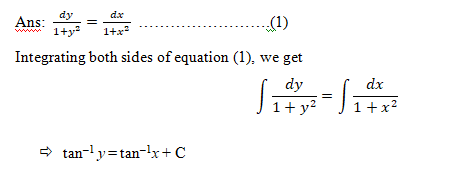
which is the general solution of equation (1).
6. Solutions of homogeneous differential equations of first order and first degree
- Books Name
- Mathmatics Book Based on NCERT
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 12
- Subject
- Mathmatics
Homogeneous differential equations
A function F(x, y) is said to be homogeneous function of degree n if
F(λx, λy) = λnF(x, y) for any nonzero constant λ .
A differential equation of the form ![]() is said to be homogenous if F(x, y) is a homogenous function of degree zero. We make the substitution y = v . x
is said to be homogenous if F(x, y) is a homogenous function of degree zero. We make the substitution y = v . x
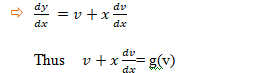
Separating the variables in equation , we get

Integrating both sides of equation (5), we get

Equation (6) gives general solution (primitive) of the differential equation (1) when
we replace v by y/x.
Example: Solve dy/dx = (x-y)/(x+y)
Solution: Given, dy/dx = (x-y)/(x+y)
It is homogeneous degree 0.
![]()
Then,
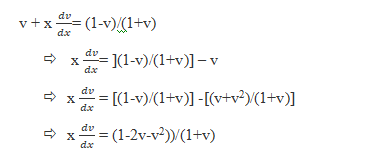
Now we can use the separation of variables method;
(1+v)/(1-2v-v2) dv = (1/x) dx
Integrating both the sides;
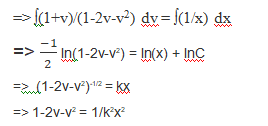
Again, putting v = y/x;
1-2(y/x)-(y/x)2 = 1/k2x2
Eliminating x2 term from denominator on both the sides, we get;
x2-2xy-y2 = 1/k2
or
y2+2xy-x2 = -1/k2
Now, put -/k2 = c
Adding 2x2 on both the sides;
y2+2xy+x2 = c+2x2
Now factoring the above equation, we get;
(y+x)2 = 2x2+c
y+x=√(2x2)+c
Or y = ±√(2x2+c) − x
This is the solution for the given equation.
Example: Find the equation of the curve passing through the point (1,-2) when the tangent at any point is given by ![]()
Solution: The equation of tangent represents the slope of the curve i.e.
This equation is homogeneous in nature.
On cross-multiplication, we get- ![]()
Solving the equation, we get
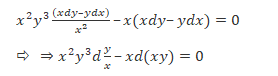
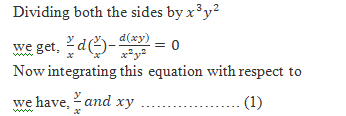
Now substituting the value of the given point in the above equation, we have
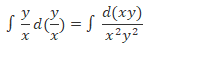
Put this value of the constant C in equation (1) we get
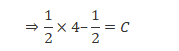
This is the required solution.
7. Solutions of linear differential equation of first order and first degree
- Books Name
- Mathmatics Book Based on NCERT
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 12
- Subject
- Mathmatics
Solutions of linear differential equation of first order and first degree
[1] A differential equation of the from
![]()
Where p,q are constants or functions of x, is known as a first order linear differential equation.
Integrating Factor(I.F.) of the given differential equation = g(x) ![]()
Write the solution of the given differential equation as
The general solution of the given differential equation as
![]()
[2] A differential equation of the from
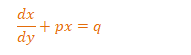
Where p,q are constants or functions of y, is known as a first order linear differential equation.
![]()
Write the solution of the given differential equation as
The general solution of the given differential equation as
![]()
Example :
Solve the following differential equation:

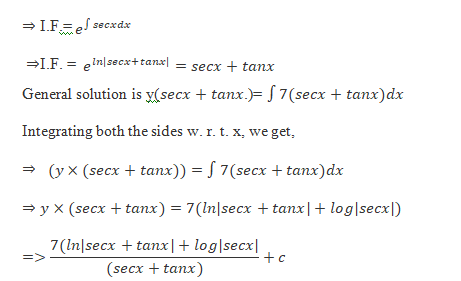
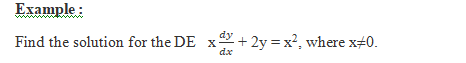
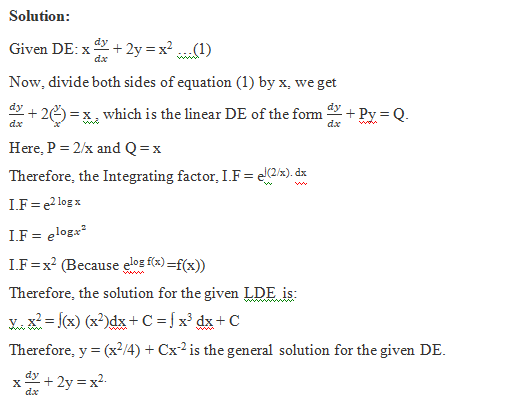

 KRISHNA PUBLICATIONS
KRISHNA PUBLICATIONS
