4. One-one(injective) functions, onto (surjective) functions, bijective functions.

Types of Functions

One to one Function: A function f : X → Y is defined to be one-one (or injective), if the images of distinct elements of X under f are distinct,

i.e., for every x₁ , x₂ ∈ X, f(x₁ ) = f(x₂ ) implies x₁ = x₂ . Otherwise, f is called many-one.

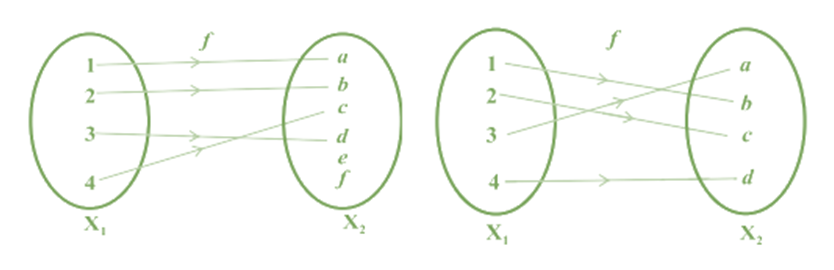
Examples

Examples of one-one / injective Function

• The identity function X → X is always one-one.
• If function f: R→ R, then f(x) = 2x is one-one.
• If function f: R→ R, then f(x) = 2x+1 is one-one.
• If function f: R→ R, then f(x) = x² is not an injective function, because here

if x = -1, then f(-1) = 1 = f(1). Hence, the element of co-domain is not discrete here.

• If function f: R→ R, then f(x) = x/2 is one-one.
• If function f: R→ R, then f(x) = x³ is one-one.
• If function f: R→ R, then f(x) = 4x+5 is one-one.

Properties of One-One Function

• If f and g are both one to one, then f ∘ g follows one-one.
• If g ∘ f is one to one, then function f is one to one, but function g may not be.
• f: X → Y is one-one, if and only if, given any functions g, h : P → X whenever f ∘ g = f ∘ h, then g = h..
• If f: X → Y is one-one and P is a subset of X, then f^-1 (f(A)) = P. Thus, P can be retrieved from its image f(P).
• If f: X → Y is one-one and P and Q are both subsets of X, then f(P ∩ Q) = f(P) ∩ f(Q).
• If both X and Y are limited with the same number of elements, then f: X → Y is one-one, if and only if f is surjective or onto function.

Example :

Show that f: R→ R defined as f(a) = 3x³ – 4 is one to one function?

Solution:

Let f ( x₁ ) = f ( x₂ ) for all a₁ , a₂ ∈ R

•  3x₁³ – 4 = 3x₂³ – 4
• x₁³ = x₂³ 
• x₁³ – x₂³ = 0
• (x₁ – x₂) (x₁ + x₁x₂ + x₂²) = 0
• x₁ = x₂ and (x₁² + x₁x₂ + x₂²) = 0 
• (x₁² + x₁x₂ + x₂²) = 0 is not considered because there are no real values of x₁ and x₂.

Therefore,  the given function f is one-one.

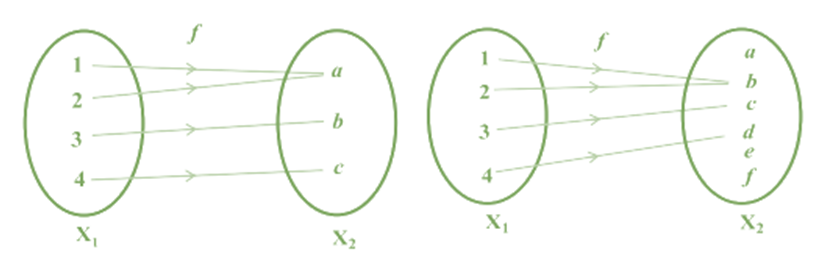
1. Onto Function: A function f: X → Y is said to be onto (or surjective), if every element of Y is the image of some element of X under f,(Codomain=Range)

i.e., for every y ∈ Y, there exists an element x in X such that f(x) = y.