1. Concept of Integrals and types of integral
- Books Name
- Mathmatics Book Based on NCERT
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 12
- Subject
- Mathmatics
Chaper 7
Integrals
Integration is the act of bringing together smaller components into a single system that functions as one.
Differentiation is the process of finding the derivative of the functions and integration is the process of finding the antiderivative of a function. So, these processes are inverse of each other. So we can say that integration is the inverse process of differentiation or vice versa. The integration is also called the anti-differentiation. In this process, we are provided with the derivative of a function and asked to find out the function (i.e., primitive).
To represent the antiderivative of “f”, the integral symbol “∫” symbol is introduced. The antiderivative of the function is represented as ∫ f(x) dx. This can also be read as the indefinite integral of the function “f” with respect to x.
Therefore, the symbolic representation of the antiderivative of a function (Integration) is:
y = ∫ f(x) dx
y=∫ f(x) dx = F(x) + C.
Types of Integrals
Two types of integrals in maths:
- Definite Integral
- Indefinite Integral
Definite Integral
An integral that contains the upper and lower limits then it is a definite integral. On a real line, x is restricted to lie. Riemann Integral is the other name of the Definite Integral.
A definite Integral is represented as:
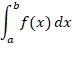
Indefinite Integral
Indefinite integrals are defined without upper and lower limits. It is represented as:
∫f(x)dx = F(x) + C
Where C is any constant and the function f(x) is called the integrand.
Properties Indefinite Integral:
1.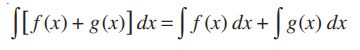
2.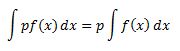 or
or
![]()
3. For a finite number of functions f1, f2…. fn and the real numbers p1, p2…pn,
∫[p1f1(x) + p2f2(x)….+pnfn(x) ]dx = p1∫f1(x)dx + p2∫f2(x)dx + ….. + pn∫fn(x)dx
2. Integration as an Inverse Process of Differentiation
- Books Name
- Mathmatics Book Based on NCERT
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 12
- Subject
- Mathmatics
Integration as an Inverse Process of Differentiation

Example : Find the anti derivative F of f defined by f (x) = 4x3 – 6, where F (0) = 3
Solution: One anti derivative of f (x) is x4 – 6x since
![]()
Therefore, the anti derivative F is given by
F(x) = x4 – 6x + C, where C is constant.
Given that F(0) = 3, which gives,
3 = 0 – 6 0 + C or C = 3
Hence, the required anti derivative is the unique function F defined by
F(x) = x4 – 6x + 3.
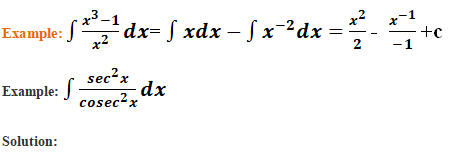
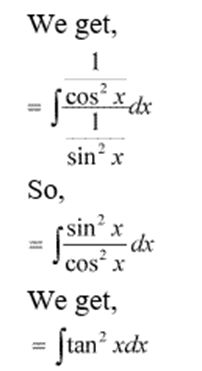
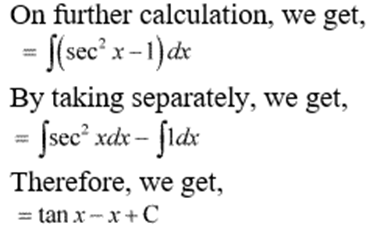
3. Geometrical interpretation and Some properties of indefinite integral
- Books Name
- Mathmatics Book Based on NCERT
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 12
- Subject
- Mathmatics
Geometrical interpretation and Some properties of indefinite integral
Comparison between differentiation and integration
1. Both are operations on functions.
2. Both satisfy the property of linearity, i.e.,
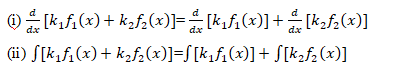
Here k1 and k2 are constants.
3. We have already seen that all functions are not differentiable. Similarly, all functions
are not integrable. We will learn more about nondifferentiable functions and
nonintegrable functions in higher classes.
4. The derivative of a function, when it exists, is a unique function. The integral of
a function is not so. However, they are unique upto an additive constant, i.e., any
two integrals of a function differ by a constant.
5. When a polynomial function P is differentiated, the result is a polynomial whose
degree is 1 less than the degree of P. When a polynomial function P is integrated,
the result is a polynomial whose degree is 1 more than that of P.
6. We can speak of the derivative at a point. We never speak of the integral at a
point, we speak of the integral of a function over an interval on which the integral
is defined .
7. The derivative of a function has a geometrical meaning, namely, the slope of the
tangent to the corresponding curve at a point. Similarly, the indefinite integral of a function represents geometrically, a family of curves placed parallel to each other having parallel tangents at the points of intersection of the curves of the family with the lines orthogonal (perpendicular) to the axis representing the variable
of integration.
8. The derivative is used for finding some physical quantities like the velocity of a
moving particle, when the distance traversed at any time t is known. Similarly,
the integral is used in calculating the distance traversed when the velocity at time
t is known.
9. Differentiation is a process involving limits. So is integration.
10.The process of differentiation and integration are inverses of each other .
Types of Integration Maths or the Integration Techniques:-
- Integration by Inspection.
- Integration by Substitution.
- Integration by Parts.
- Integration by Partial Fraction.
Integration by Inspection:
Example: Solve ![]()
Example : Find the anti derivative F of f defined by f (x) = 4x3 – 6, where F (0) = 3
Solution: One anti derivative of f (x) is x4 – 6x since
![]()
Therefore, the anti derivative F is given by
F(x) = x4 – 6x + C, where C is constant.
Given that F(0) = 3, which gives,
3 = 0 – 6 0 + C or C = 3
Hence, the required anti derivative is the unique function F defined by
F(x) = x4 – 6x + 3.
Example:
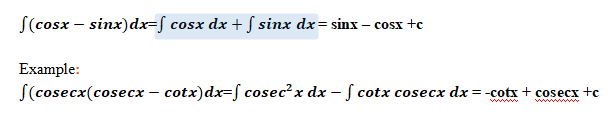
4. Methods of Integration(Integration by substitution)
- Books Name
- Mathmatics Book Based on NCERT
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 12
- Subject
- Mathmatics
Integration by Substitution:
Integration by substitution, also known as u-substitution, reverse chain rule or change of variables, is a method for evaluating integrals and antiderivatives. It is the counterpart to the chain rule for differentiation, and can loosely be thought of as using the chain rule "backwards".
The General Form of integration by substitution is:
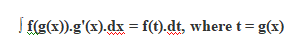
Usually the method of integration by substitution is extremely useful when we make a substitution for a function whose derivative is also present in the integrand. Doing so, the function simplifies and then the basic formulas of integration can be used to integrate the function.
Example:
∫sin (x3).3x2.dx = ∫sin t . dt Let x3= t => 3x2dx =dt
= -cos t + c
Example :
Find the integration of
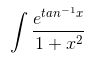
Solution:
Given : I =
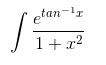
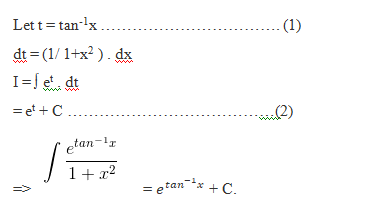
Example :
Integrate 6x cos (x2 – 5) with respect to x .
Solution:
I = ∫6xcos(x2 – 5).dx
Let x2 – 5 = t …..(1)
2x.dx = dt
we have
I = 3∫cos(t).dt
= 3sin t + c …..(2)
= 3sin (x2 – 5) + C
![]()
We know that tan x = sin x / cos x.
Therefore,
∫ tan x dx = ∫ (sin x / cos x) dx.
Now, let cos x = t, => sin x dx = – dt.
Therefore,
∫ tan x dx = – ∫ (dt / t) = – log |cos x| + C
Or, ∫ tan x dx = log |sec x| + C
![]()
We know that cot x = cos x / sin x. Therefore,
∫ cot x dx = ∫ (cos x / sin x) dx.
Now, let sin x = t, => cos x dx = – dt.
Therefore,
∫ cot x dx = ∫ (dt / t) = log |t| + C = log |sin x| + C
![]()
On multiplying both the numerator and denominator by (sec x + tan x), we have
∫ sec x dx = ∫ {sec x (sec x + tan x) dx} / (sec x + tan x)
Now, let (sec x + tan x) = t, => sec x (sec x + tan x) dx = dt.
Therefore, ∫ sec x dx = ∫ (dt / t) = log |t| + C = log |sec x + tan x| + C
![]()
On multiplying both the numerator and denominator by (cosec x + cot x), we have
∫ cosec x dx = ∫ {cosec x (cosec x + cot x) dx} / (cosec x + cot x)
Now, let (x + cot x) = t, => – cosec x (cosec x + cot x) dx = dt.
Therefore, ∫ cosec x dx = – ∫ (dt / t) = – log |t| + C = – log |cosec x + cot x| + C
= – log |(cosec2 x – cot2 x) / (cosec x – cot x)| + C
= log |cosec x – cot x| + C
Example :
Find the integral of (sin3 x) (cos2 x) dx
Solution: We have,
∫ (sin3 x) (cos2 x) dx = ∫ (sin2 x) (cos2 x) (sin x) dx
We know that sin2 x = (1 – cos2 x). we get
∫ (1 – cos2 x) (cos2 x) (sin x) dx
let cos x = t, =>t – sin x dx = dt.
Therefore,
∫ (1 – cos2 x) (cos2 x) (sin x) dx = – ∫ (1 – t2) t2 dt
= – ∫ (t2 – t4) dt
= – [(t3/3) – (t5/5)] + C
Hence, ∫ (sin3 x) (cos2 x) dx = – (1/3) cos3 x + (1/5) cos5 x + C
Integration using trigonometric identities:
- sin(α+β)=sin(α). cos(β)+cos(α). sin(β)
- sin(α–β)=sinα. cosβ–cosα. sinβ
- cos(α+β)=cosα. cosβ–sinα. sinβ
- cos(α–β)=cosα. cosβ+sinα. sinβ
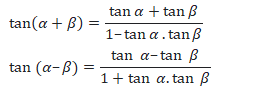
- sin 2θ = 2 sinθ cosθ
- cos 2θ = cos2θ – sin2 θ = 2 cos2θ – 1 = 1 – 2sin2 θ
- tan 2θ = (2tanθ)/(1 – tan2θ)
- sin (θ/2) = ±√[(1 – cosθ)/2]
- cos (θ/2) = ±√(1 + cosθ)/2
- tan (θ/2) = ±√[(1 – cosθ)(1 + cosθ)]
- Sin A. Sin B = [Cos (A – B) – Cos (A + B)]/2
- Sin A. Cos B = [Sin (A + B) – Sin (A – B)]/2
- Cos A. Cos B = [Cos (A + B) – Cos (A – B)]/2
- sin2 x + cos2 x = 1
1+tan2 x = sec2 x
cosec2 x = 1 + cot2 x - sin2 x =(1-cos2x)/2
- cos2 x =(1+cos2x)/2
tan2 x = sec2 x-1
cosec2 x - 1 = cot2 x - sin 3x = 3 sin x – 4 sin3 x,
- cos 3x = 4 cos3 x -3 cos x ,

Example :
Solve: ∫sin3x cos2x dx
Solution:
Given: ∫sin3x cos2x dx
∫sin3x cos2x dx = ∫sin2x sin x cos2x dx
We know that sin2x = 1-cos2x.
Therefore,
∫sin3x cos2x dx = ∫(1-cos2x)cos2x sinx dx
Now, let t = cos x, => dt = -sin x dx
Hence,
∫sin2x cos2x sin x dx = -∫(1-t2)t2 dt
= -∫(t2-t4) dt
∫sin2x cos2x sin x dx= -[(t3/3) -(t5/5)] + C
Now, let t = cos x, we get
∫sin2x cos2x sin x dx = -(⅓) cos3x + (⅕)cos5x + C
Therefore, ∫sin3x cos2x dx = -(⅓) cos3x + (⅕)cos5x + C.
Integrals of Some Particular Functions
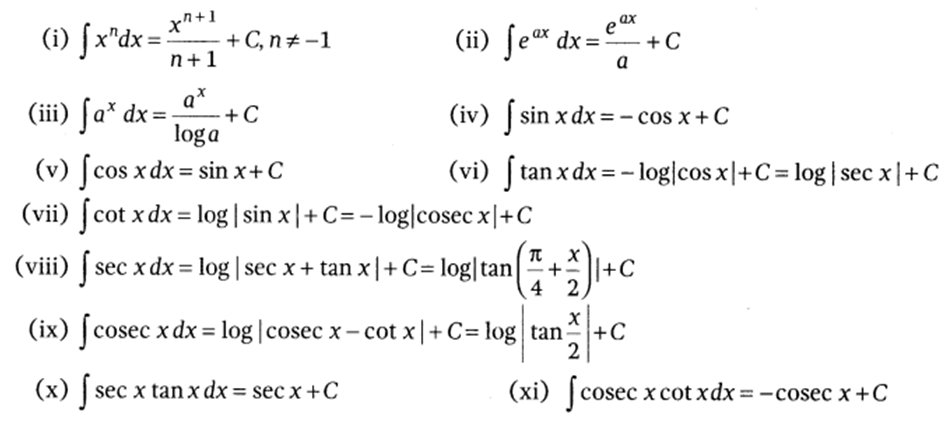
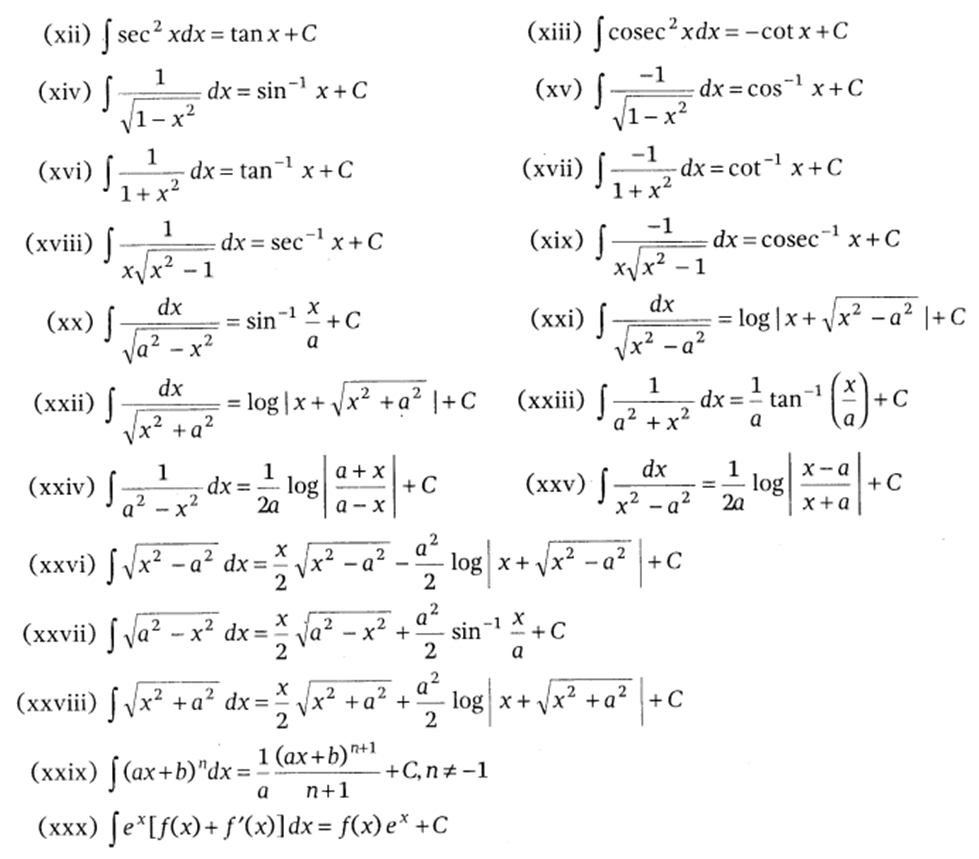
Integral of function
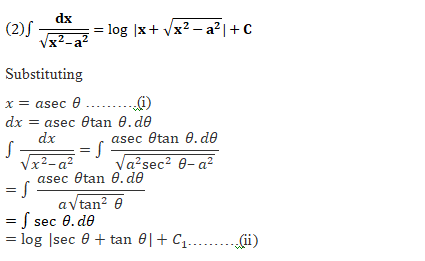
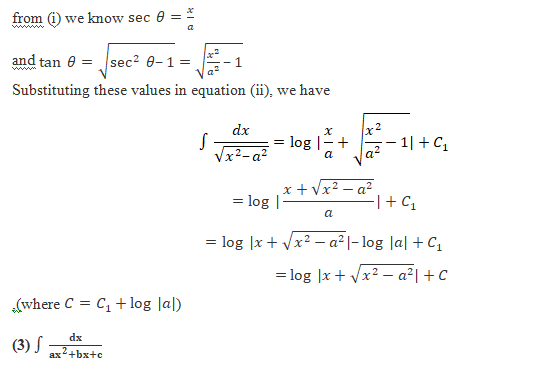
we equate the coefficient of x of both the sides to determine the value of A and B, and hence the integral is reduced to one of the known forms.
Example: Find the Integral of the function ![]()
Solution:The given function can be converted into the standard form
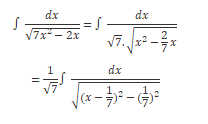

5. Methods of Integration(Integration by Partial Fractions)
- Books Name
- Mathmatics Book Based on NCERT
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 12
- Subject
- Mathmatics
Integration by Partial Fractions
If f(x) and g(x) are polynomial functions such function. that g(x) ≠ 0 then f(x)/g(x) is called Rational Functions. If degree f(x) < degree g(x) then f(x)/g(x) is called a proper rational function then apply partial fraction method. If degree f(x) < degree g(x) then f(x)/g(x) is called an improper rational function. If f(x)/g(x) is an improper rational function then by dividing f(x) by g(x), we can express f(x)/g(x) as the sum of a polynomial and a proper rational function, then apply partial fraction method.
Partial Fractions
Any proper rational function p(x)/q(x) can be expressed as the sum of rational functions, each having the simplest factor q(x), each such fraction is known as a partial function and the process of obtaining them is called the decomposition or resolving of the given function into partial fractions.

Example : Evaluate ʃ (x – 1)/(x + 1)(x – 2) dx
Solution:
Let (x – 1)/(x + 1)(x – 2) = A/(x + 1) + B/(x – 2)
Then, (x – 1) = A(x – 2) + B(x + 1) ………………(i)
Putting x = -1 in (i), we get A = 2/3
Putting x = 2 in (i), we get B = 1/3
Therefore,
(x – 1)/(x + 1)(x – 2) = 2/3(x + 1) + 1/3(x – 2)
=> ʃ (x – 1)/(x + 1)(x – 2) = 2/3ʃdx/(x + 1) + 1/3ʃdx/(x – 2)
= 2/3log | x + 1 | + 1/3 log | x – 2 | + C
Example : Evaluate ʃdx/(x3 + x2 + x + 1)
Solution:
We have 1/(x3 + x2 + x + 1) = 1/x2(x + 1) + (x + 1) = 1/(x + 1)(x2 + 1)
Let 1/(x + 1)(x2 + 1) = A/(x + 1) + Bx + C/(x2 + 1) ……………………(i)
=> 1 ≡ A(x2 + 1) + (Bx + C) (x + 1)
Putting x = -1 on both sides of (i), we get A = 1/2.
Comparing coefficients of x2 on the both sides of (i), we get
A + B = 0 => B = -A = -1/2
Comparing coefficients of x on the both sides of (i), we get
B + C = 0 => C = -B = 1/2
Therefore, 1/(x + 1) (x2 + 1) = 1/2(x + 1) + (-1/2x + 1/2)/(x2 + 1)
Therefore, ʃ1/(x + 1) (x2 + 1) = ʃdx/(x + 1) (x2 + 1)
= 1/2ʃdx/(x + 1) – 1/2ʃx/(x2 + 1)dx + 1/2ʃdx/(x2 + 1)
= 1/2ʃdx/(x + 1) – 1/4ʃ2x/(x2 + 1)dx + 1/2ʃdx/(x2 + 1)
= 1/2 log | x + 1 | – 1/4 log | x2 + 1 | + 1/2 tan-1x + C
Example : Evaluate ʃx2/(x2 + 2)(x2 + 3)dx
Solution:
Let x2/(x2 + 2) (x2 + 3) = y/(y + 2)(y + 3) where x2 = y.
Let y/(y + 2) (y + 3) = A/(y + 2) + B/(y + 3)
=> y ≡ A(y + 3) + B/(y + 2) ………………(i)
Putting y = -2 on the both sides of (i), we get A = -2.
Putting y = -3 on the both sides of (i), we get B = 3.
Therefore, y/(y + 2) (y + 3) = -2/(y + 2) + 3/(y + 3)
=> x2/(x2 + 2) (x2 + 3) = -2/(x2 + 2) + 3/(x2 + 3)
=> ʃx2/(x2 + 2) (x2 + 3) = -2ʃdx/(x2 + 2) + 3ʃdx/(x2 + 3)
= -2/√2tan-1(x/√2) + 3/√3tan-1(x/√3) + C
= -√2tan-1(x/√2) + √3tan-1(x/√3) + C
Example : Evaluate ʃdx/x(x4 + 1)?
Solution:
We have
I = ʃdx/x(x4 + 1) = ʃx3/x4 (x4 + 1) dx [multiplying numerator and denominator by x3].
Putting x4 = t and 4x3dx = dt, we get
I = 1/4ʃdt/t(t + 1)
= 1/4∫{1/t – 1/(t + 1)}dt [by partial fraction]
= 1/4ʃ1/t dt – 1/4ʃ1/(t + 1)dt
= 1/4 log | t | – 1/4 log | t + 1 | + C
= 1/4 log | x4 | – 1/4 log | x4 + 1 | + C
= (1/4 * 4) log | x | – 1/4 log | x4 + 1 | + C
= log | x | – 1/4 log | x4 + 1 | + C
6. Methods of Integration(Integration by Parts)
- Books Name
- Mathmatics Book Based on NCERT
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 12
- Subject
- Mathmatics
Integration by Parts
∫f(x) g(x) dx = f(x)∫g(x)dx – ∫[f'(x)∫g(x)dx]dx
This is the basic formula which is used to integrate products of two functions by parts.
If we consider f as the first function and g as the second function, then this formula may be pronounced as:
“The integral of the product of two functions = (first function) × (integral of the second function) – Integral of [(differential coefficient of the first function) × (integral of the second function)]”.
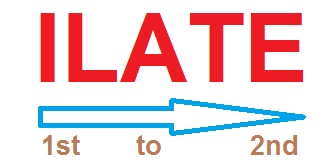
ILATE Rule
Identify the function that comes first on the following list and select it as f(x).
ILATE stands for:
I: Inverse trigonometric functions : tan-1 x, sec-1 x, sin-1 x etc.
L: Logarithmic functions : ln x, log5(x), etc.
A: Algebraic functions. such as,x ,x2 etc..
T: Trigonometric functions, such as sin x, cos x, tan x etc.
E: Exponential functions.
Example : Find ∫ x cos x dx
Solution: Let, The first function = f(x) = x and the second function = g(x) = cos x. Therefore, according to integration by parts, we have
∫ x cos x dx = x ∫ cos x dx – ∫ [(dx/dt) ∫ cos x dx] dx = x sin x – ∫ sin x dx
= x sin x + cos x + C.
Let’s try the other way round. Let, the first function = f(x) = cos x and the second function = g(x) = x. Therefore,
∫ x cos x dx = cos x ∫ x dx – ∫ {[d(cos x)/ dx] ∫ x } dx
= (cos x) (x2/2) + ∫ (sin x) (x2/2) dx
Example 2: Find ∫ log x dx
Solution: Do you know any function whose derivative is log x? Guessing it is difficult. Hence, let’s take the first function f(x) = log x. So, the second function g(x) = 1. And, we know that ∫ 1 dx = x. Therefore, ∫ g(x) dx = x. Therefore, we have,
Example: ![]()
Solution:


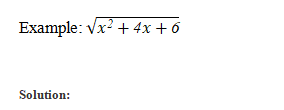

7. Integrals of some more types
- Books Name
- Mathmatics Book Based on NCERT
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 12
- Subject
- Mathmatics
Integrals of some more types
- ∫ √(x2 - a2) dx
- ∫ √(a2 - x2) dx
- ∫ √(x2 + a2) dx
Proof:
[1] ∫ √(x2 - a2) dx
Let I = ∫ √(x2 - a2) dx
⇒I = ∫ 1. √(x2 - a2) dx
⇒I = ∫ √(x2 - a2) . 1dx
Let f(x) = √(x2 - a2) and g(x) = 1
∫ f(x) g(x) dx = f(x) ∫ g(x) dx - ∫ [ f '(x) ∫ g(x) dx] dx
Thus ∫ √(x2 - a2) . 1dx = √(x2 - a2) . ∫ 1 dx - ∫ [d/dx(√(x2 - a2)) ∫1dx] dx
⇒ I = √(x2 - a2) . x - ∫ 1/(2(√(x2 - a2))) . 2x .x dx
⇒ I = x√(x2 - a2) - ∫ x2/√(x2 - a2) dx
⇒ I = x√(x2 - a2) - ∫ (x2 - a2 + a2)/√(x2 - a2) dx
⇒ I = x√(x2 - a2) - ∫ (x2 - a2)/√(x2 - a2) dx - ∫ a2/√(x2 - a2) dx
⇒ I = x√(x2 - a2) - ∫ √(x2 - a2) dx - ∫ a2/√(x2 - a2) dx
⇒ I = x √(x2 - a2) - I - ∫ a2/√(x2 - a2) dx
⇒ 2I = x √(x2 - a2) - a2 ∫ 1/√(x2 - a2) dx
⇒ 2I = x √(x2 - a2) - a2 log|x + √(x2 - a2)| + C
⇒ I = x/2 . √(x2 - a2) - a2/2 . log|x + √(x2 - a2)| + C
Note: The integral of √(x2 - a2) can also be evaluated by substituting x = a sec θ.
[2] ∫ √(x2 + a2) dx
Let I = ∫ √(x2 + a2) . 1dx
Let f(x) = √(x2 + a2) and g(x) =1
∫ f(x) g(x) dx = f(x) ∫ g(x) dx - ∫ [ f '(x) ∫ g(x) dx] dx
I = √(x2 + a2) ∫ 1 dx - ∫ [d/dx (√(x2 + a2)) ∫ 1dx] dx
⇒ I = √(x2 + a2) . x - ∫ 1/(2√(x2 + a2)). 2x . x dx
⇒ I = x √(x2 + a2) - ∫ x2/√(x2 + a2) dx
⇒ I = x √(x2 + a2) - ∫ (x2 + a2 - a2)/√(x2 + a2) dx
⇒ I = x√(x2 + a2) - ∫ (x2 - a2)/√(x2 + a2) dx + ∫ a2/√(x2 + a2) dx
⇒ I = x√(x2 + a2) - ∫ √(x2 + a2) dx + ∫ a2/√(x2 + a2) dx
⇒ I = x √(x2 + a2) - I + ∫ a2/√(x2 + a2) dx
⇒ 2I = x √(x2 + a2) + ∫ a2 /√(x2 + a2) dx
⇒ 2I = x √(x2 + a2) + a2 ∫ 1 /√(x2 + a2) dx
⇒ 2I = x √(x2 - a2) + a2 log|x + √(x2 + a2)| + C
⇒ I = x/2 . √(x2 + a2) + a2/2 . log|x + √(x2 + a2)| + C
Note: The integral of √(x2 + a2) can also be evaluated by substituting x = a tan θ.
[3] Let I= ∫ √(a2 - x2) dx
= ∫ √(a2 - x2) . 1 dx
= ∫ √(a2 - x2) . 1dx
Let f(x) = √(a2 - x2) and g(x) = 1
∫ f(x) g(x) dx = f(x) ∫ g(x) dx - ∫ [ f '(x) ∫ g(x) dx] dx
= √(a2 - x2) ∫ 1dx - ∫ [d/dx (√(a2 - x2)) ∫ 1dx] dx
⇒ I = √(a2 - x2) . x - ∫ 1/2(√(a2 - x2)) . (-2x) . x dx
⇒ I = x√(a2 - x2) - ∫ -x2/√(a2 - x2) dx
⇒ I = x√(a2 - x2) - ∫ ((a2-x2)-a2)/√(a2 - x2) dx
⇒ I = x√(a2 - x2) - ∫ (a2-x2)/√(a2 - x2) dx + ∫ a2/√(a2 - x2) dx
⇒ I = x√(a2 - x2) - ∫ √(a2 - x2) dx + ∫ a2/√(a2 - x2) dx
⇒ I = x√(a2 - x2) - I + ∫ a2/√(a2 - x2) dx
⇒ 2I = x√(a2 - x2) + a2 ∫ 1/√(a2 - x2) dx
⇒ 2I = x√(a2 - x2) + a2 sin-1 (x/a) + C
⇒ I = x/2 √(a2 - x2)+ a2/2 sin-1 (x/a) + C
Note: The integral of √(a2 - x2) can also be evaluated by substituting x = a sin θ.
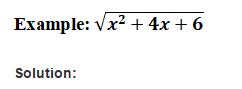

8. Concept of Definite Integral and Definite Integral as the limit of a sum
- Books Name
- Mathmatics Book Based on NCERT
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 12
- Subject
- Mathmatics
Definite Integral
A definite integral is denoted by ∫ab f(x) dx, where a is called the lower limit of the integral and b is called the upper limit of the integral.
Definite Integral as the limit of a sum:
The integral of f(x) is the area of the region bounded by the curve y = f(x). This area is represented by the region ABCD as shown in the above figure. This entire region lying between [a, b] is divided into n equal subintervals given by [x0, x1], [x1, x2], …… [xr-1, xr], [xn-1, xn].
Let us consider the width of each subinterval as h such that h → 0, x0 = a, x1 = a + h, x2 = a + 2h,…..,xr = a + rh, xn = b = a + nh
and n = (b – a)/h
Also, n→∞ in the above representation.
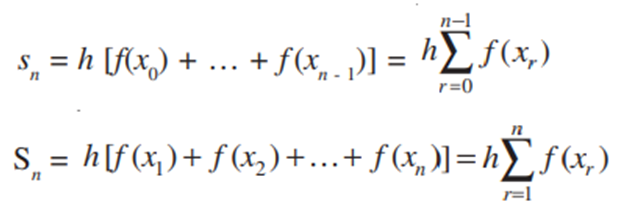
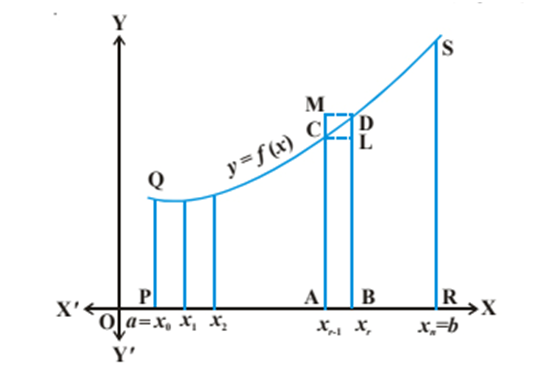
Since, n→∞, the rectangular strips are very narrow, it can be assumed that the limiting values of sn and Sn are equal and the common limiting value gives us the area under the curve, i.e.,

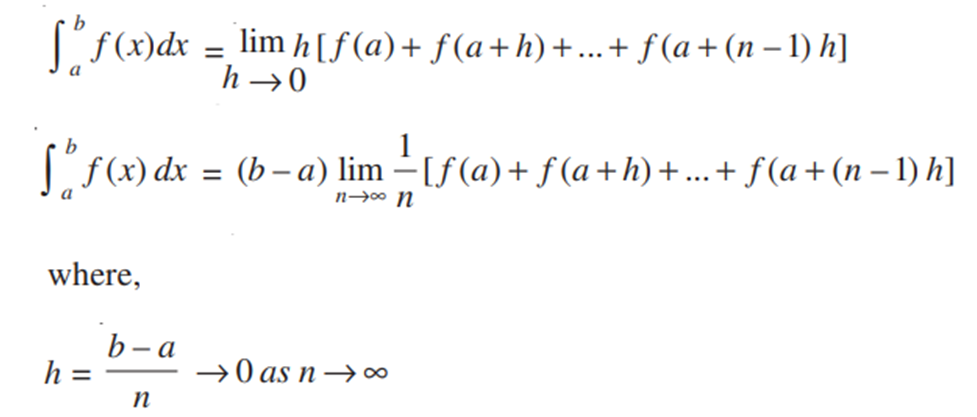
Question : Find ∫ab x dx as the limit of a sum.
Answer : From equation (6) above, we know that
∫ab f(x) dx = (b – a) limn → ∞ (1/n) [f(a) + f(a + h) + …. + f(a + {n – 1}h)]
Where, h = (b – a)/n
In this example, we have
a = a, b = b, f(x) = x and h = (b – a)/n.
Also, f(a) = a
f(a + h) = a + h
f(a + 2h) = a + 2h
f(a + 3h) = a + 3h ……
f(a + (n – 1)h) = a + (n – 1)h
Therefore,
∫ab x dx = (b – a) limn → ∞ (1/n) [f(a) + f(a + h) + f(a + 2h) + …. + f(a + {n – 1}h)]
= (b – a) limn → ∞ (1/n) [a + (a + h) + (a + 2h) + …. + (a + (n – 1)h)]
= (b – a) limn → ∞ (1/n) {[a + a + a + … + a(n-times)] + h + 2h + …. + (n – 1)h}
= (b – a) limn → ∞ (1/n) [na + h(1 + 2 + ….. + (n – 1)]
Now, we know that, 1 + 2 + 3 + … + n = n(n + 1)/2. Hence,
1 + 2 + 3 + … + (n – 1) = (n – 1)(n – 1 + 1)/2 = n(n – 1)/2
Therefore,
∫ab x dx = (b – a) limn → ∞ (1/n) [na + hn(n – 1)/2]
= (b – a) limn → ∞ [na/n + hn(n – 1)/2n]
= (b – a) limn → ∞ [a + (n – 1)h/2]
Replacing h by (b – a)/n, we get
∫ab x dx = (b – a) limn → ∞ [a + (n – 1) (b – a) / 2n]
= (b – a) limn → ∞ [a + (n/n – 1/n) {(b – a)/2}]
= (b – a) limn → ∞ [a + (1 – 1/n){(b – a)/2}]
= (b – a) [a + (1 – 1/∞) {(b – a)/2}]
= (b – a) [a + (1 – 0){(b – a)/2}]
= (b – a) [a + (b – a)/2]
= (b – a) (2a + b – a)/2
= (b – a) (b + a)/2
= (b2 – a2)/2
Hence, the definite integral ∫ab x dx as the limit of sum is [(b2 – a2)/2].
Example: Find ∫02 (x2 + 1) dx as the limit of a sum.
Solution: From above, we know that
∫ab f(x) dx = (b – a) limn → ∞ (1/n) [f(a) + f(a + h) + …. + f(a + {n – 1}h)]
Where, h = (b – a)/n
we have a = 0, b = 2, f(x) = (x2 + 1) and h = (2 – 0)/n = 2/n. Therefore,
∫02 (x2 + 1) dx = 2 limn → ∞ (1/n) [f(0) + f(2/n) + f(4/n) + …. + f(2{n – 1}/n)]
= 2 limn → ∞ (1/n) [1 + {(22/n2) + 1} + {(42/n2) + 1} + …. + {(2n – 2)2/n2 + 1}]
= 2 limn → ∞ (1/n) [1 + 1 + 1 + … + 1(n-times)] + 1/n2) [22 + 42 + … (2n – 2)2]
= 2 limn → ∞ (1/n) [n + 22/n2 (12 + 22 + … (n – 1)2]
= 2 limn → ∞ (1/n) [n + 4/n2 {(n – 1) n (2n – 1) / 6}]
= 2 limn → ∞ (1/n) [n + 2/3 {(n – 1) (2n – 1) / n}]
= 2 limn → ∞ (1/n) [n + 2/3 (1 – 1/n) (2 – 1/n)]
As n → ∞, 1/n → 0. Therefore, we have
∫02 (x2 + 1) dx = 2 [1 + 4/3] = 14/3.
9. Fundamental Theorem of Calculus
- Books Name
- Mathmatics Book Based on NCERT
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 12
- Subject
- Mathmatics
Fundamental Theorem of Calculus
Fundamental theorem of calculus contains two important theorems namely:
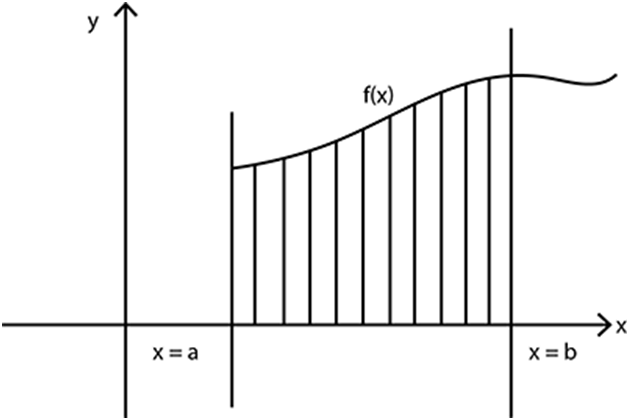
First fundamental theorem of integral calculus
Let f be a continuous function on the closed interval [a, b] and let A (x) be the area function. Then A′(x) = f (x), for all x ∈ [a, b].
Second fundamental theorem of integral calculus
Let f be a continuous function defined on the closed interval [a, b] and F be an antiderivative of f.
Then ∫ab f(x) dx= [F(x)]ab = F(b) – F(a)
10. Evaluation of Definite Integrals by Substitution and more methods
- Books Name
- Mathmatics Book Based on NCERT
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 12
- Subject
- Mathmatics
Evaluation of Definite Integrals by Substitution and more methods:
To evaluate ![]() by substitution, the steps could be as follows:
by substitution, the steps could be as follows:
1. Consider the integral without limits and substitute, y = f (x) or x = g(y) to reduce
the given integral to a known form.
2. Integrate the new integrand with respect to the new variable without mentioning
the constant of integration.
3. Re-substitute for the new variable and write the answer in terms of the original
variable.
4. Find the values of answers obtained in (3) at the given limits of integral and find
the difference of the values at the upper and lower limits. Although we will not formally prove this theorem, we justify it with some calculations here. From the substitution rule for indefinite integrals, if F(x) is an anti-derivative of f(x) we have
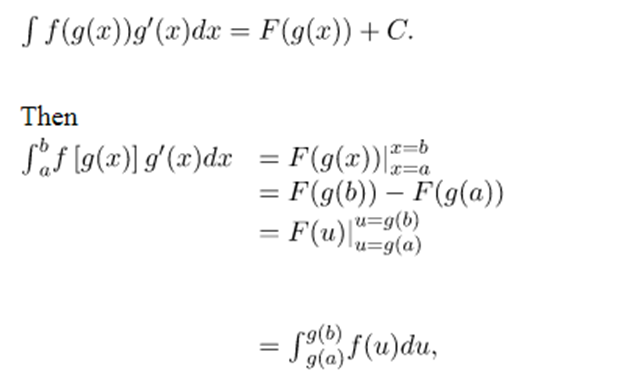
and we have the desired result.Using substitution to evaluate a definite integral requires a change to the limits of integration. If we change variables in the integrand, the limits of integration change as well.


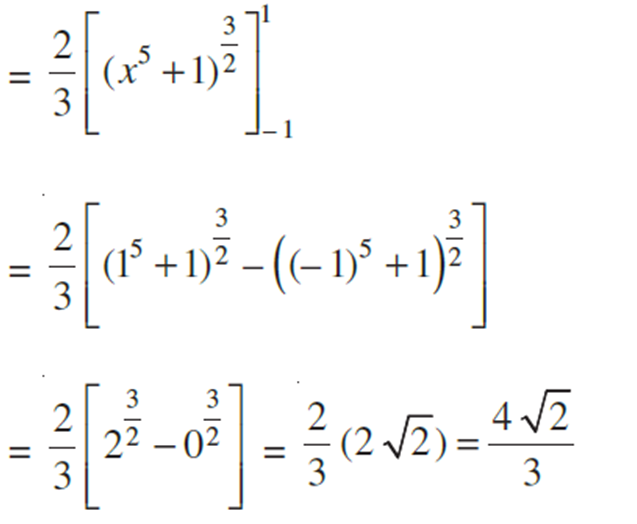
Alternatively, first we transform the integral and then evaluate the transformed integral with new limits.
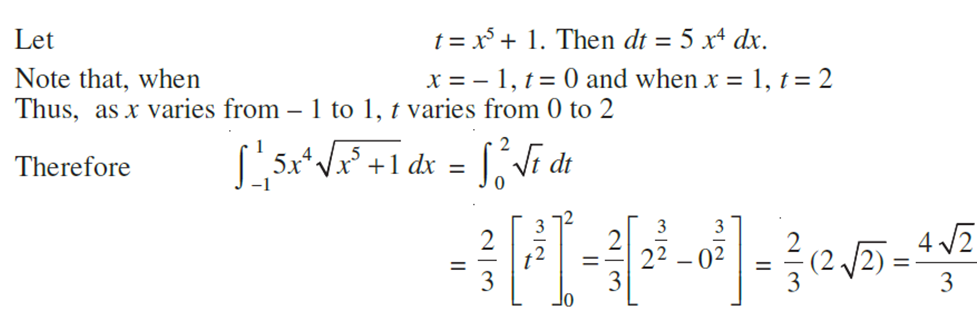
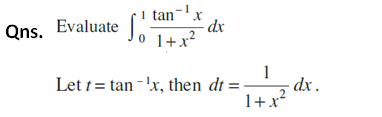
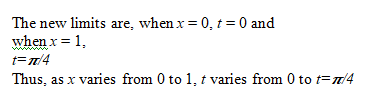
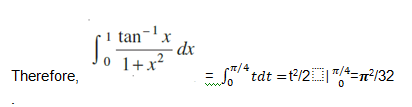
11. Some Properties of Definite Integrals and evaluation of definite integrals
- Books Name
- Mathmatics Book Based on NCERT
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 12
- Subject
- Mathmatics
Some Properties of Definite Integrals and evaluation of definite integrals


Example :
Prove that 0∫π/2 (2log sinx – log sin 2x)dx = – (π/2) log 2
Solution:
To prove: 0∫π/2 (2log sinx – log sin 2x)dx = – (π/2) log 2
Proof:
Let I = 0∫π/2 (2log sinx – log sin 2x)dx ………………………….…(1)
By using the property of definite integral
0∫a f(x) dx = 0∫a f(a-x) dx
Now, apply the property in (1), we get
-
- I = 0∫π/2 2log sin[(π/2)-x] – log sin 2[(π/2)-x])dx
The above expression can be written as
-
- I = 0∫π/2 [2log cosx- log sin(π-2x)]dx (Since, sin (90-θ = cos θ)
- I = 0∫π/2 [2log cosx- log sin2x]dx ……………………………………………………..(2)
Now, add the equation (1) and (2), we get
-
- I+ I = 0∫π/2 [(2log sinx – log sin 2x) +(2log cosx- log sin2x)]dx
- 2I = 0∫π/2 [2log sinx -2log 2sinx + 2log cos x]dx
- 2I = 2 0∫π/2 [log sinx -log 2sinx + log cos x]dx
-
- = 0∫π/2 [log sinx + log cos x- log 2sinx]dx
-
- I = 0∫π/2log[(sinx. cos x)/sin2x]dx
We know that sin2x= 2 sinx cos x)
-
- I = 0∫π/2log[(sinx. cos x)/(2 sinx cos x)]dx
- I = 0∫π/2 log(1/2)dx
- I = 0∫π/2 (log1-log 2)dx [Since, log (a/b) = log a- log b]
- I = 0∫π/2 -log 2 dx (value of log 1 = 0)
Now, take the constant – log 2 outside the integral,
-
- I = -log 2 0∫π/2dx
Now, integrate the function
-
- I = -log 2 [x]0π/2
Now, substitute the limits
-
- I = -log 2 [(π/2)-0]
- I = – log 2 (π/2)
- I = – (π/2) log 2 = R.H.S
Therefore, L.H. S = R.H.S
Hence. 0∫π/2 (2log sinx – log sin 2x)dx = – (π/2) log 2 is proved.
Example: solve ![]()
Solution:

Question. 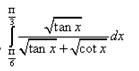
Solution:
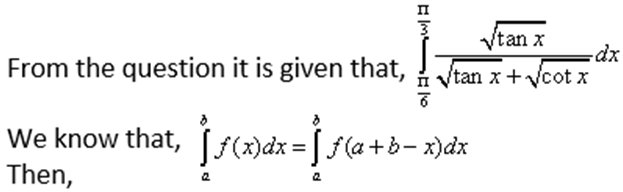

Now applying limits, we get,
2I = π/3 – π/6
2I = (2π – π)/6
2I = π/6
I = π/12
Question. 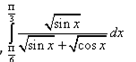
Solution:

Now applying limits, we get,
2I = π/3 – π/6
2I = (2π – π)/6
2I = π/6
I = π/12
Question. 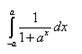
Solution:

Question. 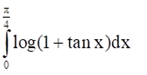
Solution:

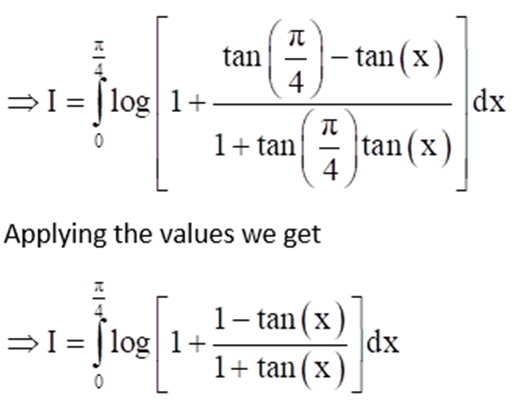


 KRISHNA PUBLICATIONS
KRISHNA PUBLICATIONS

