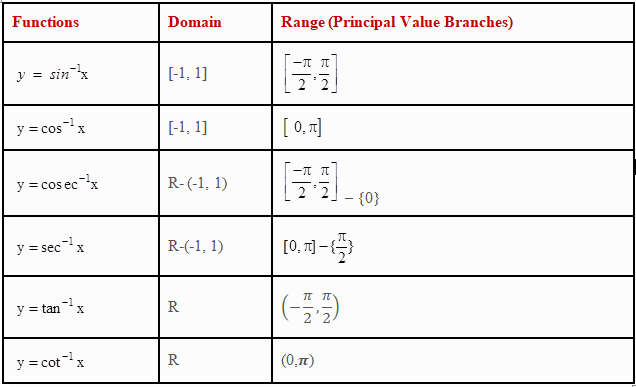
1. Basic concepts , Domain and Range ,Principal Branch
- Books Name
- Mathmatics Book Based on NCERT
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 12
- Subject
- Mathmatics
Chapter-2
Inverse Trigonometric functions
Basic concepts , Domain and Range ,Principal Branch:
Let y = sinx => x = sin-1y
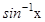 should not be confused with
should not be confused with 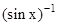 . In fact
. In fact 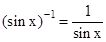
- i.e.,
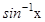 ¹
¹ 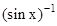
- And similarly for other trigonometric functions.
- The value of an inverse trigonometric functions which lies in its principal value branch is called the principal value of that inverse trigonometric functions.
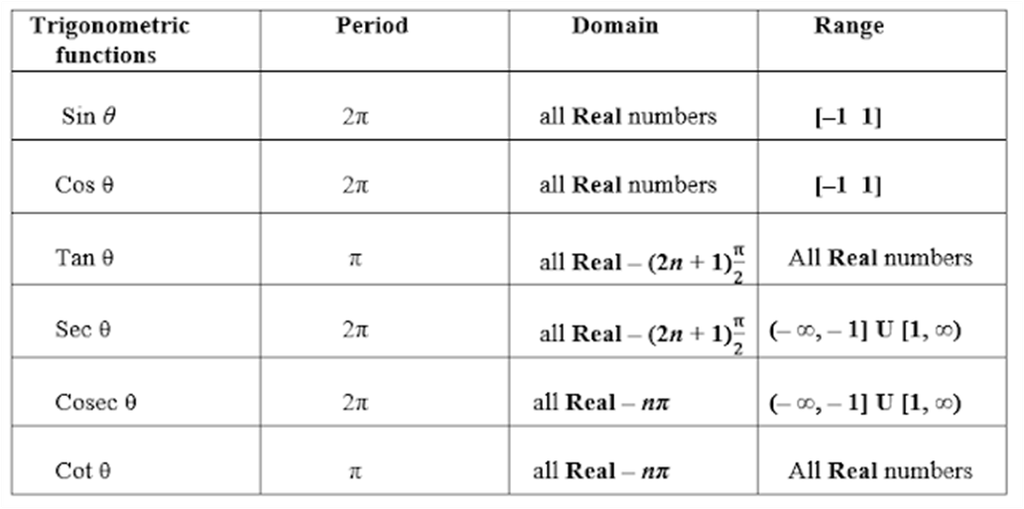
- The domains and ranges (principal value branches) of inverse trigonometric functions are given in the following table:
- The functions
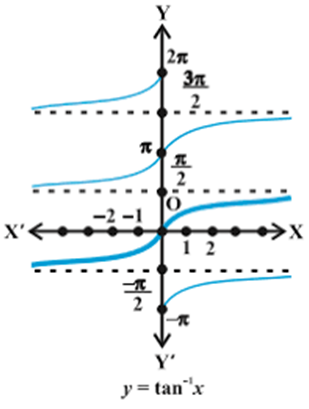
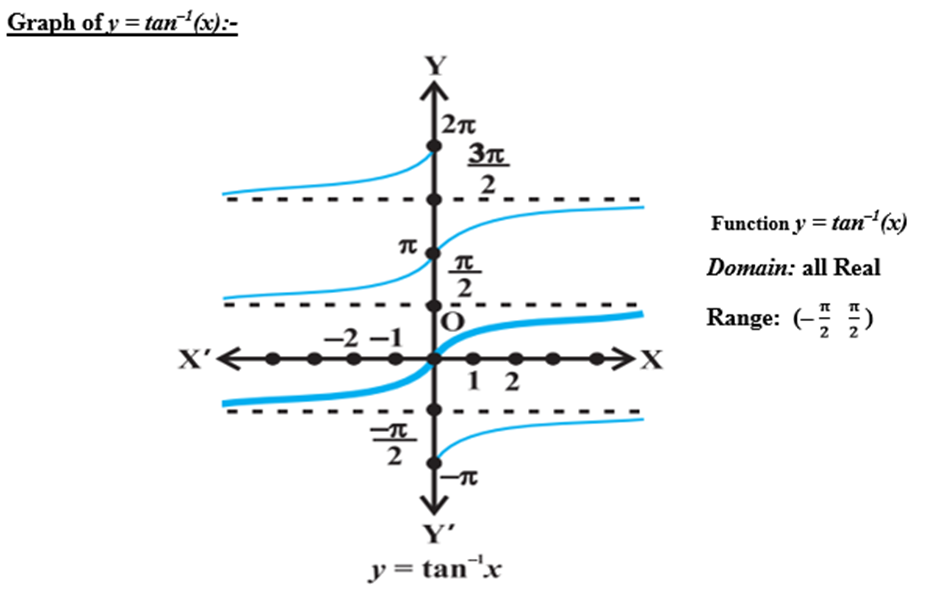
sin−1x & tan−1x
are increasing functions in their domain.
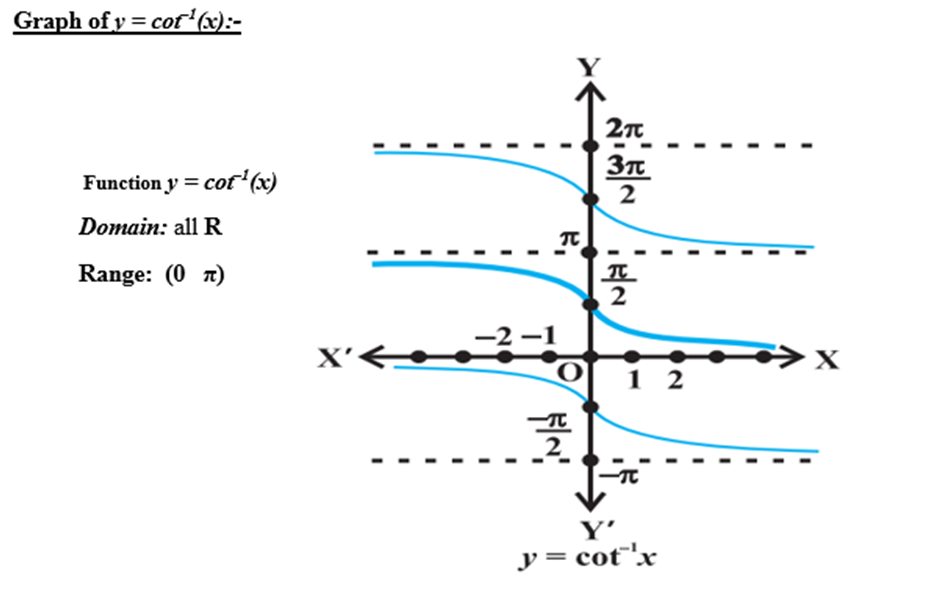
- The functions
cos−1x & cot−1x
are decreasing functions in over domain.
For suitable values of domain, we have
• ![]()
• ![]()
2. Graphs of inverse trigonometric functions
- Books Name
- Mathmatics Book Based on NCERT
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 12
- Subject
- Mathmatics
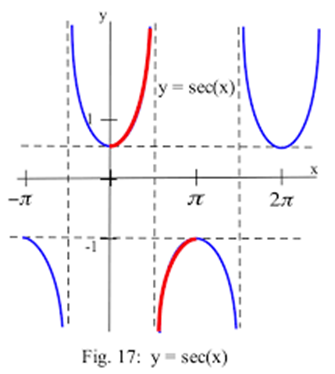
Graphs of inverse trigonometric functions
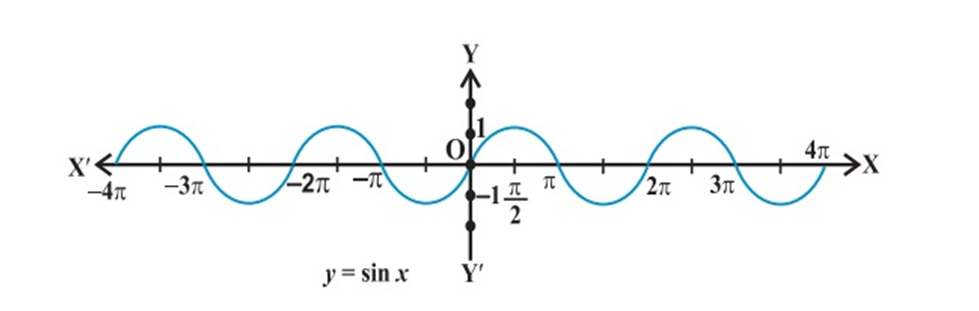
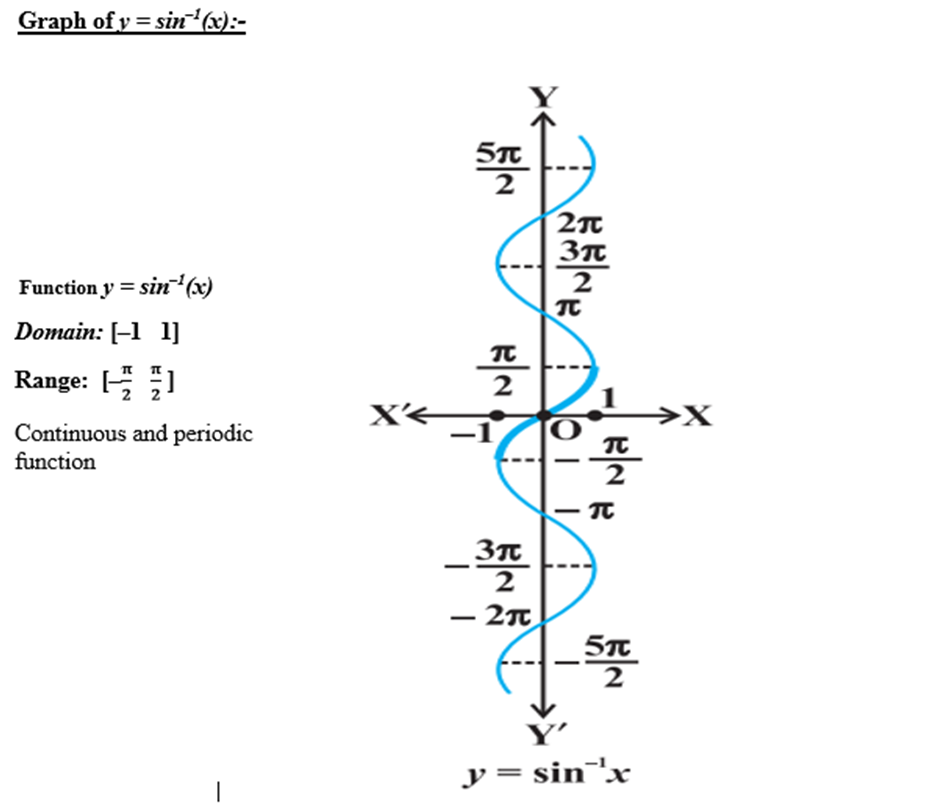
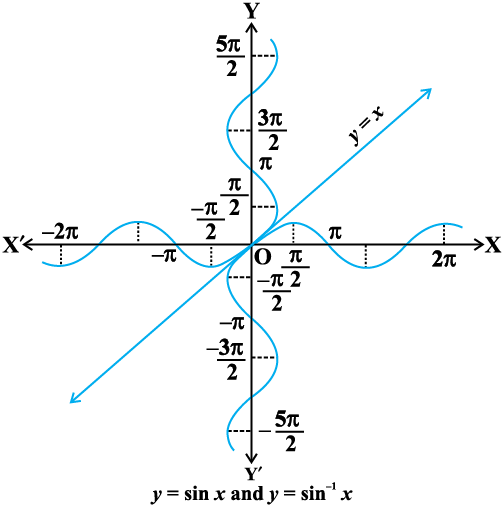
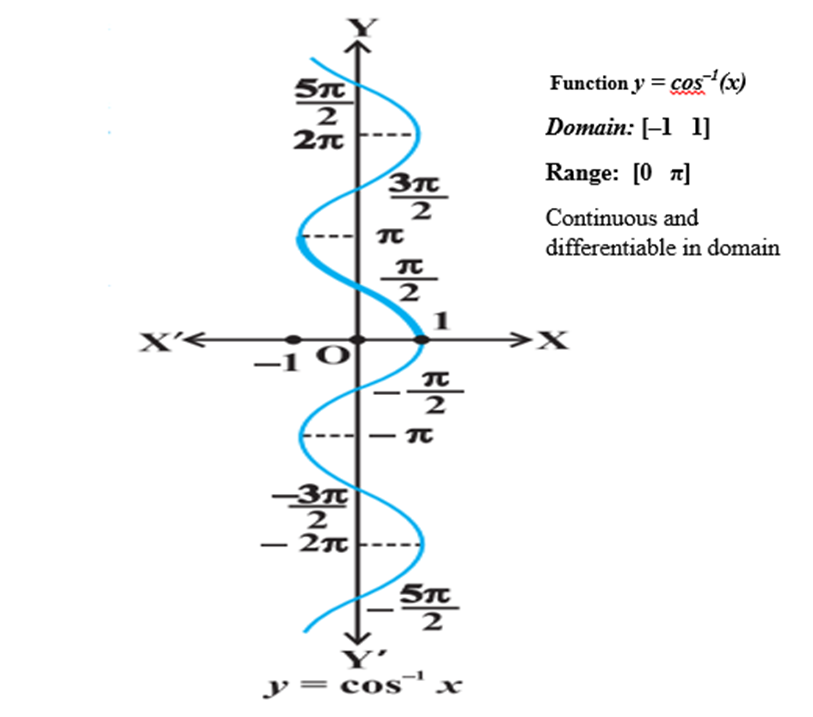
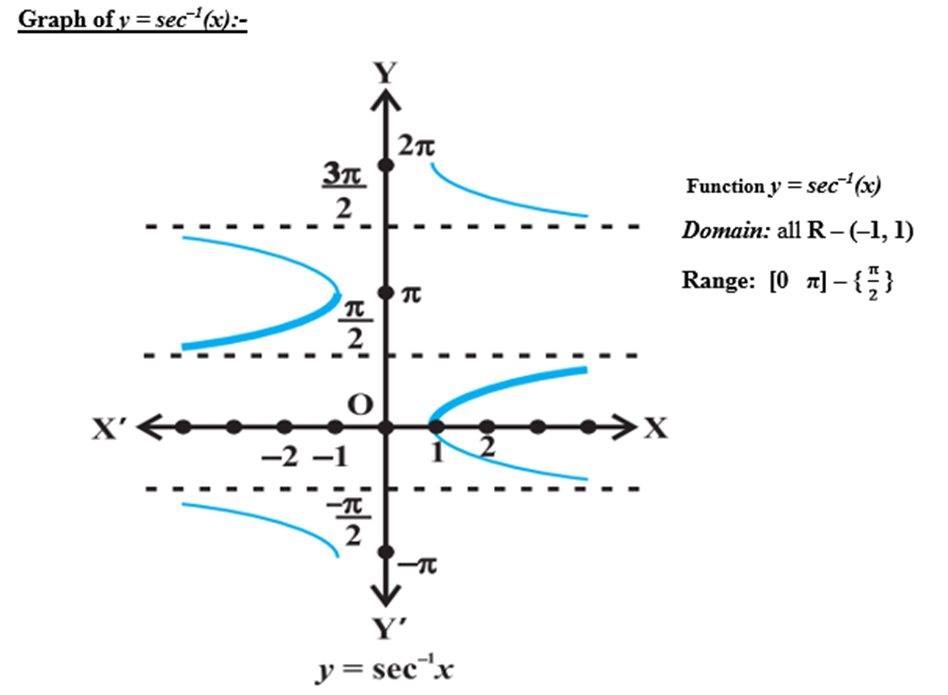
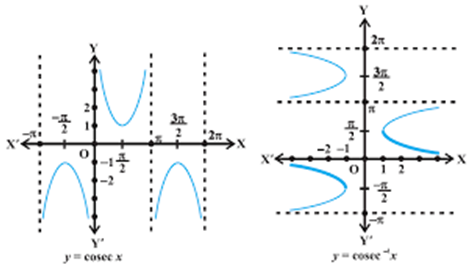
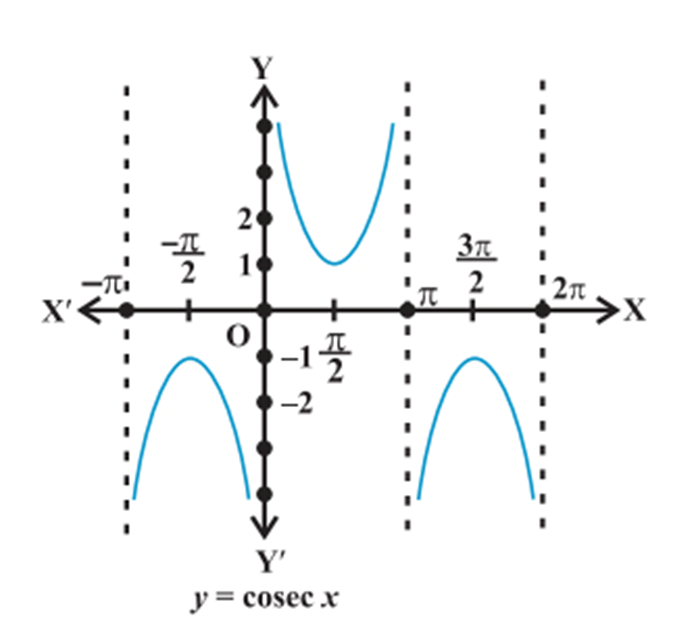
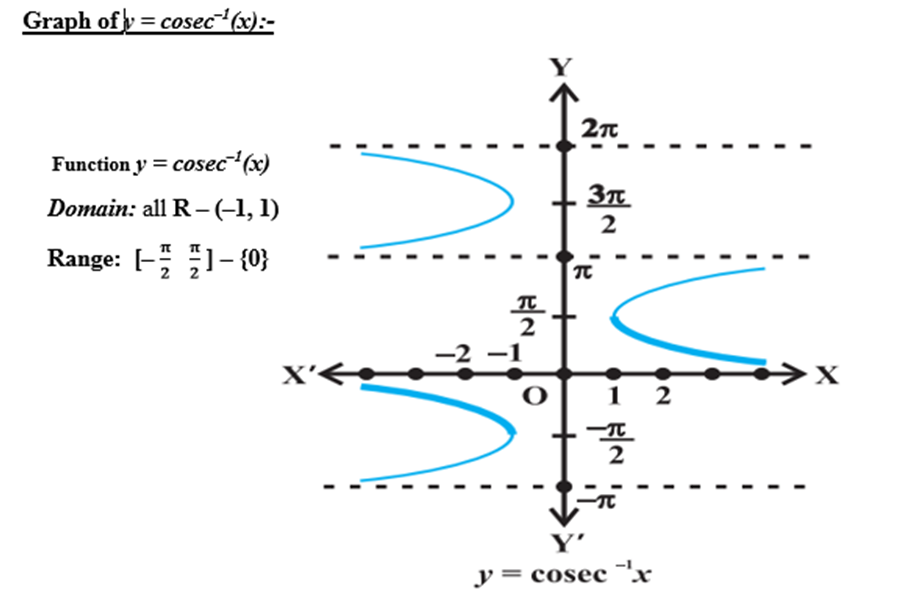
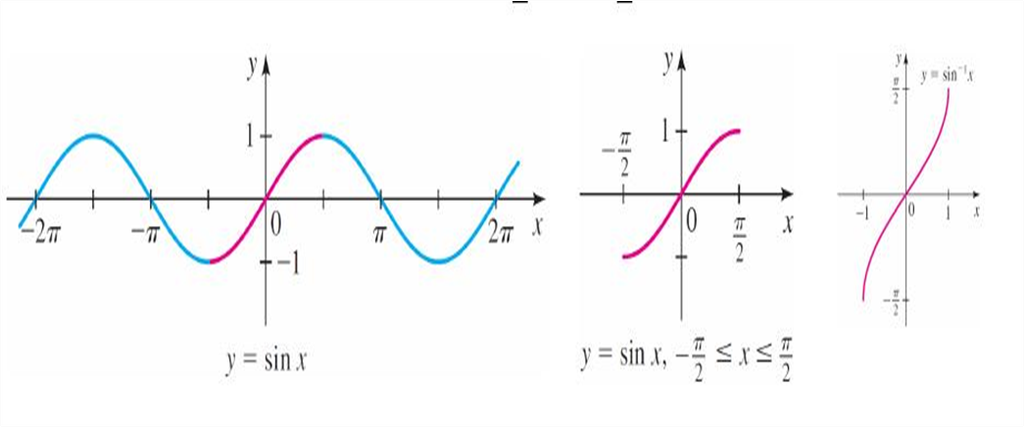

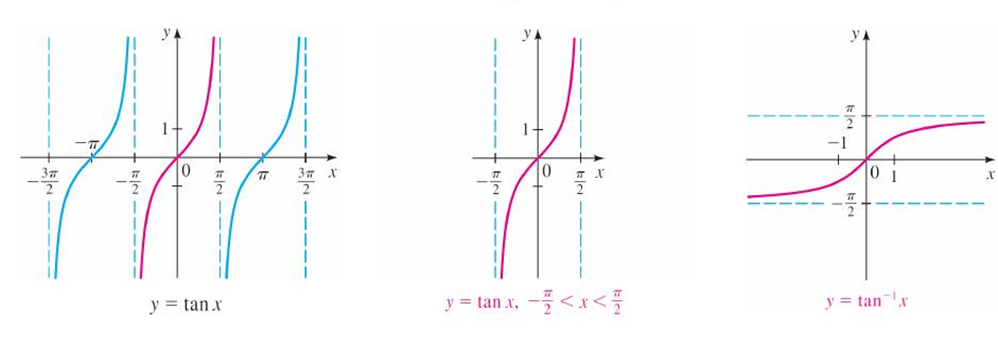
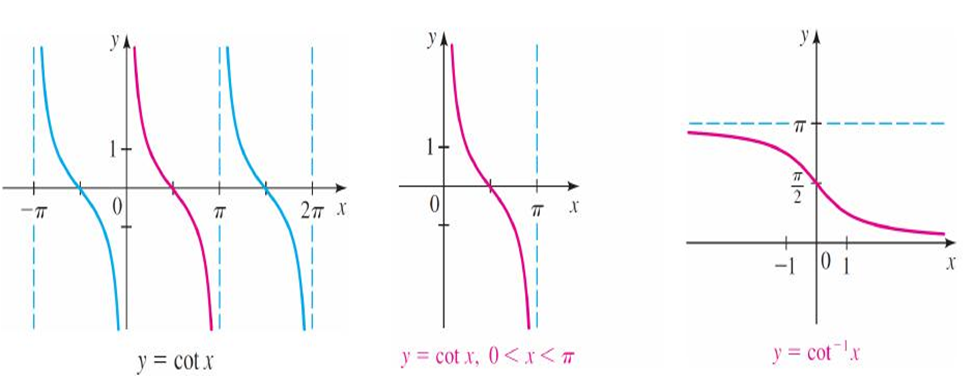
3. Properties of inverse trigonometric functions and important results
- Books Name
- Mathmatics Book Based on NCERT
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 12
- Subject
- Mathmatics
Properties of inverse trigonometric functions and important results
Properties:
[1]
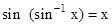
- cos(cos-1x)=x
- tan(tan-1x)=x
- cot(cot-1x)=x
- cosec(cosec-1x)=x
- sec(sec-1x)=x
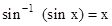
- Cos-1(cosx)=x
- tan-1(tanx)=x
- cot-1 (cotx)=x
- cosec-1 (cosecx)=x
- sec-1 (secx)=x
[2]
[3]
- sin–1 (–x) = – sin–1 x
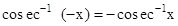
- tan–1 (–x) = – tan–1 x
[4]
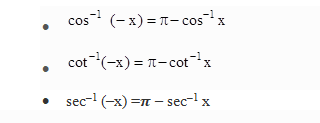
[5]
- tan–1 x + cot–1 x = π/2
- sin–1 x + cos–1 x = π/2
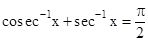
[6]
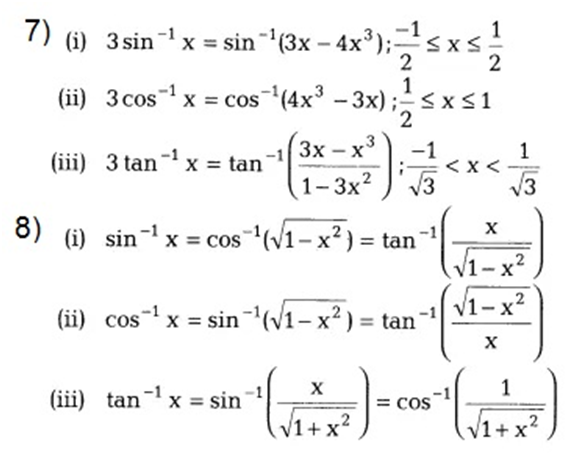
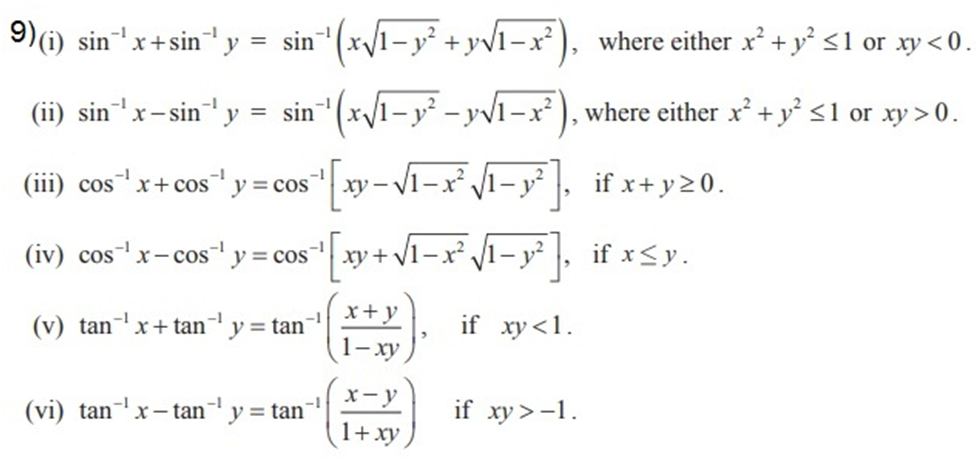
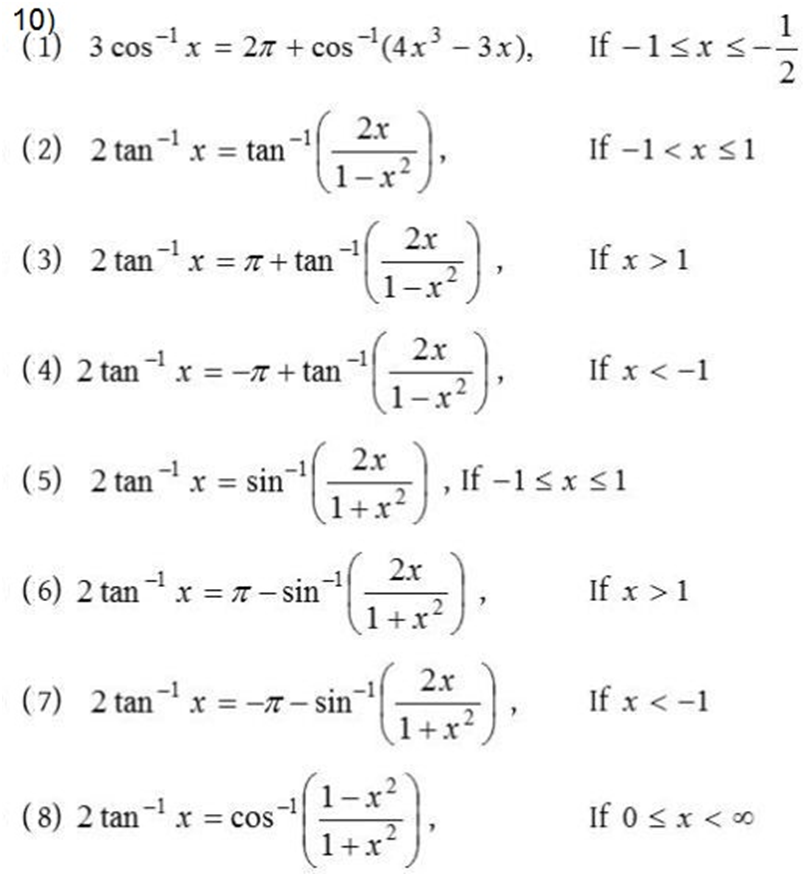
Examples:
1. Find the domain of definition of f(x) = cos -1 (x2 – 4)
Solution:
Given f(x) = cos -1 (x2 – 4)
We know that domain of cos-1 (x2 – 4) lies in the interval [-1, 1]
Therefore, we can write as
-1 ≤ x2 – 4 ≤ 1
4 – 1 ≤ x2 ≤ 1 + 4
3 ≤ x2 ≤ 5
±√ 3 ≤ x ≤ ±√5
– √5 ≤ x ≤ – √3 and √3 ≤ x ≤ √5
Therefore domain of cos-1 (x2 – 4) is [- √5, – √3] ∪ [√3, √5]
2. Find the domain of f(x) = cos-1 2x + sin-1 x.
Solution:
Given that f(x) = cos-1 2x + sin-1 x.
Now we have to find the domain of f(x),
We know that domain of cos-1 x lies in the interval [-1, 1]
Also know that domain of sin-1 x lies in the interval [-1, 1]
Therefore, the domain of cos-1 (2x) lies in the interval [-1, 1]
Hence we can write as,
-1 ≤ 2x ≤ 1
– ½ ≤ x ≤ ½
Hence, domain of cos-1(2x) + sin-1 x lies in the interval [- ½, ½]
3. Find the principal value of each of the following:
(i) sec-1 (-√2)
(ii) sec-1 (2)
(iii) sec-1 (2 sin (3π/4))
(iv) sec-1 (2 tan (3π/4))
Solution:
(i) Given sec-1 (-√2)
Now let y = sec-1 (-√2)
Sec y = -√2
We know that sec π/4 = √2
Therefore, -sec (π/4) = -√2
= sec (π – π/4)
= sec (3π/4)
Thus the range of principal value of sec-1 is [0, π] – {π/2}
And sec (3π/4) = – √2
Hence the principal value of sec-1 (-√2) is 3π/4
(ii) Given sec-1 (2)
Let y = sec-1 (2)
Sec y = 2
= Sec π/3
Therefore the range of principal value of sec-1 is [0, π] – {π/2} and sec π/3 = 2
Thus the principal value of sec-1 (2) is π/3
(iii) Given sec-1 (2 sin (3π/4))
But we know that sin (3π/4) = 1/√2
Therefore 2 sin (3π/4) = 2 × 1/√2
2 sin (3π/4) = √2
Therefore by substituting above values in sec-1 (2 sin (3π/4)), we get
Sec-1 (√2)
Let Sec-1 (√2) = y
Sec y = √2
Sec (π/4) = √2
Therefore range of principal value of sec-1 is [0, π] – {π/2} and sec (π/4) = √2
Thus the principal value of sec-1 (2 sin (3π/4)) is π/4.
(iv) Given sec-1 (2 tan (3π/4))
But we know that tan (3π/4) = -1
Therefore, 2 tan (3π/4) = 2 × -1
2 tan (3π/4) = -2
By substituting these values in sec-1 (2 tan (3π/4)), we get
Sec-1 (-2)
Now let y = Sec-1 (-2)
Sec y = – 2
– sec (π/3) = -2
= sec (π – π/3)
= sec (2π/3)
Therefore the range of principal value of sec-1 is [0, π] – {π/2} and sec (2π/3) = -2
Thus, the principal value of sec-1 (2 tan (3π/4)) is (2π/3).
4. Evaluate:
(i) Cot (sin-1 (3/4) + sec-1 (4/3))
(ii) Sin (tan-1 x + tan-1 1/x) for x < 0
Solution:
(i) Given Cot (sin-1 (3/4) + sec-1 (4/3))
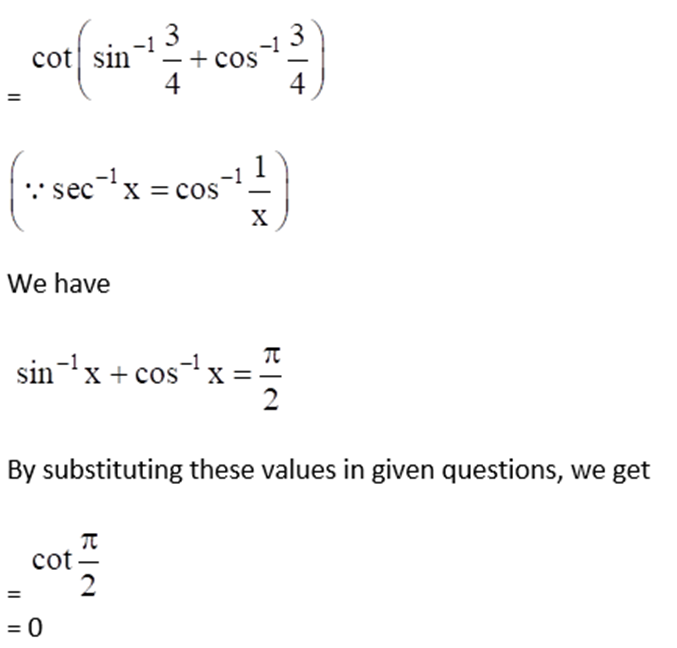
(ii) Given Sin (tan-1 x + tan-1 1/x) for x < 0
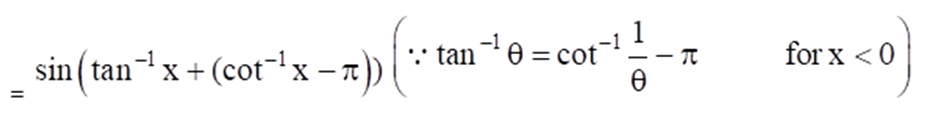
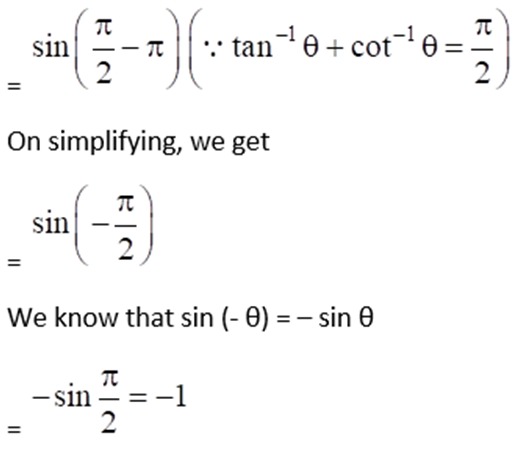
5. If cos-1 (x/2) + cos-1 (y/3) = α, then prove that 9x2 – 12xy cos α + 4y2 = 36 sin2 α
Solution:
Given cos-1 (x/2) + cos-1 (y/3) = α
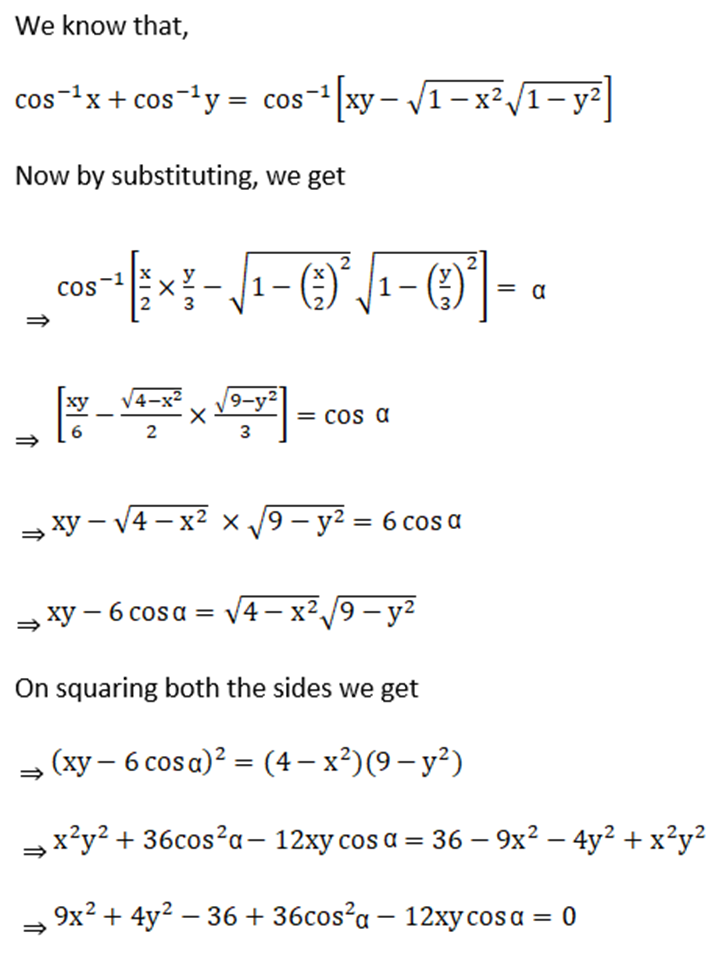
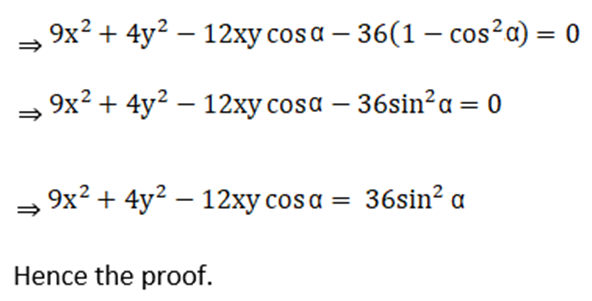
6. If sin-1 (2a/1 + a2) – cos-1(1 – b2/1 + b2) = tan-1(2x/1 – x2), then prove that x = (a – b)/ (1 + a b)
Solution:
Given sin-1 (2a/1 + a2) – cos-1(1 – b2/1 + b2) = tan-1(2x/1 – x2)

7. If sin-1 x + sin-1 y = π/3 and cos-1 x – cos-1 y = π/6, find the values of x and y.
Solution:
Given sin-1 x + sin-1 y = π/3 ……. Equation (i)
And cos-1 x – cos-1 y = π/6 ……… Equation (ii)
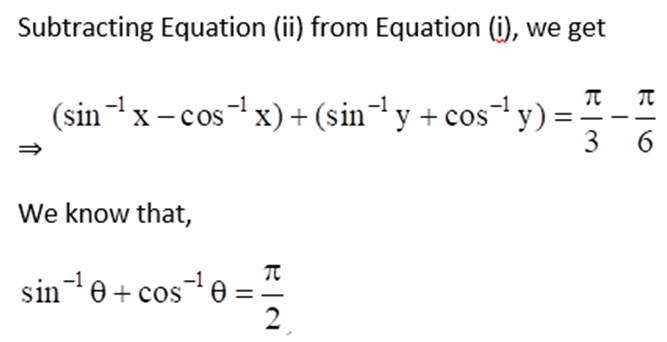
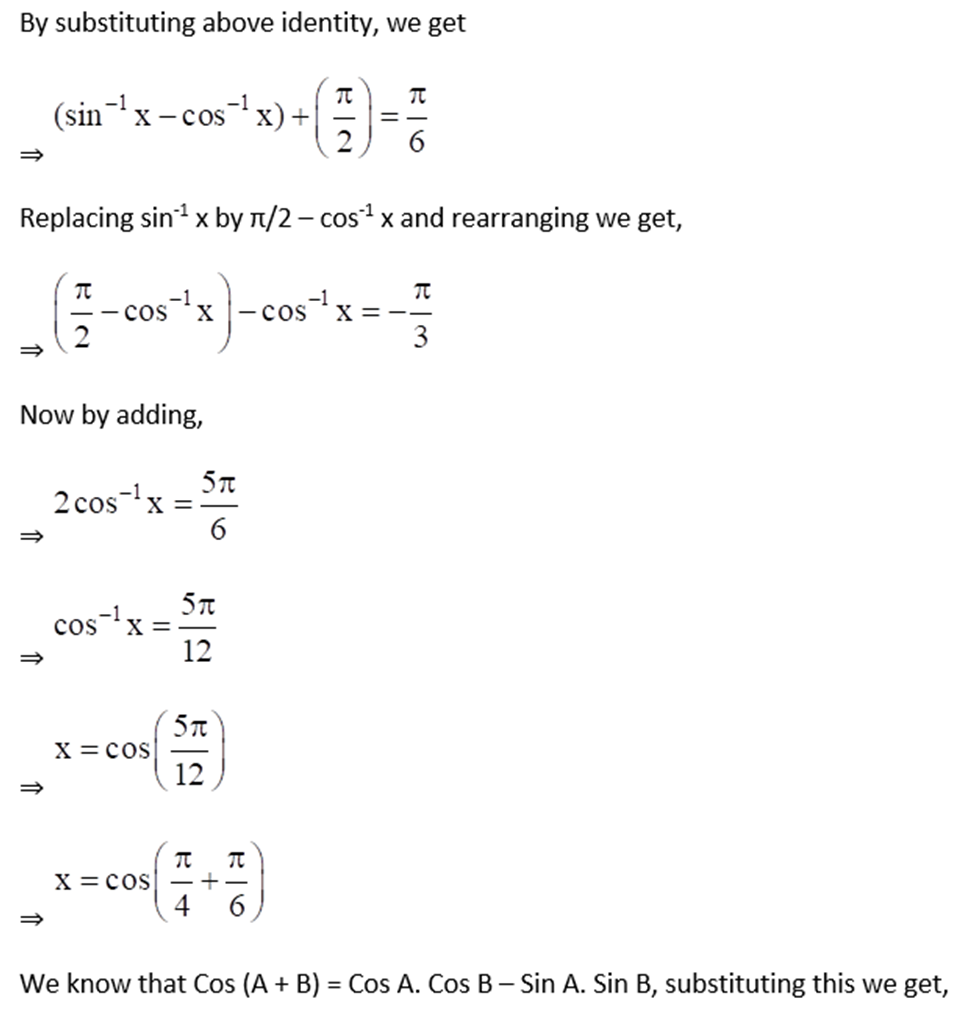
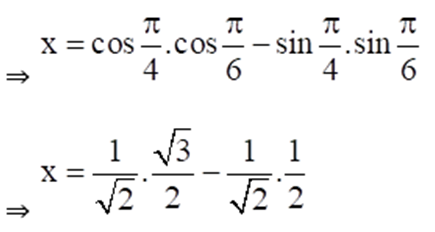
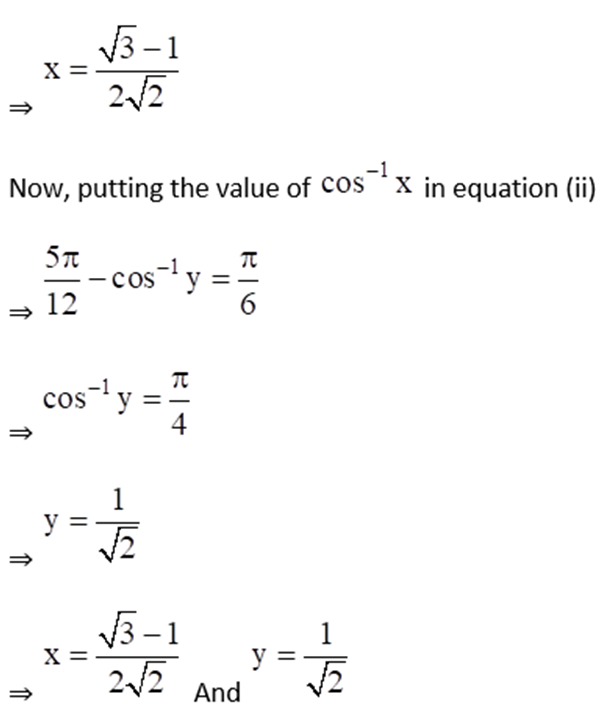

8. Which of the following is the principal value branch of cos-1 x?
(a) [-π/2, π/2] (b) (0, π) (c) [0. π] (d) [0, π] – {π/2}
Solution:
(c) [0. π]
As we know that the principal value branch cos-1 x is [0, π].
9. Which of the following is the principal value branch of cosec-1 x?
(a) (-π/2, π/2) (b) [0, π] – {π/2} (c) [-π/2, π/2] (d) [-π/2, π/2] – {0}
Solution:
(d) [-π/2, π/2] – {0}
As the principal branch of cosec-1 x is [-π/2, π/2] – {0}.
10. If 3 tan-1 x + cot-1 x = π, then x equals
(a) 0 (b) 1 (c) -1 (d) ½
Solution:
(b) 1
Given, 3 tan-1 x + cot-1 x = π
2 tan-1 x + tan-1 x + cot-1 x = π
2 tan-1 x + π/2 = π (As tan-1 + cot-1 = π/2)
2 tan-1 x = π/2
tan-1 x = π/4
x = 1
11. The value of sin-1 cos 33π/5 is
(a) 3π/5 (b) -7π/5 (c) π/10 (d) -π/10
Solution:
(d) -π/10

 Chintu
Chintu
