- Books Name
- Mathmatics Book Based on NCERT
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 12
- Subject
- Mathmatics
Some Properties of Definite Integrals and evaluation of definite integrals


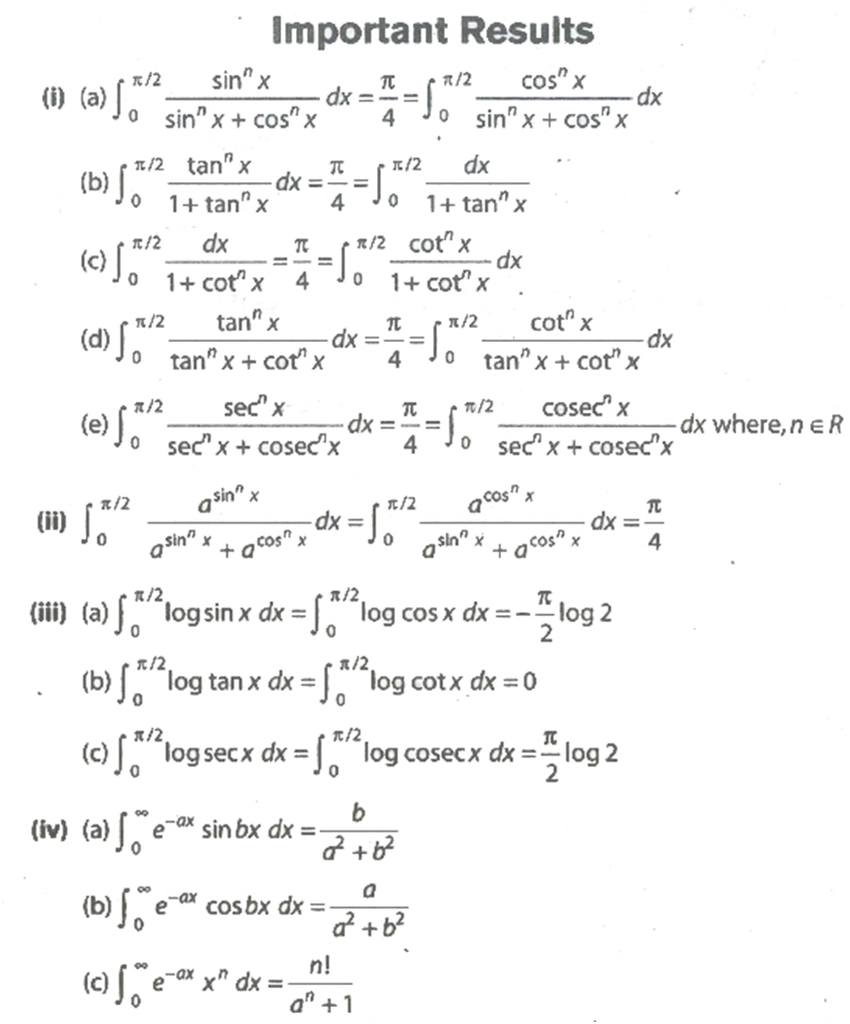
Example :
Prove that 0∫π/2 (2log sinx – log sin 2x)dx = – (π/2) log 2
Solution:
To prove: 0∫π/2 (2log sinx – log sin 2x)dx = – (π/2) log 2
Proof:
Let I = 0∫π/2 (2log sinx – log sin 2x)dx ………………………….…(1)
By using the property of definite integral
0∫a f(x) dx = 0∫a f(a-x) dx
Now, apply the property in (1), we get
-
- I = 0∫π/2 2log sin[(π/2)-x] – log sin 2[(π/2)-x])dx
The above expression can be written as
-
- I = 0∫π/2 [2log cosx- log sin(π-2x)]dx (Since, sin (90-θ = cos θ)
- I = 0∫π/2 [2log cosx- log sin2x]dx ……………………………………………………..(2)
Now, add the equation (1) and (2), we get
-
- I+ I = 0∫π/2 [(2log sinx – log sin 2x) +(2log cosx- log sin2x)]dx
- 2I = 0∫π/2 [2log sinx -2log 2sinx + 2log cos x]dx
- 2I = 2 0∫π/2 [log sinx -log 2sinx + log cos x]dx
-
- = 0∫π/2 [log sinx + log cos x- log 2sinx]dx
-
- I = 0∫π/2log[(sinx. cos x)/sin2x]dx
We know that sin2x= 2 sinx cos x)
-
- I = 0∫π/2log[(sinx. cos x)/(2 sinx cos x)]dx
- I = 0∫π/2 log(1/2)dx
- I = 0∫π/2 (log1-log 2)dx [Since, log (a/b) = log a- log b]
- I = 0∫π/2 -log 2 dx (value of log 1 = 0)
Now, take the constant – log 2 outside the integral,
-
- I = -log 2 0∫π/2dx
Now, integrate the function
-
- I = -log 2 [x]0π/2
Now, substitute the limits
-
- I = -log 2 [(π/2)-0]
- I = – log 2 (π/2)
- I = – (π/2) log 2 = R.H.S
Therefore, L.H. S = R.H.S
Hence. 0∫π/2 (2log sinx – log sin 2x)dx = – (π/2) log 2 is proved.
Example: solve ![]()
Solution:

Question. 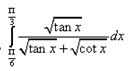
Solution:
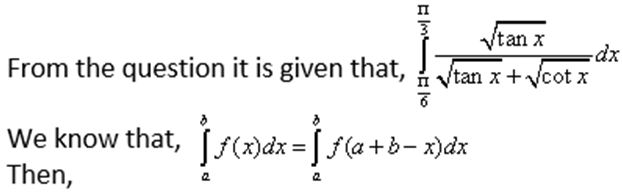

Now applying limits, we get,
2I = π/3 – π/6
2I = (2π – π)/6
2I = π/6
I = π/12
Question. 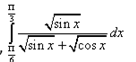
Solution:

Now applying limits, we get,
2I = π/3 – π/6
2I = (2π – π)/6
2I = π/6
I = π/12
Question. 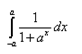
Solution:

Question. 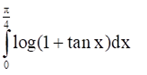
Solution:

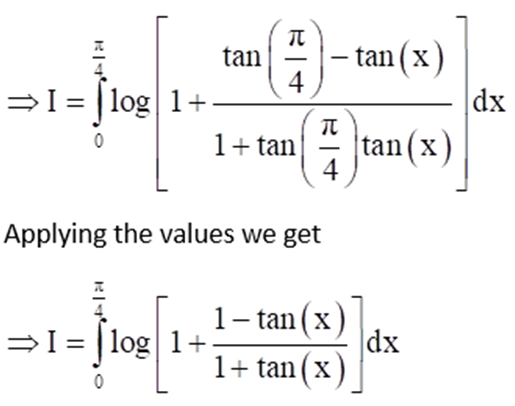


 KRISHNA PUBLICATIONS
KRISHNA PUBLICATIONS
