1. Conditional probability
- Books Name
- Mathmatics Book Based on NCERT
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 12
- Subject
- Mathmatics
Chapter 13
Probability
1.Conditional probability:
If E and F are two events associated with the same sample space ‘S’ of a random experiment,
The conditional probability of E given that F has already occurred,

Note that (1) is valid only when P(F) ≠ 0 i.e., F ≠ φ (Why?)
P(A|B) is the probability of event A occurring, given that event B occurs.
For example, given that you drew a red card,
what's the probability that it's a four (p(four|red))=2/26=1/13.
So out of the 26 red cards (given a red card), there are two fours
= 2/26=1/13.
Properties of conditional probability:
Let E and F be events of a sample space S of an experiment, then we have
Property 1.
P(S|F) = P(F|F) = 1
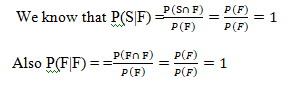
Thus P(S|F) = P(F|F) = 1
Property 2.
If A and B are any two events of a sample space S and F is an event of S such that P(F) ≠ 0,
then P((A ∪ B)|F) = P(A|F) + P(B|F) – P((A ∩ B)|F)
if A and B are disjoint events, then P((A∪B)|F) = P(A|F) + P(B|F)
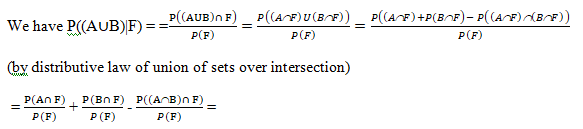
= P(A|F) + P(B|F) – P((A ∩B)|F)
When A and B are disjoint events, then P((A ∩ B)|F) = 0
⇒ P((A ∪ B)|F) = P(A|F) + P(B|F)
Property 3.
P(E′|F) = 1 − P(E|F) From Property 1,
we know that P(S|F) = 1 ⇒ P(E ∪ E′|F) = 1
since S = E ∪ E′ ⇒ P(E|F) + P (E′|F) = 1
since E and E′ are disjoint events
Thus, P(E′|F) = 1 − P(E|F)
Example 1.: If P(A) = 7 13 , P(B) = 9 13 and P(A ∩ B) = 4 13 , evaluate P(A|B).
Solution:
![]()
Example 2.: A family has two children. What is the probability that both the children are boys given that at least one of them is a boy ?
Solution: Let b stand for boy and g for girl.
The sample space of the experiment is S = {(b, b), (g, b), (b, g), (g, g)}
Let E and F denote the following events :
E : ‘both the children are boys’
F : ‘at least one of the child is a boy’
Then E = {(b,b)} and F = {(b,b), (g,b), (b,g)}
Now E ∩ F = {(b,b)}
Thus P(F) = 3/ 4 and P (E ∩ F )= 1/ 4
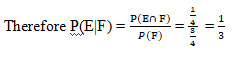
Example 3: Consider the experiment of tossing a coin. If the coin shows head, toss it again but if it shows tail, then throw a die. Find the conditional probability of the event that ‘the die shows a number greater than 4’ given that ‘there is at least one tail’.
Solution: S = {(H,H), (H,T), (T,1), (T,2), (T,3), (T,4), (T,5), (T,6)}
Let F be the event that ‘there is at least one tail’ and
E be the event ‘the die shows a number greater than 4’.
Then F = {(H,T), (T,1), (T,2), (T,3), (T,4), (T,5), (T,6)}
E = {(T,5), (T,6)} and
E ∩ F = {(T,5), (T,6)}
Now P(F) = P({(H,T)}) + P ({(T,1)}) + P ({(T,2)}) + P ({(T,3)}) + P ({(T,4)}) + P({(T,5)}) + P({(T,6)})
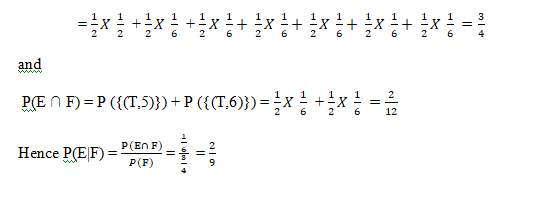
Example 1: Two dies are thrown simultaneously, and the sum of the numbers obtained is found to be 7. What is the probability that the number 3 has appeared at least once?
Solution: The sample space S would consist of all the numbers possible by the combination of two dies. Therefore S consists of 6 × 6, i.e. 36 events.
Event A indicates the combination in which 3 has appeared at least once.
Event B indicates the combination of the numbers which sum up to 7.
A = {(3, 1), (3, 2), (3, 3)(3, 4)(3, 5)(3, 6)(1, 3)(2, 3)(4, 3)(5, 3)(6, 3)}
B = {(1, 6)(2, 5)(3, 4)(4, 3)(5, 2)(6, 1)}
P(A) = 11/36
P(B) = 6/36
A ∩ B = 2
P(A ∩ B) = 2/36
Applying the conditional probability formula we get,
P(A|B) = P(A∩B)/P(B) = (2/36)/(6/36) = ⅓
Example 2: In a group of 100 computer buyers, 40 bought CPU, 30 purchased monitor, and 20 purchased CPU and monitors. If a computer buyer chose at random and bought a CPU, what is the probability they also bought a Monitor?
Solution: As per the first event, 40 out of 100 bought CPU,
So, P(A) = 40% or 0.4
Now, according to the question, 20 buyers purchased both CPU and monitors. So, this is the intersection of the happening of two events. Hence,
P(A∩B) = 20% or 0.2
By the formula of conditional probability we know;
P(B|A) = P(A∩B)/P(B)
P(B|A) = 0.2/0.4 = 2/4 = ½ = 0.5
The probability that a buyer bought a monitor, given that they purchased a CPU, is 50%.
![]()
2. multiplication theorem on probability
- Books Name
- Mathmatics Book Based on NCERT
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 12
- Subject
- Mathmatics
Multiplication theorem on probability
we can write
P(E ∩ F) = P(F) . P(E|F) ………….... (1)
P(E ∩ F) = P(E). P(F|E) ............... (2)
The above result is known as the multiplication rule of probability.
Multiplication rule of probability for more than two events If E, F and G are three events of sample space, we have P(E ∩ F ∩ G) = P(E) P(F|E) P(G|(E ∩ F)) = P(E) P(F|E) P(G|EF)
Example:
Three cards are drawn successively, without replacement from a pack of 52 well shuffled cards. What is the probability that first two cards are kings and the third card drawn is an ace?
Solution:
Let K denote the event that the card drawn is king and A be the event that the card drawn is an ace. Clearly, we have to find P (KKA) Now P(K) = 4 /52 Also, P (K|K) is the probability of second king with the condition that one king has already been drawn. Now there are three kings in (52 − 1) = 51 cards. Therefore P(K|K) = 3 /51 Lastly, P(A|KK) is the probability of third drawn card to be an ace, with the condition that two kings have already been drawn. Now there are four aces in left 50 cards.
Therefore P(A|KK) = 4 /50 By multiplication law of probability,
we have P(KKA) = P(K) P(K|K) P(A|KK) = (4/52) X (3/ 52) X (51/ 50) = 2/5525
3. independent events and mutually exclusive and exhaustive events
- Books Name
- Mathmatics Book Based on NCERT
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 12
- Subject
- Mathmatics
Independent events and mutually exclusive and exhaustive events
Definition 2.
Two events E and F are said to be independent,
if P(F|E) = P (F) provided P (E) ≠ 0 and P (E|F) = P (E) provided P (F) ≠ 0 Thus, in this definition we need to have P (E) ≠ 0 and P(F) ≠ 0
Now, by the multiplication rule of probability, we have P(E ∩ F) = P(E) . P (F|E) ……………. (1)
If E and F are independent, then (1)
becomes P(E ∩ F) = P(E) . P(F) ………………………….... (2)
Thus, using (2), the independence of two events is also defined as follows:
Mutually exclusive:
Two events E and F are said to be mutually exclusive if E ∩ F = ɸ
i.e., P(E ∩ F)=0
Exhaustive events
Two events E and F are said to be exhaustive events if E U F = S
i.e., P(E U F)=1
Definition 3. Let E and F be two events associated with the same random experiment, then E and F are said to be independent if P(E ∩ F) = P(E) . P (F)
Similarly for Three events.
Three events A, B and C are said to be mutually independent,
if P(A ∩ B) = P (A) P (B)
P(A ∩ C) = P (A) P (C)
P(B ∩ C) = P (B) P(C)
and P(A ∩ B ∩ C) = P (A) P (B) P (C)
Properties of Independent:
- If E and F are independent events, then the events E and F′ are independent.
- If E and F are independent events, then the events E’ and F are independent.
- If E and F are independent events, then the events E’ and F′ are independent.
Example . Prove that if E and F are independent events, then so are the events E and F′.
Solution : Since E and F are independent, we have P(E ∩ F) = P(E) . P(F) ....(1)
it is clear that E ∩ F and E ∩ F′ are mutually exclusive events
and also E =(E ∩ F) ∪ (E ∩ F′).
Therefore, P(E) = P(E ∩ F) + P(E ∩ F′)
- P(E ∩ F′) = P(E) − P(E ∩ F) = P(E) − P(E) . P(F) (by (1))
= P(E) (1−P(F)) = P(E). P(F′)
Hence, E and F′ are independent
Example . If A and B are two independent events, then the probability of occurrence of at least one of A and B is given by 1– P(A′) P(B′)
Solution: We have P(at least one of A and B) = P(A ∪ B)
P(A ∪ B) = P(A) + P(B) − P(A ∩ B) = P(A) + P(B) − P(A) P(B)
= P(A) + P(B) [1−P(A)] = P(A) + P(B). P(A′)
= 1− P(A′) + P(B) P(A′)
= 1− P(A′) [1− P(B)]
= 1− P(A′) P (B’)
Example . Prove that if E and F are independent events, then so are the events E’ and F.
Solution . Since E and F are independent, we have P(E ∩ F) = P(E) . P(F) ....(1)
it is clear that E ∩ F and E ‘∩ F are mutually exclusive events
and also E =(E ∩ F) ∪ (E’ ∩ F).
Therefore, P(E) = P(E ∩ F) + P(E’ ∩ F)
- P(E’ ∩ F) = P(F) − P(E ∩ F) = P(F) − P(E) . P(F) (by (1))
= P(F) (1−P(E)) = P(E’). P(F)
Hence, E’ and F are independent
4. Partitions,total probability, Bayes’ theorem
- Books Name
- Mathmatics Book Based on NCERT
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 12
- Subject
- Mathmatics
Partitions,total probability, Bayes’ theorem
Partition of a sample space
A set of events E1, E2, ..., En is said to represent a partition of the sample space S if
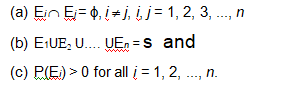
Theorem of total probability
Let {E1, E2,...,En} be a partition of the sample space S, and suppose that each of the events E1, E2,..., En has nonzero probability of occurrence. Let A be any event associated with S, then
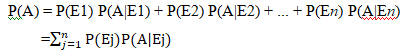
Proof: Given that E1, E2,..., En is a partition of the sample space S . Therefore,
S = E1 U E2 U ... U En and Ei Ç Ej = ɸ, i ¹ j, i, j = 1, 2, 3, ..., n
Now, we know that for any event A,
A = A ÇS
= A Ç (E1 U E2 U ... U En)
= (A Ç E1) U (AÇ E2) U ... U (AÇ En)
Also A ÇEi and A ÇEj are respectively the subsets of Ei and Ej .
We know that
Ei and Ej are disjoint, for i ¹ j , therefore, A Ç Ei and A Ç Ej are also disjoint for all
i ¹j, i, j = 1, 2, ..., n.
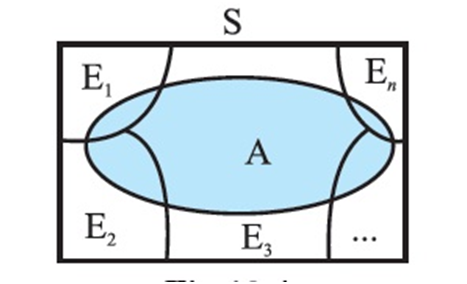
Thus, P(A) = P [(A Ç E1) U (AÇ E2) U ... U (AÇ En)]
= P (A Ç E1) + P (A Ç E2) + ... + P (A Ç En)
Now, by multiplication rule of probability,
we have
P(A Ç Ei) = SP(Ei) P(A|Ei) as P (Ei) > 0 "i = 1,2,..., n
Therefore, P (A) = P (E1) P (A|E1) + P (E2) P (A|E2) + ... + P (En)P(A|En)
![]()
Example : A person has undertaken a construction job. The probabilities are 0.65 that there will be strike, 0.80 that the construction job will be completed on time if there is no strike, and 0.32 that the construction job will be completed on time if there is a strike. Determine the probability that the construction job will be completed on time.
Solution : Let A be the event that the construction job will be completed on time, and B
be the event that there will be a strike. We have to find P(A).
We have
P(B) = 0.65, P(no strike) = P(B¢) = 1 - P(B) = 1 - 0.65 = 0.35
P(A|B) = 0.32, P(A|B¢) = 0.80
Since events B and B_ form a partition of the sample space S, therefore, by theorem
on total probability, we have
P(A) = P(B) P(A|B) + P(B¢) P(A|B¢)
= 0.65 × 0.32 + 0.35 × 0.8
= 0.208 + 0.28 = 0.488
Thus, the probability that the construction job will be completed in time is 0.488.
Bayes’ Theorem:
If E1, E2 ,..., En are n non empty events which constitute a partition of sample space S, i.e. E1, E2 ,..., En are pairwise disjoint and E1UE2U ... UEn = S and A is any event of nonzero probability, then
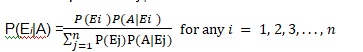
Proof: By formula of conditional probability, we know that

Hence Proved.
N.B.: -
- The events E1, E2, ..., En are called hypotheses.
- The probability P(Ei) is called the priori probability of the hypothesis Ei
- The conditional probability P(Ei |A) is called a posteriori probability of the
hypothesis Ei.
Example : Given three identical boxes I, II and III, each containing two coins. In
box I, both coins are gold coins, in box II, both are silver coins and in the box III, there
is one gold and one silver coin. A person chooses a box at random and takes out a coin.
If the coin is of gold, what is the probability that the other coin in the box is also of gold?
Solution Let E1, E2 and E3 be the events that boxes I, II and III are chosen, respectively.
Then P(E1) = P(E2) = P(E3) =![]()
Let A be the event that ‘the coin drawn is of gold’
Then P(A|E1) = P(a gold coin from bag I) = ![]()
P(A|E2) = P(a gold coin from bag II) = ![]() 0
0
P(A|E3) = P(a gold coin from bag III) =![]()
Now, the probability that the other coin in the box is of gold
= the probability that gold coin is drawn from the box I.
= P(E1|A)
By Bayes' theorem, we know that
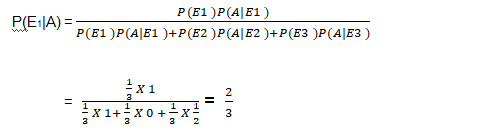
Example : A man is known to speak truth 3 out of 4 times. He throws a die and reports that it is a six. Find the probability that it is actually a six.
Solution: Let E be the event that the man reports that six occurs in the throwing of the die and let S1 be the event that six occurs and S2 be the event that six does not occur.
Then P(S1) = Probability that six occurs = ![]()
P(S2) = Probability that six does not occur = ![]()
P(E|S1) = Probability that the man reports that six occurs when six has
actually occurred on the die
= Probability that the man speaks the truth = ![]()
P(E|S2) = Probability that the man reports that six occurs when six has
not actually occurred on the die
= Probability that the man does not speak the truth = 1-![]() =
= ![]()
Thus, by Bayes' theorem, we get
P(S1|E) = Probability that the report of the man that six has occurred is
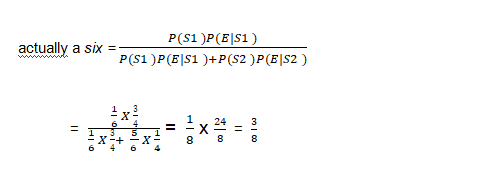
5. Random variable and its probability distribution
- Books Name
- Mathmatics Book Based on NCERT
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 12
- Subject
- Mathmatics
Random Variables and its Probability Distributions
Random Variables:
Definition : A random variable is a real valued function whose domain is the sample space of a random experiment.
Example: let us consider the experiment of tossing a coin two times in succession.
The sample space of the experiment is S = {HH, HT, TH, TT}.
If X denotes the number of heads obtained, then X is a random variable and for each outcome, its value is as given below :
X(HH) = 2, X (HT) = 1, X (TH) = 1, X (TT) = 0.
That means X= 0 1 2
Example : A person plays a game of tossing a coin thrice. For each head, he is given Rs 2 by the organizer of the game and for each tail, he has to give Rs 1.50 to the organiser. Let X denote the amount gained or lost by the person. Show that X is a random variable and exhibit it as a function on the sample space of the experiment.
Solution: X is a number whose values are defined on the outcomes of a random experiment. Therefore, X is a random variable.
Now, sample space of the experiment is
S = {HHH, HHT, HTH, THH, HTT, THT, TTH, TTT}
Then X(HHH) = Rs (2 × 3) = Rs 6
X(HHT) = X(HTH) = X(THH) = Rs (2 × 2 −1 × 1.50) = Rs 2.50
X(HTT) = X(THT) = (TTH) = Rs (1 × 2) – (2 × 1.50) = – Re 1
and X(TTT) = Rs (3 × 1.50) =-Rs 4.50
minus means loss and plus means gain.
X= {– 1, 2.50, – 4.50, 6}
Probability Distribution of the random variable X
Definition : The probability distribution of a random variable X is the system of numbers
X : x1 x2 x3 ... xn
P(X) : p(x1) p(x2) p(x3)... p(xn)
![]()
Example : Two cards are drawn successively with replacement from a well-shuffled deck of 52 cards. Find the probability distribution of the number of aces.
Solution: The number of aces is a random variable. Let it be denoted by X. Clearly, X can take the values 0, 1, or 2.
Now, since the draws are done with replacement, therefore, the two draws form independent experiments.
P(ace)= 4/52 = 1 / 13
P(non ace)= 48/52 = 12 / 13
Therefore,

Example : Let X denote the number of hours you study during a randomly selected school day. The probability that X can take the values x, has the following form, where k is some unknown constant.
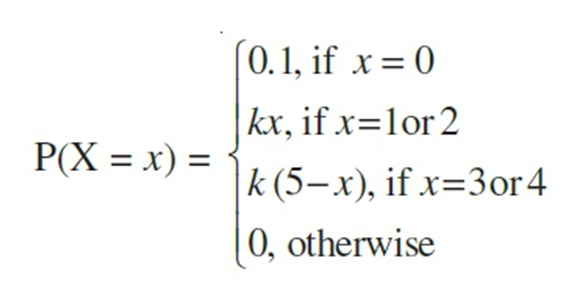
(a) Find the value of k.
(b) What is the probability that you study at least two hours ?
Exactly two hours?
At most two hours?
Solution: The probability distribution of X is
X: 0 1 2 3 4
P(X) 0.1 k 2k 2k k
(a) We know that
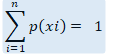
=> 0.1 + k + 2k + 2k + k = 1
=> k = 0.15
(b) P(you study at least two hours) = P(X ³2)
= P(X = 2) + P (X = 3) + P (X = 4)
= 2k + 2k + k = 5k = 5 × 0.15 = 0.75
P(you study exactly two hours) = P(X = 2)
= 2k = 2 × 0.15 = 0.3
P(you study at most two hours) = P(X £2)
= P (X = 0) + P(X = 1) + P(X = 2)
= 0.1 + k + 2k = 0.1 + 3k = 0.1 + 3 × 0.15
= 0.55
6. Binomial distribution , mean and variance of random variable
- Books Name
- Mathmatics Book Based on NCERT
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 12
- Subject
- Mathmatics
Binomial distribution , mean and variance of random variable
Mean of a random variable:
Definition : Let X be a random variable whose possible values x1, x2, x3, ..., xn occur with probabilities p1, p2, p3,..., pn, respectively. The mean of X, denoted by m, is the number
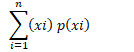
i.e. the mean of X is the weighted average of the possible values of X, The mean of a random variable X is also called the expectation of X, denoted by E(X).
![]()
Example : Let a pair of dice be thrown and the random variable X be the sum of the numbers that appear on the two dice. Find the mean or expectation of X.
Solution : The sample space of the experiment consists of 36 elementary events in the form of ordered pairs (xi, yi), where xi= 1, 2, 3, 4, 5, 6 and yi= 1, 2, 3, 4, 5, 6.
The random variable X i.e. the sum of the numbers on the two dice takes the values 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 or 12.

Thus, the mean of the sum of the numbers that appear on throwing two fair dice is 7.
Variance of a random variable:
Let X be a random variable whose possible values x1, x2,...,xn occur with
probabilities p(x1), p(x2),..., p(xn) respectively.
Let m= E (X) be the mean of X. The variance of X, denoted by Var (X) or ![]() x is defined as.
x is defined as.
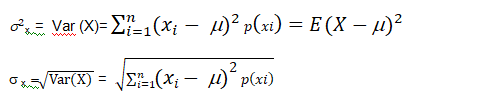
is called the standard deviation of the random variable X.
Bernoulli Trials and Binomial Distribution
Bernoulli trials:
Definition : Trials of a random experiment are called Bernoulli trials, if they satisfy the following conditions :
(i) There should be a finite number of trials.
(ii) The trials should be independent.
(iii) Each trial has exactly two outcomes : success or failure.
(iv) The probability of success remains the same in each trial.
Example : Six balls are drawn successively from an urn containing 7 red and 9 black balls. Tell whether or not the trials of drawing balls are Bernoulli trials when after each draw the ball drawn is
(i) replaced (ii) not replaced in the urn.
Solution:
(i) The number of trials is finite. When the drawing is done with replacement, the probability of success (say, red ball) is p =7/16
which is same for all six trials (draws). Hence, the drawing of balls with replacements are Bernoulli trials.
(ii) When the drawing is done without replacement, the probability of success
(i.e., red ball) in first trial is 7/16 , in 2nd trial is 6/15
if the first ball drawn is red or 7/15
if the first ball drawn is black and so on. Clearly, the probability of success is not same for all trials, hence the trials are not Bernoulli trials.
Binomial distribution:
The binomial distribution formula is for any random variable X, given by;

Where,
n = the number of experiments
x = 0, 1, 2, 3, 4, …
p = Probability of Success in a single experiment
q = Probability of Failure in a single experiment = 1 – p
The binomial distribution formula can also be written in the form of n-Bernoulli trials, where nCx = n!/[x!(n-x)!]. Hence,
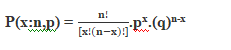
Binomial Distribution Mean and Variance
Binomial distribution, the mean, variance and standard deviation for the given number of success are represented using the formulas
Mean, μ = np
Variance, σ2 = npq
Standard Deviation σ= √(npq)
Where p is the probability of success
q is the probability of failure, where q = 1-p
Properties of Binomial Distribution
The properties of the binomial distribution are:
- There are two possible outcomes: true or false, success or failure, yes or no.
- There is ‘n’ number of independent trials or a fixed number of n times repeated trials.
- The probability of success or failure varies for each trial.
- Only the number of success is calculated out of n independent trials.
- Every trial is an independent trial, which means the outcome of one trial does not affect the outcome of another trial.
Example 1: If a coin is tossed 5 times, find the probability of:
(a) Exactly 2 heads
(b) At least 4 heads.
Solution:
(a) The repeated tossing of the coin is an example of a Bernoulli trial. According to the problem:
Number of trials: n=5
Probability of head: p= 1/2 and hence the probability of tail, q =1/2
For exactly two heads:
x=2
P(x=2) = 5C2 p2 q5-2 = 5! / 2! 3! × (½)2× (½)3
P(x=2) = 5/16
(b) For at least four heads,
x ≥ 4, P(x ≥ 4) = P(x = 4) + P(x=5)
Hence,
P(x = 4) = 5C4 p4 q5-4 = 5!/4! 1! × (½)4× (½)1 = 5/32
P(x = 5) = 5C5 p5 q5-5 = (½)5 = 1/32
Therefore,
P(x ≥ 4) = 5/32 + 1/32 = 6/32 = 3/16
Example 2: For the same question given above, find the probability of:
a) Getting at least 2 heads
Solution: P (at most 2 heads) = P(X ≤ 2) = P (X = 0) + P (X = 1)
P(X = 0) = (½)5 = 1/32
P(X=1) = 5C1 (½)5.= 5/32
Therefore,
P(X ≤ 2) = 1/32 + 5/32 = 3/16
Example 3:
A fair coin is tossed 10 times, what are the probability of getting exactly 6 heads and at least six heads.
Solution:
Let x denote the number of heads in an experiment.
Here, the number of times the coin tossed is 10. Hence, n=10.
The probability of getting head, p ½
The probability of getting a tail, q = 1-p = 1-(½) = ½.
The binomial distribution is given by the formula:
P(X= x) = nCxpxqn-x, where = 0, 1, 2, 3, …
Therefore, P(X = x) = 10Cx(½)x(½)10-x
(i) The probability of getting exactly 6 heads is:
P(X=6) = 10C6(½)6(½)10-6
P(X= 6) = 10C6(½)10
P(X = 6) = 105/512.
Hence, the probability of getting exactly 6 heads is 105/512.
(ii) The probability of getting at least 6 heads is P(X ≥ 6)
P(X ≥ 6) = P(X=6) + P(X=7) + P(X= 8) + P(X = 9) + P(X=10)
P(X ≥ 6) = 10C6(½)10 + 10C7(½)10 + 10C8(½)10 + 10C9(½)10 + 10C10(½)10
P(X ≥ 6) = 193/512.

 KRISHNA PUBLICATIONS
KRISHNA PUBLICATIONS
