1. General characteristics of solid state
- Books Name
- ACME SMART COACHING Chemistry Book
- Publication
- ACME SMART PUBLICATION
- Course
- CBSE Class 12
- Subject
- Chemistry
Chapter 1
solid state
Solids are characterised by the state of matter in which particles are closely packed and held together by strong inter molecular attractive force.
General Characteristics / Properties of Solids
(a) In solid state the particles are not able to move randomly.
(b) They have definite shape and volume.
(c) Solids have high density.
(d) Solids have high and sharp melting point which is depend on the strength or value of binding energy.
(e) They are very low compressible.
(f) They show very slow diffusion.
2. Amorphous and crystalline solids
- Books Name
- ACME SMART COACHING Chemistry Book
- Publication
- ACME SMART PUBLICATION
- Course
- CBSE Class 12
- Subject
- Chemistry
Types of Solids (Amorphous/Crystalline)

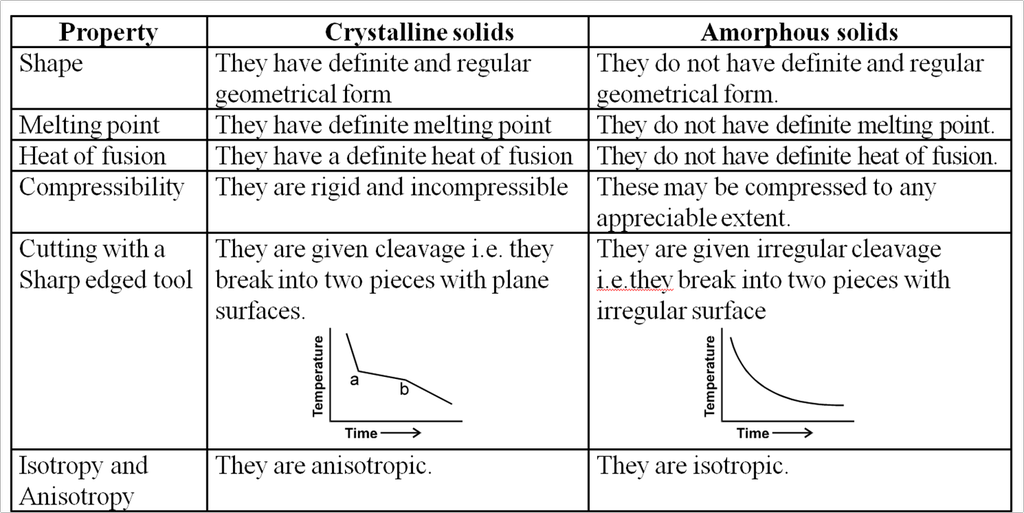
Crystalline solids :
(a) In this type of solids the atoms or molecule are arranged in a regular pattern in the three dimensional network.
(b) They have well defined geometrical pattern, sharp melting point, definite heat of fusion and anisotropic nature.
(c) Anisotropic means they exhibit different physical properties in all directions.
e.g. The electrical and thermal conductivities are different directions.
(d) They are generally incompressible.
(e) The general examples of crystalline solids are as Quartz, diamond etc.
Amorphous Solids :
(a) In this type of solids, the arrangement of building constituents is not regular.
(b) They are regarded as super cooled liquids with high viscosity in which the force of attraction holding the molecules together are so great, that the material becomes rigid but there is no regularity in structure.
(c) They do not have sharp melting points.
(d) They are isotropic as they exhibit same physical properties in all the directions.
(e) The general examples of this solids are as glass, Rubber, plastics etc.
Difference between crystalline and amorphous solids :
3. Classification of crystalline solids
- Books Name
- ACME SMART COACHING Chemistry Book
- Publication
- ACME SMART PUBLICATION
- Course
- CBSE Class 12
- Subject
- Chemistry
Classification of crystalline solids
STUDY OF CRYSTALS :
Crystal : A crystal is a homogeneous portion of a solid substance made by regular pattern of structural units bonded by plane surface making definite angles with each other.
Space lattice : The arrangement of constituents like atom, ions and molecules in different sites in three dimensional space is called space lattice.
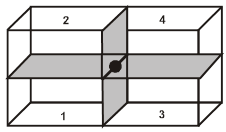
Unit cell : The smallest repeating unit in space lattice which when repeats over and over again, results in a crystal of the given substance called unit cell.
Properties of a cube :
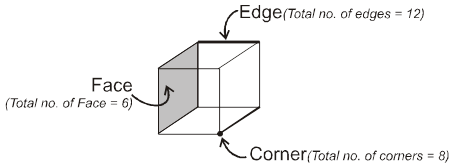
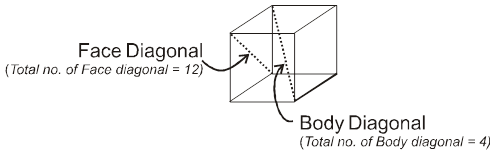
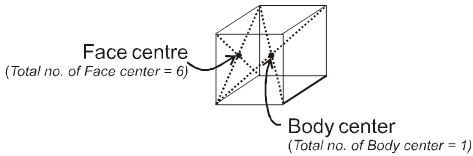
Face : The plane surface of the crystal are called faces.
Edge : An edge is formed by the intersection of two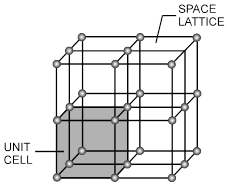 adjacent faces.
adjacent faces.
Interfacial angles : The angle between the perpendiculars two intersecting faces called interfacial angles.
Unit Cell in two dimensions :
![]()
Now in order to uniquely explain a regular arrangement in two dimensions we need the help of three parameters, two distance parameters and one angular parameter. Based upon their different relationships we can define different cases
Case ‘A’ (a = b) angle = 90º

The unit cell in such a case is a square. such square side by side we will obtain the entire two dimensional arrangement.
Case ‘B’(a ¹ b) angle = 90º

Placing The unit cell formed in this case is a rectangle.
Unit cell in three dimensions :
It has six parameters, 3-distance parameters and 3-angular parameter.
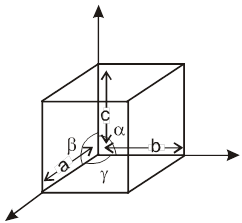
a, b, c are lengths of unit cell (also known as the crystallographic axes). a, b, g are known as the crystallographic angles.
4. Different Classes of Crystals
- Books Name
- ACME SMART COACHING Chemistry Book
- Publication
- ACME SMART PUBLICATION
- Course
- CBSE Class 12
- Subject
- Chemistry
DIFFERENT CLASSES OF CRYSTALS
Based on different permutations of a, b, c and a, b, g we define different crystal classes.
Seven Crystal System
Table : 4

Hint for memorise : CaTORacHMT
Note : In 3-D 14 different types of unit cell are found and these are also known as 14 Bravais lattice.
Types of unit cell :
In every crystal class, the positioning of the lattice points may be different. Based upon these different positions occupied by the lattice points, we have different types of unit cells.
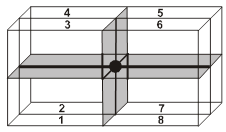
1. Simple / primitive type of unit cell : If lattice points or the particles of the solid are present only at the corners of the unit cell.
2. Body centred unit cell : lattice point are at the corners as well as at the body centre.
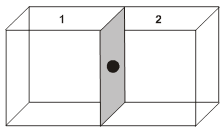
3. Face centred unit cell : lattice points are at corners as well as at each of the face centres.
4. End centred unit cell : lattice points are at the corners as well as at centre of any of two opposite faces.
Each of these arrangements corresponds to a unique and different type of arrangement.These 14 different arrangements are called the 14 Bravais lattices.
In any lattice, the surrounding of each and every lattice point is exactly identical
5. Mathematical Calculations of Cubic System
- Books Name
- ACME SMART COACHING Chemistry Book
- Publication
- ACME SMART PUBLICATION
- Course
- CBSE Class 12
- Subject
- Chemistry
MATHEMATICAL ANALYSIS OF CUBIC SYSTEM
(TYPES AND ANALYSIS)
Simplest crystal is to be studied in cubic system. Three types of cubic systems are following.
(a) Simple Cubic (SC) : Atoms are arranged at the corners of the cube.
(b) Body Centered Cubic (BCC) : Atoms are arranged at the corners and at the centre of the cube.
(c) Face Centered Cubic (FCC) : Atoms are arranged at the corners and at centered of the each faces.
Contribution of different Lattice point in one Cubical unit cell :
(i) Contribution from one corner lattice point =![]() th.
th.
(ii) Contribution from one face centered lattice point =![]() .
.
(iii) Contribution from edge centered lattice point = ![]() th.
th.
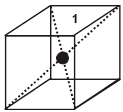
(iv) Contribution from body centered lattice point = 1.
Number of atoms per unit cell / unit cell contents :
The total number of atoms contained with in the unit cell for a simple cubic called the unit cell content.
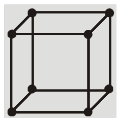
(a) Simple cubic structure (sc) :
Each corner atom is shared by eight surrounding cubes. Therefore, it contributes for ![]() of an atom.
of an atom.
![]()
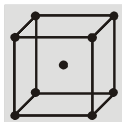
(b) Body centered cubic structure (bcc) :
(i) Eight Corner atoms contribute one atom per unit cell.
(ii) Centre atom contribute one atom per unit cell.
(iii) So, total 1 + 1 = 2 atoms per unit cell.
![]()
(c) Face centered cubic structure (fcc) :
(i) The eight corners atoms contribute for ![]() of an atom and thus one atom per unit cell.
of an atom and thus one atom per unit cell.
(ii) Each of six face centered atoms is shared by two adjacent unit cells and therefore one face centred atom contribute half of its share. Means
![]() atom per unit cell.
atom per unit cell. 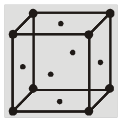
(iii) So, total Z = 3 + 1 = 4 atoms per unit cell.
Atomic radius :
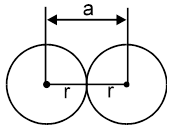
It is defined as the half of the distance between nearest neighbouring atoms in a crystal. It is expressed in terms of length of the edge (a) of the unit cell of the crystal.
(a) Simple cubic structure [S.C.]
Radius of atom ‘r’ =![]()
(b) Face centered cubic structure (FCC) ‘r’ = ![]()
(c) Body centered cubic structure (BCC) ‘r’ =![]()
a = b = c
a = b = g = 90º
6. Arrangement of the atom / particles of the solids in three dimensions
- Books Name
- ACME SMART COACHING Chemistry Book
- Publication
- ACME SMART PUBLICATION
- Course
- CBSE Class 12
- Subject
- Chemistry
Arrangement of the atom / particles of the solids in three dimensions
Now having gained a knowledge of some of the terms, let us study how the different arrangements in space are brought about.
Firstly we will focus our attention on the solids containing only one type of lattice points.
The solids which contain only one type of lattice points are:
- metallic solids (eg. Iron)
- molecular solids (eg. dry ice)
- covalent network solids (eg. diamond)
(Ionic solids do not fall into this category as they contain more than one type of particles,they will be studied in the later parts of the chapter)
All the atoms or particles of the solids will be represented by solid spheres, each of radius ‘r’.
We will be taking these spheres of radius ‘r’ and explore how we can arrange these in three dimensions.Firstly we will begin with arrangement in one dimension.
Arrangement in 1-D : In one dimension it is possible to arrange the spheres in two possible ways.
1. 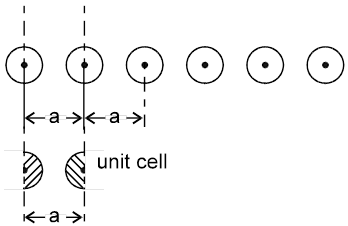
Not Stable [because the potential energy of the system is not minimum]
2. 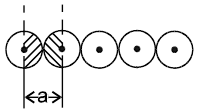 a = 2r
a = 2r
Coordination number = 2
1-D close packing stable arrangement
This is the predominant way of packing in one dimension and as such most of the space lattices will show such an arrangement in one dimension along the planes of close packing.
Arrangement in two dimension :
In two dimensions also there are two ways of packing the spheres(in moving from one dimension to two dimensions it can be imagined that the two dimensional array will be made up of 1-D closed pack arrays / lines which are stacked one on top of other.
1. Square packing : If the one dimensional arrays are placed on top of one another, we get the square packing in two dimensions.
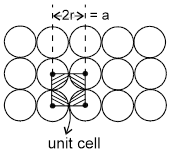
One sphere will be in contact with 4 other spheres.
area of square = a2 = 4r2
area of atoms in the square = ![]()
fraction of area occupied by spheres = 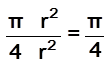 = 78%
= 78%
2. Hexagonal close packing : (in 2-D) If in a two dimensional arrangement,every one dimensional array is placed in the cavity of the just preceding array, we get the hexagonal packing in two dimensions.
area of hexagon = ![]()
area of atoms = ![]()
fraction of area occupied =![]()
As is evident from the above calculations, the spheres are in closer contact in the hexagonal arrangement, hence the hexagonal arrangement is considered to be a better way of packing as compared to the square packing.
Arrangement in three Dimensions :
1. Simple cubical arrangement in three dimensions :
(will be made up of 2-D sheets arranged one over other)
The simple cubical packing is obtained by arranging the square pack sheets of two dimension one over the other such that spheres of the second sheet are exactly (vertically) above the spheres of first sheet.
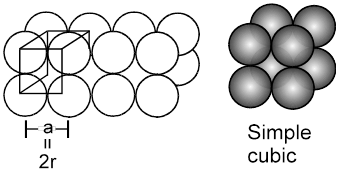
(Note that ![]() , hence crystal thus formed will belong to the cubic crystal class, and as the lattice points are only at the corners, hence the unit cell will be simple, therefore what we get is the simple cubic)
, hence crystal thus formed will belong to the cubic crystal class, and as the lattice points are only at the corners, hence the unit cell will be simple, therefore what we get is the simple cubic)
(i) Relation between ‘a’ and ‘r’
a = 2r (because atoms along the edge are touching each other)
(ii) Effective no. of atoms per unit cell :
(Z) = × 8 = 1
(iii) Packing fraction :
Packing efficiency = ![]()
= 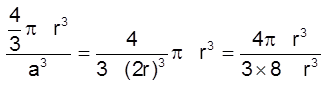 = 0.52 (or 52%)
= 0.52 (or 52%)
(Note : This is not a very efficient way of packing as the packing fraction is very low)
(iv) Coordination Number :

It is defined as the number of atoms touching any one particular atom. For simple cubic, coordination number = 6.
(v) Density of unit cell : It is the ratio of mass of the spheres present in unit cell and total volume of unit cell.
Density of the unit cell = ![]()
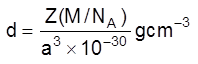 Þ
Þ 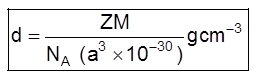
Where Z = no. of atoms in a unit cell
M/NA = mass of a single atom
M = molar mass
NA = Avogadro number (6.023 × 1023)
2. Body centred cubic :
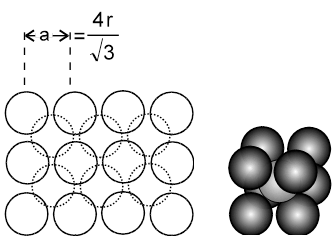
The body centred cubic is a unique way of packing, as the 2D-arrays that can be imagined to constitute the space lattice are themselves formed in a unique way. The lattice points in the 2D array do not touch each other. The spheres start touching each other only upon moving from 2D to 3D, i.e when the 2D arrays are placed on top of each other in such a fashion that the spheres of the next plane are into the cavities of the first plane of spheres.The third plane of spheres is then exactly identical to the first plane of spheres.
(i) a ¹ 2r (as atoms along the edge are not touching each other)
they touch along the body diagonal, hence ![]() a = 4r.
a = 4r.
(ii) Effective number of atoms (Z) = 1 + ![]() × 8 = 2.
× 8 = 2.
(iii) Packing fraction = 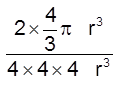
![]() =
= 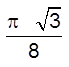 0.68 = 68%
0.68 = 68%
(iv) Coordination No.= 8
(the sphere at the body centre will be touching the spheres at the eight corners)
(v) Density = 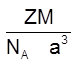 =
= ![]() (Q Z = 2)
(Q Z = 2)
3. Close packing in three dimensions :

(These are made up of two dimensional hexagonally packed sheets) In second layer we have two kinds of voids.
(i) Voids of second layer below which there are spheres of first layer (all voids of type ‘a’).
(ii) Voids of second layer below which there are voids of first layer (all voids of type ‘b’).
For third layer, we have two possibilities.
(A) If spheres of IIIrd layer are placed in voids of IInd layer below which there are spheres of Ist layer (voids of type ’a’) then Ist layer and IIIrd layer are identical so this is called AB–AB pattern repeat or hexagonal close packing)
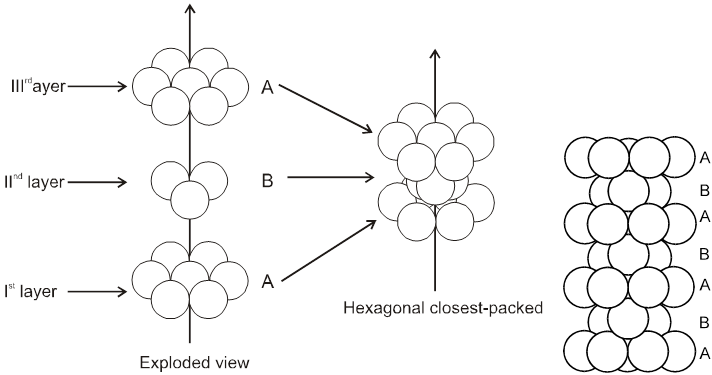
Hcp unit cell : a = 2r = b
(i) Calculation of ‘c’ :
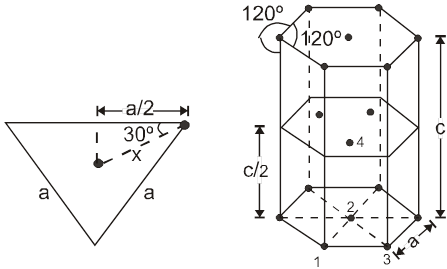
For the estimation of ‘c’, consider the spheres marked 1,2,3,4 in the unit cell as shown.These four spheres form a regular tetrahedron. The length of the perpendicular from ‘4’ to the equilateral triangle 1-2-3 will be equal to c/2.
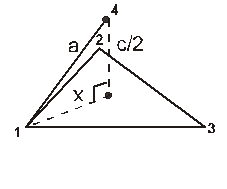 cos 30º =
cos 30º = ![]()
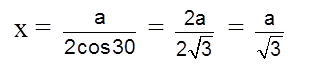
Apply pythagoras theorem.
x2 + (c/2)2 = a2 Þ c = ![]() 4r
4r
Volume of the hexagon = Area of base x Height.
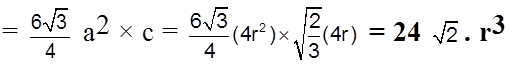
(ii) Effective no. of atoms per unit cell :
Z = ![]() × (no. of atoms at corner) +
× (no. of atoms at corner) + ![]() × (no. of atoms at face centres) + 1 × (no. of atoms inside the body)
× (no. of atoms at face centres) + 1 × (no. of atoms inside the body)
= ![]() × 12 +
× 12 + ![]() × 2 + 1 × 3 = 2 + 1 + 3 = 6
× 2 + 1 × 3 = 2 + 1 + 3 = 6
Packing fraction : 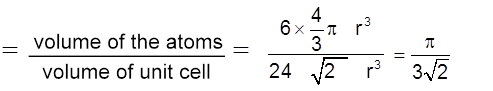 = 0.74 = 74%
= 0.74 = 74%
Coordination No. : C.N. = 12
Density ![]() (Q Z = 6)
(Q Z = 6)
(B) ABC-ABC arrangement :
If the third layer spheres are placed in those voids of second layer under which there are voids of the first layer of spheres (voids of type ‘b’), then the first and the third layer of spheres will not be identical.Such an arrangement will lead to an ABC-ABC type of arrangement.It is also known as the cubical close packing (ccp) or also as the Face Centred Cubic structure (FCC).
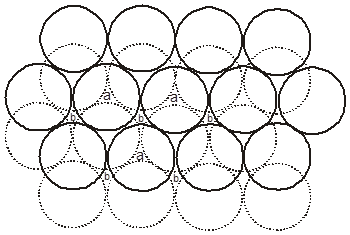
(a = tetrahedral voids)
(b = octahedral voids)
In the ABC – ABC pattern, the spheres of 4th layer are vertically above the spheres of Ist layer then these consecutive layers are different from each other, fourth layer will be idential to first layer so it will be called ABC – ABC repeat pattern.It is also called the ccp (cubical close packing) because a cubical type of unit cell is used for the study of this arrangement.

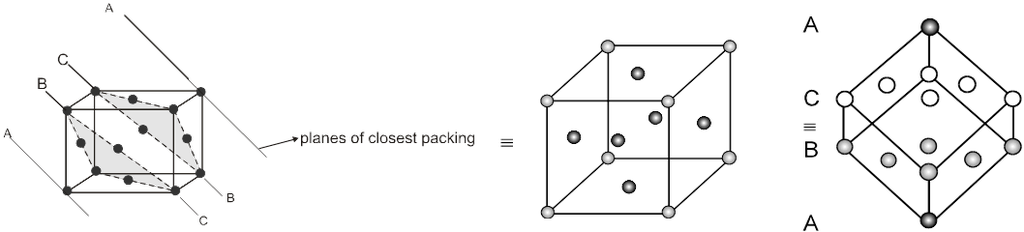
(i) Relation between ‘a’ and ‘r’ :
a ¹ 2r
![]() (as the spheres touch along the face diagonal)
(as the spheres touch along the face diagonal)
(ii) Effective no. of atoms :
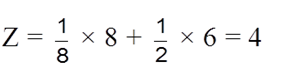
(iii) Packing fraction : 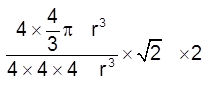 =
= ![]() = 0.74 = 74%
= 0.74 = 74%
(iv) Coordination number : 12
(v) Density![]()
Note : In close packings, whenever two consecutive layers are of different kinds(FCC, HCP) then packing efficiency will always be 74%
7. Types of voids found in close packing
- Books Name
- ACME SMART COACHING Chemistry Book
- Publication
- ACME SMART PUBLICATION
- Course
- CBSE Class 12
- Subject
- Chemistry
TYPES OF VOIDS FOUND IN CLOSE PACKING
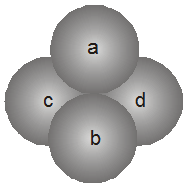
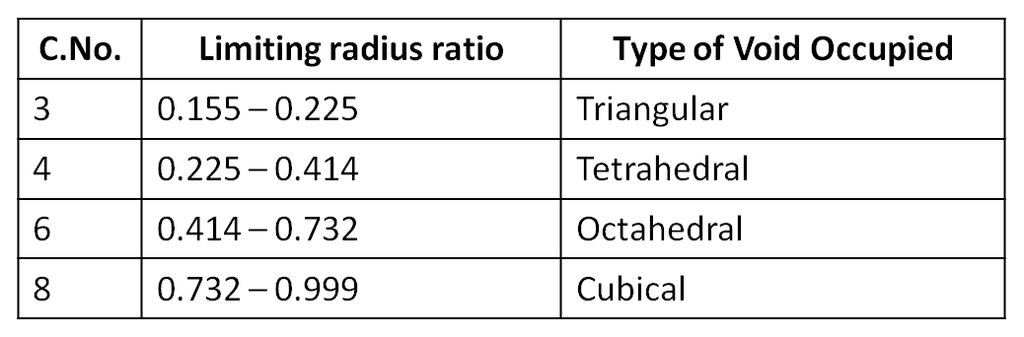
1. Tetrahedral void (3-Dimensional 4 co-ordinate) :
The tetrahedral void is formed whenever a sphere is placed on top of the triangular arrangement as in case of the triangular void.
r = 0.225 R
Location of tetrahedral voids in FCC unit cell :
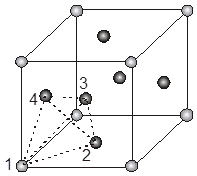
The FCC unit cell has eight tetrahedral voids per unit cell. Just below every cornerof the unit cell, there is one. As there are eight corners, there are eight tetrahedral voids.
The spheres 1, 2, 3, 4 form a tetrahedral void.
2. Octahedral void (3-Dimensional 6 coordinate void) The octahedral void is formed whenever two spheres are placed, one on top and the other below a square arrangement of spheres
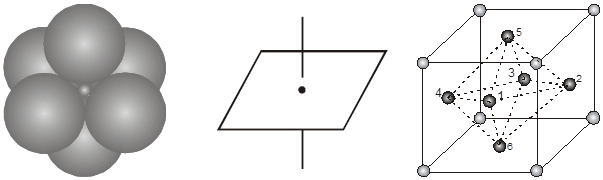
r = 0.414 R 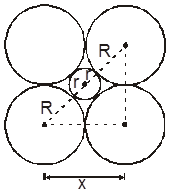
Location of octahedral voids in a FCC unit cell :
In a FCC unit cell, there are four octahedral voids. They are present at all the edge centres and at the body centre. The contribution of the edge centre void per unit cell is ![]() .
.
Hence, total number of octahedral voids = 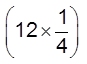 + (1) = 4
+ (1) = 4
edge centres body centre
Note : Let the no. of close packed spheres be N then the no. of octahedral void gemetrated = N and the number of tetrahedral void generated = 2N
3. Cubical void (3-Dimensional 8-coordinate void)
The cubical void is generally not found in closed packed structures, but is generated as a result of distortions arising from the occupancy of voids by larger particles.
Along body diagonal
r = 0.732 R
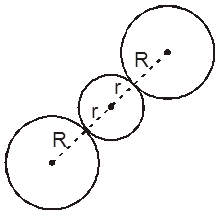
IONIC SOLIDS :
Ionic solids are characterised by the presence of atleast two types of particles,viz: the cation and the anion,even the simplest of ionic solids contains one cation and one anion.
The Cations are generally found to be of smaller size, and the anions of larger sizes. The anions thus form the lattice by occupying the lattice positions and the cations are found inside the voids in such structures.
The types of void occupied by the cation would depend upon the the ratio of its radius to that of the anion, popularly termed as the radius ratio. Hence, radius ratio = r+ / r–
Examples of ionic crystals :
(a) Rock Salt (NaCl) Coordination number (6 : 6) NaCl crystallizes in the face centred cubic structure. The chloride ions are present at all the lattice position and the sodium ions occupy all the octahedral voids.
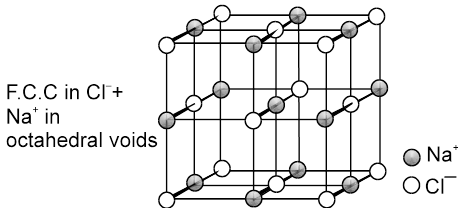
Every sodium is in contact with four chloride ions, and every chloride is in contact with four sodium ions
(b) CsCl C.No. (8 : 8)
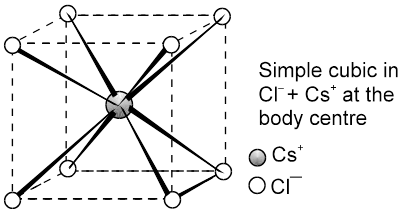
The cesium ion is at the body centre and the chloride ions are at the corners.
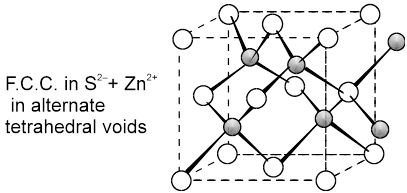
(c) Zinc Blend (ZnS) C.No. (4 : 4)
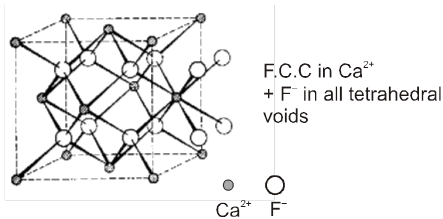
(d) Fluorite structure (CaF2) C.No. (8 : 4)
8. Crystals defects (Point Defects)
- Books Name
- ACME SMART COACHING Chemistry Book
- Publication
- ACME SMART PUBLICATION
- Course
- CBSE Class 12
- Subject
- Chemistry
CRYSTALS DEFECTS (POINT DEFECTS)
Imperfection can be because of :
– Conditions under which crystals have been developed.
– Impurities
– Temp (because of thermal conductivity some atoms/ions can get displaced
These imperfections can be
(a) Point defects – defects will be only at certain lattice positions.
(b) Line defects – If atoms/ions are misplaced/missing/replaced by some other ions along a line
(c) Plane (screw) defects – If atoms/ions are misplaced/missing/replaced by some other ions along a line in a plane.
Types of point defects
Point defect can be classified into three types :
(a) stoichiometric defects
(b) impurity defects
c) non-stoichiometric defect
(a) Stoichiometric defect
These are the point defects that do not distrub the stoichiometry of the solid. They are also called intrinsic ot thermodynamic defects. basically these are two types. Vacancy defecs and interstitial defects.
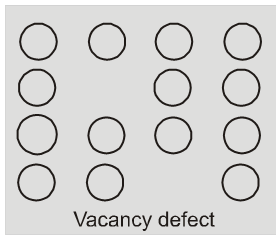
(i) Vacancy defect : When some of the lattice site are vacant, the crystal is said to have vacancy defect. This results in decrease in density of the substance. This defect can also develop when a substance is heated.
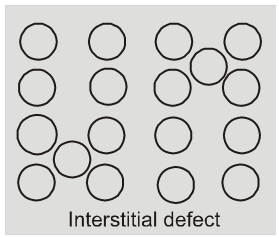
(ii) Interstitial defect : When some constituent particles (atoms or molecules)
occupy an interstitial site. the crystal is said to have interstitial defect. This defect increases the density of the substance.
Vacancy and interstitial defects as explained above can be shown by non ionic solids. Ionic solids must always maintain electrical neutrality.
Rather than simple vacancy or interstitial defects, they show these defects as Frenkel and schottky defects.
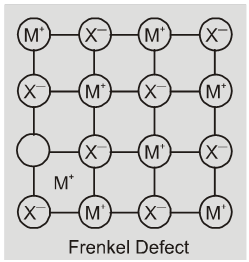
(iii) Frenkel defect : This defect is shown by ionic solids. The smaller ion
(usually cation) is dislocated from its normal site to an interstitial site. It creates a vacancy defect at its original site and an interstitial defect at its new location.
Frenkel defect is also called dislocation defect. It does not change the density of the solid. Frenkel defect is shown by ionic substance in which there is a large difference in the size of ions, for example, ZnS, AgCl,AgBr and AgI due to small size of Zn2+ and Ag+ ions.
Eg. ZnS, AgCl, AgBr, AgI etc.
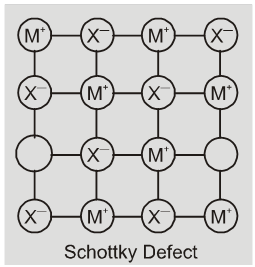
(iv) Schottky defect : It is basically a vacancy defect in ionic solids. In order
to maintain electrical netrality. The number of missing cations and anions are equal.
Like simple vacancy defect, schottky defect also decreases the density of the substance, Number of such defects in ionic solids is quite significant. For example, in NaCl there are approximately 106 schottky pairs per cm3 at room temperature. In 1 cm3 there are about 1022 ions. Thus, there is one schottky defect per 1016 ions. Schottky defect is shown by ionic substance in which the cation and anion are of almost similar sizes. For example,NaCl, KCl, CsCl and AgBr.
Note : It may be noted that AgBr shows both, Frenkel as well as schottky defects.
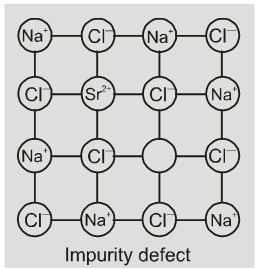
(b) Impurity defects
If molten NaCl containing a little amount of SrCl2 is crystallised, some of
the sites of Na+ ions are occupied by Sr2+. Each Sr2+ replaces two Na+ ions. It occupies the site of one ion and the other site remains vacant. The cationic vacancies thus produced are equal in number is the solid solution of CdCl2 and AgCl.
(c) Non-stoichiometric defect
The defects discussed so far do not disturb the stoichiometry of the crystalline substance. However a large number of non-stoichiometric inorganic solids are known which contain the constituent elements in non-stoichiometric ratio due to defects in their crystal structures. These defects are of two types :
(i) metal excess defect and (ii) metal deficiency defect.
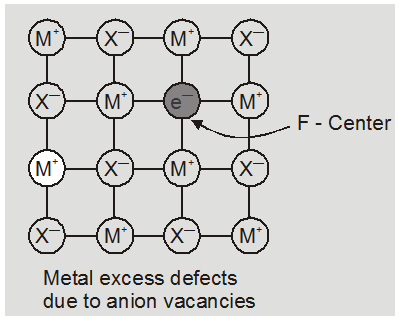
(i) metal excess defect
(a) metal excess defect due to anionic vacancies : Alkali halides like NaCl and KCl show this type of defect. When crystals of NaCl are heated in an atmosphere of sodium vapours, the sodium atoms are deposited on the surface of the crystal. The Cl– ions diffuse to the surface of the crystal and combine with Na atoms to give NaCl. This happens by loss of electron by sodium atoms to form Na+ ions. The released electrons diffuse into the crystal and occupy anionic site. As a result the crystal and now has an excess of sodium. The anionc sites occupied by unpaired electrons are called F-centres (from german word farbenzenter for colour centre). They impart yellow colour to the
crystals of NaCl. The colour results by excitation of these electrons when they absorb energy from the visible light falling on the crystals.
Eg. :
* The excess sodium in NaCl makes the crystal appears yellow.
* Excess potassium in KCl makes it violet.
* Excess lithium in LiCl makes it pink.
Greater the number of F-centres greater is the intensity of colour. This type of defects are found in crystal which are likely to possess schottky Defects.
(b) metal deficiency defect due to the presence of extra cations at interstitial sites : Zinc oxideis white in colour at room temperature. On heating it loses oxygen and turns yellow.
![]()
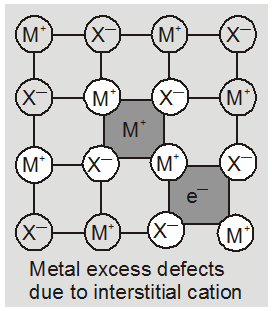
Now there is excess of zinc in the crystal and its formula becomes Zn1+xO. The excess Zn2+ ions move to interstitial sites and the electrons to neghbouring interstitial sites.
(ii) metal deficiency defect : There are many solids which are difficult to prepare in the stoichiometric composition and contain less amount of the metal as compared to the stoichiometric proportion. A typical example of this type is FeO which is mostly found with a composition of Fe0.95O. it may actually range from Fe0.93O to Fe0.96O. In crystals of FeO some Fe2+ cations are missing and the loss of positive charge is made up by the presence of required number of Fe3+ ions.
9. Properties of Solids
- Books Name
- ACME SMART COACHING Chemistry Book
- Publication
- ACME SMART PUBLICATION
- Course
- CBSE Class 12
- Subject
- Chemistry
PROPERTIES OF SOLIDS
1. Electric Properties :
On the basis of electrical conductivity the solids can be broadly classified into the three types:
(a) Metals (conductors)
(b) Insulators
(c) Semi-conductors.
Following are salient features of electrical conductance in solids.
(i) The electrical conductivity of metallic conductors is due to the motion of electrons or positive holes (electronic conductivity) or through the motion of ions (ionic conductivity)
(ii) The conductance through electrons is called n-type conduction and through positive holes is called p-type conduction.
(iii) The conductance in insulators and semiconductors is mainly due to the presence of interstitial electrons and positive holes in the solids due to imperfections.
(iv) The conductivity of semiconductors and insulators increases with increase in temperature while that of metals decreases.
(v) Electrical conductivity of metal is in the order of 106–108 ohm–1 cm–1 while that of inculator is of the order of 10–12 ohm–1 cm–1. Semiconductors have intermediate value in the range 10–9 ohm–1 cm–1.
2. Magnetic Properties :
Based on the behaviour of substances when placed in the magnetic field, they are classified into five classes.

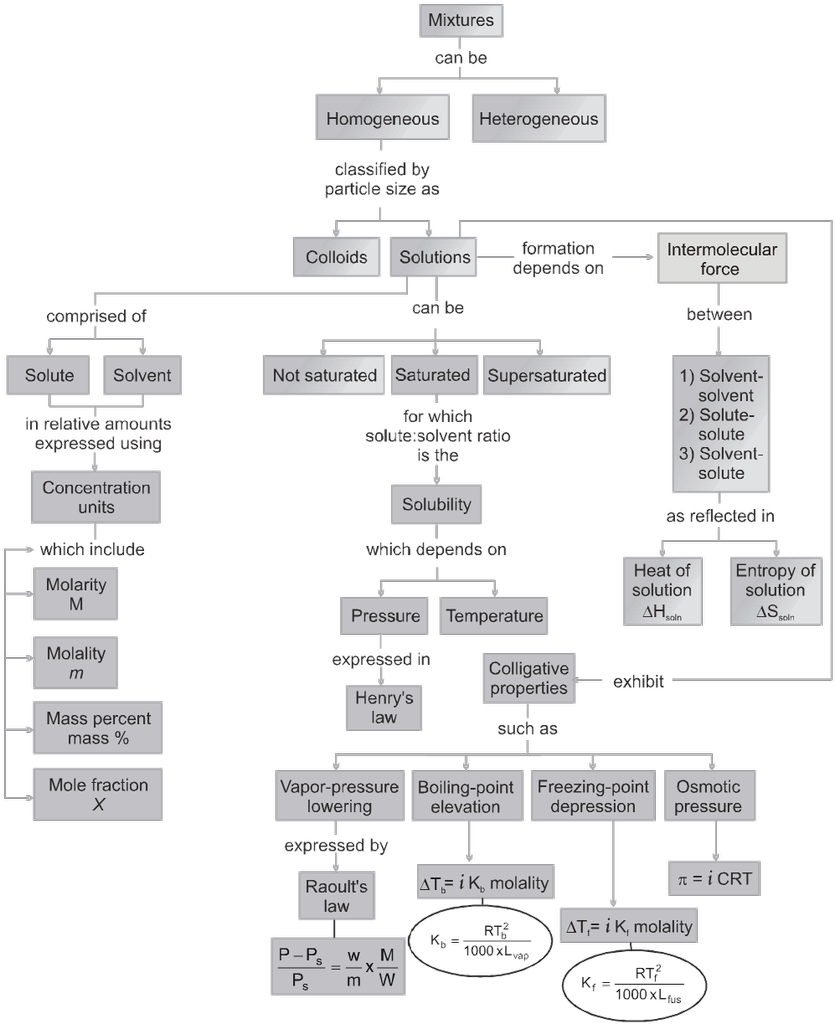
1. Types of solutions
- Books Name
- ACME SMART COACHING Chemistry Book
- Publication
- ACME SMART PUBLICATION
- Course
- CBSE Class 12
- Subject
- Chemistry
Chapter 2:
solutions
1.Introduction : A solution is a homogeneous mixture of two or more substances which are chemically non-reacting. We come across many types of solutions in our daily life. e.g., solid-liquid, liquid-liquid, gas-gas. In this chapter we will learn several properties of solutions and their applications.
Solution: A homogeneous mixture of two or more substances is known as solution
Solute: The substance present in smaller amount in a solution is called solute.
Solvent: The substance present in larger amount in a solution is called solvent.
Types of Solutions

The concentration of a solution can be expressed by different concentration terms which are described as follows.
1. Electrochemical cells
- Books Name
- ACME SMART COACHING Chemistry Book
- Publication
- ACME SMART PUBLICATION
- Course
- CBSE Class 12
- Subject
- Chemistry
Chapter 3
electrochemistry
Introduction
Batteries are everywhere in modern societies. They provide the electric current to start our autombiles and to power a host of products such as pocket caculators, digital watches, heart pacemaker, radio, and tape recorders.
Electrochemistry is the area of chemistry concerned with the interconversion of chemical and electrical.A battery is a an electrochemical cell, a device for interconverting chemical and electrical energy. A battery takes the energy relased by a spontaneous chemical reaction and uses it to produce electricity.
Electrochemical cell
It is device for converting chemical energy in to electrical energy.
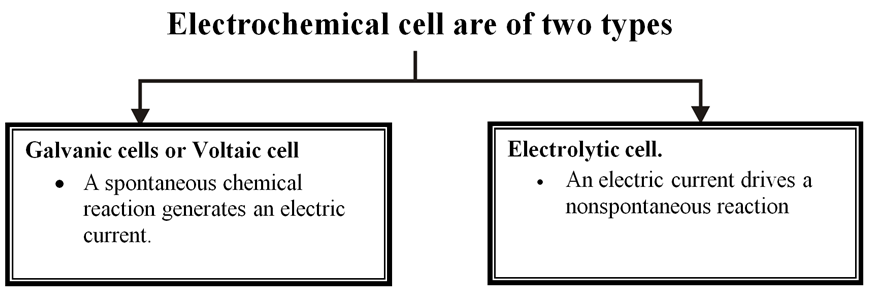
The two types of cells are therefore reverse of each other
Construction/ Working principle
When ever an metal strip is put in an electrolyte the process of oxidation and reduction takes place simultaneously within the system. Due to this there is a potential difference between the metal phase and the liquid phase.
On joining the metal strips through a wire (of negligible resistence) the current flows as long as the potential difference exists between the metal phase and the liquid phase.
I Anode :
Some metals (which are reactive) are found to have tendency to go into the solution phase when these are placed in contact with their ions or their salt solutions.
For example : Zn rod is placed in ZnSO4solution .
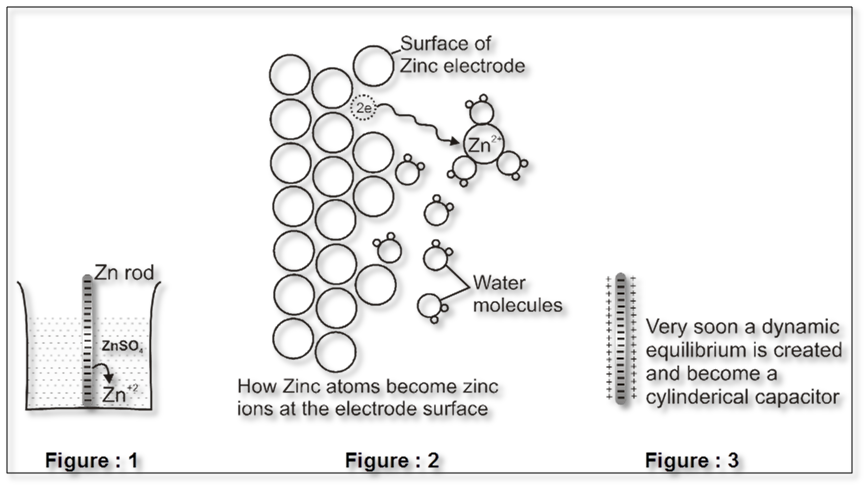
The Zn atom or metal atoms will move in the solution to form Zn+2. After some time following equilibrium will be established.
Zn(s) ![]() Zn2+ +2e–
Zn2+ +2e–
There will be accumulation of sufficient negative charge on the rod which will not allow extra zinc ions to move in the solution. i.e. solution will be saturated with Zn+2 ions.
The positive charge will be more concentrated nearly the rod.
The extra positive charge of the solution will be more concentrated around the negatively charged rod. An electrical double layer is developed in the system and hence a potential difference is created between the rod and the solution which is known as electrode potential
This particular electrode is known as anode :
- On anode oxidation will take place. (release of electron).
- To act as source of electrons.
- It is of negative polarity.
- The electrode potential is represented by EZn(s) / Zn2+ (aq)
II Cathode :
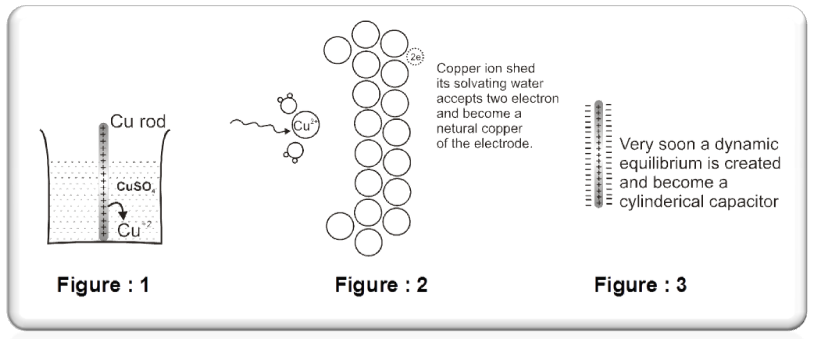
Some metals(Cu, Ag, Au etc.,) are found to have the opposite tendency i.e. when placed in contact with their aqueous ions, the ions from the solution will get deposited on the metal rod.
The following equilibrium will be established :
Cu2+ +2e– Cu(s).
So rod will have deficiency of electron (positive charge).Extra negative charge will surround this positively charged rod and form double layer. An electrical double layer is developed in the system and hence a potential difference is created between the rod and the solution which is known as electrode potential. This will be known as cathode.
- At cathode reduction will take place.(gain of e– will take place)
- To act as sink of electron.
- Positive polarity will be developed.
- Their electrode potential can be represented by : ECu2+(aq)/Cu(s)
Anode :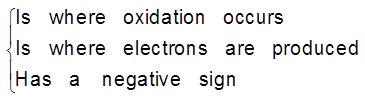
Cathode :
Construction of Cell :
It has two half–cells,each having a beaker containing a metal strip that dips in its aqueous solution.
The metal strips are called electrodes and are connected by an conducting wire.
Two solutions are connected by a salt bridge.
The oxidation and reduction half reactions occur at a separate electrodes and electric current flows through the wire.
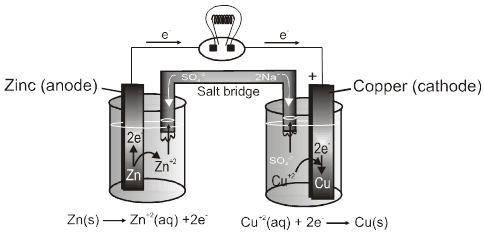
Selection of electrolyte for Salt Bridge :
The electrolyte in salt bridge should be such that speed of it's cation equals speed of it's anion in electrical field.
For that charge and sign of the ions should be almost equal.
Transport number of cation = Transport number of anion
or
Mobility of cation = Mobility of anion
KCl is generally preffered but KNO3 or NH4NO3 can also be used.
If Ag+, Hg2+, Pb2+, Tl+ ions are present in a cell then in salt bridge KCl is not used because there can be formation of precipitate of AgCl, Hg2Cl2, PbCl2 or TlCl at mouth of tube which will prevent the migration of ions and its functioning will stop.
Functions of Salt Bridge :
A salt bridge is a U–shaped inverted tube that contains a gel permeated with an inert electrolyte.
It connects the solution of two half cell to complete the circuit.
It minimise the liquid junction potential. The potential difference between the junction of two liquids.
It maintains the electhical neutrality of the solution in order to give continious flow or generation of current.
" The simultaneous electrical neutrality of the anodic oxidation chamber and cathodic reduction chamber is due to same mobility or velocity of K+ and NO3– ions taken into salt bridge.
If the salt bridge is removed then voltage drops to zero.
The ions of the inert electrolyte do not react with other ion in the solution and the ions are not oxidised or reduced at the electrodes.
Generally tube is filled with a paste of agar-agar powder with a natural electrolyte/generally not common to anionic/cathodic compartment with porous plugs at each mouth of tube.
It prevents mechanical mixing of two electrolytic solution.
Electrode Potential :
The driving force that pushes the negative charge electrons away from the anode and pulls them towards the cathode is an electrical potential called electromotive force also known as cell potential or the cell voltage. Its unit is volt
The potential difference devepoled between metal electrode and its ions in solution in known as electrode potential.
Electrode potential depends upon :
- Concentration of the solution.
- Nature of the metal.
- Nature of the electrolyte.
- Pressure temperature coditions.
The potential difference developed between metal electrodes and the solution of its ions at 1 M concentration at 1 bar pressure and 298 K is known as standard electrode potential.
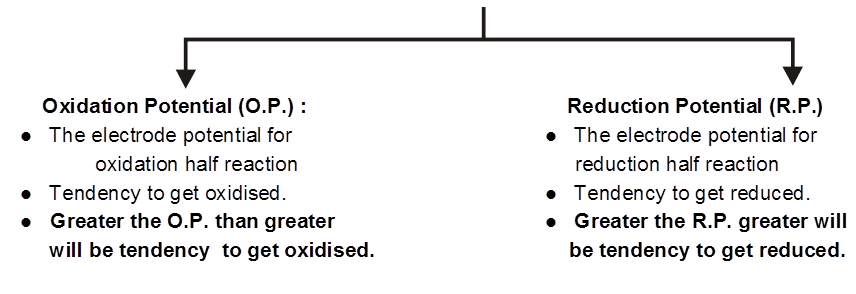
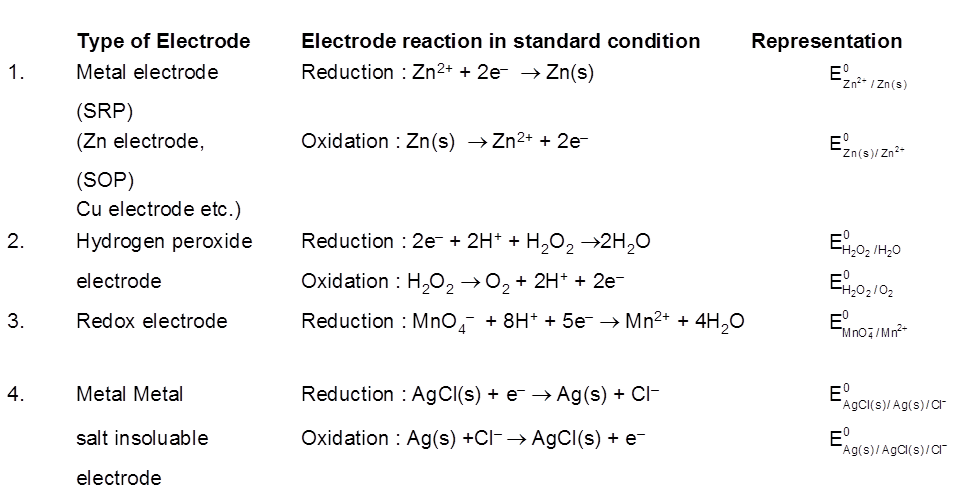
Reference electrode :
The potential of a singal electode cannot be determined what were the potential difference between two electrodes can be accurately measured using a reference electrode.
An electrode is chosen as a reference with respect to which all other electrodes are valued.
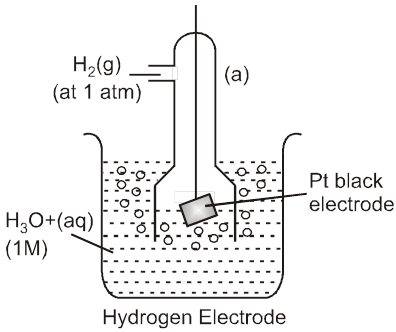
Standard Hydrogen Electrode (SHE) is taken as standard reference electrode. Its electrode potential is arbitrarily assumed to be 0.00 volt.
Standard Hydrogen Electrode (SHE) consists of a platinum electrode in contact with H2 gas and aqueous H+ ions at standard state conditions (1 atm H2 gas, 1 M H+ (aq), 25°C).
2H+ (aq, 1M) + 2e– → H2 (g, 1 atm) [E° = 0V]
H2(g, 1atm) → 2H+ (aq, 1M) + 2e– [E° = 0V]
Cell potential :
The difference in electrode potentials of the two half cell reactions (oxidation half cell and reduction half cell) is known as emf of the cell or cell potential.
The emf of the cell or cell potential can be calculated from the values of electrode potential of the two half cell constituning the cell. The following three methode are in use :
When oxidation potential of anode and reduction potential of cathode are taken into account :
E°cell = oxidation potential of anode + reduction potential of cathode
E°ox (anode) + E°red(cathode)
When reduction potential of both electrodes are taken into account :
E°cell = Reduction potential of cathode – Reduction potential of anode
= E°cathode – E°anode C both are reduction potential.
When oxidation potential of both electrodes are taken into account :
E°cell = oxidation potential of anode – Oxidation potential of cathode
= E°ox (anode) – E°ox (cathode)
The standard cell potential E° is the cell potential when both reactants and products are in their standard states – solutes at 1 M concentration, gases at a potential pressure of 1 atm, solids and liquids in pure from, with all at a specified temperature, usually 25° C.
E°cell is intensive property so on multiplying/Dividing cell reaction reaction by any number, the E°cell value would not change.
Free energy changes for cell reaction :
The free energy changeDG (a thermochemical quantity) and the cell potential E(an electrochemical quantity) both measure the driving force of a chemical reaction.
The values ofDG and E are directly proportional and are related by the equation.
DG = –nFE
where
n = Number of moles of electron transfered in the reaction.
F = Faraday constant = 96485 C/mole e– 96500 C/mole e–
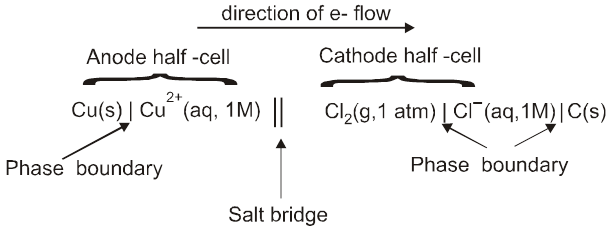
Shorthand Notation for Galvanic Cells
We require two half cells to produce an electrochemical cell, which can be represented by follwing few rules;
The anode half-cell is always written on the left followed on the right by cathode half cell.
The separation of two phases (state of matter) is shown by a vertical line.
The various materials present in the same phase are shown together using commas.
The salt bridge is represented by a double slash (||).
The significant features of the substance viz. pressure of a gas, concentration of ions etc. are indicated in brackets immediately after writing the substance.
For a gas electrode, the gas is indicated after the electrode for anode and before the electrode in case of cathode. (i.e Pt H2 / H+ or H+ /H2 Pt)

For SHE reference potential is taken to be zero at all temperature.
SOP = – SRP = 0 for SHE.
To calculate standard potential of any other electrode a cell is coupled with standard hydrogen electrode (SHE) and it's potential is measured that gives the value of electrode potential of that electrode.
Anode : Zinc electrode
Cathode : SHE
Cell : Zinc electrode || SHE
Cell potential :
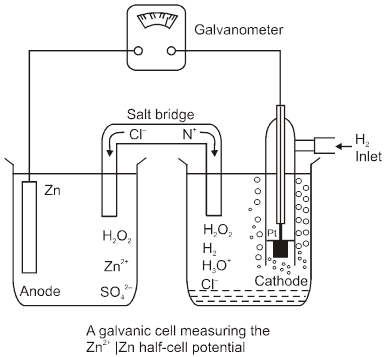
Ecell = ![]() – E°Zn2+/Zn
– E°Zn2+/Zn
= 0.76 V (at 298 K experimentaly)
So, E0Zn2+/Zn = – 0.76 V (SRP)
E0 Zn/Zn2+(aq) = 0.76 V(SOP)
So, w.r.t. H2, Zn has greater
tendency to get oxidised. In similar manner reduction potentials (SRP) at 298 K for many other electrodes are calculated and are arranged in a series increasing order known as electro chemical series.
Electrochemical Series :

Calculation of Electrode Potential of unknown electrode with the help of given (two) electrode.
Obtain the reaction of the 3rd electrode with the help of some algebraic operations on reactions of the given electrodes.
Then calculate DG of the 3rd reaction with the help of some algebaric operations of DG0 of 1st and 2nd reactions.
Use DG0 = –nF E0elec. to calculate unknown E.P.
![]() is intensive property so if we multiply/Devide electrode reaction by any number the
is intensive property so if we multiply/Devide electrode reaction by any number the ![]() value would not changed
value would not changed
i.e. Zn2+ + 2e– ® Zn(s) [E° = – 0.76 V[
Multiply by 2
2Zn2+ + 4e– ® 2Zn(s) [E° = – 0.76 V (remain same)]
1. Rate of a chemical reaction
- Books Name
- ACME SMART COACHING Chemistry Book
- Publication
- ACME SMART PUBLICATION
- Course
- CBSE Class 12
- Subject
- Chemistry
Chapter 4
chemical kinetics
Introduction :
In the thermodynamics, we have studied whether a reaction will take place or not and if it does then upto what extent (chemical equiibrium), In this chapter we will study about how fast a chemical reaction takes place and what are the different factors affecting this rate of chemical reaction. How to optimise the conditions as to maximse the output in optimum time. The last part of chapter will be dealing with the mechanism of a chemical reaction and catalysis.
Rate/Velocity of chemical reaction
The rate of change of concentration with time of different chemical species taking part in a chemical reaction is known as rate of reaction of that species.
Rate = ![]() =
= ![]() = mol lit–1 time–1 = mol dm–3 time–1
= mol lit–1 time–1 = mol dm–3 time–1
Rate is always defined in such a manner so that it is always a positive quantity.
Types of Rates of chemical reaction :
For a reaction R ![]() P
P
Average rate = ![]()
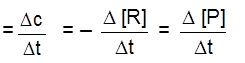
Instantaneous rate : rate of reaction at a particular instant.
Rinstantaneous 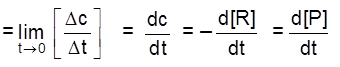
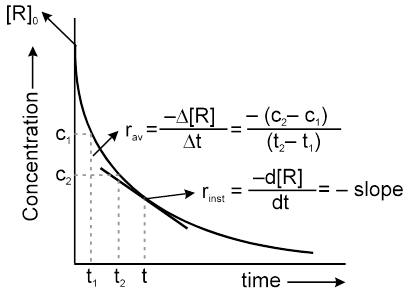
Instantaneous rate can be determined by drawing a tangent at time t on curve drawn for concentration versus time.
Initial Rate : Instantaneous rate at ‘t = 0’ is called initial rate [slope of tangent at t = 0].
Relation between reaction rates of different species involved in a reaction :
For the reaction : N2 + 3H2 ![]() 2NH3
2NH3
Rate of reaction of N2 = ![]()
Rate of reaction of H2 = ![]()
Rate of reaction of NH3 = ![]()
These rates are not all equal. Therefore by convention the rate of a reaction is defined as
Rate of reaction ![]()
Note : Rate of reaction value is dependent on the stoichiometric coefficients used in the reaction while rate of any species will be fixed value under given conditions.
2. Expressing concentration of solutions
- Books Name
- ACME SMART COACHING Chemistry Book
- Publication
- ACME SMART PUBLICATION
- Course
- CBSE Class 12
- Subject
- Chemistry
Expressing concentration of solutions
Concentration Terms :
% Concentration
Mass percentage. :It is the amount of solute in grams dissolved per 100 g of solution. e.g., 10% solution of sodium chloride means 10 g of solid sodium chloride present in 100 g of solution
% w/w = ![]() × 100
× 100
Ex. 10% w/w urea solution = 10 g of urea is present in 100 g of solution.
= 10 g of urea is present in 90 g of water.
Mass by volume percentage (% w/v) : It is defined as mass of solute dissolved per 100 ml of solution. It is commonly used in medicine and pharmacy.
% wt/vol. (w/v)
% w/v = wt. of solute/100 mL of solution
% w/v = 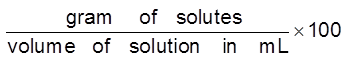
Ex.
10% (w/v) urea solution. = 10 g of urea is present in 100 mL of solution.
But not 10 g of urea present in 90 ml of water for dilute solution : volume solution = volume solvent.
Volume percentage (% v/v) : It is defined as volume of a solute dissolved per 100 ml of solution.
% v/v = ![]() × 100
× 100
Strength of solution in g/L : Weight of solute (in gram) per litre (1000 mL) of solution.
Ex.
10% (w/v) sucrose solution, then specify its concentration in g/L
100 mL .......... 10 g
1000 mL .......![]() = 100 g/L
= 100 g/L
Molarity (M) : It is expressed as the number of moles of solute per litre of solution.
Molarity = No. of moles of solute per litre of solution.
Let n = No. of moles of solute ; N = No. of moles of solvent ; V = volume of solution
![]()
no. of moles of solute = molarity x volume ( in L)
no. of m. moles of solute = molarity x volume ( in mL)
If V1 mL of C1 molarity solution is mixed with V2 mL of C2 molarity solution (same substance or solute)
Cf (V1+V2) = C1V1 + C2V2
Cf = 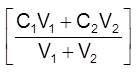 =
= ![]() where Cf = molarity of final solution
where Cf = molarity of final solution
Molality (m) : It is defined as number of moles of solute per 1000 g or 1 kg of solvent.
Molality = No. of moles of solute per kg(1000 g) of solvent.
Let w gram of solute (Molar mass = Mg/mole) is dissolved in 'W' gram of solvent.
molality = ![]() molality =
molality = ![]()
Molality not depends on temperature.
Normality : It is defined as number of gram equivalents of solute dissolved per litre of solution.
No. of equivalents per litre of solution = 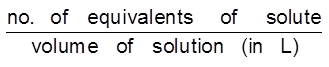 = n-factor molarity
= n-factor molarity
No. of equivalents = normality × volume (in L)
Equivalent mass = 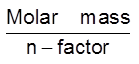
No. of equivalent=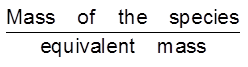 =
= 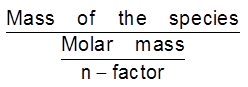
'n' - factor
(i) For oxidizing/reducing agents : no. of e– involved in oxidation/reduction half reaction per mole of oxidising agent /reducing agent.
e.g. : 5e– + 8H+ + MnO4– =Mn2+ + H2O n- factor = 5
(ii) For acid/ base reactions : no. of H+ ions displaced/ OH– ions displaced per mole of acid/ base.
e.g. : NaOH n - factor = 1 H2SO4 n - factor = 2
(iii) For salt : n = Total charge on cations.
or ![]()
total charge on anions
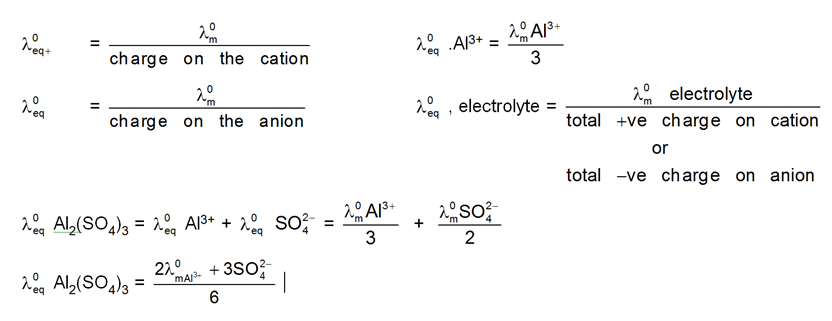
e.g. : Al2(SO4)3 n - factor = charge on the cation = 2 x 3 = 6
Mole-fraction (x) : It is the ratio of number of moles of a particular component to the total number of moles of all the components. e.g., mole-fraction of component A, xA = 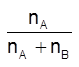 , where nA is the number of moles of component 'A' and nB is the number of moles of component 'B'.
, where nA is the number of moles of component 'A' and nB is the number of moles of component 'B'.
For binary mixture.
Xsolute = ![]() =
= ![]() ; XSolvent =
; XSolvent = ![]() =
= ![]()
Xsolute + XSolvent = 1
Parts per million (ppm) : The number of parts of solute present in 1 million parts of solution are called its ppm. When a solute is present in small quantities (very minute amounts), it is easier to express the concentration in parts per million.
(a) ppm (w/w) = 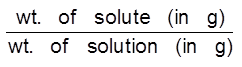 × 106
× 106
(b) ppm (w/v) = 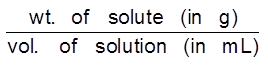 × 106
× 106
(c) ppm (moles/moles) = 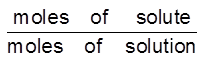 × 106
× 106
Table : 1

Note : All volume related concentration terms are temperature dependent.
3. Colligative properties & constitutional properties
- Books Name
- ACME SMART COACHING Chemistry Book
- Publication
- ACME SMART PUBLICATION
- Course
- CBSE Class 12
- Subject
- Chemistry
colligaive properties & constitutional properties
Constitutional Properties : Properties which are dependent on nature of particles are constitutional properties like electrical conductance.
Colligative properties : The properties of the solution which are dependent only on the total no. of particles relative to solvent/solution or total concentration of particles in the solution and are not dependent on the nature of particle i.e. shape, size, neutral /charge etc. of the particles.
There are 4 colligative properties of solution
Osmotic pressure
Relative lowering in vapour pressure
Elevation in b.p. (Tb)
Depression in freezing pt. (Tf)
(i) Osmosis & Osmotic pressure :
Osmosis: The spontaneous flow of solvent particles from solvent side to solution side or from solution of low concentration side to solution of high concentration side through a semipermeable membrane (SPM) is known as osmosis.
Ex.

Conclusion : After some time in (A) grape or egg will shrink and in (B) grape or egg will swell.
e.g. (i) A raw mango placed in concentrated salt solution loses water & shrivel into pickle.
(ii) People taking lot of salt, experience water retention in tissue cells. This results in puffiness or swelling called edema.
Biological Importance of Osmosis
The cell walls of plants and animals are semipermeable in nature and thus are responsible for the osmosis. When a cell comes in contact with water a tendency of flow of water into the cell is developed. The pressure developed inside the cell due to the inflow of water is called turgor.
If the cell comes in contact with a concentrated solution, cell would shrink, which is called plasmolysis. Cell walls are able to permit the flow of selected ions and molecules also along with water.
Various processes taking place due to osmosis are :
(a) Absorption of water from soil through the cell walls of roots.
(b) Movement of water from roots to the upper parts of plants & trees.
(c) Various types of locomotion in plants like stretching of leaves, opening of flowers, etc., are also based on osmosis.
(d) Germination is also caused due to osmosis as water moves into the seeds through cell walls.
The phenomenon of osmosis : A solution inside the bulb is separated from pure solvent in the beaker by a semipermeable membrane, Net passage of solvent from the beaker through the memberane occurs, and the liquid in the tube rises untill equilibrium is reached. At equilibrium, the osmotic pressure exerted by the column liquid in the tube is sufficient to prevent further net passage of solvent.
Although the passage of solvent through the membrane takes place in both direction, passage from the pure solvent side to the solution side is more favoured and occurs faster. As a result, the amount of liquid on the pure solvent side decreases, the amount of liquid on the solution side increases, and the concentration of the solution decreases.
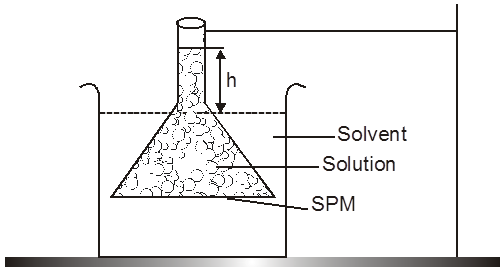
Osmotic Pressure : The equilibrium hydrostatic pressure developed by solution column when it is seperated from solvent by semipermeable membrane is called O.P. of the solution.
= gh ; = density of soln.
g = acceleration due to gravity ; h = eq. height
1 atm = 1.013 x 105 N/m2
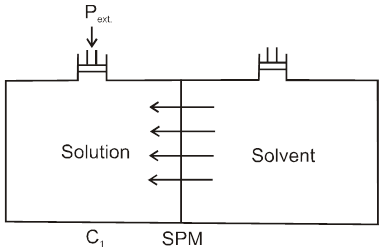
Definition : The external pressure which must be applied on solution side to stop the process of osmosis is called osmotic pressure of the solution.
If two solutions of concentration C1 and C2 are kept separated by SPM, and C1 > C2 then particle movement take place from lower to higher concentration. So, extra pressure is applied on higher concentration side to stop osmosis. And Pext. = (1 – 2)
Reverse Osmosis : If the pressure applied on the solution side is more than osmotic pressure of the solution then the solvent particles will move from solution to solvent side. This process is known as reverse osmosis.
Berkely : Hartely device/method uses the above pressure to measure osmotic pressure.
e.g. used in desalination of sea-water.
Vant – Hoff Formula (For calculation of osmotic pressure)
 concentration (molarity)
concentration (molarity)
 T
T
 = CST
= CST
S = ideal solution constant = atm.
= 8.314 J mol–1 K–1 (exp value)
= R (ideal gas) constant
= CRT =  RT (just like ideal gas equation)
RT (just like ideal gas equation)
In ideal solution solute particles can be assumed to be moving randomly without any interactions.
C = total concentration of all types of particles.
= C1 + C2 + C3 + s.................
= 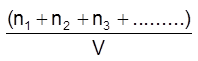
Type of solutions :
(a) Isotonic solution : Two solutions having same osmotic pressure are consider as isotonic solution.
1 = 2 (at same temperature)
(b) Hypotonic & Hypertonic solutions : If two solutions 1 and 2 are such that 2 > 1 , then 2 is called hypertonic solution and 1 is called hypotonic solution.
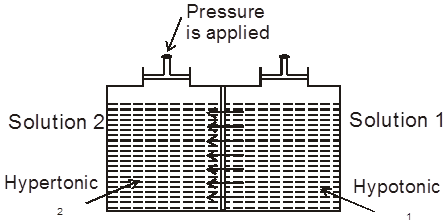
Conclusion :Pressure is applied on the hypertonic solution to stop the flow of solvent partices, this pressure become equal to (2 – 1) and if hypotonic solution is replaced by pure solvent then pressure becomes equal to 2.
4. Solution containing volatile solute / solvents
- Books Name
- ACME SMART COACHING Chemistry Book
- Publication
- ACME SMART PUBLICATION
- Course
- CBSE Class 12
- Subject
- Chemistry
Solution containing volatile solute / solvents
Mixture of 2 volatile liquids
Raoult's law ( for volatile Liq. Mixture )
Statement of Raoult's law ( for volatile liq. mixture ): In solution of volatile liquids, the partial vapour pressure of each component is directly proportional to its mole fraction.
pA µ xA => pA = xAPAº
pA = Partial vapour pressure of component A
xA = Mole fraction of component ‘A’ in solution.
PAº = Vapour pressure of pure component ‘A’ at given temperature
Derivation of total pressure over solution using Raoult’s law and Dalton’s law:
Let A, B be to two volatite liquids in a closed container as shown.
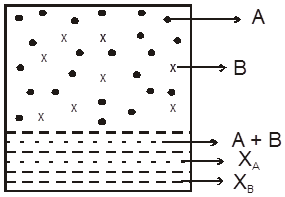
pA = xAPAº
Similarly, for liquid B we have,
pB = xBPBº
Total pressure over the solution PT , according to Dalton's law is
PT = pA + pB = xAPA0 + xBPB0
Determining composition of vapour phase:
Let,
yA = mole fraction of A in vapour phase above the solution and
yB = mole fraction of B in vapour phase above the solution
Now, we have, pA = yA PT .....Dalton's law of partial pressure for a gaseous mixture
pA = xAPAº ...........Raoult's law
Thus, pA = yA PT = xA PAº
Also, pB = yBPT = xBPBº
xA + xB = 1 = 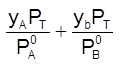 ; Thus
; Thus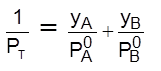
Graphical Representation of Raoult's Law:
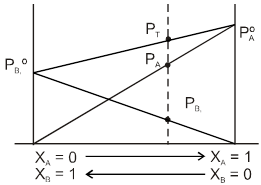
pA= xAPAº & pB = xB PBº
PT = xAPAº + xB PBº
PT = ( PAº – PBº ) xA + PB0
PT = ( PBº – PAº ) xB + PA0
This represents equation of straight line. PT v.s. x
Note: If PAº > PBº , A is more volatile than B. B.P. of A < B.P. of B.
Limitations of Raoult’s Law: Raoult's Law only works for ideal solutions. Very dilute solutions obey Raoult's Law to a reasonable approximation.
5. Ideal and non-ideal solutions
- Books Name
- ACME SMART COACHING Chemistry Book
- Publication
- ACME SMART PUBLICATION
- Course
- CBSE Class 12
- Subject
- Chemistry
Ideal and Non-ideal Solution
Ideal Solutions : Those solutions which obey Raoult's law over the entire range of conc. are called ideal solutions. When the forces of attraction between A—A, B—B is similar to A—B, then A and B will form ideal solution.
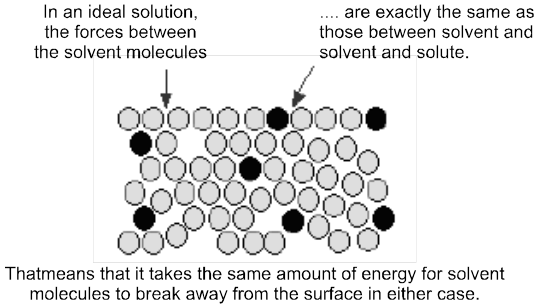
Properties of ideal solution :
(i) Raoult's law is obeyed
(ii) DHmix = 0, i.e., there should not be enthalpy change when components of ideal solutions are mixed.
(iii) DVmix = 0, (1L + 1L = 2L) i.e., there should not be change in volume on mixing. e.g.; n-hexane and n-heptane; ethyl bromide and ethyl iodide; benzene and toluene; chlorobenzene and bromobenzene form ideal solutions.
(iii) DSmix = +ve
(iv) DGmix = –ve
Non_Ideal Solutions :
Those solutions which do not obey Raoult's over the entire range of concentration are called non-ideal solutions.
When the forces of attraction between A—A, B—B is different from A—B then 'A' and 'B' form non-ideal solutions. For these solutions :
(i) Raoult's law is not obeyed.
(ii) DHmix ¹ 0 ;
(iii) DVmix ¹ 0.
Types of Non-Ideal Solutions : Non-ideal solution can be two types.
- Non ideal solutions showing positive deviation
- Non ideal solutions showing negative deviation
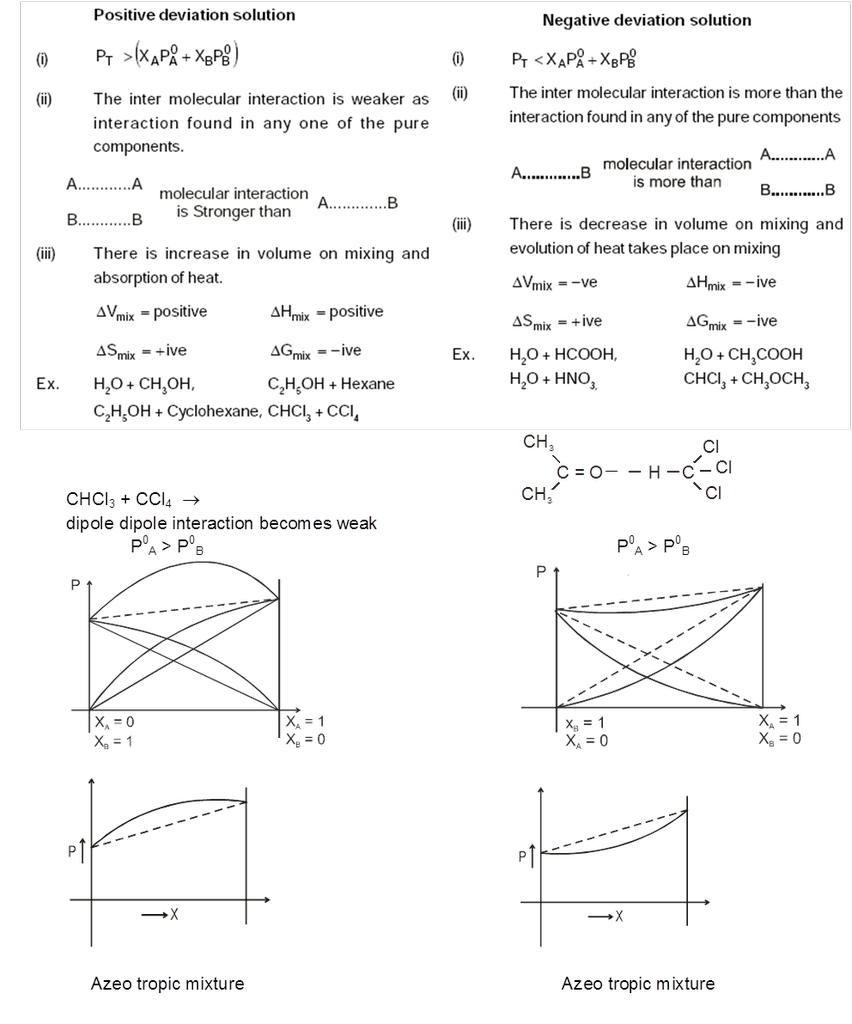
6. Azeotropic Mixtures
- Books Name
- ACME SMART COACHING Chemistry Book
- Publication
- ACME SMART PUBLICATION
- Course
- CBSE Class 12
- Subject
- Chemistry
Azeotropic Mixtures
Very large deviations from ideality lead to a special class of mixtures known as azeotropes, azeotropic mixtures, or constant-boiling mixtures.
Azeotropes : Liquid mixtures which distill over without changes in composition are called constant boiling mixtures or Azeotropes or Azeotropic mixtures.
A boiling liquid mixture at the azeotropic composition produces a vapour of exactly the same composition, and the liquid does not change its composition as it evaporates. Two types of azeotropes are known.
Minimum Boiling Azeotropes : Non-ideal solutions showing large positive deviation from Raoult's law form minimum boiling azeotropes which boil at temperature lower than boiling point of its components 'A' and 'B', e.g., water and benzene, chloroform and methanol.
Maximum Boiling Azeotropes : Non-ideal solutions showing large negative deviation from Raoult's law form maximum boiling azeotropes which boil at temperature higher than the boiling point of its components A and B respectively, e.g., a mixture of HCl and H2O containing 20.2% HCl by weight boils at 108.5ºC higher than either pure HCI (– 85°C) or water (100°C).
7. Solubility of gases in liquids
- Books Name
- ACME SMART COACHING Chemistry Book
- Publication
- ACME SMART PUBLICATION
- Course
- CBSE Class 12
- Subject
- Chemistry
Solubility of gases in liquids
Factors Affecting Solubility of Gas In Liquid :
(i) Nature of gas
(ii) Nature of liquid
(iii) Temperature
(iv) Pressure
Henry's Law (effect of pressure on solubility of gases in liquids) :
Statement : The solubility of a gas in a liquid at a given temperature is directly proportional to its partial pressure at which it is dissolved.
Let x = Mole fraction of unreacted gas in solution at a given temperature as a measure of its solubility.
p = Partial pressure of gas in equilibrium with the solution.
By Henry's law: x µ p or p µ x
That is; p = KHx or x = ![]() ,
,
where KH = Henry's law constant.
Characteristics of Henry's Law constant (KH).
(i) Unit same as those of pressure: torr or bar.
(ii) Different gases have different value of KH for the same solvent.
(iii) The KH value of a gas is different in different solvents and it increase with the increase in temperature.
(iv) Higher the value of KH of a gas, lower will be its solubility. Since, x = ![]() .
.
Plot of p Vs x is a straight line passing through the origin with slope equal to KH .
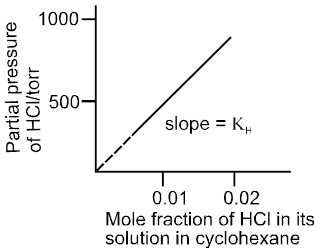
Plot of p Vs x for solution of HCl in cyclohexane.
Note : If a mixture of gases is brought in contact with solvent each constituent gas dissolves in proportion to its partial pressure. It means Henry's law applies to each gas independent of the pressure of other gas.
Effect of temperature : Solubility of gases in liquids decreases with rise in temperature.
Explanation : When dissolved, the gas molecules are present in liquid phase and the process of dissolution can be considered similar to condensation and heat is evolved in this process. We have learnt that dissolution process involves dynamic equilibrium and thus must follow Le Chatelier's principle. As dissolution of gases in liquids is an exothermic process, the solubility should decrease with increase of temperature.
Note : KH values for both N2 and O2 increase with increase of temperature indicating that the solubility of gases increases with decrease of temperature. It is due to this reason that aquatic spcies are more comfortable in cold water rather than warm water.
Applications of Henry's law : It has several applications in biological and industrial phenomena.
(i) To increase the solubility of CO2 in soft drinks and soda water the bottle is sealed under high pressure.
(ii) Scuba divers must cope with high concentrations of dissolved gases while breathing air at high pressure underwater. Increased pressure increases the solubility of atmosphere gases in blood. When the divers come towards surface, the pressure is gradually decreased. This releases the dissolved gases and leads to the formation of bubbles of nitrogen in the blood. This blocks capillaries and creates a medical condition known as bends, which are painful and dangerous to life. To avoid bends, as well as, the toxic effects of high concentrations of nitrogen in the blood, the tanks used by scuba divers are filled with air diluted with helium (11.7% helium, 56.2% nitrogen and 32.1% oxygen).
(iii) At high altitudes the partial pressure of oxygen is less than that at the ground level. This leads to low concentrations of oxygen in the blood and tissues of people living at high altitudes or climbers. Low blood oxygen causes climbers to become weak and unable to think clearly, symptoms of a condition known as anoxia.
Summary
2. Nernst equation
- Books Name
- ACME SMART COACHING Chemistry Book
- Publication
- ACME SMART PUBLICATION
- Course
- CBSE Class 12
- Subject
- Chemistry
Nernst Equation
Cell potentials depend on temperature and on the composition of the reaction mixtures.
It depends upon the concentration of the solute and the partial pressure of the gas, if any.
The dependence upon the concentration can be derived from thermodynamics.
From thermodynamics
DG = DG° + RT ln Q
– nFE = – nFE° + 2.303 R T log Q
E = E° – ![]() log Q
log Q
Take
T = 298 K ,
R = 8.314 J/mol K ,
F = 96500 C
Now we get,
E = E° – ![]() log Q
log Q
Where
n = number of transfered electron ,
Q = reaction quotient
Nernst equation can be used to calculate cell potentials for non standard conditions also.
Nernst equations can be applied to half cell reactions also.
Applications of Nerst equation
Nernst Equation for Electrode Potential
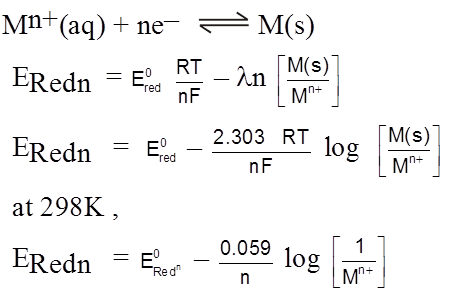
Hydrogen Electrode
H2(g) ![]() 2H+(aq) + 2e–
2H+(aq) + 2e–
E = E0 –![]() log
log 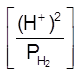
Metal–metal soluble salt electrode.
Zn2+ + 2e–  Zn(s)
Zn(s)
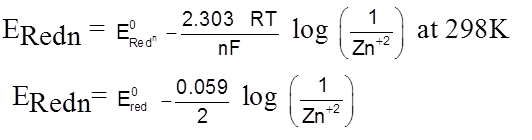
Gas – electrode Hydrogen electrode.
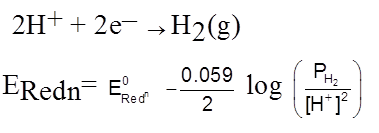
Redox electrode
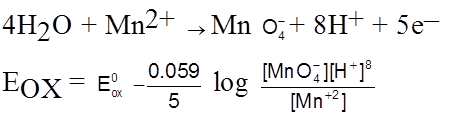
Nernst Equation for cell Potential :
aA + bB ![]() CC + dD
CC + dD
Ecell = ![]() –
– ![]() lnQ
lnQ
n – no. of electrons which gets cancelled out while making cell reaction.
Equilibrium in electrochemical cell
G0 = – nF Eºcell
G = – nF Ecell
From thermo dynamics
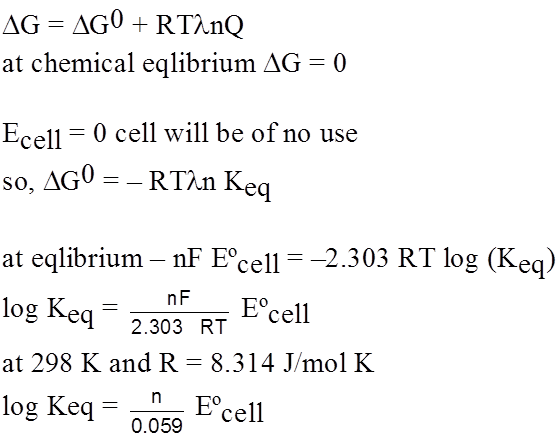
Concentration cells :
A concentration cell consists of two electrodes of the same material, each electrode dipping in a solution of its own ions and the solution being at different concentrations.
The two solutions are separated by a salt bridge.
e.g. Ag(s) | Ag+ (a1) || Ag+ (a2) | Ag(s) (a1 < a2) a1 , a2 are concentrations of each half cell
At LHS electrode Anode : Ag (s) ![]() Ag+(a1) + e–
Ag+(a1) + e–
At RHS electrode Cathode : Ag+(a2) + e– ![]() Ag(s)
Ag(s)
The net cell reaction is : Ag+ (a2) ![]() Ag+ (a1)
Ag+ (a1)
The nernst eq. is
Ecell = – ![]() log
log ![]() (Here n = 1, Temp, 298 K)
(Here n = 1, Temp, 298 K)
Likewise, the e.m.f. of the cell consisting of two hydrogen electrodes operating at different pressure P1 and P2 (P1 > P2 ) and dipping into a solution HCl is :
Ecell = ![]() log
log ![]() (at 298 K)
(at 298 K)
Solubility product and EMF (Metal Metal Insoluble Salt Electrode) :
A half cell containing metal M and its sparingly soluble salt MA in a saturated solution.
i.e M(s) | MA (satd) or a metal, its sparingly soluble salt in contact with a solution of a soluble salt NaA of the same anion, i.e. M(s) | MA(s) | NaA is set up.
The solubility product of a sparingly doubles salt is a kind of equilibrium constant.
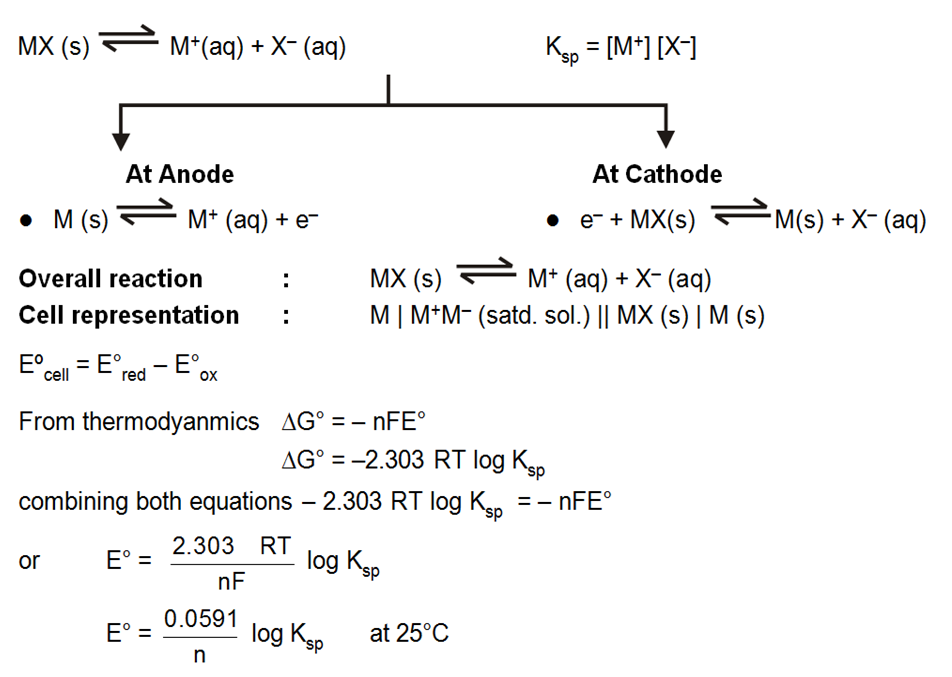
Work done by a cell :
(i) Let 'n' faraday charge be taken out of a cell of EMF 'E' ; then work done by the cell will be calculated as : work = Charge × Potential = nFE
(ii) Work done by cell = Decrease in free energy
so –DG = nFE
or Wmax = + nFEº where Eº is standard EMF of the cell
3. Conductance of electrolytic solutions
- Books Name
- ACME SMART COACHING Chemistry Book
- Publication
- ACME SMART PUBLICATION
- Course
- CBSE Class 12
- Subject
- Chemistry
Conductance of electrolytic solutions
Electrolytic Conductance :

Factors Affecting Conductance & Resistance :
1. Solute – Solute interactions (Inter – Ionic force of attraction) Greater the force of attraction, greater will be the resistance.
Force ![]() Charge
Charge
2.Solute – Solvent Interaction (Hydration/Solvation of Ions) Greater the solvation
Solvation ![]() Charge
Charge ![]() greater will be resistance Li+ (Hydrated largest) Cs+ (Hydrated smallest)
greater will be resistance Li+ (Hydrated largest) Cs+ (Hydrated smallest)
resistance of LiCl > resistance of CsCl
3. Solvent solvent interaction (Viscosity) : greater the viscosity greater will be resistance
4. Temperature
T ![]() R
R ![]()
5. Nature of electrolyte
Weak electrolyte – high resistance strong electrolyte – Low resistance
Resistance :
R = ![]() (Ohm's law (
(Ohm's law ( ![]() )
)
R = ![]()
![]() – resistivity/specific resistance
– resistivity/specific resistance
– resistance of unit length wire of unit area of cross section = constant = (![]() m)
m)
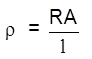
Resistivity of a solution is defined as the resistance of the solution between two electrodes of 1 cm2 area of cross section and 1 cm apart.
or
Resistance of 1 cm3 of solution will be it's resistivity.
Conductance :

= S (Siemens)
Conductivity/specific conductance
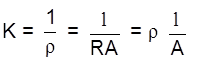
unit –1 cm–1
= conductivity of 1 cm3 of solution
a concentration of ions
K = ![]() G =
G = ![]()
K ![]() ( no. of ions) no. of charge carries
( no. of ions) no. of charge carries
Since conductivity or resistivity of the solution is dependent on it's concentration, so two more type of conductivities are defined for the solution.
Molar conductivity/molar conductance ((lm) :
Conductance of a solution containing 1 mole of an electrolyte between 2 electrodes which are 1cm apart.
Let the molarity of the solution 'C'
C moles of electrolyte are present in 1 Lt. of solution.
so molar conductance = K
![]()
Its units are Ohm–1 cm2 mol–1
Equivalent conductance : Conductivity of a solution containing 1 g equivalent of the electrolyte.
leq – equivalent conductivity/conduction.
leq = 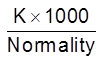
Its units are Ohm–1 cm2 eq–1
Variation of conductivity and molar conductivity with concentration
Conductivity always decreases with the decrease in concentration both for weak and strong electrolytes.
The number of ions per unit volume that carry the current in a solution decreases on dilution.
Molar conductivity increases with decreases in concentration. This is because the total volume, V of solution containing one mole of electrolyte also increases.
Molar conductivity is the conductance of solution.
When concentration approaches zero, the molar conductivity is known as limiting molar conductivity and is represented by the symbol ![]() .
.
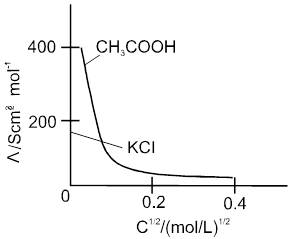
Strong Electrolytes :
For strong electrolytes. ![]() increses slowly with dilution and can be represented by the equation
increses slowly with dilution and can be represented by the equation
![]()
The value of the constant 'A' for a given slovent and temperature depends on the type of electrolyte i.e. the charges on the cations and anion produced on the dissociation of the electrolyte in the solution.
Example : Thus NaCl, CaCl2, MgSO4 are known as 1-1 , 2-1 and 2-2 electrolyte respectively.
All electrolytes of a particular type have the same value for 'A'.
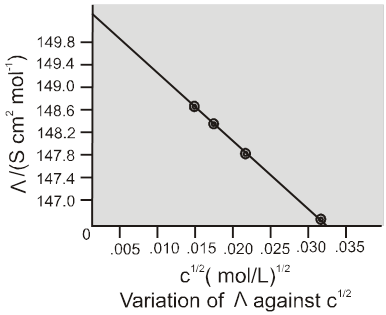
Weak electrolytes
Weak electrolytes like acetic acid have lower degree of dissociation at higher concentration and hence for such electrolytes, the change in  with dilution is due to increases in the number of ions in total volume of solution that contains 1 mol of electrolyte.
with dilution is due to increases in the number of ions in total volume of solution that contains 1 mol of electrolyte.
At infinite dilution (i.e. concentration c ![]() zero) electrolyte dissociates completely (a= 1),but at such low concentration the conductivity of the solution is so low that it connot be measured accurately.
zero) electrolyte dissociates completely (a= 1),but at such low concentration the conductivity of the solution is so low that it connot be measured accurately.
Molar conductivity versus c1/2 for acetic acid (weak electrolyte) and potassium chloride
(strong electrolyte in aqueous solutions.
Kohlarausch's Law :
"At infinite dilution, when dissociation is complete, each ion makes a definite contribution towards equivalent conductance of the electrolyte irrespective of the nature of the ion with which it is associated and the value of equivalent conductance at infinite dilution for any electrolyte is the sum of contribution of its constituent ions."
i.e., l¥ = l+ + l–
At infinite dilution or near zero concentration when dissociation is 100%, each ion makes a definite contribution towards molar conductivity of electrolyte irrespective of the nature of the other ion. (because interionic forces of attraction are zero)
![]()
V+= no. of cation in one formula unit of electrolyte, = no. of anions in one formula unit of electrolyte
For NaCl = 1 v- = 1
For Al2(SO4)3 = 2 v- = 3
![]()
Applications of Kohlaraushch's law
Calculate ![]() for any electrolyte from the
for any electrolyte from the ![]() of individual ions.
of individual ions.
etermine the value of its dissociation constant once we known the ![]() and
and ![]() at a given concentration c.
at a given concentration c.
Degree of dissociation : At greater dilution the ionization become 100%, therefore called infinite dilution.
At lower dilution the ionization (dissociation into ions) is less than 100% and equivalent conductance become lower,
i.e., leq < l°eq
degree of dissociation
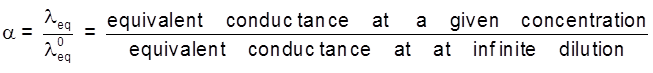
Dissociation constant of weak electrolyte :
KC = ![]()
a = degree of dissociation
C = concentration
The degree of dissociation then it can be approximated to the ratio of molar conductivity ![]() at the concentration c to limiting molar conductivity,
at the concentration c to limiting molar conductivity, ![]() , Thus we have :
, Thus we have :
![]()
But we known that for a weak electrolyte like acetic acid.
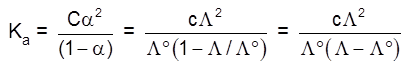
Solubility(s) and KSP of any sparingly soluble salt.
Sparingly soluble salt = Very small solubility
Solubility = molarity = 0
so, solution can be considered to be of zero conc or infinite dilution.
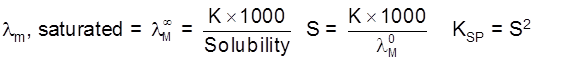
Variation of K, lm & leq of solutions with Dilution
Kconc. of ions in the solution. In case of both strong and weak electrolytes on dilution the concentration of ions will decrease hence K will decrease.

4. Electrolytic cells and electrolysis
- Books Name
- ACME SMART COACHING Chemistry Book
- Publication
- ACME SMART PUBLICATION
- Course
- CBSE Class 12
- Subject
- Chemistry
Electrolytic cells and electrolysis
Electrolysis :
Electrolyte is a combination of cations and anions which in fused state can conduct electricity.
This is possible due to the movement of ions from which it is made of and electrolyte.
The process of using an electric current to bring about chemical change is called electrolysis.
Electrolysis is a process of oxidation and readuction due to current in the electrolyte.
The product obtained during electrolysis depends on following factors.
The nature of the electrolyte
The concentration of electrolyte
The charge density flowing during electrolysis.
The nature of the electrode
Active vs Inactive electrodes :
The electrodes in the cell that are active because the metals themselves are components of the half reactions.
As the cell operates, the mass of the zinc electrode gradually decreases, and the [Zn2+] in the anode half – cell increases. At the same time, the mass of the copper electrode increases and the [Cu2+] in the cathode half – cell decreases; we say that the Cu2+ "plates out" on the electrode.
For many redox reactions, however, there are no reactants or products capable of serving as electrodes. Inactive electrodes are used, most commonly rods of graphite or platinum, materials that conduct electrons into or out of the cell but cannot take part in the half -reactions.
In a voltaic cell based on the following half reactions, for instance, the species cannot act as electrodes
2I–(aq) ![]() I2(s) +2e– [anode ; oxidation]
I2(s) +2e– [anode ; oxidation]
MnO4– (aq) + 8H+ (aq) + 5e– ![]() Mn2+ (aq) + 4H2O(λ) [cathode ; reduction]
Mn2+ (aq) + 4H2O(λ) [cathode ; reduction]
Therefore, each half – cell consists of inactive electrodes immersed in an electrolyte solution that contains all the species involved in that half -reaction. In the anode half-cell, I– ions are oxidized to solid I2. The electrons released flow into the graphite anode, through the wire, and into the graphite cathode. From there, the electrons are consumed by MnO4– ions as they are reduced to Mn2+ ions.
Examples of Electrolysis
Using inert (pt/graphite) electrodes.
Cathode (red) : Pb2+ + 2e– ![]() Pb(s) E0 = 0.126V
Pb(s) E0 = 0.126V
Anode : 2Br- ![]() Br2 + 2e- E0 = – 1.08 V
Br2 + 2e- E0 = – 1.08 V
Ecell = – 0.126 – (0.108) x 10 = – 1.206 V
Eext > 1.206 V
Electrolysis of CuSO4 molten
Cathode : Cu2+ + 2e– ![]() Cu [E0 = +0.34 V]
Cu [E0 = +0.34 V]
Anode : ![]() [E0 = – 2.05 V]
[E0 = – 2.05 V]
H2S2O8 – marchall's acid peroxy disulphuric acid.
Ecell = 0.34 – (2.05) = – 1.71 V (negative not feasible)
Electrolysis of aq CuSO4
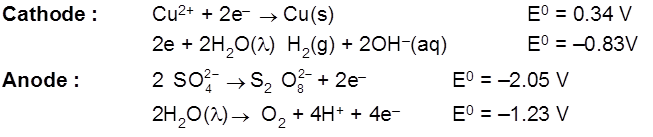
Electrolysis of aq NaBr solution (initially PH = 7)
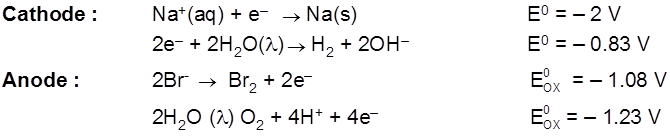
Electrolysis of aq NaCl
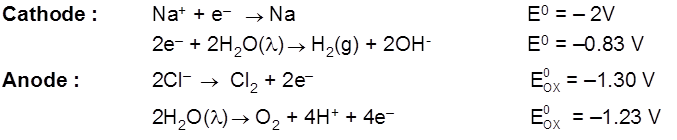
Rate of production of Cl2 is more than rate of production of O2 gas.
Note : According to thermodynamics, oxidation of H2O to produce O2 should take place on anode but experimentally (experiment from chemical kinetics) the rate of oxidation of water is found to be very slow. To increase it's rate, the greater potential difference is applied called over voltage or over potential but because of this oxidation of Cl– ions also become feasible and this takes place on anode.

Electrolysis using attackable (reactive) electrodes.
- Electrolysis of aq. CuSO4 using Cu electrode.
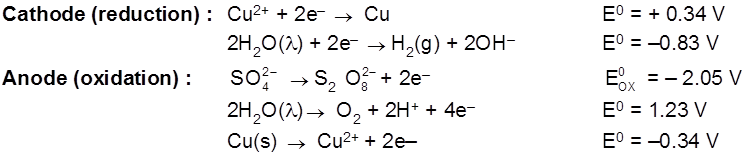
electrolytic refining
- AgNO3(aq) using Cu cathode & Ag anode.
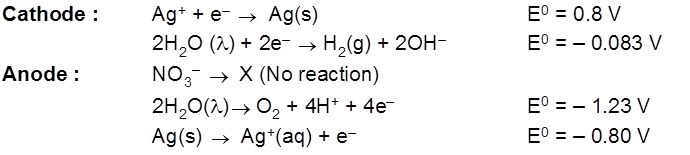
Faraday's Law of Electrolysis :
1st Law : The mass deposited/released/produced of any substance during electrolysis is proportional to the amount of charge passed into the electrolyte.
WQ
W = ZQ
Z – electrochemical equivalent of the substance.
Unit of Z =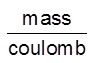 = Kg/C or g/C
= Kg/C or g/C
Z = Mass deposited when 1 C of charge is passsed into the solution.
Equivalent mass (E) : mass of any substance produced when 1 mole of e– are passed through the solution during electrolysis.
E = 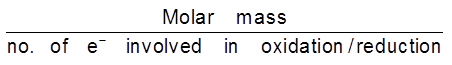
e.g.
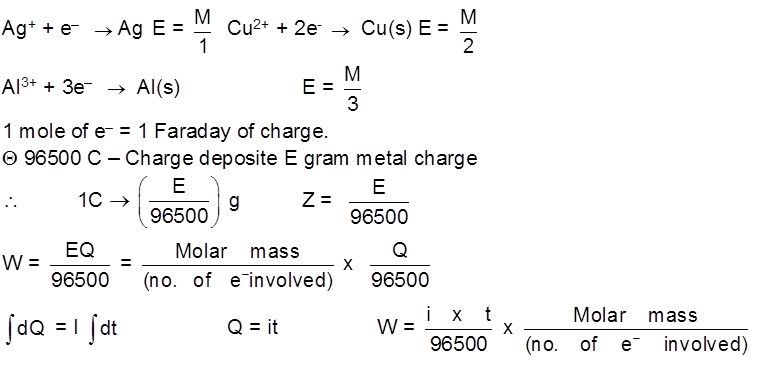
2nd Law : When equal charge is passed through 2 electrolytic cells and this cells are connected in series then mass deposited at electrode will be in the ratio of their electrochemical equivalents or in the ratio of their equivalent masses. 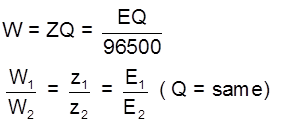
Current Efficiency :
current efficiency = ![]() x 100
x 100
current efficiency = 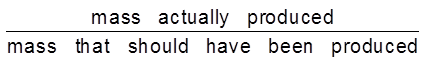 x 100
x 100
5. Batteries
- Books Name
- ACME SMART COACHING Chemistry Book
- Publication
- ACME SMART PUBLICATION
- Course
- CBSE Class 12
- Subject
- Chemistry
Batteries
Battery :
A battery is a an electrochemical cell, a device for interconverting chemical and electrical energy. A battery takes the energy relased by a spontaneous chemical reaction and uses it to produce electricity.
Primary Batteries : In the primary batteries, the reaction occurs only once and after use over a period of time battery becomes dead and cannot be reused again. The most familiar example of this type is the dry cell (known as Leclanche cell after its discoverer) which is used commonly in our transistors and clocks. All substances used are either pure solids or pure liquids.
Types of primary batteries :
(i) Dry cell %
Anode : Zn(s)
Cathode : MnO2(s)
Electrolyte : Paste of NH4Cl + ZnCl2 in starch
Cathode :
MnO2 + NH4+ + e– ![]() MnO(OH) + NH3
MnO(OH) + NH3
(Oxidation state of Mn changes from +4 to +3)
Anode :
Zn ![]() Zn2+ + 2e–
Zn2+ + 2e–
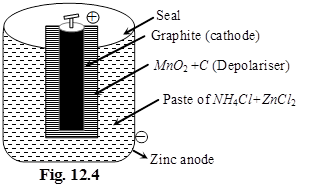
(ii) Mercury cell :
Anode: HgO(s)
Cathode : Zn(Hg)
Electrolyte : Paste of KOH + ZnO
Cathode :
Zn(Hg) + 2OH– ![]() ZnO(s) + H2O(l) + 2e–
ZnO(s) + H2O(l) + 2e–
(amalgam)
Anode :
HgO(s) + H2O(l) + 2e– ![]() Hg(l) + 2OH–
Hg(l) + 2OH–
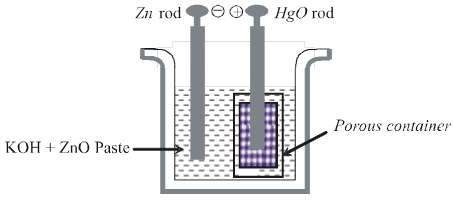
Secondary Batteries : A secondary cell afer use can be recharged by passing current through it in the opposite direction so that it can be used again. A good secondary cell can udnergo a large number of discharing and charging cycles. The most important secondary cell is the lead storage battery commonly used in automobiles and inverters.
Anode : Pb(s)
Cathode : PbO2(s)
Electrolyte : 38 % Conc. H2SO4 solution Ecell = 2.05 V.

During the working of the cell discharge H2SO4 will be consumed so it's concentration in the solution hence density of the solution will decrease during charging of the cell PbSO4 will get converted into Pb(s) and, PbO2(s) and H2SO4 will be produced.
Nickel – cadmium battery.
Ecell = constant as cell reaction has pure solide/liquids only.
Anode : Cd(s)
Cathode : NiO2(s)
Electrolyte : KOH
Cd + 2OH– ![]() Cd(OH)2 + 2e–
Cd(OH)2 + 2e–
2e– + NiO2 + 2H2O ![]() Ni(OH)2(s) + 2OH–
Ni(OH)2(s) + 2OH–
Cd(s) + NiO2(s) + 2H2O(λ)![]() Cd(OH)2(s) + Ni(OH)2(s)
Cd(OH)2(s) + Ni(OH)2(s)
6. Fuel cells
- Books Name
- ACME SMART COACHING Chemistry Book
- Publication
- ACME SMART PUBLICATION
- Course
- CBSE Class 12
- Subject
- Chemistry
Fuel cell
Fuel cells (H2 – O2 cell) : Galvanic cells those are designed to convert the energy of combustion of fuels like hydrogen, methane, methanol etc. directly into electrical energy are called fuel cells.
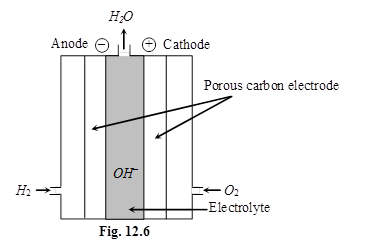
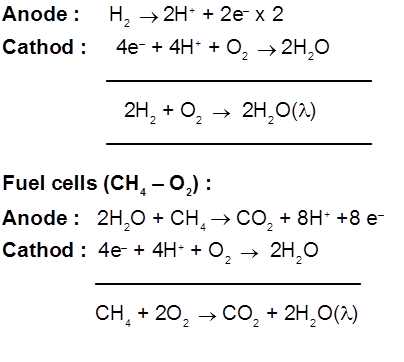
7. Corrosion
- Books Name
- ACME SMART COACHING Chemistry Book
- Publication
- ACME SMART PUBLICATION
- Course
- CBSE Class 12
- Subject
- Chemistry
Corrosion
It is a process of deterioration of a metal as a result of its reaction with air or water (environment) surrounding it.
In case of iron, corrosion is called rusting. Chemically, rust is hydrated form of ferric oxide, Fe2O3 .xH2O Rusting of iron is generally caused by moisture, carbon dioxide and oxygen present in air.
Mechanism of corrosion :
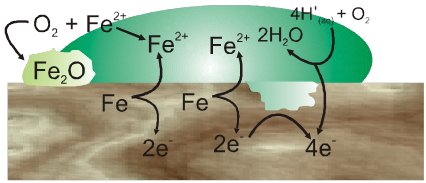
Oxidation :
Fe(s) ![]() Fe2+ (aq) + 2e–
Fe2+ (aq) + 2e–
Reduction :
2O2–(g) + 4H+ (aq) ![]() 2H2O(I)
2H2O(I)
Atomospheric oxidation :
2Fe2+(aq) + 2H2O(l) + 1/2O2 ![]() Fe2O3(s) + 4H+(aq)
Fe2O3(s) + 4H+(aq)
Factors which affect corrosion : The main factors which affect corrosion are
Rate of corrosion µ Rectivity of metal
µ Presence of impurities.
µ Presence of electrolytes.
µ temperature (with in a reason able limit)
Corrosion protection : Corrosion of metals can be prevented in many ways. Some commonly used methods are
(i) By surface coating
(a) By applying, oil, grease, paint or varnish on the surface.
(b) By sacrifical protection; coating/depositing a thin layer of any other metal which does not corrode. For example, iron surface can be protected from corrosion by depositing a thin layer of zinc, nickel or chromium on it.
(c) By Galvanization : Prevention of corrosion of iron by Zn coating.
(ii) cathodic protection : (By connecting metal to a more electropositive metal) In presence of the more electropositive metal, the given metal does not get corroded. For example, iron can be protected from corrosion by connecting it to a block/plate of zinc or magnesium.
(iii) By forming insoluble phosphate or chromate coating : Metal surfaces are treated with phosphoric acid to form an insoluble phosphate. Formation of a thin chromate layer also prevents the corrosion of metals.
(iv) Using anti – rust solutions : Solutions of alkaline phosphates and alkaline chromates are generally used as anti – rust solutions.
2. Factors influencing rate of a reaction
- Books Name
- ACME SMART COACHING Chemistry Book
- Publication
- ACME SMART PUBLICATION
- Course
- CBSE Class 12
- Subject
- Chemistry
Factors affecting rate of chemical reaction :
1. Concentration
2. Temperature
3. Nature of reactants & products
4. Catalyst
5. pH of the solution
6. Dielectric constant of the medium.
7. Radiations/light
8. Pressure
9. Electrical & Magnetic field.
The first four factors generally affect rate of almost all reactions while other factors are specific to some reactions only. The common examples of these reactions are :
Concentration : We known from law of mass action that Rate is proportional to concentration of reactants. “ So, generally rate of reaction decreases with passage of time, since concentration of reactants decreases.
Temperature :
Nature of reactants & Products :
(a) Physical state of reactants :
Gaseous state > Liquid state > Solid state
Decreasing order of rate of reaction.
(b) Physical size of reactants : As we decreases the particle size rate of reaction increases since surface area increases.
(c) Chemical nature of reactants :
If more bonds are to be broken, the rate of reaction will be slow.
Similarly bond strength is more, rate of reaction will be slow.
Catalyst :
Presence of positive catalyst lower down the activation energy hence increases the rate of reaction.
presence of negative catalyst increases activation energy hence decreases the rate of reaction.
Radiations/light : Radiation are useful for photochemical reaction.
Pressure : Pressure is important factor for gaseous reaction.
Rate Law (Dependence of rate on concentration of reactants) :
The representation of rate of reaction in terms of the concentration of the reactants is called the rate law.
It can only be established by experiments.
Generally rate law expressions are not simple and these may differ for the same reaction on conditions under which the reaction is being carried out.
But for large number of reactions starting with pure reactants we can obtain simple rate laws.
For these reactions :
Rate µ (conc.)order
Rate = K (conc.)order – differential rate equation or rate expression
Where K = Rate constant = specific reaction rate = rate of reaction when concentration is unity
unit of K = (conc)1– order time–1
Note : Value of K is a constant for a given reaction, depends only on temperature
Order of reaction :
Let there be a reaction m1A + m2B ¾® products.
Now, if on the basis of experiment, we find that
R µ [A]P [B]q Where p may or may not be equal to m1 & similarly q may or may not be equal to m2.
p is order of reaction with respect to reactant A and q is order of reaction with respect to reactant B and (p + q) is overall order of the reaction.
Note : Order of a reaction can be ‘zero’ or any whole number, can be a fractional number and it can even be negative with respect to a particular reactant. But oveall order is not found to be negative for any reaction till observed.
Examples showing different values of order of reactions :

The reaction (2) does not take place in one single step. It is almost impossible for all the 12 molecules of the reactants to be in a state of encounter simultaneously. Such a reaction is called complex reaction and takes places in a sequence of a number of elementary reactions. For an elementary reaction the sum of stoichiometric coefficients = order of the reactions. But for complex reactions order is to be experimentally calculated.
3. Integrated rate equations
- Books Name
- ACME SMART COACHING Chemistry Book
- Publication
- ACME SMART PUBLICATION
- Course
- CBSE Class 12
- Subject
- Chemistry
Integrated rate laws
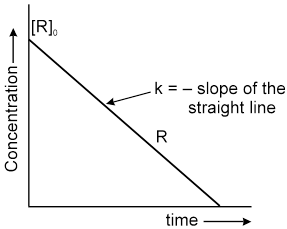
(a) Zero Order Reactions :
For a zero order reaction
General rate law is, Rate = k [conc.]º = constant
If C0 is the initial concentration of a reactant and Ct is the
concentration at time ‘t’ then
Rate = k = ![]() or kt = C0 – Ct or Ct = C0 – kt
or kt = C0 – Ct or Ct = C0 – kt
Unit of K = same as that of Rate = mol lit–1 sec–1.
Time for completion =![]()
t1/2 (half life period) at t1/2 , Ct =![]() , so kt1/2 =
, so kt1/2 = ![]() Þ t1/2 =
Þ t1/2 = ![]()
t1/2 µ C0
Examples of zero order reactions :
Generally decomposition of gases on metal surfaces at high concentrations follow zero order kinetics.
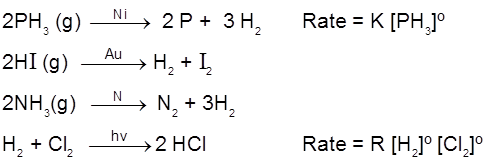
(b) First Order Reactions :
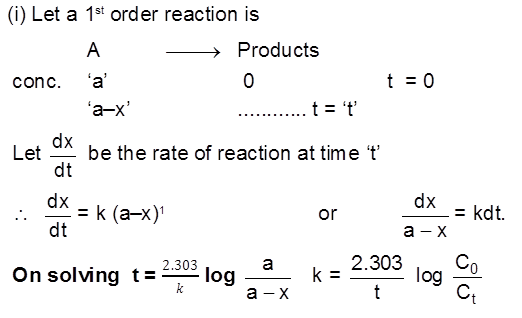
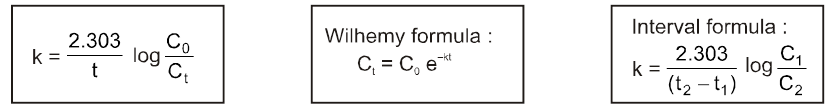
If any substance is growing/increasing following first order kinetics then :
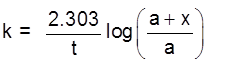
where a is initial concentration of the substance and x is the increment in its concentration after time t.
Half life time (t1/2)
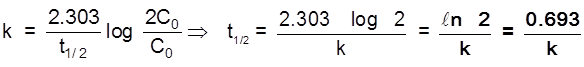
Half life period for a 1st order reaction is a constant quantity.
Graphical Representation :
![]()
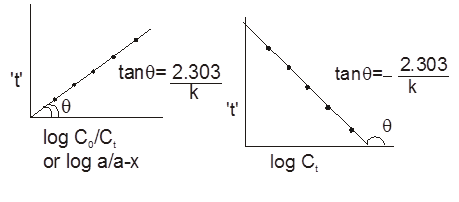
First order growth reaction :
For bacteria multiplication or virus growth use following concept Consider a growth reaction
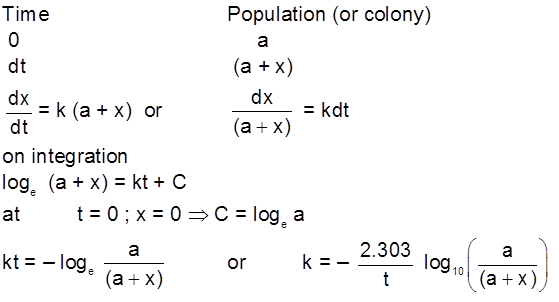
or
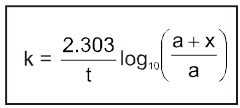
Generation time :
At ¾® t = generation time , x = a
t = ![]()
Examples of 1st order reactions :
1. H2O2 ¾® H2O + ![]() O2
O2
2. NH4 NO2 ¾® 2H2O + N2
3. Radiactive decay
All radioactive decays are always first order kinetics.
![]()
(c) Second order reaction :
2nd order Reactions
Two types
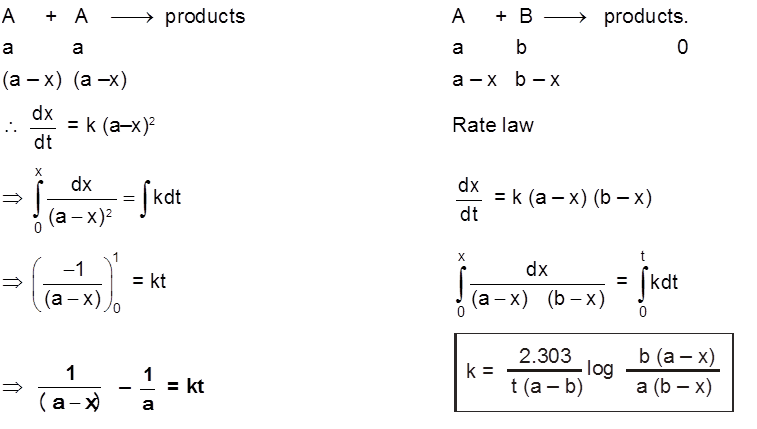
(d) Psuedo first order reaction :
A second order (or of higher order) reactions can be converted into a first order reaction if the other reactant is taken in large excess. Such first order reactions are known as psuedo first order reactions.
For A + B ¾® Products [Rate = K [A]1 [B]1]

Now if ‘B’ is taken in large excess b > > a.
![]()
‘b’ is very large can be taken as constant
Þ kb = log Þ k¢ = log
k¢ is psuedo first order rate constant
K’ will have units of first order.
K will have units of second order.
Examples of Pseudo 1st order reactions :
(a) Hydrolysis of canesugar
C12H12O11 + H2O ¾¾® C6H12O6 + C6H12O6
sucrose excess
(b) Hydrolysis of esters
CH3COOCH3 + H2O ![]() CH3COOH + CH3OH
CH3COOH + CH3OH
(excess)
Table : Characterstics of First-and Second-Order Reactions of the Type A Products

Graphical comparison of different orders
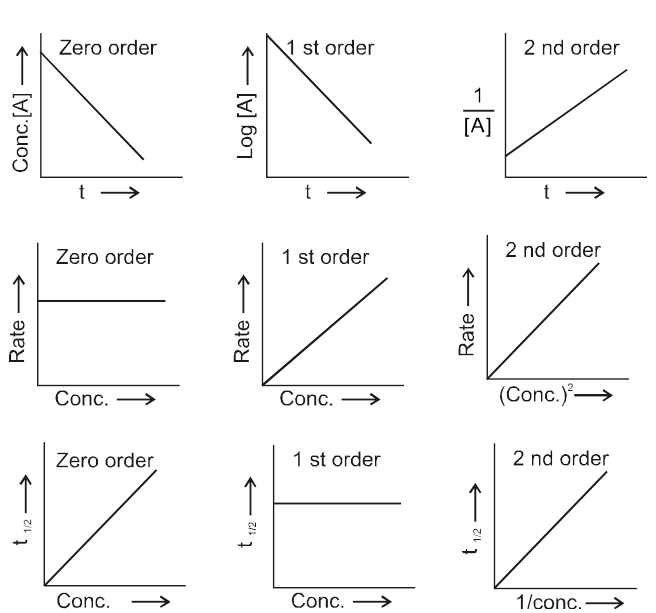
(A) integrated rate law method :
It is method of hit and trial. By checking where the kinetic data (experimetal data) best fits into which integrated rate law , we determine the order. It can also be done graphically.
(B) Method of half lives :
The half lives of each order is unique so by comparing half lives we can determine order
(C) Ostwald’s isolation method :
This method is useful for reaction which involve a large number of reactants. In this method, the concentration of all the reactants are taken in large excess exception that of one, so if
rate = k [A]a [B]b [C]c = k0 [A]a
Then value of ‘a’ can be calculated by previous methods and similarly ‘b’ and ‘c’ can also be calculated
4. Methods to monitor the progress of the reaction
- Books Name
- ACME SMART COACHING Chemistry Book
- Publication
- ACME SMART PUBLICATION
- Course
- CBSE Class 12
- Subject
- Chemistry
Methods to monitor the progress of the reaction :
(A) Pressure measurement :
Progress of gaseous reaction can be monitored by measuring total pressure at a fixed volume & temperature.
This method can applied for those reaction also in which a gas is produced because of decomposition of a solid or liquid. We can get an idea about the concentration of reacting species at a particular time by measuring pressure.
The pressure data can be given in terms of
(i) Partial pressure of the reactant
(ii) Total pressure of the reaction system
(iii) Pressure at only some points of time
(b) Volume measurement :
(i) By measuring the volume of product formed we can monitor the progress of reactions.
(c) Optical rotation measurment :
It is used for optically active sample. It is applicable if there is atleast one optically active species involved in chemical reaction.
The optically active species may be present in reactant or product.
It is found that 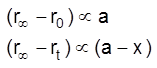
(a = concentration , x = amount consumed)
where arer0, rt, r¥ are angle of optical rotation at time t = 0, t = t and t = ¥
5. Effect of temperature on rate of reaction
- Books Name
- ACME SMART COACHING Chemistry Book
- Publication
- ACME SMART PUBLICATION
- Course
- CBSE Class 12
- Subject
- Chemistry
Effect of temperature on rate of reaction
In early days the effect of temperature on reaction rate was expressed in terms of temperature coefficient which was defined as the ratio of rate of reaction at two different temperature differing by 100C(usually these temperatures were taken as 250C and 350 C)
T.C. = ![]() 2 to 3 ( for most of the reactions)
2 to 3 ( for most of the reactions)
For some reactions temperature coefficient is also found to be less than unity. for example
2NO + O2 ® 2NO2 rate of reaction decreases on increasing temperature.
But the method of temperature coefficient was not exact and to explain the effect of temperature on reaction rate new theory was evolved
6. Arrhenius theory of reaction rate
- Books Name
- ACME SMART COACHING Chemistry Book
- Publication
- ACME SMART PUBLICATION
- Course
- CBSE Class 12
- Subject
- Chemistry
Arrhenius theory of reaction rate
It was developed by max Trautz and William lewis.
It gives insight in to the energetics and mechanistic aspects of reactions.
It is based upon kinetic theory of gases.
Arrhenius proposed a theory of reaction rate which states as follows :
A chemical reaction takes palce due to the collision among reactant molecules. The number of collisions taking place per second per unit volume of the reaction mixture is known as collision frequency (Z).
Every collision does not bring a chemical change. The collision that actually produce the products are effective collision. For a collision to be effective the following two barriers are to be effective the following two barriers are to be cleared.
Energy barrier :
The minimum amount of energy which the colliding molecules must posses as to make the chemical reaction to occur is known as threshold energy.
“The minimum amount of extra energy required by reactant molecules to pariticipate in a reaction is called activaiton energy (Ea)”
Orientation barrier :
Energy alone does not determine the effectiveness of the collision. The reacting molecules must collide in proper direction to make collision effective. Following diagrams can explain importance of suitable direction for collision.
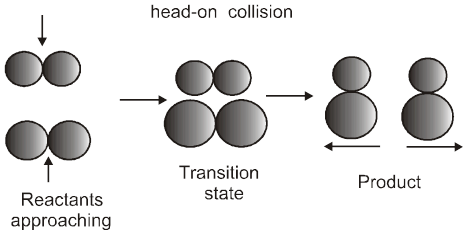
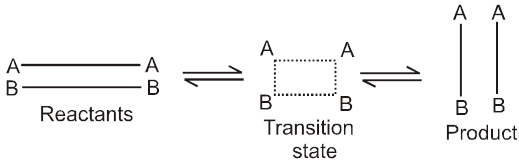
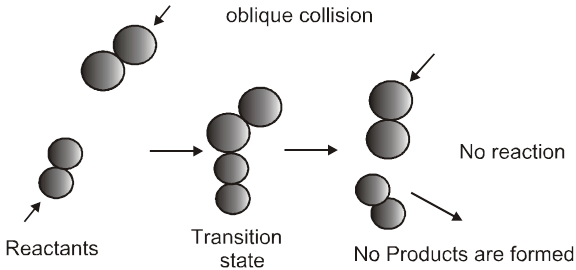
Collision to be effective the colliding molecules must posses some certain minimum energy called threshold energy of the reaction.
Reactant molecules having energy equal or greater than the threshold are called active molecules and those having energy less than the threshold are called passive molecules.
Concept of energy of activation (Ea)
he extra amount of energy which the reactant molecules (having energy less than the threshold) must acquire so that their mutual collision may lead to the breaking of bond(s) and hence the energy is known as energy of activation of the reaction. It is denoted by the symbol Ea. Thus,
Ea = Threshold energy – Actual average energy,
Ea is expressed in kcals mole–1 or kJ mole–1.
The essence of Arrhenius Theory of reaction rate is that there exists an energy barrier in the reaction path between reactant(s) and product(s) and for reaction to occur the reactant molecules must climb over the top of the barrier which they do by collision. The existence of energy barrier and concept of Ea can be understood from the following diagram.

Collision frequency is the number of collisions per unit
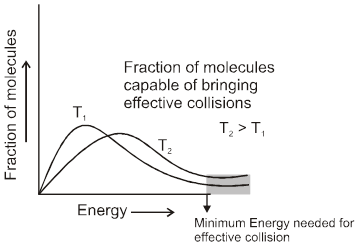
volume per unit time. It is denoted by the symbol Z. Z is directly proportional to ![]() . By 10ºC rise in temperature, so it is the fraction of the total number of effective collision that increases markedly resulting into marked increase in the reaction rate.
. By 10ºC rise in temperature, so it is the fraction of the total number of effective collision that increases markedly resulting into marked increase in the reaction rate.
Arrhenius equation 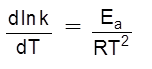
Integrating equation 4 assuming Ea to be constant we get,
lnk = –![]() or ln
or ln ![]() = –
= –![]() or k =
or k =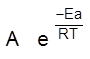
This is integrated form of Arrhenius equation.
Where, Constant A = pre–exponential factor it is a constant for a given reaction.
From this equation it is evident that as T ® ¥, k ® A. Thus, the constant A is the rate constant of reaction at infinity temperature. The rate constant goes on increasing with temperature.
So, when T approaches inifinty, k will be maximum. That is to say, A is the maximum rate constant of a reaction.
The expontential term i.e. e–Ea/RT measures the fraction of total number of molecules in the activated state or fraction of the total number of effective collisions.
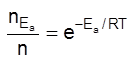
Where
nEa = no. of molecules of reactant in the activated state
n = total no. of molecules of the reactant in the reaction
From Arrhenius Equation we have,
log k =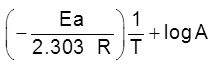
So from this it is evident that a plot of log k versus![]() will be a straight line of the slope equal to
will be a straight line of the slope equal to![]() and intercept equal to log A as shown below :
and intercept equal to log A as shown below :
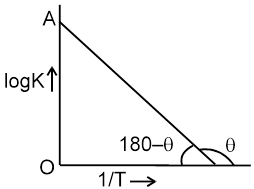
Thus, from this plot Ea and A both can be determined accurately.
If k1 and k2 be the rate constant of a reaction at two different temperature T1 and T2 respectively, then we have
log k1 = ![]() and
and
log k2 =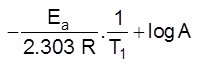
Subtracting we get 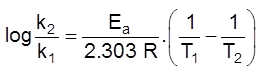
1. Adsorption
- Books Name
- ACME SMART COACHING Chemistry Book
- Publication
- ACME SMART PUBLICATION
- Course
- CBSE Class 12
- Subject
- Chemistry
Chapter 5
surface chemistry
Introduction :
Surface chemistry is that branch of chemistry which deals with study of the phenomena occuring at the surface or interface, i.e. at the boundary separating two bulk phases. In this chapter our main emphasis will be on three important topics related to surface chemistry, viz., adsorption, colloids and emulsions.
Adsorption
The phenomenon of attracting and retaining the molecules of a substance on the surface of a liquid or a solid resulting into a higher concentration of the molecules on the surface is called adsorption. As a result of adsorption, there is a decrease of surface energy. The process of removal of an adsorbed substance from the surface on which it is adsorbed is called desorption. It is the reverse of adsorption and can be brought about by heating or by reducing the pressure.
Adsorbent and adsorbate :The substance on the surface of which adsorption occurs is known as adsorbent. The substances that get adsorbed on the solid surface due to intermolecular attractions are called adsorbate.Charcoal, silica, gel, alumina gel are good adsorbents because they have highly porous structures and have large surface area. Colloids on account of their extremely small dimensions possess enoromous surface area per unit mass and are, therefore, also good adsorbents.
Examples of adsorption :
Adsorption of a gas by charcoal : Finely divided activated charcoal has a tendency to adsorb a number of gases like ammonia, sulphur dioxide, chlorine, phosgene, etc. In this case, charcoal acts as an adsorbent while gas molecules act as adsorbate.
Adsorption of a dye by charcoal : Animal charcoal is used for decolourising a number of organic substances in the form of their solutions. The discharge of the colour is due to the fact that the coloured component (generally an organic dye) gets adsorbed on the surface of the adsorbent (animal charcoal).
Sorption : When both adsorption and absorption take place simultaneously.
Eg : Dyes get adsorbed as well as absorbed in the cotton fibre i.e. sorption takes place.
Difference between adsorption and absorption :
The terms adsorption and absorption are different. Adsorption is a phenomenon in which there is higher concentration of another substance on the surface than in the bulk. On the other hand, absorption is a phenomenon in which the molecules of a substance are uniformly distributed throughout the body of other substance. For example, when silica gel is placed in the environment of water, it adsorbs the water vapour. The water vapour are present in high concentration at the surface of silica gel. On the other hand, when calcium chloride is placed in the environment of water, it absorbs water. The water vapour uniformly get distributed throughout the body of calcium chloride. Thus, silica gel adsorbs water vapour while anhydrous calcium chloride absorbs water.
Thermodynamics of adsorption : Adsorption is an exothermic process. Therefore DH of adsorption is always negative. When a gas is adsorbed the entropy of the gas decreases i.e. DS is negative. Adsorption is thus accompanied by decrease in enthalpy as well as entropy of the system, for a process to be spontaneous requirement is that DG must be negative. On the basis of equation, DG = DH - TDS, DG can be negative if DH has sufficiently high negative value as - TDS is positive. Thus, in an adsorption process, which is spontaneous, DS is negative, and DH is also sufficiently negative and as a combination of these two factors, DG is negative.
H becomes less and less negative as adsorption proceeds further and further. Ultimately DH becomes equal to TDS and DG becomes zero. This is the state at which equilibrium is attained.
Enthalpy of adsorption DHadsorption : It is the amount of the heat released when 1 mole of an adsorbate gets adsorbed on a particular adsorbent at adsorption equilibrium. It depends upon the nature of both the adsorbate as well as adsorbent.
Types of adsorption : The adsorption is classified into two types :
(i) Physical adsorption (i.e. physisorption) : When the particles of the adsorbate are held to the surface of the adsorbent by the physical forces such as van der Waal’s forces, the adsorption is called physical adsorption or vanderwaals adsorption.
(ii) Chemical adsorption (i.e. chemisorption) :
When the molecules of the adsorbate are held to the surface of the adsorbent by the chemical forces, the adsorption is called chemical adsorption.
Difference between physical adsorption and chemical adsorption

Competitive adsorption : When an adsorbent is in contact with more than one species (adsorbate). There will be competition among them to get adsorbed on to the surface of the adsorbent. The one that is more strongly adsorbed gets deposited first in preference to the others. Further a strongly adsorbed substance may displace a weakly adsorbed substance.
Ex. NH3 can displace O2 or N2 from the surface of charcoal.
Adsorption of gases on solids :
The extent of adsorption of a gas on a solid surface is affected by the following factors:
The nature of the gas (i.e. nature of the adsorbate). The easily liquefiable gases such as HCl, NH3, Cl2 etc. are adsorbed more than the permanent gases such as H2, N2 and O2. The ease with which a gas can be liquefied is primarily determined by its critical temperature. Higher the critical temperature (Tc) of a gas, the more easily it will be liquefied and, therefore, more readily it will be adsorbed on the solid.
Gas SO2 CH4 H2
TC 330K 190 K 33 K
Nature of adsorbent. The extent of adsorption of a gas depends upon the nature of adsorbent. Activated charcoal (i.e. activated carbon), metal oxides (silica gel and aluminium oxide) and clay can adsorb gases which are easily liquified. Gases such as H2, N2 and O2 are generally adsorbed on finely divided transition metals Ni and Co.
Activation of adsorbent :
(a) Metallic adsorbents are activated by mechanical rubbing or by subjecting it to some chemical reactions.
(b) To increase the adsorbing power of adsorbents, they are sub-divided into smaller pieces. As a results, the surface area is increased and therefore, the adsorbing power increases.
Effect of temperature :Mostly the process of adsorption is exothermic and the reverse process or desorption is endothermic. If the above equilibrium is subjected to increase in temperature, then according to Le-Chaterlier’s principle, with increase in temperature, the desorption will be favoured. Physical adsorption decreases continuously with increase in temperature whereas chemisorption increases initially, shows a maximum in the curve and then it decreases continuously.
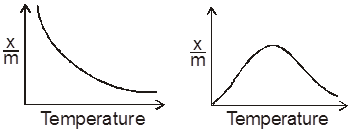
The initial increase in chemisorption with increase in temperature is because of activation energy required.
This is why the chemical adsorption is also known as “Activated adsorption”.
A graph between degree of adsorption (x/m) and temperature ‘t’ at a constant pressure of adsorbate gas is known as adsorption isobar.
Effect of pressure. The extent of adsorption of a gas per unit mass of adsorbent depends upon the pressure of the gas. The variation of extent of adsorption expressed as x/m (where x is the mass of adsorbate and m is the mass of the adsorbent) and the pressure is given as below. A graph between the amount of adsorption and gas pressure keeping the temperature constant is called an adsorption isotherm.
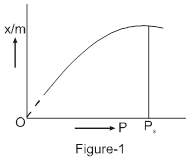
It is clear from the figure-1 that extent of adsorption (x/m) increases with pressure and becomes maximum corresponding to pressure Ps called equilibrium pressure. Since adsorption is a reversible process, the desorption also takes place simultaneously. At this pressure (Ps) the amount of gas adsorbed becomes equal to the amount of gas desorbed.
Freundlich Adsorption isotherm :
The variation of extent of adsorption (x/m) with pressure (P) was given mathematically by Freundlich.
At low pressure the graph is almost straight line which indicates that x/m is directly proportional to the pressure. This may be expressed as :
(x/m) a p or (x/m) = kp where k is constant.
At high pressure the graph becomes almost constant which means that x/m becomes independent of pressure. This may be expressed as :
(x/m) = constant or (x/m) a p0 (since p0 = 1) or (x/m) = kp0.
hus, in the intermediate range of pressure, x/m will depend upon the power of pressure which lies between 0 to 1, fractional power of pressure. This may be expressed as
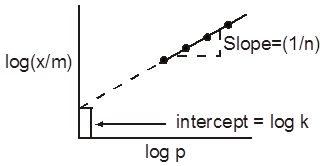
(x/m) a p1/n or (x/m) = kp1/n
Where n can take any whole number value which depends upon the nature of adsorbate and adsorbent. The above relationship is also called Freundlich’s adsorption isotherm.
The constant k and n can be determined as explained below : Taking logarithms on both sides of
Eq. (x/m) = kp1/n we get
log (x/m) = logk + (1/n) log p.
One of the drawbacks of Freundlich isotherm is that it fails at high pressure of the gas.
This equation applicable only when adsorbate substance form unimolecular layer on adsorbent surface. i.e. chemical adsorption.
Adsorption from solutions : The process of adsorption can take place from solutions also. It is observed that solid adsorbents adsorb certain solutes from solution in preference to other solutes and solvents. For example, animal charcoal decolouries impure sugar solution by adsorbing colouring dye in preference to sugar molecules.
The extent of adsorption from solution depends upon the concentration of solute in the solution as given by Freundlich isotherm :
(x/m) = k(c)1/n (n ![]() 1)
1)
where c is the equilibrium concentration of the solute in solution.
Temperature dependence here also is similar to that for adsorption of gases and in place of equilibrium pressure, we use equilibrium concentrations of the adsorbates in the solution.
Applications of adsorption :
In gas masks : Activated charcoal is generally used in gas masks to adsorb poisonous and toxic gases from air. These masks are commonly used by the miners because there are poisonous gases like CO, CH4 etc. in the atmosphere in coal mines.
In dyeing of cloths : Mordants such as alums are used in dyeing of cloths. They adsorb the dye particles which, otherwise, do not stick to the cloths.
In dehumidizers : Silica gel is commonly used to adsorb humidity or moisture from air.
Removal of colouring matter : Many substances such as sugar, juice and vegetable oils are coloured due to the presence of impurities. They can be decolourised by placing them in contact with adsorbents like activated charcoal or fuller’s earth.
Heterogeneous catalysis : The phenomenon of adsorption is useful in the heterogeneous catalysis. The metals such as Fe, Ni, Pt, Pd, etc, are used in the manufacturing processes such as Contact process, Haber process and the hydrogenation of oils. Their use is based upon the phenomenon of adsorption.
Refining Petroleum : Silica gel is used as adsorbent in petroleum refining.
Chromatography : It is a method for separation of component and is based on preferential adsorption column is very common device used.
Creating vacuum : High vacuum can be created by removing gas by adsorption.
Adsorption Indicators : In volumetric analysis, adsorption indicator is used Surface of certain precipitates such as silver halide have the property of adsorbing some dye like eosin, fluorescein, etc In the case of precipitation titration (AgNO3 vs NaCI) of the indicator is adsorbed at the end point producing a characteristic colour on the precipitate.
In froth floatation process : (in metallurgy).
Softening of hard water : Ion exchange resins used for softening of hard water is based upon selective and competive adsorption of ions on resins.
Na2Z + Ca+2 ![]() CaZ + 2Na+
CaZ + 2Na+
The organic polymers containing groups like –COOH, –SO3H and –NH2 etc. possess the property of selective adsorption of ions from solution. These are quite useful in the softening of water.
1. Occurrence of metals old
- Books Name
- ACME SMART COACHING Chemistry Book
- Publication
- ACME SMART PUBLICATION
- Course
- CBSE Class 12
- Subject
- Chemistry
Chapter 6
General principles and processes of isolation of elements
Introduction :
The compound of a metal found in nature is called a mineral. The minerals from which metal can be economically and conveniently extracted are called ores. An ore is usually contaminated with earthy or undesired materials known as gangue. So all minerals are not ores but all ores are minerals. Ores may be classified mainly into following four classes.
(a) Native ores : They contain the metal in free state. Silver, gold, platinum etc, occur as native ores.
(b) Oxidised ores : These ores consist of oxides or oxysalts (e.g. carbonates, phosphates, sulphates and silicates ) of metals.
(c) Sulphurised ores : These ores consist of sulphides of metals like iron, lead, zinc, mercury etc.
(d) Halide ores : These ores consist of halides of metals.
Important ore :
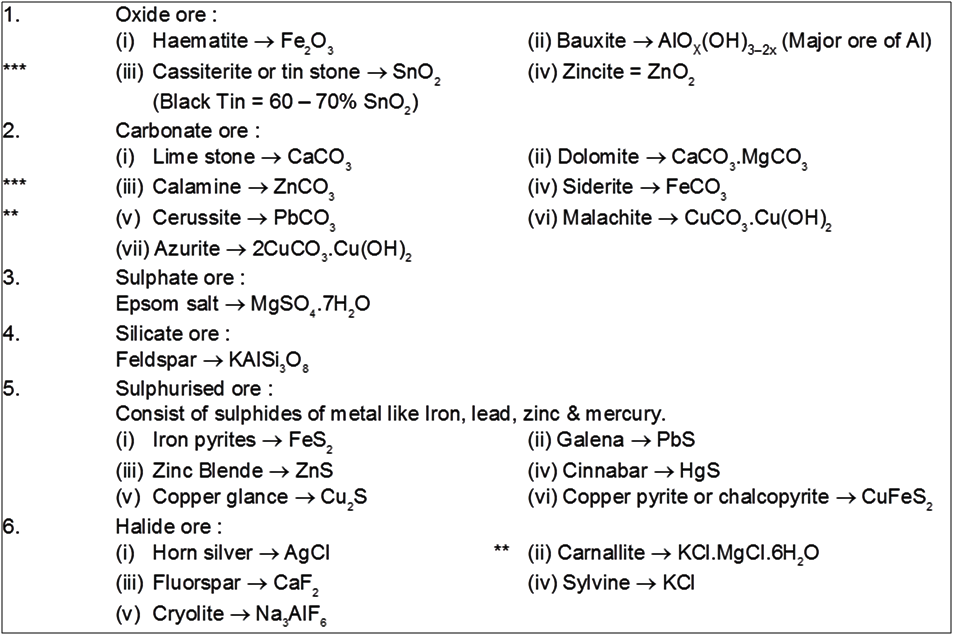
Note : Mg obtained from both sea water & earth crust.
Metallurgy :
The scientific and technological process used for the extraction/isolation of the metal from its ore is called as metallurgy.
The isolation and extraction of metals from their ores involve the following major steps:
(A) Crushing of the ore.
(B) Dressing or concentration of the ore.
(C) Isolation of the crude metal from its ore
(D) Purification or refining of the metal.
Chart1:
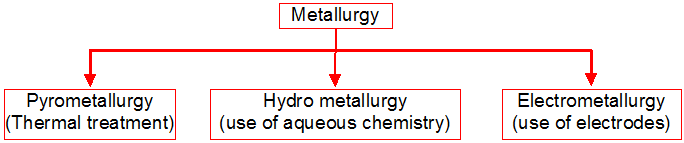
Chart2: Steps involved in metallurgy.
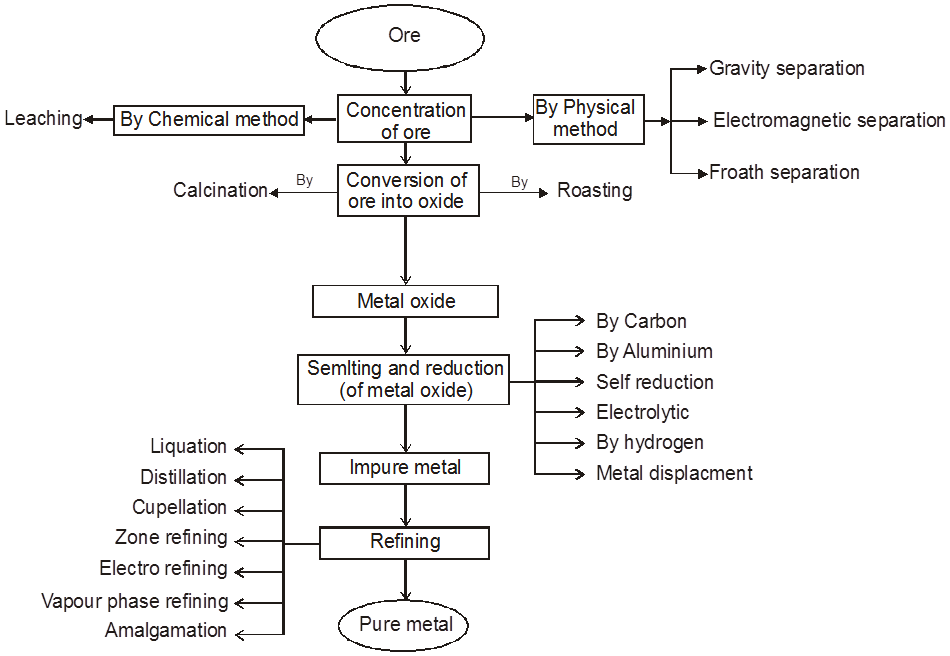
1. Physical Method :
(A) Crushing and Grinding : The ore is first crushed by jaw crushers and ground to a powder (pulverisation of the ore) in equipments like ball mills and stamp mills.
(B) Concentration : The removal of unwanted useless impurities from the ore is called dressing, concentration or benefaction of ore.
It involves several steps and selection of these steps depends upon the difference in physical properties of the compound of metal and that of gangue. Some of the important procedures are described below.
(i) Hydrolytic washing :
Gravity separation or "Levigation". Based on the difference in the densities of the gangue and ore particle.
Generally used for the concentration of oxide & native ore.
(ii) Electromagnetic sepration :
Based on difference in magnetic properties of mineral and gangue particle.
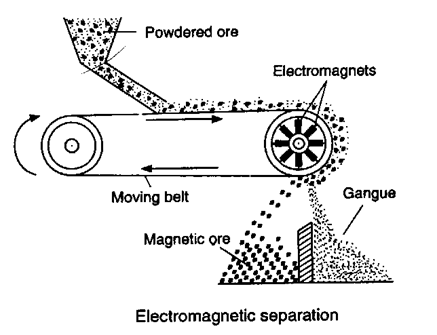
(a) Chromite ore [FeO.Cr2O3] is seprated from non magnetic silicious impurities.
(b) Cassiterite ore [SnO2] is seprated from magnetic wolframite [FeWO4 + MnWO4]
(iii) Froth floatation process :
Generally used for concentration of low grade sulphide ore PbS, ZnS, Cu2S, CuFeS2
Principle :
Based on fact that mineral & gangue particles have different wettability in water and oil (pine oil used)
Mineral particle ® are wetted by oil.
Gangue particle ® Wetted by water.
Reagents Used :
(i) Frothers :
These form stable froth which rises to the top of the flotation cell.
Oil like pine oil, comphor oil are used in small quantities.
Main Function of :
Frother ® Stick to ore & then take it to rise upto the top.
Stabilizer ® To stabilize the froth, froth stabilizer like [cresol & aniline] are added.
(ii) Collector :
K+ or Na+ ethyl xanthates![]() (R = alkyl,M+ = Na+ , K+) are used as collectors. Which collect or attract mineral partical and make them water repellant.
(R = alkyl,M+ = Na+ , K+) are used as collectors. Which collect or attract mineral partical and make them water repellant.
Main Function : Make the ore hydrophobic.
(iii) Activating & Depressing agents :
In PbS + ZnS + FeS2 mixture NaCN + Na2CO3 is used to depress the floation properties of ZnS & FeS2.
ZnS + CN– ¾® [Zn(CN)4]2–
FeS2 + CN– ¾® [Fe(CN)6]4–
CuSO4 is then added which is activating for ZnS as Cu forms more stable complexing with CN– than Zn2+
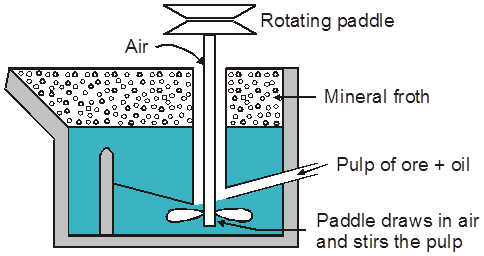
2. Chemical Method :
(4) Leaching :
Used when ore is soluble in some suitable solvent like ® acid, base & suitable chemical reagent.
Ex. (a) Leaching of alumina from bauxite.
(b) Extraction of Ag & Au from their ores in the complex form by treatment with NaCN & KCN.
(c) Treatment of low grade Cu ores with conc. H2SO4.
(C) Extraction of crude metal from concentrated ore :
The concentrated ore must be converted into a form which is suitable for reduction. Usually the sulphide ore is converted to oxide before reduction. Oxides are easier to reduce. Thus isolation of metals from concentrated ore involves two major steps as given below.
(i) Conversion to oxide
(ii) Reduction of the oxide to metal.
(i) Conversion to oxide :

Conversion of ore into oxide is carried out in two ways depending upon the nature of ore.
Calcination. It is a process of heating the concentrated ore strongly in a limited supply of air or in the absence of air. The process of calcination brings about the following changes :
(a) The carbonate ore gets decomposed to form the oxide of the metal, e.g.,
FeCO3 (siderite) ![]() FeO + CO2
FeO + CO2
PbCO3 (cerrussite) ![]() PbO + CO2
PbO + CO2
CaCO3 (calcite ore / lime stone) ![]() CaO + CO2
CaO + CO2
ZnCO3 (calamine) ![]() ZnO + CO2
ZnO + CO2
CuCO3.Cu(OH)2 (malachite) ![]() 2CuO + H2O + CO2
2CuO + H2O + CO2
MgCO3.CaCO3 (dolomite) ![]() MgO + CaO + 2CO2
MgO + CaO + 2CO2
(b) Water of crystallisation present in the hydrated oxide ore gets lost as moisture, e.g.,
2Fe2O3.3H2O (limonite) ![]() 2Fe2O3(s) + 3H2O(g)
2Fe2O3(s) + 3H2O(g) 
Al2O3. 2H2O (bauxite) ![]() Al2O3 (s) + 2H2O(g)
Al2O3 (s) + 2H2O(g) 
c) Organic matter, if present in the ore, gets expelled and the ore becomes porous. Volatile impurities are removed.
Roasting :
Generally used for sulphide ore.
Process : Concentrated ore is strongly heated in excess of air or O2 below its metling point.
(a) Roasting at moderate temperature :
2PbS + 3O2 ![]() 2PbO + 2SO2
2PbO + 2SO2
2ZnS + 2O2 ![]() 2ZnO + 2SO2
2ZnO + 2SO2
If temperature is low (500°C) & concentration of SO2 is high sulphate are produced.
PbS + 2O2 ![]() PbSO4
PbSO4
ZnS + 2O2 ![]() ZnSO4
ZnSO4
(b) Roasting at High temperature :
Self reduction / auto reduction / air reduction :
Sulphide ore of Cu, Pb, Hg & Sb when strongly heated in free supply of air, directly reduced to the metal this known as self reduction.
Cu2S (Copper glance) + O2 ¾® 2Cu + SO2
PbS (Gelena) + O2 ¾® Pb + SO2
HgS (Cinabar) + O2 ¾® Hg + SO2
Important Points
1.It remove impurities of As as As2O3, sulphur as SO2, P as P4O10 & Sb as Sb2O3
4M (M = As, Sb) + 3O2 ¾® 2M2O3↑
S + O2 ¾® SO2↑
P4 + 4O2 ¾® P4O10↑
2. Impurities of CuS & FeS in SnO2 converted to CuSO4 & FeSO4
CuS + 2O2 ![]() CuSO4
CuSO4
FeS + 2O2 ![]() FeSO4
FeSO4
Note : Calcination & Roasting carried out in a reverberatory furnace.
Smelting :
Slag formation : In many extraction processes, an oxide is added deliberately to combine with other impurities and form a stable molten phase immiscible with molten metal called a slag. The process is termed smelting.
The principle of slag formation is essentially the following :
Nonmetal oxide (acidic oxide) + Metal oxide (basic oxide) ¾® Fusible (easily melted) slag
Removal of unwanted basic and acidic oxides: For example, FeO is the impurity in extraction of Cu from copper pyrite.
2CuFeS2 + 4O2 ¾® Cu2S + 2FeO + 3SO2
Cu2S + FeO + SiO2 ¾® FeSiO3 (Fusible slag) + Cu2S (matte)
![]() (upper layer) (lower layer)
(upper layer) (lower layer)
Matte also contains a very small amount of iron(II) sulphide.
To remove unwanted acidic impurities like sand and P4O10, smelting is done in the presence of limestone.
CaCO3 ¾® CaO + CO2
CaO + SiO2 ¾® CaSiO3 (fusible slag)
6CaO + P4O10 ¾® 2Ca3(PO4)2 (fusible slag - Thomas slag)
Properties of a slag :
(i) Slag is a fusible mass.
(ii) It has low melting point.
(iii) It is lighter than and immiscible with the molten metal. It is due to these impurities that the slag floats as a separate layer on the molten metal and can thus be easily separated from the metal. The layer of the slag on the molten metal prevents the metal from being oxidised.
Type of flux : Fluxes are of two types viz., acidic flux and basic flux.
(a) Acidic flux : It is an acidic oxide (oxide of a non-metal) like SiO2, P2O5, B2O3 (from borax). It is used to remove the basic impurity like CaO, FeO, MgO etc. The acidic flux combines with the basic impurity and forms a slag.
(b) Basic flux : It is a basic oxide (i.e., oxide of a metal) like CaO (obtained from lime stone, CaCO3), MgO (from magnesite, MgCO3), haematite (Fe2O3) etc. It is used to remove the acidic impurity like SiO2, P2O5 etc. The basic flux combines with the acidic impurity and forms a slag.
Thus, slag can be defined as a fusible mass, which is obtained when a flux reacts with an infusible acidic or basic impurity present in the oxide ore.
Reduction of a Metal Oxide
(1) Reduction with Carbon :
PbO + C ¾® Pb + CO
2Fe2O3 + 3C ¾® 4Fe + 3CO2
*** ZnO + C ![]() Zn + CO (Extraction of Zn)
Zn + CO (Extraction of Zn)
*** SnO2 + 2C ![]() Sn + 2CO
Sn + 2CO
(2) Reduction with CO :
Fe2O3 + 3CO ¾® 2Fe + 3CO2
Fe3O4 + 4CO ¾® 3Fe + 4CO2
Reduction with C & CO is carried out in blast furnace.
(3) Redution with Al :
GoldSchmidt or Aluminothermic process :
Metallic oxide of Cr & Mn reduced by Al & this reaction is known as thermite reaction.
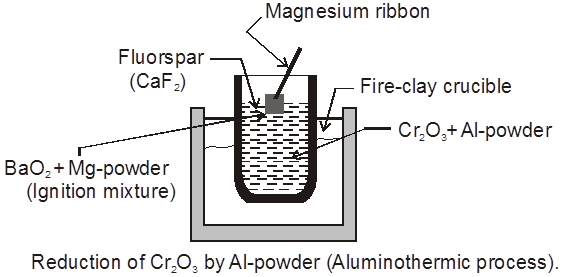
Mg + BaO2 ¾® BaO + MgO + Heat
(i) Cr2O3 + Al ¾® 2Cr(l) + Al2O3
*** (ii) 3Mn3O4 + 8Al ¾® 4Al2O3 + 9Mn
(iii) 2Al + Fe2O3 ¾®Al2O3 + 2Fe
(iv) B2O3 + 2Al ¾® 2B + Al2O3
(4) Redution by Mg & Na :
(i) TiCl4 + 2Mg ![]() Ti + 2MgCl2
Ti + 2MgCl2
(ii) TiCl4 + 4Na ![]() Ti + 4NaCl
Ti + 4NaCl
(5) Self reduction or auto reduction or air reduction :
Sulphide ore of some of the metal like Hg, Cu, Pb & Sb, when heated in air some part of these ore change into oxide or sulphate, thenthat part react with remaing part of sulphide ore to give its metal & sulphur dioxide.
This process is known as self reduction.
Ex. (i)(a) 2PbS + 3O2 ¾®2PbO + 2SO2
2PbO + PbS ¾®3Pb + SO2
(b) PbS + 2O2 ¾®PbSO4
PbSO4 + PbS ¾®2Pb + 2SO2
(ii) 2HgS + 3O2 ¾®2HgO + 2SO2
2HgO + HgS ¾®3Hg + SO2
(6) Electrolytic Reduction :
Electrolytic reduction is an expensive method than chemical method, that's why generally we do not use this method.
But when very high pure metal is required then we use this method.
This method is also used for highly reactive metal.
(i) Electrolyric reduction in aqueous solution :
This method is used when product does not react with water.
Electrolytic reduction of Cu & Zn from their sulphates.
(ii) In other solvents : Flourine react with water so it is produced by electrolysis of KHF2 dissolved in anhydrous HF.
(iii) In fused metal : When produced metal react with water, then metal is extracted from fused melt of their ionic salt.
Eg. (i) Al is extracted from electrolysis of fused mixture of Al2O3 and cryolite (Na3AlF6).
(ii) Extraction of Na by electrolysis of fused NaCl.
Note : In this electrolysis CaCl2 is added as impurity to lower the melting point from 800°C to 500°C.
(i) Hydro Metallurgy :
When metal can be extracted using solution without any heating or without any electrolysis then operation is known as hydrometallurgy.
Basic Step
(i) Dissolution of the valuable metal in aqueous solution.
(ii) Purification of leach solution.
(iii) Recovery of metal from purified solution.
Ex. Extraction of Ag & Au :
Metallic Ag dissolved in NaCN from ore of Ag & then precipitated with the help of Zn.
AgS(s) + 4CN¯ ¾® ![]() + S2–
+ S2–
2[Ag(CN)2]¯(aq) + Zn(s) ¾® [Zn(CN)4]2–(aq) + 2Ag(s)
(ii) Pyrometallurgy :
If furnace are used and ore are heated to extract metal then it is called pyrometallurgy.
Electrochemical principles of metallurgy :
Electrolytic reduction can be regarded as a technique for driving a reduction by coupling it through electrodes and external circuit to a reactive or a physical process with a more negative DG. The free energy available from the external source can be assessed from the potential it produces across the electrodes using the thermodynamic relation :
DG = –nFE ..........(i)
where n is the number of electrons transferred, F is Faraday’s constant (F = 96.5 kJ/mol) and Eº is electrode potential of the redox coupled formed in the system.
Hence, the total Gibb’s energy of the coupled internal and external process is
DG + DG (external) = DG – nFEext
If the potential difference of the external source exceeds
Eext = –![]()
the reduction is thermodynamically feasible; thus, the overall process occurs with a decrease in free energy.
More reactive metals have large negative values of the electrode potential. So their reduction is difficult. If the difference of two E0 values corresponds to a positive E0 and consequently negative D G0 in equation (i), then the less reactive metal will come out of the solution and the more reactive metal will go to the solution, e.g.,
Cu2+ (aq) + Fe(s) —® Cu(s) + Fe2+(aq)
In simple electrolysis, the Mn+ ions are discharged at negative electrodes (cathodes )and deposited there. Precautions are taken considering the reactivity of the metal produced and suitable materials are used as electrodes. Sometimes a flux is added for making the molten mass more conducting.
Hydrometallurgy : The processing of ores and minerals as well as metals and their compounds at relatively low, often ambient temperatures employing aqueous solution is known as hydrometallurgy. Occasionally, organic reagents are also used. This method of extraction is generally used for low grade ores. Copper is extracted by hydrometallurgy from low grade ore it is leached out using acid and bacteria. The solution containing Cu2+ is treated with scrap iron or H2.
CuSO4 + Fe —® Cu(s) + FeSO4
A hydrometallurgical process for the extraction of metals from ores, concentrates, or secondary materials essentially contains three basic steps—dissolution of the valuable metal in the aqueous solution (leaching) purification of leach solution and subsequent recovery of metal from the purified solutions either by electrolysis or by adding some electropositive metal to it.
Some of the metals obtained by hydrometallurgy are as follows :
(A) Extraction of Ag and Au : Metals like Au and Ag can be precipitated for their salt solution by electropositive metals for example, Zn.
Metallic Ag is dissolved from its ore in dilute NaCN solution, and the solute so obtained is treated with scrap Zn when Ag is precipitated. Air is blown into the solution oxidize Na2S. Leaching the metals like silver, gold with CN– is an oxidation reaction (Ag ® Ag+ or Au ® Au+)
Ag2S (s) + 4CN– (aq) —® 2 [Ag(CN)2]– (aq) + S2– (aq)
2[Ag(CN)2]– (aq) + Zn (s) —® [Zn (CN)4]2– (aq) + 2Ag (s)
4Au (s) + 8 CN– (aq) + O2 (g) + 2H2O (l)—® 4 [Au(CN)2]– (aq) + 4OH– (aq)
2[Au(CN)2]– (aq) + Zn (s) —® [Zn(CN)4]2– (aq) + 2 Au (s)
Here Zn acts as reducing agent.
(B) Extraction of Aluminium : It involves the following processes
(a) Purification of bauxite :
(1) Leaching of Alumina from bauxite :
If Fe2O3 is main impurity (red bauxite) ® Bayer's/Hall's
If SiO2 is main impurity (white bauxite) ® Serpeck's process.
(i) Bayer's process :

(iii) Serpeck's process :
Used for white bauxite containg silica as impurities.
Al2O3 + N2 + ![]() Coke AlN + CO ↑
Coke AlN + CO ↑
![]() Al(OH)3 + NH3 ↑
Al(OH)3 + NH3 ↑
![]() Al2O3 (pure)
Al2O3 (pure)
(2) Electrolytic reduction [Hall-Heroult process] :
Electrolysis of fused Al2O3 is difficult as its MP is very high (2323 K) & It is bed conductor of electricity in fused state.
So Al2O3 is mixed with Na3AlF6 or CaF2. Which lowers the MP (1173 K) & make alumina conducting.
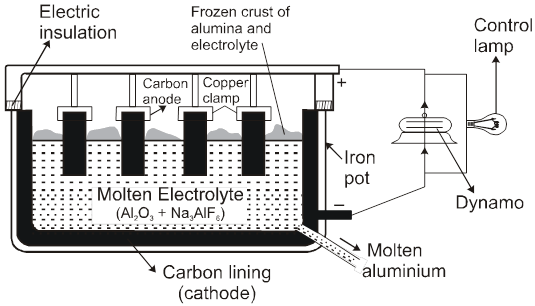
Cathode Þ Al3+ (Melt) + 3e– ® Al(l)
Anode Þ C(s) + O2– (Melt) ® CO(g) + 2e–
C(s) + 2O2– (Melt) ® CO2(g) + 4e–
Overall reaction Þ2Al2O3 + 3C ® 4Al + 3CO2
Note : During electrolytic reduction of aluminum, the carbon anodes are replaced from time to time because oxygen liberated at the carbon anodes react with anode to form CO & CO2.
Electrolytic refining of Al :
Hoop's process : For electrolytic refining of Al, Hoop's process is used.
Anode Þ Impure Al
Cathode Þ Pure Al
Electrolyte Þ Fused salt of Aluminium Fluoride
Note :The fused material remain in three different layer & remain separated because all the layer have different density.
Anode Þ Al(melt) ¾® Al3+ + 3e–
Cathode Þ Al3+ + 3e– ¾®Al
From anode (bottom layer), Al passes into solution as Al3+ ions and then from solution (middle layer) these Al3+ ion pass to cathode (top layer) and get reduced to pure metal.
Extraction of Na : The fused mixture of NaCl and CaCl2 is taken in Down’s cell which consists of circular iron cathode and carbon anode. On passing the electric current the following reactions take place :
Ionisation of NaCl : NaCl ![]() Na+ + Cl–
Na+ + Cl–
Collection of Na at cathode : Na+ + e– ® Na(Reduction).
Collection of Cl2 at anode : Cl– + e– ®Cl (Oxidation), Cl + Cl ® Cl2 .
Na can also be obtained by electrolysing molten NaOH in Castner’s cell.
Thermodynamics of extraction : Ellingham Diagram of a Metal
Ellingham Diagram
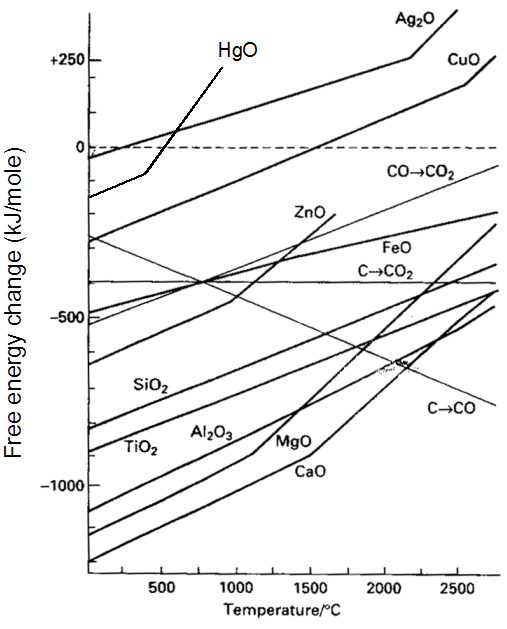
Thermodynamic of extraction :
For a Proces to be spontaneous D G must be negative.
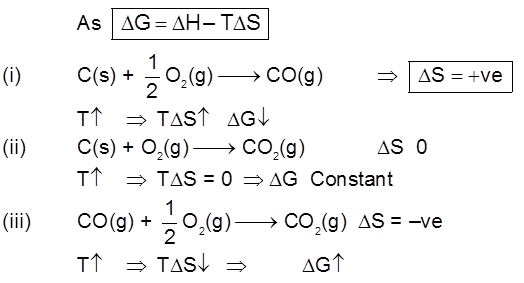
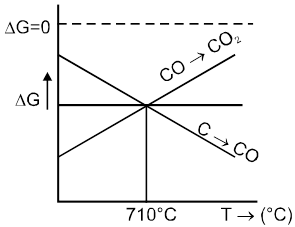
Ellingham Diagram of Metal
XM(s) + ![]() O2(g) ¾® MXOY(s)
O2(g) ¾® MXOY(s)
number of gaseous moles decreae with progress of reaction.
As DS = –ve If T Þ DG
Important Points
(1) Below 710°C, CO is better reducing agent than C.
(2) All the graphs are upgrowing and on increasing temperature, DG of formation of metal oxide become less negative, while on increasing temperature, DG of C ¾® CO reaction become more negative SO, C can reduce any metal from their metal oxide.
(3) Temperature above which DG of formation of metal oxide become positive, metal oxide become unstable & it decomposes into metal & oxygen.
(4) Theoritically, all metal oxide can be decomposed to give metal & oxygen, if suficiently high temperature is applied.
(5) When plot of one metal oxide is below the others then former metal is capable of reducing the later metal oxide into their metal.
Some important result
(1) All the three oxidation graph of carbon system are above the oxidation graph of ZnO upto temperature 1000°C. At this temperature C is thermodynamically capable of reducing ZnO to Zn. So C is better reducing agent for ZnO to Zn than CO.
(2) Below 1500°C temperature, the graph of MgO lies below the graph of Al2O3, so below this temperature Al cannot reduce MgO, but above this temperature graph of Al2O3 shifts below the graph of MgO so above 1500°C, Al can reduce MgO.
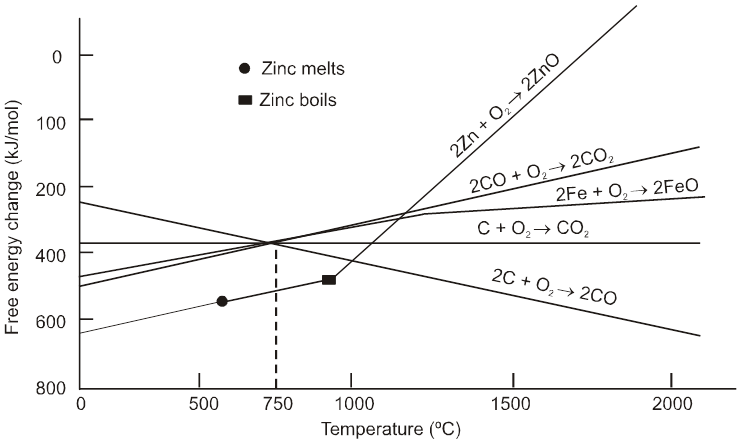
2. Catalysis
- Books Name
- ACME SMART COACHING Chemistry Book
- Publication
- ACME SMART PUBLICATION
- Course
- CBSE Class 12
- Subject
- Chemistry
Catalysts
Berzillus in 1835 used the word catalyst first time for some substance which alter rate of chemical reaction and themselves remain chemically and quantitatively unchanged after the reaction and the phenomenon is known as catalysis.
Eg : Potassium chlorate when heated at 653K to 873K, it gives O2, When MnO2 is used in this reaction the O2 is quickly at the low temperature hence MnO2 is a catalyst
2KCIO3 ® 2KCI + 3O2
Homogeneous Catalysis : When catalysts and reactants are in same phase then the process is said to be homogeneous catalysis and
Eg :
(i) ![]()
(ii) ![]()
(iii) 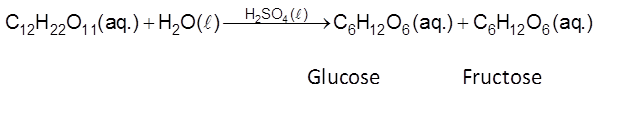
Heterogenous Catalysis : When catalysts and reactants are in different phases, then process a know as heterogenous catalysis and catalyst is called heterogeneous catalyst
Eg :
(i) ![]()
(ii) ![]()
(iii) ![]()
(iv) Vegetable oils![]() Vegetable ghee (s).
Vegetable ghee (s).
Types of Catalysis
(a) Positive Catalysis : A substance which increase the rate of chemical reaction is called positive catalyst and this process called positive catalysis.
(i) 
(ii) 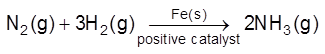
(b) Negative Catalysis : A substance which decrease the rate of chemical reaction is called negative catalyst and this process called negative catalysis.
Eg :
(i) 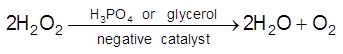
(ii) Decomposition of chloroform reduces in the presence of 1% ethyl alcohol.
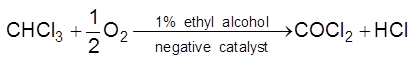
(iii) T.E.L. is used as negative catalyst in petrol which reduce knocking.
(c) Auto Catalysis : When one of the reaction product behave as catalyst for that reaction and increase the rate of reaction then the phenomenon is called autocatalysis.
“Auto catalytic reactions are slow in the beginning but become increasingly rapid as the reaction proceeds.
Eg :
(i) ![]()
(ii)
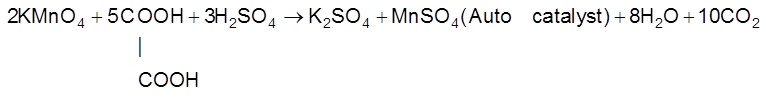
(d) Induced Catalyst : When one reaction catalyse an other reaction than the phenomenon is called induced catalysis and that reaction is called induced catalyst.
Promoters/Activators : Substance which themselves are not catalyst but its presence can increase the catalytic activity of catalyst. A promoters increase the number of active sites on the surface Eg :
(i) 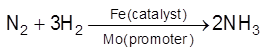
(ii) Vegetable Oil + H2 ![]() Vegetable ghee.
Vegetable ghee.
(iii) ![]()
Catalytic Poisons/ Anti catalysts/ Catalyst Inhibitor : Substance which themselves are not catalyst but whose presence decrease the activity of the catalyst. Poisoning is due to preferential adsorption of poison on the surface of the catalyst.
(i) 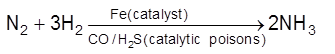
(ii) 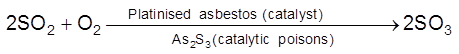
(iii)Rosunmund Reactions : ![]()
Characteristics of Catalysis :
(i) A Catalyst remains unchanged in mass and chemical compositions at the end of reactions. However its physical state can be change. Eg :
Granular MnO2 during decomposition of KClO3 is left as powder at the end of the reaction.
(ii) Finely devided state of catalyst is more efficient for the reactions because surface area increases and more adsorption take place.
(iii)A small amount of catalyst is generally sufficient to catalyse almost unlimited reaction but in some cases the rate of reaction depends on amount of catalyst.
Exception :
(a) In Friedal Craft reaction more amount of catalyst is required.
(b) Hydrolysis of ester in acidic and alkaline medium its rate of reaction is proportional to concentration of H+ or OH– ions.
(iv) A catalyst cannot initiate reaction. But some times the activation energy is so large that practically a reaction may not start until a catalyst lowers the activation energy significantly. For example, mixture of hydrogen and oxygen do not react at room temperature but the reaction occurs very rapid in presence of Pt black.
H₂ + O2 ![]() No reaction
No reaction
H₂ + O2 ![]() H2O.
H2O.
(v) Catalyst are generally specific in nature. A substance which act as a catalyst in a particular reaction, fails to catalyse other reaction.
(vi) Catalyst cannot change equilibrium state but it help to attain equilibrium quickly.
(vii) A catalyst does not change the enthalpy, entropy and free energy of a reaction.
(viii) Optimum temperature : There is a particular temperature at which the efficiency of a catalyst a maximum this temperature is known as optimum temperature. On either side the optimum temperature, the activity of catalyst decreases.
Adsorption Theory of Heterogeneous Catalyst : This theory explain the mechanism of heterogeneous catalyst. This theory is combination of two theory, intermediate compound formation theory and the old adsorption theory, the catalytic activity is localised on the surface on the catalyst. The mechanism involve 5 steps.
(i) Diffusion of reactant to the surface of the catalyst.
(ii) Adsorption of reactant molecules on the surface of the catalyst.
(iii) Formation of activated intermediate.
(iv) Formation of reactions product on the catalyst surface.
(v) Diffusion of reactions product from the catalyst surface or desorption.
Examples :
Let us consider addition of H2 gas to ethelene in presence of Ni catalyst, the reaction take places as follows.
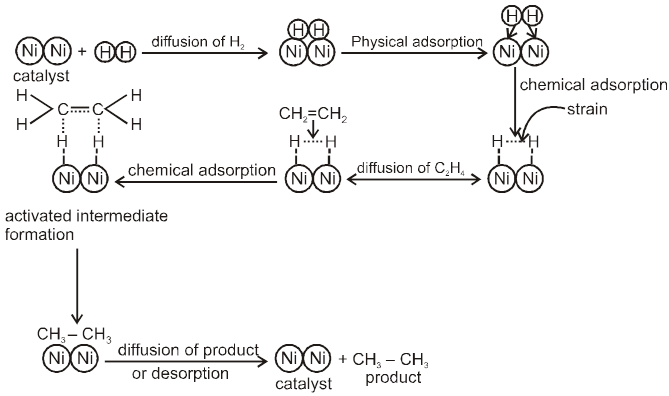
Factors Supporting Theory :
(i) This theory explain the role of active centre, more free valency which provide the more space for the more adsorption and concentration increases as a result increase in rate of reaction.
(ii) Rough surface has more active and pores there will be more free valency so more will be rate of reaction.
(iii) The theory explain centre action of promoters which occupied interstial void as a result surface area for the adsorption increases therefore rate of reaction increases.
(iv)The theory explain of function of poisons or inhibitors. In poisoning preferential adsorption of poisons take place on the catalyst, surface area for the adsorption on the catalyst decrease hence rate of reaction decreases.
Some Industrial Catalytic reactions

3. Colloids
- Books Name
- ACME SMART COACHING Chemistry Book
- Publication
- ACME SMART PUBLICATION
- Course
- CBSE Class 12
- Subject
- Chemistry
Colloid Solution
Colloid State : A substance is said to be in colloidal state when the size of the particle of disperse phase is greater than particle of true solution and less than that of suspension solution particle, their range of diameters between 1 and 1000 nm (10–9 to 10–6 m).
Colloid solution : It is a heterogeneous system consisting of 2 phase :
(1) Disperse Phase (D.P) : The phase which is dispersed through the medium is called dispersed phase or discontinuous phase or internal phase.
(2) Dispersion Medium (D.M) : A medium in which colloidal particles are dispersed is called dispersion medium. It is also known as continuous phase or outer phase or external phase.
Colloidal solution = D.P. + D.M.
Ex. In Gold sol, Gold is D.P and water is D.M.
Diffrenciating point of colloids :
(1) A colloid is a heterogeneous system in which one substance is dispersed (dispersed phase) as very fine particles in another substance called dispersion medium.
(2) The solution and colloid essentially differ from one another by particle size.
* In a solution, the particles are ions or small molecules.
* In a colloid, the dispersed phase may consist of particles of a single macromolecule (such as protein or synthetic polymer) or an aggregate of many atoms, ions or molecules.
(3) Colloidal particles are larger than simple molecules but small enough to remain suspended. They have a range of diameters between 1 and 1000 nm (10–9 to 10–6 m).
4. Classification of colloids
- Books Name
- ACME SMART COACHING Chemistry Book
- Publication
- ACME SMART PUBLICATION
- Course
- CBSE Class 12
- Subject
- Chemistry
Classification of colloids
1. On the basis of physical state of D.P. and D.M.
On the bases of physical state of D.P. and D.M. colloidal solution may be divided into eight system.
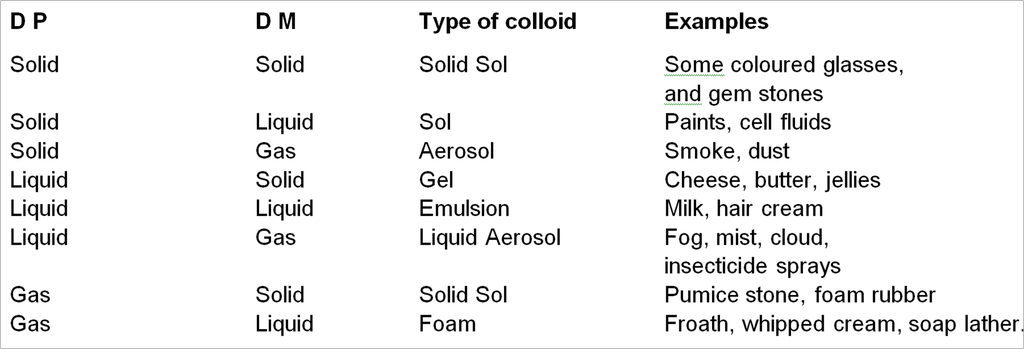
* Solution of gas in gas is not a colloidal system because it form homogeneous mixture.
2. On the Basis of interaction of D.P. for D.M. : There are two types-
(i) Lyophilic colloids / liquid loving sols / intrinsic colloid. The colloidal solution in which the particles of the dispersed phase have a great affinity (or love) for the dispersion medium, are called lyophilic colloids. These solutions are easily formed and the lyophilic colloids are reversible in nature. In case water acts as the dispersion medium, the lyophilic colloid is called hydrophilic colloid. The common examples of lyophilic colloids are glue, gelatin, starch, proteins, egg albumin, rubber, etc.
(ii) Lyophobic colloids / solvent hating colloid / extrinsic colloid. The colloidal solutions in which there is no affinity between particles of the dispersed phase and the dispersion medium are called lyophobic colloids. Such solutions are formed with difficulty only by special methods. These sols are readily precipitated (or coagulated) on the addition of small amounts of electrolytes, by heating or by shaking and hence are not stable. Further, once precipitated, they do not give back the colloidal sol by simple addition of the dispersion medium. Hence these sols are also called irreversible sols. They need stabilising agents for their preservation. In case the dispersion medium is water, the lyophobic sol is called hydrophobic colloid. For example, the solution of metals like Ag and Au, hydroxides like Al (OH)3, Fe(OH)3, metal sulphides like As2S3 etc.
* Lyophilic sols are more stable than lyophobic sols, the additional stability is due presence of an envelope of the solvent layer (say water) around the colloidal particle, the process is known as hydration, To coagulate a hydrophilic sols we have to add a dehydrating agent in addition to electrolyte.
distinction between lyophilic and lyophobic colloids
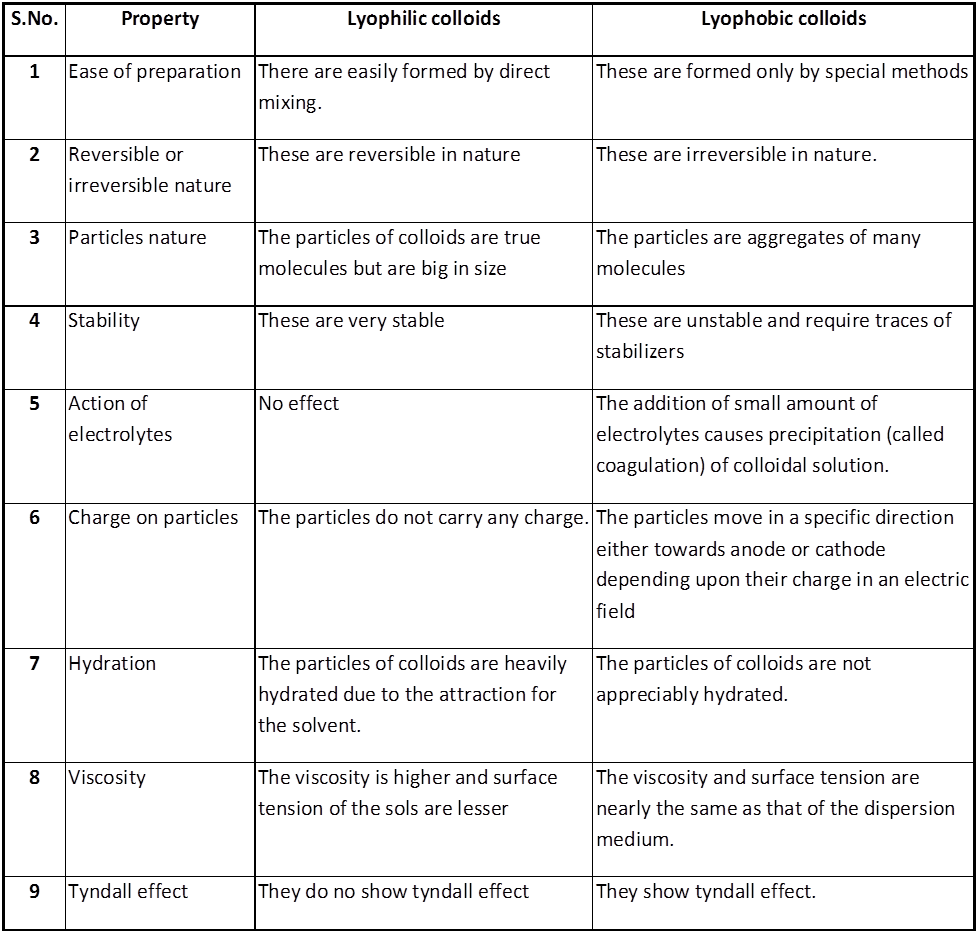
3. On the basis of charge of on particles
(i) positive Sol
(a) Metal Oxide & Hydroxide - SnO2, TiO2, Fe2O3, AI(OH)3, Fe(OH)3, Cr(OH)3.
(b) Basic Dyes Methylene blue, vismark brown.
(ii) negative Sol -
(a) Metal sol - Ag, Au, Pt, Cu
(b) Acidic dye - congo red, eosin
(c) Sulphide Sol- CdS, HgS, As2S3, Sb2S3.
(d) Natural sol - Blood, clay, charcoal, latex rubber, dust particle in water, starch carbon particle in smoke, gum.
4. Other type of colloids : Multimolecular, macromolecular and associated colloids
Multimolecular colloids : In this type, the particles consist of an aggregate of atoms or small molecules size less than 1 nm. For example, sols of gold atoms and sulphur (S8) molecules. In these colloids, the particles are held together by van der Waal’s forces.
Macromolecular colloids : In this types, the particles of the dispersed phase are sufficiently big in size (macro) to be of colloidal dimensions. These macromolecules forming the dispersed phase are generally polymers having very high molecular masses. These colloids are quite stable and resemble true solutions in many respects. Naturally occuring macromolecules are starch, cellulose, proteins, enzymes, gelatin, etc.
Associated colloids (Micelles): These are the substances which behave as normal strong electrolytes at low concentration but behave as colloidal particles at higher concentration. These associated particles are also called micelles. Ex. Soap.
Micelles : There are some substances which at low concentrations behave as normal strong electrolytes but at higher concentrations exhibit colloidal behaviour due to the formation of aggregated particles. The aggregated particles thus formed are called micelles. These are also known as associated colloids. The formation of micelles takes place only above a particular temperature called Kraft Temperature (Tk) and above a particular concentration called Critical Micelle Concentration (CMC). On dilution, these colloids revert back to individual ions. Surface active agents such as soaps and synthetic detergents belong to this class. For soaps, the CMC is ~ 10–4 to 10–3 mol L–1. These colloids have both lyophobic and lyophilic parts. Micelles may contain as many as 100 molecules or more.
Mechanism of micelle formation: Let us take the example of soap solutions. Soap is sodium salt of a higher fatty acid and may be represented as RCOO–Na+ e.g., sodium stearate viz.CH3(CH2)16COO– Na+ which is a major component of many bar soaps. When dissolved in water, it dissociates into RCOO- and Na+ ions. The RCOO– ions, however, consist of two parts i.e., long hydrocarbon chain R (also called non-polar 'tail') which is hydrophobic (water repelling) and the polar group COO– (also called polar-ionic 'head') which is hydrophilic (water loving). The RCOO– lons are, therefore, present on the surface with their COO– groups in water and the hydrocarbon chains R staying away from it, and remain at the surface, but at higher concentration these are pulled into the bulk of the solution and aggregate in a spherical form with their hydrocarbon chains pointing towards the centre with COO– part remaining outward on the surface. An aggregate thus formed is known as ‘Ionic micelle'. These micelles may contain as many as upto 100 such ions.
Aggregation of RCOO– ions to form an ionic micelle.
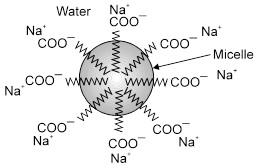
Similarly, in case of detergents, e.g., sodium lauryl sulphate viz. CH3(CH2)11SO4– Na+, the polar group is – SO4– along with the long hydrocarbon chain. Hence, the mechanism of micelle formation is same as that of soaps.
Critical micelle concentration [CMC] : The minimum concentration required for micelle formation is called critical micelle concentration. Its value depends upon the nature of D.P. and D.M. For eg. Surface active agent (surfactants, which decrease the surface tension) like soaps and detergents form micelle beyond CMC (~10–3 mol/litre for soaps).
* Usually longer the hydrophobic chain, smaller is its CMC.
* Also CMC increase with decreasing polarity of the D.M.
* The micelles ‘formation takes place only above a particular temperature called as Kraft Temperature (Tk ).
*At CMC, the micelles are spherical in shape, but that start flattening with increase in concentration and ultimately form sheet or film like structures which have a thickness of two molecules. These are called lamelar micelles or McBain Micelles.
Example of micelles :
(i) Sodium stearate C17H35COO–Na+(Soap).
(ii) Sodium lauryl sulphate CH3 [CH2]11 SO4– Na+ (Detergent).
(iii) Cetyl trimethyl ammonium bromide (Detergent). CH3(CH2)15N (CH3)3Br–.
(iv) Sodium p-dodecylbenzenesulphonate (Detergent) : ![]()
(v) Acidic (negative colloids) and basic (positive colloids) dyes.The Cleansing Action of Soaps : It has been mentioned earlier that a micelle consists of a hydrophobic hydrocarbon like central core. The cleansing action of soap is due to these micelles, because oil and grease can be solubilised in their hydrocarbon, like centres which are not otherwise soluble in water. This is shown diagrammatically in Figure The dirt goes out along with the soap micelles.

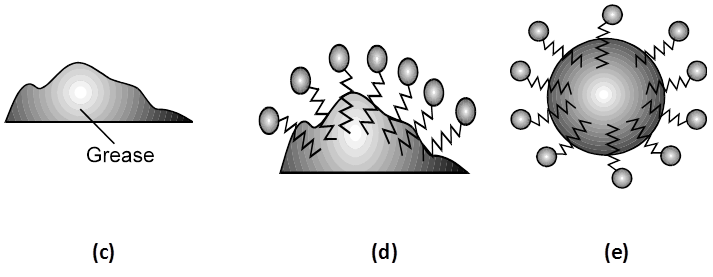
(a) A sodium stearate molecule
(b) The simplified representation of the molecule that shows a hydrophilic head and a hydrophobic tail
(c) Grease (oily substance) is not soluble in water
(d) When soap is added to water, the non-polar tails of soap molecules dissolve in grease
(e) Finally, the grease is removed in the form of micelles containing grease.
*Surfactants : They can be ionic as well as non-ionic. The ionic are soaps and detergent. The surfactant gets adsorbed at the interface between the dispersed droplets and dispersion medium in a form of mono molecular layer and lowers the interfacial tension between oil and water so as to facilitate the mixing of two liquids.
Preparation of lyophobic colloidal sols :
[A] Condensation methods :
In these methods particles of atomic or molecular size are induced to combine to form aggregates having colloidal dimensions. For this purpose chemical as well as physical methods can be applied.
(a) Chemical methods. Colloidal solutions can be prepared by chemical reactions leading to formation of molecules by double decomposition, oxidation, reduction or hydrolysis. These molecules then aggregate leading to formation of sols.
(i) Double decomposition : When a hot aqueous dilute solution of arsenous oxide (As2O3) is mixed with a saturated solution of H2S in water, a colloidal sol of arsenous sulphide (As2S3) is obtained.
As2O3(in hot water) + 3H2S (saturated solution in H2O) ![]() As2S3(sol) + 3H2O
As2S3(sol) + 3H2O
(ii) Oxidation : A colloidal sol of sulphur is obtained by passing H2S into a solution of sulphur dioxide.
SO2 + 2H2S(saturated solution in H2O) ![]() 3S(sol) + 2H2O
3S(sol) + 2H2O
Sulphur sol can also be obtained when H2S is bubbled through Br2 water or nitric acid (oxidizing agent).
(iii) Reduction : Colloidal sol of metals like gold, silver solution are obtained by following method.
2 AuCl3 + 3 HCHO + 3H2O 2Au(sol) + 3HCOOH + 6HCl.
(purple of cassius)
(iv) Hydrolysis : A colloidal sol of metal hydroxides like Al(OH)3 or Cr(OH)3 is obtained by boiling a dilute solution of FeCl3 , AlCl3 or CrCl3 .
FeCl3 + 3H2O Fe(OH)3 (sol) + 3HCl
AlCl3 + 3H2O Al(OH)3 (sol) + 3HCl
The colloidal sol of sillicic acid is also obtained by hydrolysis of dilute solution of sodium silicate with hydrochloric acid.
Na4SiO4 + 4HCl ![]() Si(OH)4 (sol) + 4NaCl.
Si(OH)4 (sol) + 4NaCl.
(b) Physical methods : The following physical methods are used to prepare the colloidal solutions.
(i) By Exchange of solvent : When a true solution is mixed with an excess of the other solvent in which the solute is insoluble but solvent is miscible, a colloidal sol is obtained. For example,
when a solution of sulphur in alcohol is poured in excess of water, a colloidal sol of sulphur is obtained.
when a solution of phenolphthalein in alcohol is poured in excess of water a white sol of phenolphthalein is found.
Phenolphthalein, I2 , sulphur sol can be prepared by this methods.
(ii) Excessive cooling : Molecules of certain substance condense together on excess cooling to form colloidal size particle. The colloidal sol of ice in an organic solvent such as CHCl3 or ether can be obtained by freezing a solution of water in the solvent. The molecules of water which can no longer be held in solution separately combine to form particles of colloidal size.
[B] Dispersion Methods : In these methods large particles of the substance are broken into particles of colloidal dimensions in the presence of dispersion medium. These are stabilized by adding some suitable stabilizer. Some of the methods employed are given below :
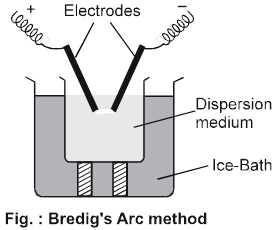
(a) Electrical disintegration or Bredig's Arc method : This process involves dispersion as well as condensation. Colloidal sols of less reactive metals such as gold, silver, platinum, copper, lead etc., can be prepared by this method. In this method, electric arc is struck between electrodes of the metal immersed in the dispersion medium as shown in fig. The intense heat produced vaporises the metal, which then condenses to form particles of colloidal size by surrounding cooling mixture (ice).
*A slight trace of KOH is added in water to stabilized colloidal solutions.
(b) Peptization: The term has originated from the digestion of proteins by the enzyme pepsin. Peptization may be defined as (the process of converting a precipitate into colloidal sol by shaking it with dispersion medium in the presence of a small amount of electrolyte)

The electrolyte used for this purpose is called peptizing agent. This method is applied, generally, to convert a freshly prepared precipitate into a colloidal sol. During peptization, the precipitate adsorbs one of the ions of the electrolyte on its surface. The ion adsorbed on the surface is common either with the anion or cation of the electrolyte. This causes the development of positive or negative charge on precipitates which ultimately break
up into smaller particles having the dimensions of colloids.
For example :
(i) When freshly precipitated Fe(OH)3 is shaken with aqueous solution of FeCl3 (peptizing agent) it adsorbs Fe3+ ions and thereby breaks up into small-sized particles.
FeCl3 ![]() Fe3+ + 3Cl– ;
Fe3+ + 3Cl– ;
Fe(OH)3 + Fe3+ ![]() Fe(OH)3 | Fe3+
Fe(OH)3 | Fe3+
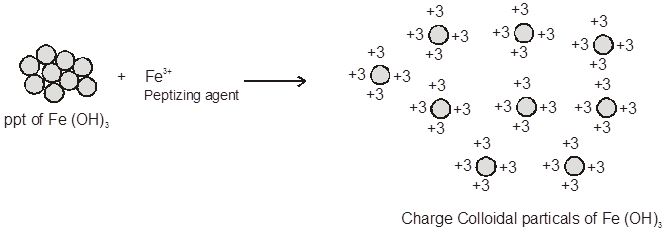
(ii) Freshly prepared stannic oxide on treatment with a small amount of dilute hydrochloric acid forms a stable colloidal sol of stannic oxide, SnO2 ; Sn4+ .
SnO2 + 4HCl ® Sn4+ + 2H2O + 4Cl–
SnO2 + Sn4+ ® SnO2 / Sn4+ .
(iii) Freshly precipitated silver chloride can be converted into a colloidal sol by adding a small amount of hydrochloric acid, AgCl : Cl– .
(iv) Cadmium sulphide can be peptised with the help of hydrogen sulphide, CdS : S2– .
Purification of Colloidal Sols : The colloidal sols obtained by various methods are impure and contain impurities of electrolytes and other soluble substances. These impurities may destabilise the sol. Hence, they have to be removed. A very important method of removal of soluble impurities from sols by a semipermeable membrane is known as dialysis.
A. Dialysis : It is a process of removing a dissolved substance from a colloidal solution by means diffusion through suitable membrane. Since particles in true solution (ions or smaller molecules) can pass through animal membrane or parchment paper or cellophane sheet but colloidal particle do not, the appratus used for this purpose is called Dialyser.
A bag of suitable membrane containing the colloidal solutions is suspended in a vessel through which fresh water continously flow. The molecules and ions (crystalloids) diffuse through membrane into the outer water & pure colloidal solution is left behind.
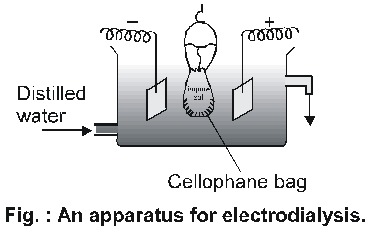
Movement of ions across the membrane can be expedited by applying electric potential through two electrodes as shown in fig.
This method is faster than simple dialysis and is known as
Electrodialysis.
*The most important applications of dialysis is in the purification of blood in the artificial kidney machine. In case of kidney failure, blood cannot be purified. under such condition, the blood is separated from dissolved toxic impurities by dialysis and re-introduced in the bloods stream.
*Dialysis is not applicable for non-electrolytes like glucose, sugar, etc.
B. Ultra Filtration : In this method, colloidal sols are purified by carrying out filtration through special type of graded filters called ultra-filters. These filter papers allow only the electrolytes to pass through. These filter papers are made of particular pore size by impregnating with colloidal solution and subsequently hardened by soaking in formaldehyde collodion. In order to accelerate the filtration through such filter papers, increased pressure or section is employed.
Important properties of colloidal sols :
Heterogeneous character :
Colloidal sols are heterogeneous in character as they consist of two phases.
(a) dispersed phase and (b) dispersion medium.
Visibility : Due to scattering caused by the colloidal particles, it will appear as a bright spot moving randomly.
Filterability :Colloidal particles pass through an ordinary filter paper. However, the particle do not pass through other fine membranes.
Colligative Properties : Colloidal sols show the colligative properties viz. relative lowering of vapour pressure, elevation in boiling point, depression in freezing point and osmotic pressure. However, due to high average molecular masses of colloidal particles, mole fraction of the dispersed phase is very low. Hence, the values of the colligative properties observed experimentally are very small. Only osmotic pressure measurements are used in determining the molecular mass of polymers.
Optical Properties-Tyndall effect : Tyndall, in 1869, observed that if a strong beam of light is passed through a colloidal sol placed in a dark place, the path of the beam gets illuminated. This phenomenon is called Tyndall effect, which is due to the scattering of light by the colloidal particles. The illuminated path of beam is called Tyndall cone. This phenomenon is due to scattering of light from the surface of colloidal particles. In a true solution there are no particles of sufficiently large diameter to scatter light & hence the beam is invisible.
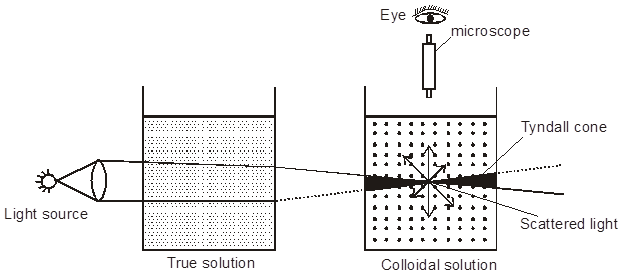
*The intensity of scattered light depends on the difference between the refractive indice of the D.P and D.M., In lyophobic colloids, this difference is appreciable and therefore the tyndal effect is quite well defined but in lyophilic sols the difference is very small and the tyndal effect is very weak. Thus in sols of silicic acid, blood serum, albumin, etc. there is little or no tyndal effect.
Example of Tyndall Effect
® Blue colour of sky and sea water.
® Visibility of tail of comets.
® Light thrown from a projector in cinema hall.
® Appearance of dust particle in a semi darked room.
Application of Tyndall Effect :
(i) In making ultramicroscopes.
(ii) In finding heterogenity of solution.
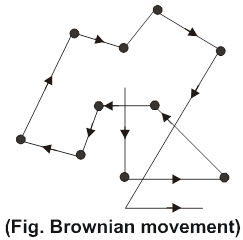
Brownian movement: Robert Brown, a botanist, discovered in 1827 that pollen grains placed in water do not remain at rest but move about continuously and randomly. Later on, this phenomenon was observed in case of colloidal particles when they were seen under an ultramicroscope. The particles were seen to be in constant zig-zag motion as shown in fig. This zig-zag motion is called Brownian movement.
Brownian movement arises because of the impact of the molecules of the dispersion medium with the colloidal particles. It has been postulated that the impact of the molecules of the dispersion medium on the colloidal particle are unequal leading to zig-zag motion. However, as the size of the particle increases, the effect of the impacts average out and the Brownian movement becomes slow. Ultimately, when the dispersed particle becomes big enough to acquire the dimensions of suspension, no Brownian movement is observed.
Factors Affecting Brownian Movement :
(i) If particles is large then brownian movement becomes less.
(ii) Brownian movement increases with increasing temperature.
(iii) The brownian movement does not change with time & remains same for months or even for a year.
Important :
(i) In confirmation of kinetic energy.
(ii) Determination of Avogadro numbers.
(iii) Stability of colloidal solution : Brownian movement does not allow the colloidal particles to settle down to gravity & thus is responsible for their stability.
Electrical Properties (Electrophoresis) : The particles of the colloids are electrically charged and carry positive or negative charge. The dispersion medium has an equal and opposite charge making the system neutral as a whole. Due to similar nature of the charge carried by the particles, they repel each other and do not combine to form bigger particles. That is why, a sol is stable and particles do not settle down. Arsenious sulphide, gold, silver and platinum particles in their respective colloidal sols are negatively charged while particles of ferric hydroxide, aluminium hydroxide are positively charged. The existence of the electric charge is shown by the phenomenon of electrophoresis. It involves the 'movement of colloidal particles either towards the cathode or anode, under the influence of the electric field'. The apparatus used for electrophoresis as shown in fig.

The colloidal solution is placed in a U-tube fitted with platinum electrodes. On passing an electric current, the charged colloidal particles move towards the oppositely charged electrode. Thus, if arsenic sulphide sol is taken in the U-tube, in which negatively charge particle of arsenic sulphide move towards the anode.
*Earlier this process was called cataphoresis because most of the colloidal sols studied at that time were positively charged and moved towards cathode.
Isoelectric point : The H+ concentration at which the colloidal particles have no charge is known as the isoelectric point. At this point stability of colloidal particles becomes very less & do not move under influence of electric field.
Fe(OH)3 sol prepared by the hydrolysis of FeCl3 solution adsorbs Fe3+ and this is positively charged.
FeCl3 + 3H2O ![]() Fe(OH3) + 3HCl
Fe(OH3) + 3HCl
Fe(OH)3 + FeCl3 ® Fe(OH)3 ![]() Fe3+ : 3Cl–
Fe3+ : 3Cl–
Fixed part Diffused part.
Positive charge on colloidal sol is due to adsorption of Fe3+ ion (common ion between Fe(OH)3 and FeCl3).
As2S3 colloidal sol is obtained when As2O3 is saturated with H2S :
As2O3 + 3H2S ®As2S3 + 3H2O.
As2S3 adsorbs S2– ions (common between H2S and As2S3 and thus is negatively charged).
As2S3 + H2S ® As2S3 ![]() S2– : 2H+.
S2– : 2H+.
AgI in contact with AgNO3 forms positively charged colloidal sol due to adsorption of Ag+ ion.
AgI + AgNO3 ® [AgI]Ag+ : NO3– , AgI in contact with KI forms negatively charged colloidal sol due to adsorption of I– ion AgI + KI ® AgI  I– : K+.
I– : K+.
SnO2 in acidic medium forms positively charged colloidal sol due to adsorption of Sn4+ formed.
SnO2 + 4H+ ® Sn4+ + 2H2O
SnO2 + Sn4+ ® SnO2 ![]() Sn4+
Sn4+
SnO2 in alkaline medium forms negatively charged colloidal sol due to adsorption of SnO32– formed.
SnO2 + 2OH– ® SnO32– + H2O
SnO2 + SnO32– ® SnO2 ![]() SnO32–
SnO32–
Electric Double Layer Theory or Helm-holtz Electric double layer :
The surface of colloid particles acquire a positive or negative charge by the selective (preferential) adsorptions of common ions carrying positive or negative charge respectively to form first layer. This layer attract counter ions from D.M. form a second layer. The combination of two layers of opposite charge around the colloidal particle is called Helm-holtz electric double layer. The first layer of ions is firmely held and is termed as fixed layer while the second layer is mobile which is termed as diffused layer. The charge of opposite ions of fixed and diffused layer double layer results in a difference in potential between two opposite charge layer is called the electrokinetic potential or zetapotential which can be given by
Example :
When silver nitrate solution is added to KI solution, the precipitation of AgI adsorb iodide ions from the D.M with the formation of fixed layer and negatively charged colloidal solution form, however when KI solution is added to AgNO3 solution positive charge sol result due to the adsorbs of Ag+ ions from D.M.
AgI/I– AgI/Ag+
Negative charged Positively charged.
This fixed layer attracts counter ions from the medium forming a second layer.
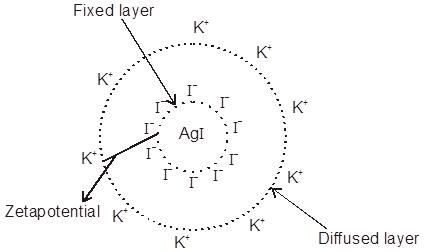
Coagulation/Flocculation : The presence of small amounts of appropriate electrolytes is necessary for the stability of the colloids. However, when an electrolyte is added in larger concentration; the particles of the sol take up the ions which are oppositely charged and thus get neutralised. The neutral particles then start aggregating giving particles of larger size which are then precipitated. This process of aggregation of colloidal particles into an insoluble precipitate by the addition of some suitable electrolyte is known as coagulation. At lower concentration of electrolytes, the aggregation of particles is called flocculation that can be reversed on shaking while at higher concentration of electrolyte, coagulation takes place and the same cannot be reversed simply by shaking. The stability of the lyophobic colloids is due to presence of charge on colloidal particles. If, somehow, the charge is removed, the particles will come near to each other to form aggregates and settled down under the force of gravity.
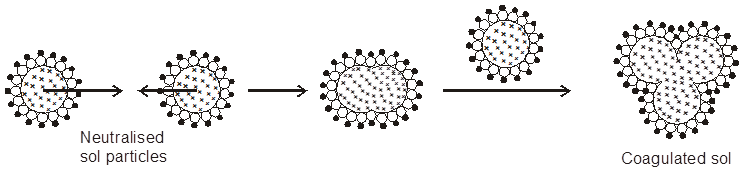
Coagulation of lyophobic sols can be carried out by the following methods.
(i) By electrophoresis
(ii) By mutual precipitation : It is a process in which oppositely charged sol are mixed in proper proportion to neutralise the charge of each other causing coagulation of both the sol.
Example : Positively charged Fe(OH)3 and negatively charged As2S3 colloidal particle containing sol on mixing get coagulated.
(iii) By Prolonged Dialysis : On prolonged dialysis, traces of the electrolyte present in the sol are removed almost completely and the colloidal unstable and ultimately coagulate.
(iv) By Boiling : Sols such as sulphur and silver halides dispersed in water may be coagulated by boiling because increased collisions between sol particle and the water molecule removed the adsorbed electrolytes. This takes away the charge from the particles and helps them to coagulate.
(v) By cooling : Certain sol can also be coagulated by lowering temperature. For example, accumulation of cream on the surface of milk on cooling. This is because at lower temperature the dispersion medium molecules do not exert sufficient force on to the dispersed particles and hence the Brownian motion becomes less effective.
(vi) By the addition of electrolyte : When excess of an electrolyte is added, the colloidal particles are precipitated.
Coagulation value or Flocculation value : It needs to be noted that the coagulation of a colloidal solution by an electrolyte does not take place until the added electrolyte has certain minimum concentration in the solution. The minimum concentration of electrolyte in millimoles required to cause coagulation of one litre of colloidal solution is called coagulation value. It is express in terms of millimoles/litre.
Coagulation value = 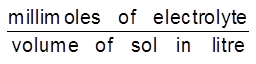
Comparision of relative coagulating power of two electrolyte for the same colloidal solution :
The coagulation value decrease with increase in charge of the coagulating ion.
Coagulating power µ ![]() .
.
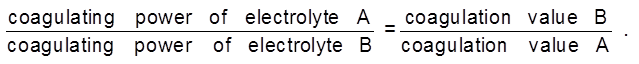
Hardy-Schulze Rule : According to this rule greater is the valency of coagulating ion, greater its power to cause precipitation. This is known as Hardy-Schulze.
In case of positive charged sol, the coagulating power of anion is in the order of [Fe(CN)6]4– > PO43– > SO42– > Cl–
In case of negative charged sol, the coagulating power of cation is in the order of Al3+ > Ba2+ > Na+.
The coagulating power of bivalent ion is 20-80 times higher than monovalent ion and coagulating power of trivalents is many times more than bivalent.
Protective colloidal sols : Lyophilic colloidal sols are much more stable than lyophobic colloidal sols. This is due to the extensive solvation of lyophilic colloidal sols, which forms a protective layer outside it and thus prevents it from forming associated colloids. Lyophobic sols can easily precipitate by addition of small amount of an electrolyte. They can be prevented from coagulation by previous addition of some lyophilic colloid. This is due to formation of a protective layer by lyophilic sols outside lyophobic sols. Process of protecting the lyophobic colloid solution from precipitation by an electrolyte due to previous addition of some lyophilic colloid is called protection of colloid and lyophilic colloidal sols are called protective sols.
Eg : Gelatin, Sodium caseinate, Egg albumin, Gum arabic, Potato starch etc.,
Gelatin (lyophilic) protects gold sol (lyophobic) colloids is expressed in terms of gold number.
Gold Number : Zpsigmondy (1901) introduce a term called gold number it is defined as ‘’the minimum amount of the protective colloid in milligrams which when added to 10 ml of a standard gold sol is just sufficient to prevent a colour change from red to blue on the addition of 1 ml of 10% sodium chloride solution. It may be noted that smaller of the gold number, greater will be protecting power of the protective colloid.
Protecting power µ . 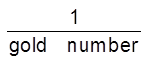
Gold Number = 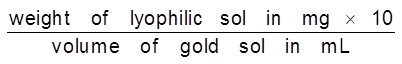
The gold numbers of a few protective colloids are as follows :
![]()
Uses of protective action :
(i) Gelatin is added in the preparation of ice cream to protect the particle of ice.
(ii) Protargol and Argyrol, is a silver sol protected by organic material used as eye drop.
Applications of Colloids : Colloids including emulsions find a number of uses in our daily life and industry. Some of the uses are given below.
n medicines : A wide variety of medicinal and pharmaceutical preparations are emulsions. Colloidial medicines are easily adsorbed by the body tissue because of large surface area.
* Colloidal antimony is used in curing kalaazar.
* Milk of magnesia, an emulsion, is used for stomach disorder.
* Colloidal gold is used for intramuscular injection.
* Colloidal sulphur are used as Germicides.
* Argyrol is a silver sol used as an eye lotion.
* Colloidal Fe(OH)3 is given to arsenic poisoning patients as it adsorbs arsenic and then gets omited out.
Tanning : Animal hides are colloidal in nature. Which contain positive charge colloidal particles of protein. This hide is kept in a tank containing tannic acid, which contains negatively charge colloidal particle. Therefore, mutual coagulation takes place this results in hardening of leather, this process is termed as tanning of leather. Chromium salts are also used in place of tannic acid.
Photographic plate & Film : Photographic plate or films are prepared by coating an emulsion of the light sensitive silver bromide in gelatin over glass plates or celluloid films. Gelatin prevent the coagulation of colloidal particle of AgBr.
Rubber plating : The negatively charged rubber particles from rubber sol are deposited on wares and handles of different tools. Rubber gloves are formed by rubber plating on suitable templates.
Sewage disposal : Sewage water contains charged colloidal particles of dirt, rubbish, etc., and these do not settle down easily. The particles can be removed by discharging them at electrodes. Dirty water is passed through a tunnel fitted with metallic electrodes which are maintained at high potential difference. The particles migrate to the oppositely charged electrode, lose their charge and get coagulated. The deposited matter is used as a manure and the water left behind is used for irrigation.
Cottrell smoke precipitator :Smoke is a dispersion of negatively charged colloidal particles of carbon in air and can be made free of these colloidal particles by passing it through cottrell precipitator as shown in fig. installed in the chimney of an industrial plant. It consists of two metal discs charged to a high potential. The carbon particles get discharged and precipitate, while gases come out from the chimney.
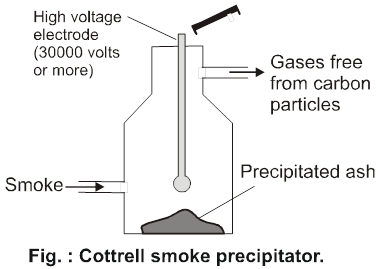
Formation of deltas : The river water contains colloidal particles of sand and clay which carry negative charge. The sea water contains +ve ions such as Na+, Mg2+, Ca2+, etc. As the river water meets sea water, these ions discharge the sand or clay particle which are precipitated in the form of delta.
Artificial rain : Cloud consists of charge particle of water disperse in air. Rain is caused by aggregation of these minute particles, artificial rain can be done by throwing electrified sand or Agl from aeroplanes, colloidal H2O particle present in cloud will get coagulated by these sand or Agl particles to form bigger water drops causing rain.
Stop bleeding from a cut : Blood is a colloidal solution containing a –ve charge colloidal particle (Albuminoid), bleeding can be stopped by use of alum or FeCl3 solution. The addition of Al3+ or Fe3+ causes coagulation of blood, so bleeding stops.
5. Emulsions
- Books Name
- ACME SMART COACHING Chemistry Book
- Publication
- ACME SMART PUBLICATION
- Course
- CBSE Class 12
- Subject
- Chemistry
EMULSIONS
Pair of immiscible liquid is called emulsion. Emulsion are unstable and some time they are separated into two layers on keeping still, for the stabilising of an emulsion, a third component is added called emulsifying-Agent form an interfacial film between D.P. and D.M.
Emulsion droplets are bigger than sol particles and can be seen under an ordinary microscope and sometimes even with a magnifying glass.
Example : Milk is an emulsion in which liquid fat is D.P. and liquid water is D.M. and casein is emulsifying agent.
Demulsification : The separation of an emulsion into its constituent liquids is called demulsification. Various techniques employed for this are freezing, boiling, centrifugation, electrostatic precipitation or chemical methods which destroys the emulsifying agents.
Demulsification can be brought about by :
(i) Freezing
(ii) Heating
(iii) Centrifugal action (Separation of cream of milk done by centrifugation).
(iv) Removal of emulsifiers by adding a better solvent for them like alcohol, phenol etc, called demulsifiers.
Types of emulsions : Depending on the nature of the dispersed phase, the emulsions are classified as :
(a) Oil in water emulsions
(b) Water in oil emulsions
(a) Oil in water emulsions (o/w) : This type of emulsions is formed when oil D.P. and water D.M.
Ex. :- Milk and vanishing cream are oil - in - water type emulsions.
(b) Water in oil emulsions (w/o) : This type of emulsions is formed when water is D.P. and oil is D.M.
Ex. : - Cold cream and cod liver oil.
[B] Applications of emulsions :
Disinfactants like phenyl, dettol when mixed with water form emulsion.
Digestion of fat in small intestine occurs easily due to emulsion.
In metallurgical process the concentration of ore by froath floatation method is based upon emulsion.
Milk is an emulsion of liquid fat in water in which casein emulsifying agent.
Cleansing action of soap is due to formation of emulsions. Soaps and detergents emulsify the grease along with the adhering dirt and carry them away in the wash water.
For concentrating ores, the finely powdered ore is treated with an oil. Oil forms emulsion with the ore particles. When air is bubbled into the mixture, emulsion containing the particles of the mineral are carried to the surface.
2. Metallurgy of Some Important Metals
- Books Name
- ACME SMART COACHING Chemistry Book
- Publication
- ACME SMART PUBLICATION
- Course
- CBSE Class 12
- Subject
- Chemistry
Metallurgy of Some Important Metals
1. Extraction of iron (Fe)
Ore: Haematite
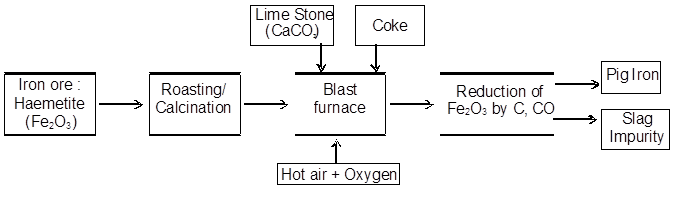
Oxide ores of iron, after concentration through calcination / roasting in reverberatory furnace (to remove water, to decompose carbonates and to oxidise sulphides) are mixed with lime stone and coke and fed into a Blast furnace from its top with the help of a cup and cone arrangement. Here, the oxide is reduced to the metal.
Thermodynamics helps us to understand how coke reduces the oxide and why this furnace is chosen. One of the main reduction steps in this process is :
FeO(s) + C(s) ® Fe(s/l) + CO (g) ........ (11)
It can be seen as a couple of two simpler reactions. In one, the reduction of FeO is taking place and in the other, C is being oxidised to CO :
FeO(s) ® Fe(s) + ![]() O2 (g) [DG(FeO, Fe) ] .............. (12)
O2 (g) [DG(FeO, Fe) ] .............. (12)
C(s) + ![]() O2 (g) ® CO (g) [DG(C, CO) ] .............. (13)
O2 (g) ® CO (g) [DG(C, CO) ] .............. (13)
When both the reactions take place to yield the equation (10), the net Gibbs energy change becomes:
D G (C,CO) + D G (FeO, Fe) = DrG .............. (14)
Naturally, the resultant reaction will take place when the right hand side in equation (14) is negative. In D G0 vs T plot representing reaction (12), the plot goes upward and that representing the change C CO (C,CO) goes downward. At temperatures above 1073K (approx.), the C,CO line comes below the Fe,FeO line
[DG(C, CO) < DG(Fe, FeO)]. So in this range, coke will be reducing the FeO and will itself be oxidised to CO. In a similar way the reduction of Fe3O4 and Fe2O3 at relatively lower temperatures by CO can be explained on the basis of lower lying points of intersection of their curves with the CO, CO2 curve in the given figure.
In the Blast furnace, reduction of iron oxides takes place in different temperature ranges. Hot air is blown from the bottom of the furnace and coke is burnt to give temperature upto about 2200K in the lower portion itself. The burning of coke therefore supplies most of the heat required in the process. The CO and heat moves to upper part of the furnace. In upper part, the temperature is lower and the iron oxides (Fe2O3 and Fe3O4) coming from the top are reduced in steps to FeO.
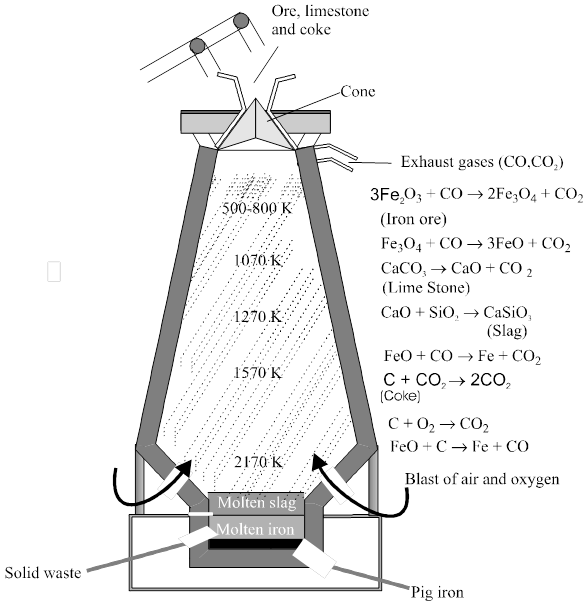
Reactions involved : The reactions proceed in several stages at different temperatures. Since the air passes through in a few seconds, the individual reactions does not reach equilibrium.
At 500 – 800 K (lower temperature range in the blast furnace)
3 Fe2O3 + CO®2 Fe3O4 + CO2
Fe3O4 + CO ® 3Fe + 4 CO2
Fe2O3 + CO ® 2FeO + CO2
At 900 – 1500 K (higher temperature range in the blast furnace):
C + CO2 ® 2 CO
FeO + CO ® Fe + CO2
Limestone is also decomposed tom CaO which removes silicate impurity of the ore as slag. The slag is in molten state and separates out from iron.
CaCO3 ® CaO + CO2
CaO + SiO2 ® CaSiO3
Note :
(1) CaSiO3 is used in cement industry or used in making building material.
(2) Slag CaSiO3 is ligther than molten Iron, get collected above it and protect iron from oxidation.
Pig Iron : Iron obtained from blast furnance contain 4%C & smaller amount of impurities of S , P , Si , Mn.
Cast Iron : Made by melting pig iron with scarp iron & coke & blast of hot air is passed through the molten mass. Contain about 3% carbon.
Wrought Iron : Purest form of iron prepared from cast iron by oxidising impurities in a reverbertory furnance lined with haematite. It have carbon about 0.1 to 0.21%
Note : (1) In steel making pure O2 is poured into molten metal where all impurities are converted to oxides then forming slag (basic oxygen) .
(2) Steel making process, from iron is an oxidation process.
(3) In production of steel from haematite ore involve first reduction & oxidation chemical process.
2. Extraction of Copper
(i) From Cuprous oxide
Sulphide ore are roasted to give oxide.
2 Cu2S + 3O2 ® 2Cu2O + 2SO2
As Cu2O line in D G V/s T graph is almost at top. so it is easily reduce to metal by heating with coke.
Cu2O + C ® 2 Cu + CO
(ii) From Copper Glance/ Copper Pyrite [self reduction]
Ore + flux  Slag + copper matte
Slag + copper matte
[CuFeS2] FeSiO3 [Cu2S + FeS]
(i) 2 CuFeS2 + 4O2 ® Cu2S + 2FeO + 3SO2.
(ii) Cu2S + FeO + SiO2 ® FeSiO3 + Cu2S.
Fusible slag Matte
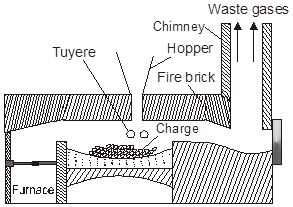
* Chemical composition of matte = (Mostly Cu2|S + some FeS)
2 FeS + 3O2 ® 2 Fe + 2 SO2 ,
FeO + SiO2 ® FeSiO3 [Slag]
Cu2S + 3O2 ® 2 Cu2O + 2 SO2
2 Cu2O + Cu2S ® 6 Cu + SO2 [Self Reduction ]
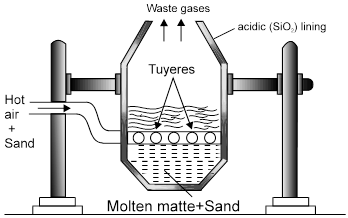
Note : Solidified copper has blistered appaerance due to evolution of SO2 so called as blister copper.
(iii) From Low Grade Ore
Þ From low grade ore , Cu is extracted by hydrometallurgy. (leaching)
(a) Low grade ore of Cu
Cu2O (Cuprite)
Cu2S [Copper glance] + ![]() CuSO4
CuSO4
Cu(OH)2 . CuCO3 (Malachite)
(b) CuSO4 ![]() Cu
Cu
(i) Electrolysing or
(ii) Metal displacement with Fe
Electrolytic Refining [Cu is purified by electro refining]
Anode Þ impure Cu & cathode = pure Cu.
Electrolyte Þ aqueous solution of CuSO4 :
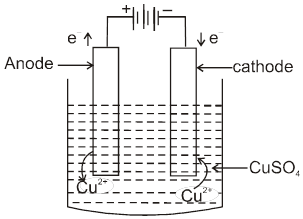
Anode Þ Cu(s) ® Cu2+(aq) + 2e–
Cathode Þ Cu2+(aq) + 2e ®Cu(s)
Anode Mud Þ Ag , Au , Pt.
3. Extraction of lead :
Ore: PbS (Lead sulphide)
There are two methods of extracting the element :
(i) Roast in air to give PbO, and then reduce with coke or CO in a blast furnace.
2PbS(s) + 3O2 (g) ![]() 2PbO (s)
2PbO (s) 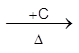 2Pb(l) + CO2 (g)
2Pb(l) + CO2 (g)
(ii) PbS is partially oxidized by heating and blowing air through it. After some time the air is turned off and heating is continued. The mixture undergoes self reduction as given below.
3PbS(s) 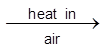 PbS (s) + 2PbO (s)
PbS (s) + 2PbO (s) ![]() 3Pb(l) + SO2 (g)
3Pb(l) + SO2 (g)
Chart3:

4. Extraction of zinc :
Ore: ZnS (Zinc blende)
The ore is roasted in presence of excess of air at temperature 1200 K.
2 ZnS + 3O2 ® 2 ZnO + 2SO2
The reduction of zinc oxide is done using coke. The temperature in this case is higher than that in case of copper. For the purpose of heating, the oxide is made into brickettes with coke and clay.
ZnO + C ![]() Zn + CO
Zn + CO
The metal is distilled off and collected by rapid chilling.
Note :
ZnO may be reduced by carbon monoxide at 1473 K (i.e. 1200°C) in smelter. The reaction is reversible, and the high temperature is required to move the equilibrium to the right. At this temperature the Zn is gaseous. If the gaseous mixture of Zn and CO2 was simply removed fom the furnace and cooled, then reoxidation of Zn would occur. Thus the zinc powder obtained would contain large amounts of ZnO.
ZnO + CO ![]() Zn + CO2
Zn + CO2
Chart4 :
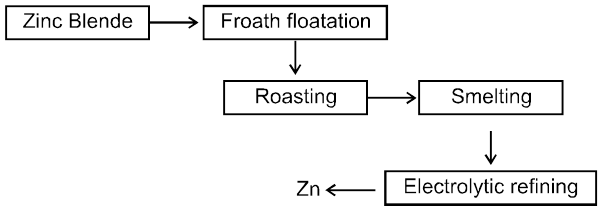
5. Extraction of tin from cassiterite (SnO2)
(i) Washing with water Þ To remove silicious impurities.
(ii) Electromagnetic sepration Þ To remove magnetic impurity of wolframite.
(iii) Roasting
(a) To remove volatile impurities S as SO2 As as AS2O3 and Sb as Sb2O3.
(b) ore contain impurites of CuS & FeS which are converted to their sulphate
CuS + 2O2 ¾® CuSO4, FeS + 2O2 ¾®FeSO4
(iv) Leaching ® CuSO & FeSO4 dissolve in water.
(v) Washing ® Ore is washed with running water. obtained orecontain 60-70% SnO2 & called as Black Tin.
(vi) Smelting : SnO2 is reduced by Carbon.
Product contain traces of Fe which is removed by passing air through molten mixture.
SnO2 + C ¾® Sn + CO
2Fe + O2 ¾®2FeO
Chart5:
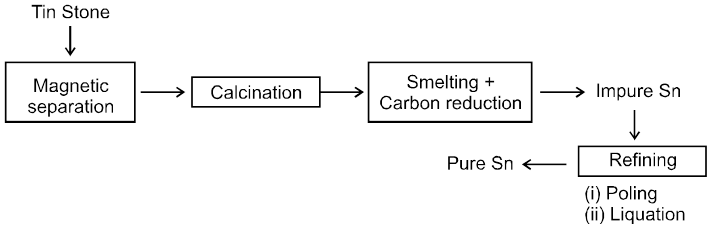
6. Extraction of Magnesium :
(i) From Carnallite :
The ore is dehydrated in a current of hydrogen chloride and the mixture of fused chlorides is electrolysed.
(ii) From Sea water (Dow’s process) :
Sea water contains 0.13% magnesium as chloride and sulphate. It involves following steps.
(a) Precipitation of magnesium as magnesium hydroxide by slaked lime :
MgCl2 + Ca(OH)2 ® Mg(OH)2![]() + CaCl2
+ CaCl2
(b) Preparation of hexahydrated magnesium chloride :
Mg(OH)2 + 2HCl(aq) ® MgCl2 + 2H2O
The solution on concentration and crystallisation gives the crystals of MgCl2.6H2O
(c) Preparation of anhydrous magnesium chloride :
MgCl2. 6H2O ![]() MgCl2 + 6H2O
MgCl2 + 6H2O
It is not made anhydrous by simple heating because it gets hydrolysed
MgCl2. 6H2O ![]() MgO + 5H2O + 2HCl
MgO + 5H2O + 2HCl
(d) Electrolysis of fused anhydrous MgCl2 :
Magnesium chloride obtained by any of the above methods is fused and mixed with sodium chloride and calcium chloride in the temperature range of 973 – 1023 K. The molten mixture is electrolysed. Magnesium is liberated at the cathode (iron pot) and chlorine is evolved at graphite anode.
MgCl2 ![]() Mg2+ + 2Cl–
Mg2+ + 2Cl–

At cathode : Mg2+ + 2e– ® Mg(99% pure) ;
At anode : 2Cl–® Cl2 + 2e–
A stream of coal gas is passed through the pot to prevent oxidation of magnesium metal. The magnesium obtained in liquid state is purified by distillation under reduced pressure.
(1 mm of Hg at 873 K).
7. Extraction of gold and silver (MacArthur-Forrest cyanide process) :
Chart6 :
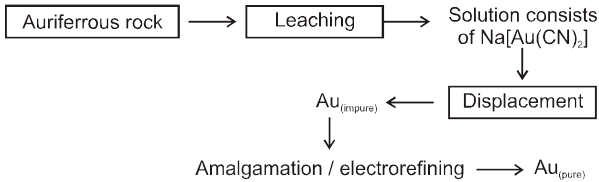
Chart7:
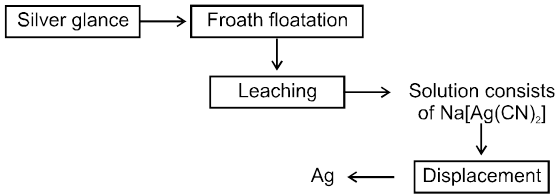
8. Extraction of Gold & Silver
MacArthur-forrest Cyanide process
(A) From native ore :
(i) Complex formation with CN¯ in presence of air
Ag + CN¯ + O2 ¾® [Ag(CN)2]¯(aq)
In this process, air is used which oxidises metal M(Ag/Au) to M+(Ag+/Au+) which form complex with CN¯ ion.
(ii) Metal displacement with Zn
[Ag(CN)2]¯ + Zn ¾® [Zn(CN)4]2–(aq) + Ag(s)
This is leaching (Hydro Meltallurgy) process.
(B) From Argentite ore
Extraction of Ag from Argentite ore by dissolving in NaCN and then using metal displacement is leaching process,which is an example of hydrometallurgy.
Ag2S (conc. ore) + 2 NaCN ![]() 2AgCN + Na2S
2AgCN + Na2S
Role of air : As Ag2S & AgCN are in equilibrium , air oxidise
Na2S to Na2SO4 & shift the equilibrium right.
4 Na2S + 5O2 + 2H2O ® 2Na2SO4 + 4 NaOH + 2S
AgCN + NaCN ® Na [Ag(CN)2] " soluble complex "
2 Na [Ag(CN)2] + Zn [dust] ® 2 Ag + Na [Zn (CN)4]
9. Extraction of Mercury
Chart8:
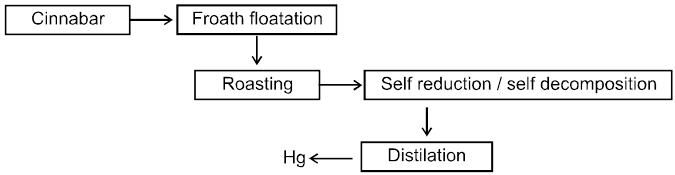
3. Purification or Refining of Metal
- Books Name
- ACME SMART COACHING Chemistry Book
- Publication
- ACME SMART PUBLICATION
- Course
- CBSE Class 12
- Subject
- Chemistry
Purification or Refining of Metal
Physical Method :
(1) Liquiation Process :
Based on difference in melting point of metal and impurity. This process is used for purification of those metal which have low melting point than each of impurities associated with metal.
Used for Purification of
(i) Impure tin metal (ii) Impure zinc (spelter)
Spelter Þ 97 % to 98 % zinc is known as spelter.
(iii) For removing Pb from Zn – Ag alloy.
(2) Fractional Distillation process
Used for purifying those metal which are easily volatile, while impurities present in it are not used for purifying Zn , Cd & Hg.
(3) Zone refining of metal
Principle : Based on principle that an impure molten metal on gradually celling will deposit crystal of pure metal while the impurity will be left in the remaining part of molten metal.
*This method is used when metal is required in very high purity.
Mainly used for purification of Si & Ge.
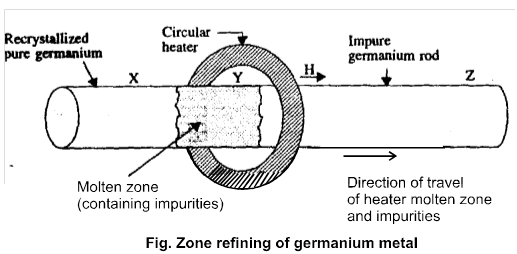
Note : High purity of metal can be obtained by zone refing method , if impurities have lower melting point.
(4) Chromatographic method
Principle : Based on the principle of adsorption.
*Different component of a mixture are differently adsorbed on an adsorbent.
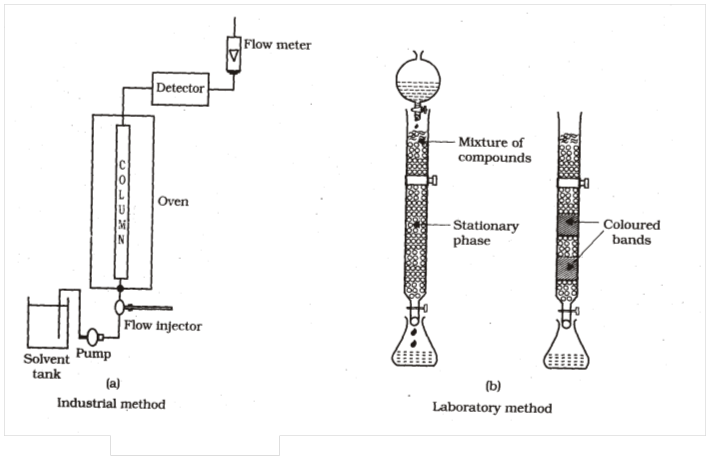
Chemical Method
(1) Oxidative Refining
Used when impurities present in metal are easily oxidised by oxygen.
Mainly used for refining Þ Pb , Ag , Cu , Fe .....
In this method , molten impure metal is subjected to oxidation.
(i) Bessemerisation [Purification of Iron]
Mainly used for manufacture of steel from cast iron.
Haematite ore  pig iron
pig iron 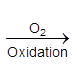 steel
steel
P is also oxidise to P4O10
P4 (l) + 5O2 ® P4O10 (l)
6 CaO (g) + P4O10 (l) ® 2 Ca3 (PO4)2 (l)
Thomas Slag
Which is used as fertilizer.
(ii) Cupellation (Removal of lead)
Mainly used to remove Pb from Ag or Au.
(2) Poling Process
This method is used for purification of those impure metal which contain their own oxide as one of the impurities.
Eg. (a) Purification of Cu.(b) Purification of impure Tin.
(3) Electrolytic refining
Metal , Cu , Ni & Al refined electrolytically.
The anode mud obtained in the electrolytic refining has
Electrolytic refining Anode Mud
(i) Lead Ag , Au , Sb , Cu.
(ii) Cu Ag , Au , Pt.
(iii) Ag Au , Pt.
(4) (a) Kroll's Process Þ For Ti & Zr.
TiCl4 + 2 Mg ![]() Ti + 2MgCl2
Ti + 2MgCl2
(b) IMI process Þ [ Imperial Metal industries ]
TiCl4 + 4 Na  Ti + 4 NaCl.
Ti + 4 NaCl.
Vapour phase refining :
(a) Extraction of Nickel [ Mond's Process ]
Used for purification (refining) of Ni.
Ni form complex with Co , [Ni(CO)4] which volatilized
[BP=43°] & then decompose at 200°C in Ni & CO.
Ni(S) + 4 CO ![]() Ni (CO)4(g)
Ni (CO)4(g) ![]() Ni + 4 CO.
Ni + 4 CO.
readily volatile
(B.P. = 43°C)
(b) VanArkel – DeBoer Process
Used for purification of Ti , Zr , Bi & B.
Small amount of puremetal is obtained.
Impure Ti(S) + 2I2 ![]() TiI4(g)
TiI4(g) ![]() Ti + 2I2
Ti + 2I2
KROLL’S PROCESS :
TiCI4 + 2 Mg ![]() Ti + 2 MgCI2 (Kroll’s process)
Ti + 2 MgCI2 (Kroll’s process)
TiCI4 + 4 Na  Ti + 4 NaCI (Imperial metal industries (IMI) process)
Ti + 4 NaCI (Imperial metal industries (IMI) process)
NaCI is leached with H2O. Ti is in the form of small granules. These can be fabricated into metal parts using “powder forming” techniques and sintering in an inert atmosphere. Zr is also produced by Kroll’s process.
VAPOR PHASE REFINING :
(i) Extraction of Nickel (Mond’s process) :
Nickel is extracted from sulfide ore by roasting followed by reduction with carbon, but the process is complicated by the fact that nickel is found in association with other metals. The refining is rather unusual, for nickel forms a complex with carbon monoxide tetracarbonylnickel (O) [Ni(CO)4]. This substance is molecular in molecular in structure and readily volatilized (boiling point 43ºC). It is made by heating nickel powder to 50ºC, in a stream of CO and then decomposed at 200ºC. Any impurity in the nickel sample remains in the solid state and the gas is heated to 230ºC, when it decomposes, giving pure metal and CO, which is recycled. Ni(CO)4 is gaseous and may be produced by warming nickel with CO at 50ºC.
The sequence of reaction is
H2O(g) + C ® CO(g) + H2
Ni(s) + 4 CO(s) ![]() [Ni(CO4)] (g)
[Ni(CO4)] (g)
[Ni (CO)4](g) ![]() Ni + 4CO(g)
Ni + 4CO(g)
(ii) Van Arkel–De Boer process :
Small amounts of very pure metals (Ti, Zr, or Bi) can be produced by this method. This process is based on the fact that iodides are the least stable of the halides. The impure element is heated with iodine, producing a volatile iodide, TiI4, ZrI4, or BiI3. These are decomposed by passing the gas over an electrically heated filament of tungsten or tantalum that is white hot. The element is deposited on the filament and the iodine is recycled. As more metal is deposited on the filament, it conducts electricity better. Thus, more electric current must be passed to keep it white hot. Thus the filament grows fatter and eventually the metal is recovered. The tungsten core is distilled out of the center and a small amount of high purity metal is obtained.
Impure ![]()
The method is very expensive and is employed for the preparation of very pure metal for specific use.
(iii) Parke’s process :
The removal of the impurities of Ag from the commercial lead is called desilverisation of lead and is done by Parke’s process . Thus, Parke’s process is the desilverisation of lead.
In Parke’s process, the commercial lead, which contains Ag as impurities, is melted in iron pots and 1% of Zn is added to it. The molten mass is thoroughly agitated. Since Ag is about 300 times more soluble in Zn than in Pb, most of the Ag present in the commercial lead as impurity mixes with Zn, to form Zn–Ag alloy. When the whole is cooled, two layers are obtained. The upper layer contains Zn–Ag alloy in the solid state, while the lower layer has lead in the molten state. This lead contains only 0.0004% of Ag and hence is almost pure. Lead obtained after removing most of Ag from it (desilverisation of lead) by Parke’s process, is called desilverised lead. This lead contains the impurities of metals like Zn, Au, Sb etc. These metal impurities are removed from desilverised lead by Bett’s electrolytic process.
Zn–Ag alloy, formed in the upper layer, is skimmed off from the surface of the molten lead by perforate ladles. This alloy contains lead as impurity. This impurity of Pb is removed from the alloy by liquation process, in which Zn–Ag alloy is heated in a slopping furnace, when the impurity of Pb melts and hence drains away from the solid alloy. Thus purified Zn–Ag is obtained. Now Ag can be obtained from this purified Zn–Ag alloy by distillation process, in which the alloy is heated strongly in presence of little carbon in a fire–clay retort. Zn, being more volatile, distills off while Ag remains in the retort, carbon used in the process reuses the oxide of Zn, if formed. Ag obtained from Zn–Ag alloy is contaminated with a little of Pb as impurity. This impurity of Pb placed in a cupel (cupel is a boat–shaped) dish made of bone ash which is porous in nature) in a reverberatory furnace and heated in the presence of air. By doing so, lead (impurity) is oxidised to PbO(litharge) which volatilises and pure Ag is left behind in the cupel. Last traces of PbO are absorbed by the porous mass of the cupel.
(iv) Pudding process : This process is used for the manufacture of wrought iron from cast iron. We know that cast iron contains the impurities of C, S, Si, Mn and P. When these impurities are removed from cast iron, we get wrought iron. In this process the impurities are oxidised to theiro xides not by blast of air but by the haematite (Fe2O3) lining of the furnace.
1. Group 15 elements
- Books Name
- ACME SMART COACHING Chemistry Book
- Publication
- ACME SMART PUBLICATION
- Course
- CBSE Class 12
- Subject
- Chemistry
Chapter 7
p-block (nitrogen and oxygen family)
Introduction :
Group 13 to 18 of the periodic table of elements constitute the p–block. The p–block contains metals, metalloids as well as non–metals.
The p–block elements have general valence shell electronic configuration ns2 np1–6.
The first member of each group from 13–17 of the p–block elements differ in many respects from the other members of their respective groups because of small size, high electronegativity and absence of d–orbitals.
The first member of a group also has greater ability to form pp–pp multiple bonds to itself (e.g. C=C, CºC, NºN) and to element of second row (e.g C=O, C=N, CºN, N=O) compared to the other members of the same group.
The highest oxidation of p–block element is equal to the group number minus 10. Moving down the group, the oxidation state two less than the highest group oxidation state becomes more stable in groups 13 to 16 due to inert pair effect (reluctance of s-subshell electrons to participate in chemical bonding)
Group 15 Elements : The Nitrogen family
Group 15 includes nitrogen phosphorus, arsenic, antimony and bismuth. As we go down the group, there is a shift from non-metallic to metallic through metalloidic character. Nitrogen and phosphorus are non-metal, arsenic and antimony metalloid and bismuth is a typical metal.
Electronic Configuration : The valence shell electronic configuration of these element is ns2 np3. The s orbital in these element is completely filled and p orbitals are half- filled, making their electronic configuration extra stable.
Atomic and Ionic Radii : Covalent and ionic (in a particular state) radii increase in size down the group. There is a considerable increase in covalent radius from N to P. However, from As to Bi only a small increase in covalent radius is observed. This is due to the presence of completely filled d and / or f orbitals in heavier members.
Ionisation Enthalpy : Ionisation enthalpy decreases down the group due to gradual increase in atomic size. Because of the extra stable half- filled p-orbital electronic configuration and smaller size, the ionisation enthalpy of the group 15 element is much greater than of group 14 elements in the corresponding periods. The order of successive ionisation enthalpies, as expected is DiH1 < DiH2 < DiH3
Electronegativity : The electronegativity value, in general, decreases down the group with increasing atomic size. However, amongst the heavier elements, the difference is not that much pronounced.
Physical Properties : All the elements of this group are polyatomic. Dinitrogen is a diatomic gas while all others are solids. Metallic character increases down the group. Nitrogen and phosphorus are non–metals, arsenic and antimony metalloids and bismuth is a metal. This is due to decrease in ionisation enthalpy and increase in atomic size. The boiling points, in general, increase from top to bottom in the group but the melting point increases upto arsenic and then decreases upto bismuth. Except nitrogen, all the elements show allotropy.
Atomic & physical properties
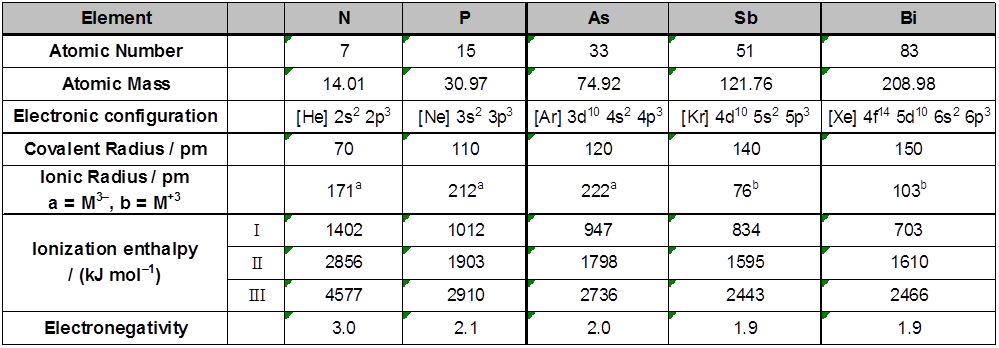
Chemical Properties :
Oxidation States and trends in a chemical reactivity :
The common oxidation states of these elements are –3, +3 and +5. The tendency to exhibit –3 oxidation state decreases down the group , bismuth hardly forms any compound in –3 oxidation state. The stability of +5 oxidation state decreases down the group. The only well characterised Bi (V) compound is BiF5 .The stability of +5 oxidation state decreases and that of +3 state increases (due to inert pair effect) down the group.
Bi3+ > Sb3+ > As3+ ; Bi5+ < Sb5+ < As5+
Nitrogen exhibits +1, +2, +4 oxidation states also when it reacts with oxygen. Phosphorus also shows +1 and +4 oxidation states in some oxoacids.
In the case of nitrogen, all oxidation states from +1 to +4 tend to disproportionate in acid solution.
For example,
3 HNO2 —® HNO3 + H2O + 2 NO
Similarly, in case of phosphorus nearly all intermediate oxidation states disproportionate into +5 and –3 both in alkali and acid. However +3 oxidation state in case of arsenic , antimony and bismuth become increasingly stable with respect to disproportionation.
Nitrogen is restricted to a maximum covalency of 4 since only four (one s and three p) orbitals are available for bonding. The heavier elements have vacant d orbitals in the outermost shell which can be used for bonding (covalency) and hence , expand their covalence as in PF6– .
Anomalous properties of nitrogen :
Nitrogen differs from the rest of the members of this group due to its smaller size, high electronegativity, high ionisation enthalpy and non–availability of d orbitals. Nitrogen has unique ability to form pp–pp multiple bonds with itself and with other elements having small size and high electronegativity (e.g., C, O). Heavier elements of this group do not form pp–pp bonds as their atomic orbitals are so large and diffuse that they cannot have effective overlapping. Thus, nitrogen exists as a diatomic molecule with a triple bond (one s and two p) between the two atoms. Consequently, its bond enthalpy (941.1 kJ mol–1) is very high. On the contrary, phosphorus, arsenic and antimony form metallic bonds in elemental state. However, the single N–N bond is weaker than the single P–P bond because of high interelectronic repulsion of the non–bonding electrons, owing to the small bond length. As a result the catenation tendency is weaker in nitrogen. Another factor which affects the chemistry of nitrogen is the absence of d orbitals in its valence shell. Besides restricting its covalency to four, nitrogen cannot form dp–pp bonds as the heavier elements can e.g., R3P=O or R3P=CH2 (R = alkyl group). Phosphorus and arsenic can form dp–pp bond also with transition metals when their compounds like P(C2H5)3 and As(C6H5)3 act as ligands.
(i) Reactivity towards hydrogen : All the elements of Group 15 form hydrides of the type EH3 where E=N, P, As, Sb or Bi. Some of the properties of these hydrides are shown in Table. The hydrides show regular gradation in their properties. The stability of hydrides decreases from NH3 to BiH3 which can be observed from their bond dissociation enthalpy. Consequently, the reducing character of the hydrides increases. Ammonia is only a mild reducing agent while BiH3 is the strongest reducing agent amongst all the hydrides. Basicity also decreases in the order NH3 > PH3 > AsH3 > SbH3 ³ BiH3 .
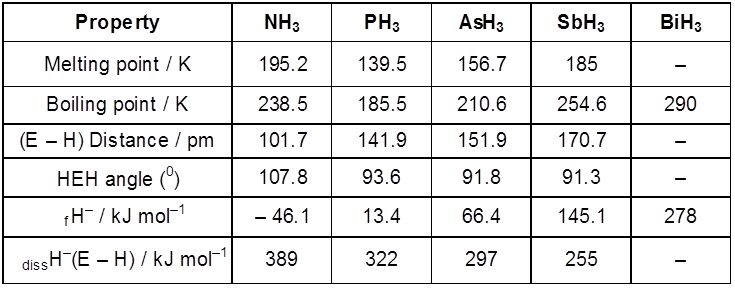
Properties of Hydrides of Group 15 Elements
(ii) Reactivity towards oxygen : All these elements form two types of oxides : E2O3 and E2O5 . The oxide in the higher oxidation state of the element is more acidic than that of lower oxidation state. Their acidic character decreases down the group. The oxides of the type E2O3 of nitrogen and phosphorus are purely acidic , that of arsenic and antimony amphoteric and those of bismuth is predominantly basic.
(iii) Reactivity towards halogens : These elements react to form two series of halides : EX3 and EX5 . Nitrogen does not form pentahalide due to non – availability of the d-orbitals in its valence shell. Pentahalides are more covalent than trihalides. All the trihalides of these elements except those of nitrogen are stable. In case of nitrogen, only NF3 is known to be stable. Trihalides except BiF3 are predominantly covalent in nature. Halides are hydrolysed in water forming oxyacids or oxychlorides.
PCl3 + H2O —® H3PO3 + HCl
SbCl3 + H2O —® SbOCl¯ (orange) + 2HCl
BiCl3 + H2O —® BiOCl¯ (white) + 2HCl
(iv) Reactivity towards metals : These elements react with metals to form their binary compounds exhibiting –3 oxidation state , such as , Ca3N2 (calcium nitride) Ca3P2 (calcium phosphide) , Na3As2 (sodium arsenide), Zn3Sb2 (zinc antimonide) and Mg3Bi2 (magnesium bismuthide).
1.Group 17 elements
- Books Name
- ACME SMART COACHING Chemistry Book
- Publication
- ACME SMART PUBLICATION
- Course
- CBSE Class 12
- Subject
- Chemistry
Chapter 8
p-block elements
(halogens family and noble gases)
Introduction :
Group 13 to 18 of the periodic table of elements constitute the p–block. The p–block contains metals, metalloids as well as non–metals.
The p–block elements have general valence shell electronic configuration ns2 np1–6.
The first member of each group from 13–17 of the p–block elements differ in many respects from the other members of their respective groups because of small size, high electronegativity and absence of d–orbitals.
The first member of a group also has greater ability to form pp–pp multiple bonds to itself (e.g. C=C, C=C, N º N) and to element of second row (e.g C=O, C=N, CºN, N=O) compared to the other members of the same group.
The highest oxidation of p–block element is equal to the group number minus 10. Moving down the group, the oxidation state two less than the highest group oxidation state becomes more stable in groups 13 to 16 due to inert pair effect (reluctance of s-subshell electrons to participate in chemical bonding)
Group 17 Elements : The Halogen Family
Electronic Configuration : All these elements have seven electrons in their outermost shell (ns2 np5) which is one electron short of the next noble gas.
Atomic and Ionic Radii : The halogens have the smallest atomic radii in their respective periods due to maximum effective nuclear charge . Atomic and ionic radii increase from fluorine to iodine due to increasing number of quantum shells.
Ionisation Enthalpy : They have little tendency to lose electron. Thus they have very high ionisation enthalpy. Due to increase in atomic size, ionisation enthalpy decreases down the group.
Electron Gain Enthalpy : Halogen have maximum negative electron gain enthalpy in the corresponding period. This is due to the fact that the atoms of these elements have only one electron less than stable noble gas configurations. Electron gain enthalpy of the elements of the group becomes less negative down the group. However, the negative electron gain enthalpy of fluorine is less than that of chlorine. It is due to small size of fluorine atom. As a result, there are strong interelectronic repulsions in the relatively small 2p orbitals of fluorine and thus, the extra electron (incoming) does not experience much attraction.
Electronegativity : They have very high electronegativity. The electronegativity decreases down the group. Fluorine is the most electronegative element in the periodic table
Physical Properties : Fluorine and chlorine are gases, bromine is a liquid whereas iodine is a solid. Their melting and boiling points steadily increase with atomic number. All halogens are coloured. This is due to absorption of radiations in visible region which results in the excitation of outer electrons to higher energy level. By absorbing different quanta of radiation, they display different colours. For example, F2, has yellow, Cl2, greenish yellow, Br2, red and I2, violet colour. Fluorine and chlorine react with water. Bromine and iodine are only sparingly soluble in water. But are soluble in organic solvents such as chloroform, carbon tetrachloride, carbon disulphide and hydrocarbons to give coloured solutions. Except the smaller enthalpy of dissociation of F2 compared to that of Cl2. The X-X bond disassociation enthalpies from chlorine onwards show the expected trend : Cl – Cl > Br – Br > F – F > I – I. The reason for the smaller enthalpy of dissociation of F2 is the relatively larger electrons-electrons repulsion among the lone pairs in F2 molecule where they are much closer to each other than in case of Cl2.
Atomic & physical properties
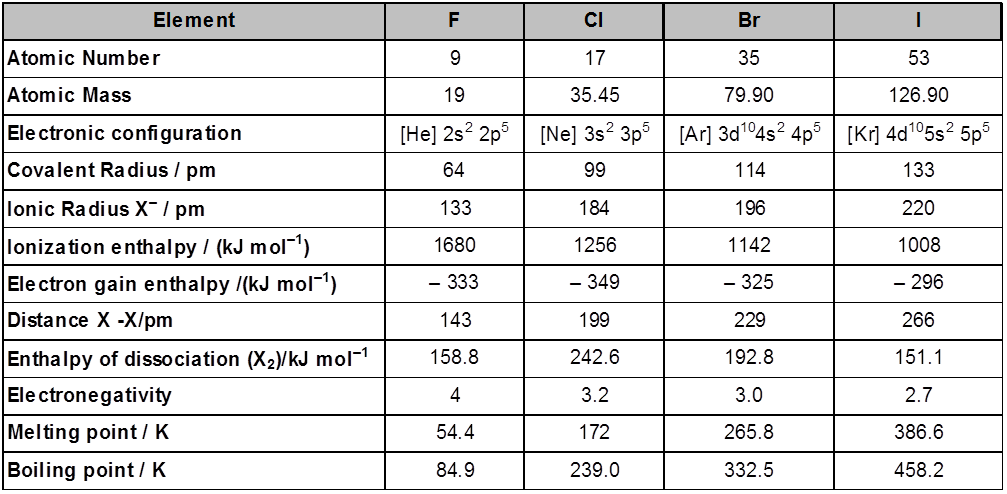
Chemical Properties
Oxidation states and trends in chemical reactivity
All the halogens exhibit –1 oxidation state. However, chlorine, bromine and iodine exhibit + 1, + 3, + 5 and + 7 oxidation states also. The higher oxidation states of chlorine, bromine and iodine are realised mainly when the halogens are in combination with the small and highly electronegative fluorine and oxygen atoms e.g., in interhalogens, oxides and oxoacids.
The fluorine atom has no d orbitals in its valence shell and therefore cannot expand its octet. Being the most electronegative, it exhibits only – 1 oxidation state.
All the halogens are highly reactive. They react with metals and non-metals to form halides. The reactivity of the halogens decreases down the group.
The ready acceptance of an electron is the reason for the strong oxidising nature of halogens. F2 is the strongest oxidising halogen and it oxidises other halide ions in solution or even in the solid phase. The decreasing oxidising ability of the halogens in aqueous solution down the group is evident from their standard electrode potentials. Fluorine oxidises water to oxygen whereas chlorine and bromine react with water to form corresponding hydrohalic and hypohalous acids. The reactions of iodine with water is non- spontaneous . I– can be oxidised by oxygen in acidic medium; just the reverse of the reaction observed with fluorine.
2F2(g) + 2H2O(l) ® 4H+ (aq) + 4F– (aq) + O2(g)
X2(g) + H2O (l) ® HX(aq) + HOX (aq) ; (where X = Cl or Br)
4I– (aq) + 4H+ (aq) + O2(g) ® 2 I2 (s) + 2H2O (l)
Standard Reduction Potential (SRP)
X2 + 2e– ® 2X–
F2 + 2e– ® 2F– [E° = + 2.87 V ]
Cl2 + 2e– ® 2Cl– [E° = + 1.36 V]
Br2 + 2e – ® 2Br – [E° = + 1.09 V ]
I2 + 2e– ® 2I– [E° = + 0.54 V]
More the value of the SRP, more powerful is the oxidising agent. Hence the order of oxidising power is
F2 > Cl2 > Br2 > I2
Since SRP is the highest for F2 (among all elements of periodic table), it is a strongest oxidising agent.
Hydration energy of X–
Smaller the ion, higher is the hydration energy.
F – Cl – Br – I–
515 381 347 305 in kJ/mol
Anomalous behaviour of fluorine
The anomalous behaviour of fluorine is due to its small size, highest electronegativity, low F- F bond dissociation enthalpy, and non availability of d orbitals in valence shell. Most of the reactions of fluorine are exothermic (due to the small and strong bond formed by it with other elements). It forms only one oxoacid while other halogens form a number of oxoacids. Hydrogen fluoride is liquid (b.p. 293 K) due to strong hydrogen bonding. Other hydrogen halides are gases.
(i) Reactivity towards hydrogen : They all react with hydrogen to give hydrogen halides but affinity for hydrogen decreases from fluorine to iodine with increasing atomic number. They dissolve in water to form hydrohalic acids. The acidic strength of these acids increases in the order : HF < HCl < HBr < HI. The stability of these halides decreases down the group due to decrease in bond (H–X) dissociation enthalpy in the order :
H – F > H – Cl > H –Br > H – I .
(ii) Reactivity towards oxygen : Halogens form many oxides with oxygen but most of them are unstable. Fluorine forms two oxides OF2 and O2F2. However, only OF2 is the thermally stable at 298 K. These oxide are essentially oxygen fluorides because of the higher electronegativity of flurorine than oxygen . Both are strong fluorinating agents. O2F2 oxidises plutonium to PuF6 and the reaction is used in removing plutonium as PuF6 from spent nuclear fuel.
Chlorine, bromine and iodine form oxides in which the oxidation states of these halogen vary from + 1 to + 7. A combination of kinetic and thermodynamic factors lead to the generally decreasing order of stability of oxides formed by halogens, I > Cl > Br. The higher oxides of halogens tend to be more stable than the lower ones.
Chlorine oxides, Cl2O, ClO2, Cl2O6 and Cl2O7 are highly reactive oxidising agents and tend to explode. ClO2 is used as a bleaching agent for paper pulp and textiles and in water treatment.
The bromine oxides, Br2O, BrO2, BrO3 are the least stable halogen oxides and exist only at low temperature. They are very powerful oxidising agents.
The iodine oxides, I2O4, I2O5, I2O7 are insoluble solids and decompose on heating. I2O5 is very good oxidising agent and is used in the estimation of carbon monoxide.
(iii) Reactivity towards metals : Halogen react with metals to form metal halides. For e.g., bromine reacts with magnesium to give magnesium bromide.
(iv) Reactivity of halogen towards other halogens : Halogens combine amongst themselves to form a number of compounds known as interhalogen of the types AB, AB3, AB5 and AB7 where A is a larger size halogen and B is smaller size halogen.
1. Periodic trends and properties of d-Block Elements
- Books Name
- ACME SMART COACHING Chemistry Book
- Publication
- ACME SMART PUBLICATION
- Course
- CBSE Class 12
- Subject
- Chemistry
Chapter 9: d & f Block
d & f-block elements & their important compounds

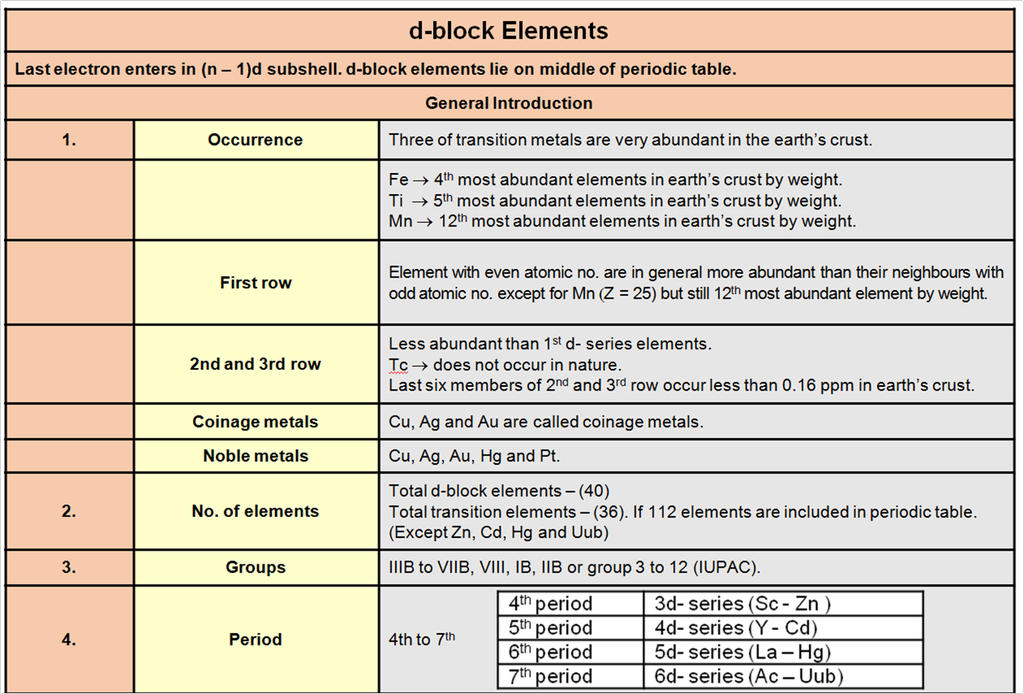
Periodic trends and chemical properties
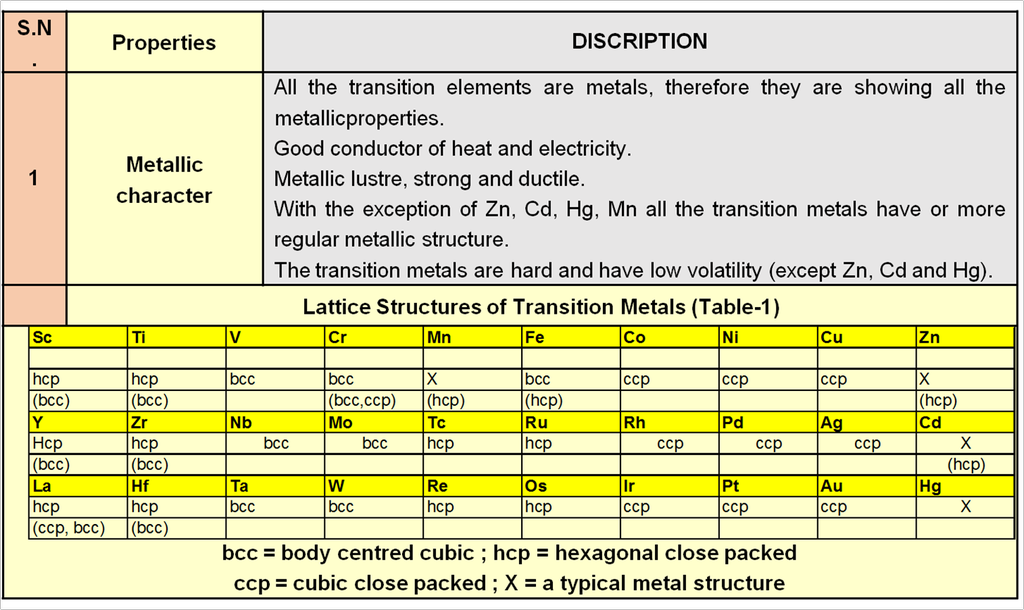
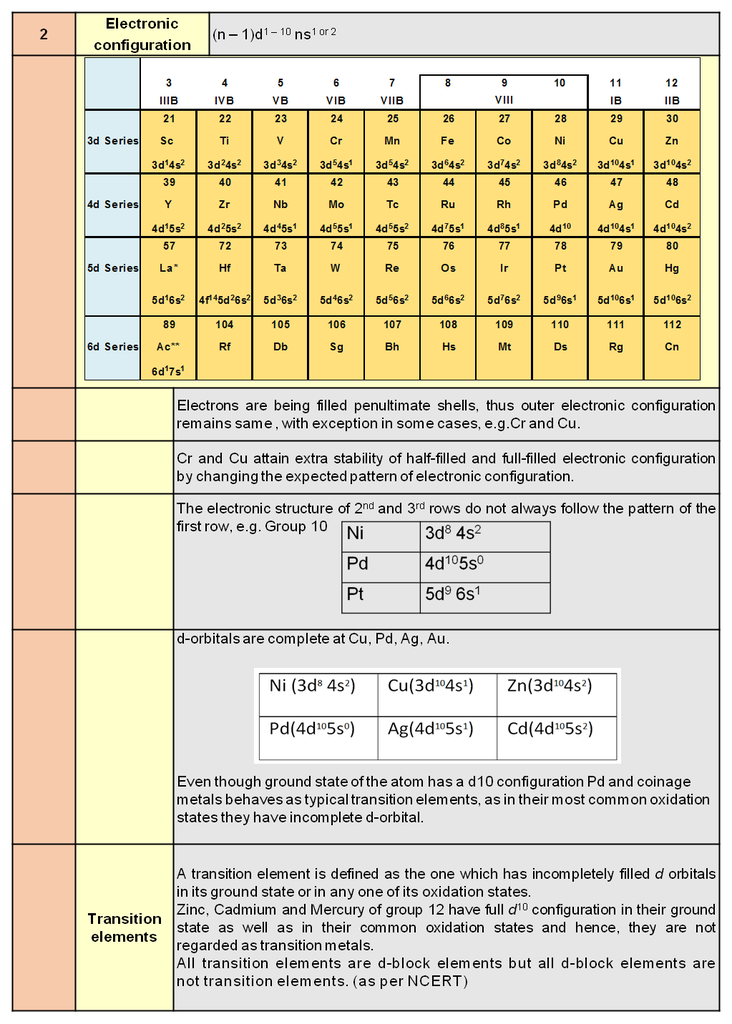
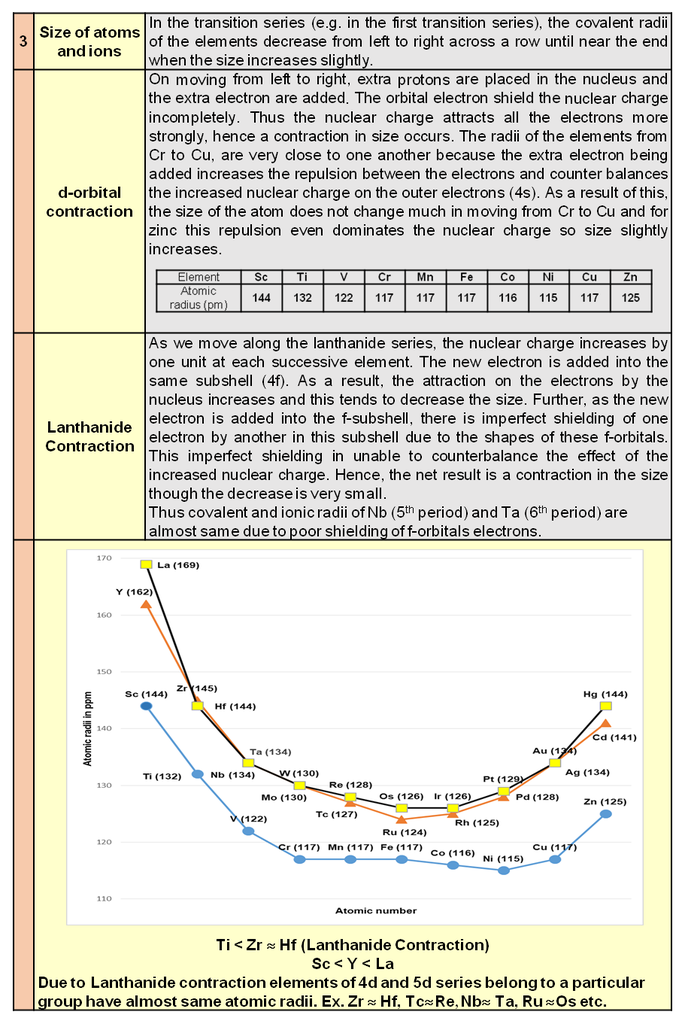
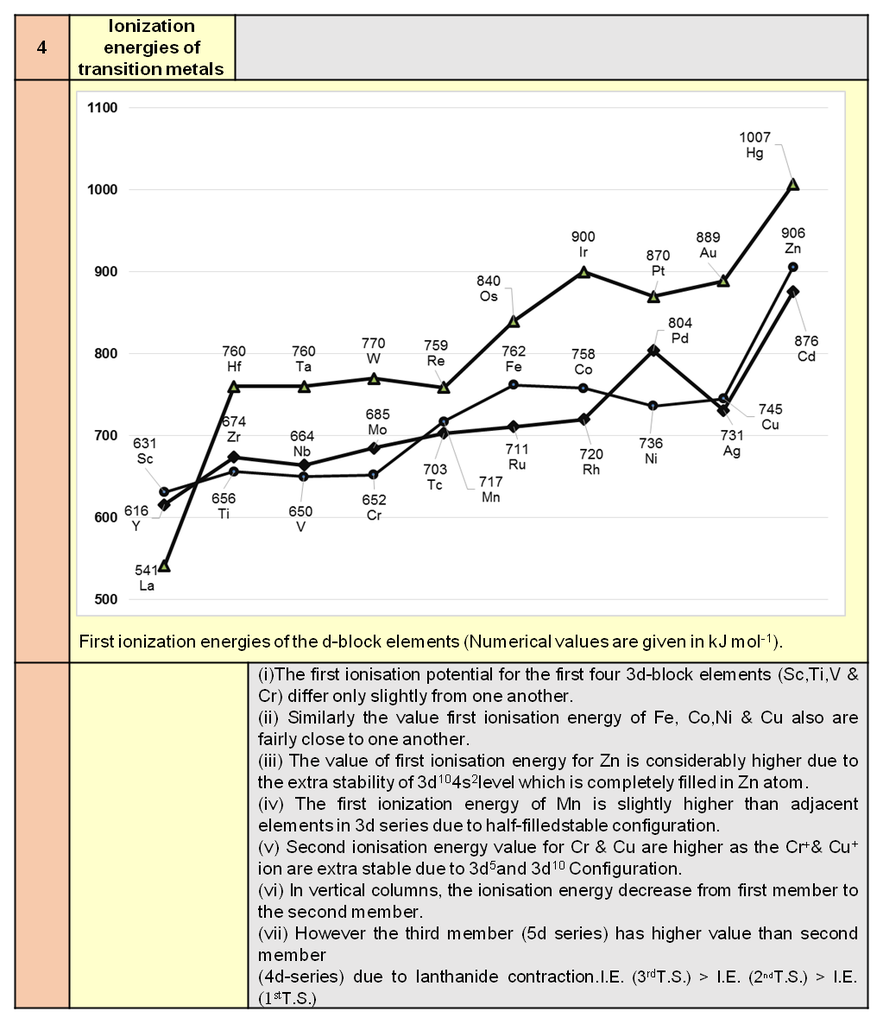
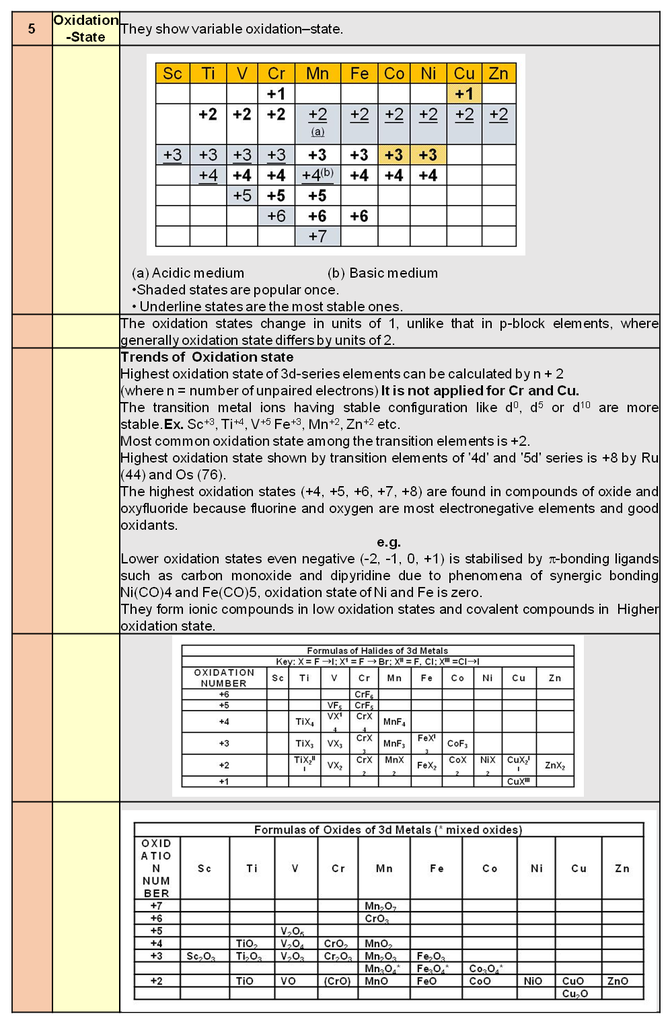
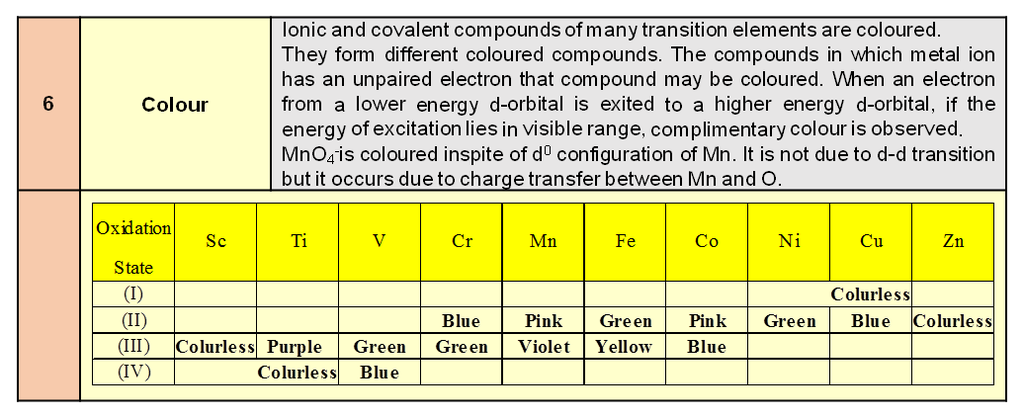
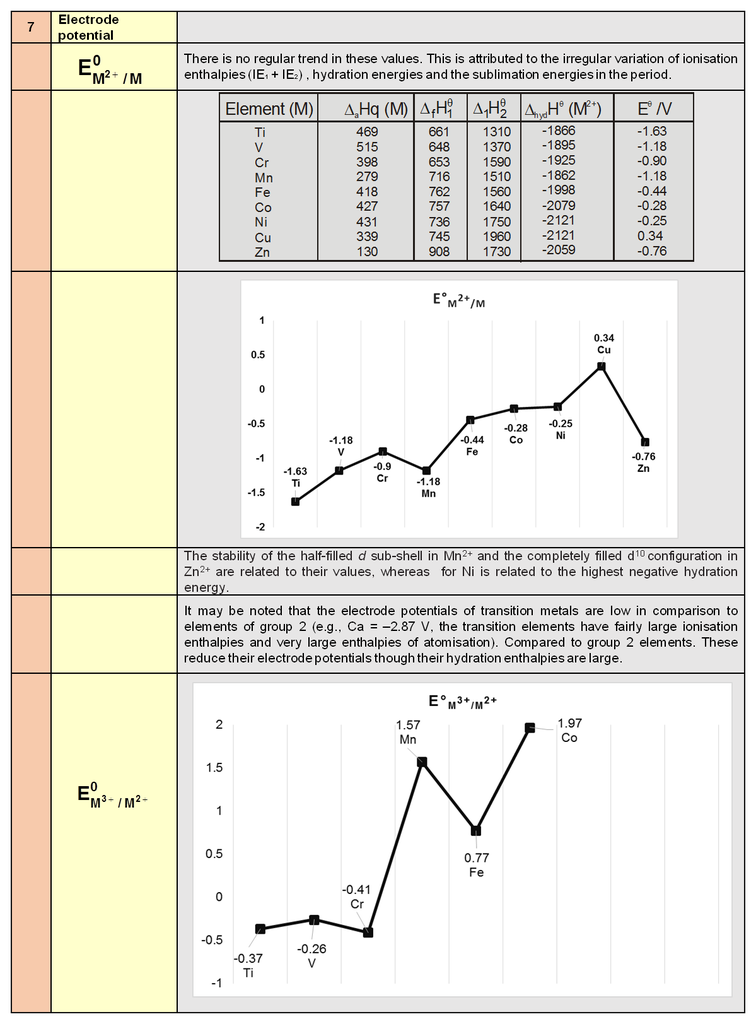
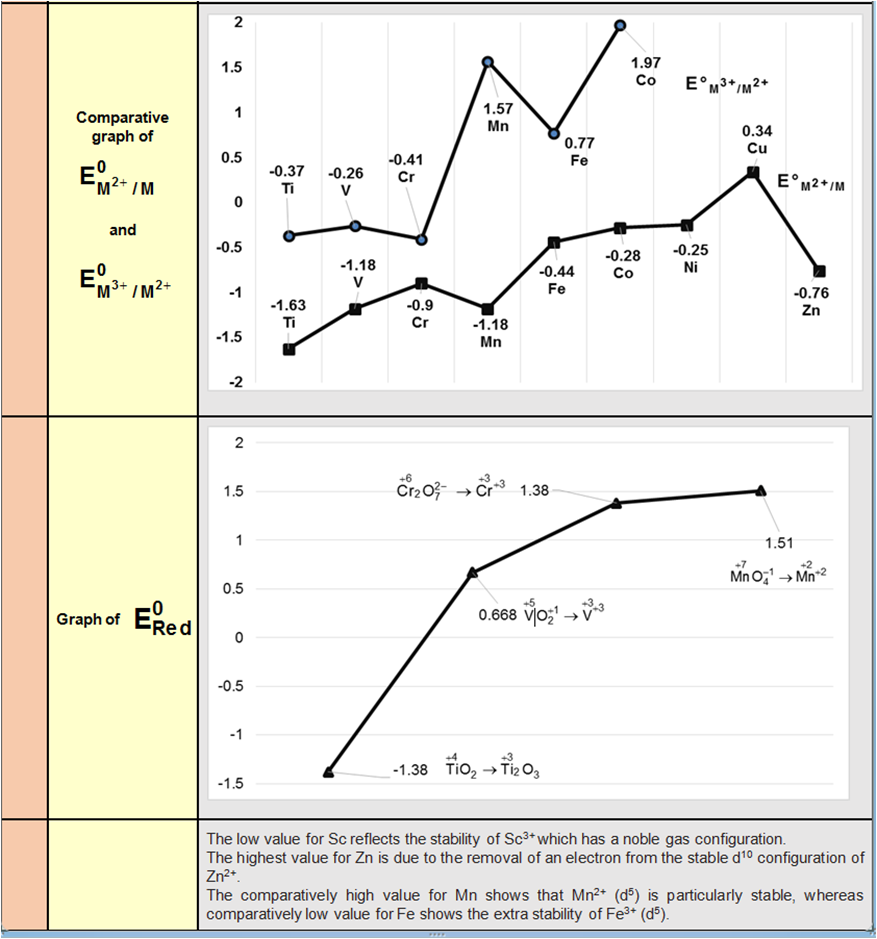
2. Dinitrogen
- Books Name
- ACME SMART COACHING Chemistry Book
- Publication
- ACME SMART PUBLICATION
- Course
- CBSE Class 12
- Subject
- Chemistry
DINITROGEN (N2)
Preparation :
(i) Laboratory method of preparation :
NH4Cl (aq) + NaNO2 —® (aq) N2 (g) + 2 H2O (1) + NaCl (aq)
Small amounts of NO and HNO3 are also formed in this reaction ; these impurities can be removed by passing the gas through aqueous suplhuric acid containing potassium dichromate.
N2 is collected by the downward displacement of water.
(ii) By heating ammonium dichromate : (NH4)2Cr2O7 ![]() N2↑ + 4H2O + Cr2O3
N2↑ + 4H2O + Cr2O3
(iii) Very pure nitrogen ; Ba(N3)2 Ba + 3N2
Sodium azide also gives N2 on heating.
(iv) Industrial method of preparation :
From liquefied air by fractional distillation : The boiling point of N2 is –196oC and that of oxygen is –183oC and hence they can be separated by distillation using fractional column.
Properties :
(i) N2 is a colourless, odourless, tastless, non-toxic gas having very low solubility in water (23.2 cm3 per litre water at 273 K and 1 bar pressure). It has two stable isotopes : 14N and 15N. It is neither combustible nor a supporter of combustion.
(ii) Li, Mg and Al on heating with N2 form corresponding nitrides.
6Li + N2 ![]() 2Li3N ; 3Mg + N2
2Li3N ; 3Mg + N2 ![]() Mg3N2 ; 2Al + N2
Mg3N2 ; 2Al + N2![]() 2AlN
2AlN
(iii) Reaction with H2 : At 200 atm and 773 K, and in the presence of iron catalyst and molybdenum promoter, N2 combines with H2 reversibly to form ammonia. The process is called Haber’s Process and is the industrial method of manufacturing ammonia. The reaction is exothermic.
N2 + 3H2 —® 2NH3
(iv)Reaction with oxygen: When air free from CO2 and moisture is passed over an electric arc at about 2000 K, nitric oxide is formed. This reaction is endothermic.
N2 + O2 —® 2NO
Uses :
1. For providing an inert atmosphere during many industrial processes where presence of air or O2 is to be avoided (e.g., in iron and steel industry, inert diluent for reactive chemicals).
2. For manufacture of NH3 by the Haber’s process.
3. For manufacture of HNO3 by the Birkeland-Eyde process.
4. For manufacture of industrial chemicals containing nitrogen like calcium cyanamide.
5. Liquid dinitrogen is used as a refrigerant to preserve biological materials, food items and in cryosurgery.
3. Ammonia
- Books Name
- ACME SMART COACHING Chemistry Book
- Publication
- ACME SMART PUBLICATION
- Course
- CBSE Class 12
- Subject
- Chemistry
Ammonia
Preparation :
(i) Ammonia is present in small quantities in air and soil where it is formed by the decay of nitrogenous orgainc matter e.g., urea.
NH2CONH2 + 2 H2O —® (NH4)2CO3 ![]() 2 NH3 + H2O + CO2
2 NH3 + H2O + CO2
(ii) On a small scale ammonia is obtaned from ammonia salts which decompose when treated with caustic soda or lime.
2 NH4Cl + Ca (OH)2 —® 2 NH3 + 2 H2O + CaCl2
(NH4)2 SO4 + 2 NaOH —® 2 NH3 + 2 H2O + Na2SO4
(iii) On a large scale, ammonia is manufactured by Haber’s process.
N2 (g) + 3 H2 (g) —® 2 NH3 (g) ; Df H– = – 46.1 kJ mol–1
In accordance with Le Chatelier’s principle, high pressure would favour the formation of ammonia. The optimum conditions for the production of ammonia are a pressure of 200 × 105 Pa (about 200 atm) , a temperature of ~ 700 K and the use of a catalyst such as iron oxide with small amounts of K2O and Al2O3 to increase the rate of attainment of equilibrium.
(iv) By hydrolysis of metal nitrides like AIN or Mg3N2
AIN + NaOH + H2O —® NaAIO2 + NH3
For drying, dehydrating agents like H2SO4 , P2O5 or CaCl2 can not be used as these react with NH3.
2NH3 + H2SO4 —® (NH4)2SO4 ; 6NH3 + P2O5 + 3H2O —® 2(NH4)3PO4
CaCl2 + 8NH3 —® CaCl2 8NH3 (Adduct)
So quicklime (CaO) is used for drying of NH3 .
CaO + H2O —® Ca(OH)2
Properties :
Physical properties : Ammonia is a colourless gas with a pungent odour. Its freezing and boiling points are 198.4 and 239.7 K respectively. In the solid and liquid states , it is associated through hydrogen bonds and that accounts for its higher melting and boiling points than expected on the basis of its molecular mass. The ammonia molecule is trigonal pyramidal with the nitrogen atom at the apex. It has three bond pairs and one lone pair of electrons as shown in the structure.
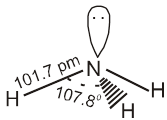
Ammonia gas is highly soluble in water. Its aqueous solution is weakly basic due to the formation of OH– ions. NH3 (g) + H2O (1) ![]() NH4+ (aq) + OH– (aq)
NH4+ (aq) + OH– (aq)
Chemical properties :
(i) It forms ammonium salts with acids , e.g., NH4Cl , (NH4)2 SO4 , etc. As a weak base , it precipitates the hydroxides of many metals from their salt solutions. For example ,
2 FeCl3 (aq) + 3 NH4OH (aq) —® Fe2O3 . xH2O (s) + 3 NH4Cl (aq)
(brown ppt)
(ii) The presence of lone pair of electrons on the nitrogen atoms of the ammonia molecule makes it a Lewis base. It donates the electrons pair and forms linkage with metal ions forming complex compounds.
Cu2+ (aq) + 4 NH3 (aq) ![]() [Cu(NH3)4]2+ (aq)
[Cu(NH3)4]2+ (aq)
(blue) (deep blue)
Ag+ (aq) + Cl–1 (aq) ![]() AgCl (s)
AgCl (s)
(colourless) (white ppt)
AgCl (s) + 2 NH3 (aq) —® [Ag (NH3)2]Cl (aq)
(white ppt) (colourless)
Test of ammonia/ammonium salts :
When NH3 gas is passed into the colourless solution of Nessler’s reagent a brown precipitate or coloration is formed. This is a test for NH3 gas.
2K2HgI4 + 3KOH + NH3 —® H2N·HgO·HgI ↓(brown) + 7KI + 2H2O
Uses :
1. Liquid ammonia is used as a refrigerant.
2. For the production of ammonium fertilizers such as ammonium sulphate, ammonium phosphate, ammonium nitrate, urea etc.
3. For removing grease because NH4OH dissolves grease.
4. For manufacture of HNO3 by the Ostwald process.
5. As a laboratory reagent.
6. In the production of artificial rayon, silk, nylon etc
4. Oxides of nitrogen
- Books Name
- ACME SMART COACHING Chemistry Book
- Publication
- ACME SMART PUBLICATION
- Course
- CBSE Class 12
- Subject
- Chemistry
Oxides of nitrogen
Nitrogen forms a number of oxides, N2O, NO, N2O3, NO2 or N2O4 and N2O5, and also very unstable NO3 and N2O6. All these oxides of nitrogen exhibit pπ-pπ multiple bonding between nitrogen and oxygen.
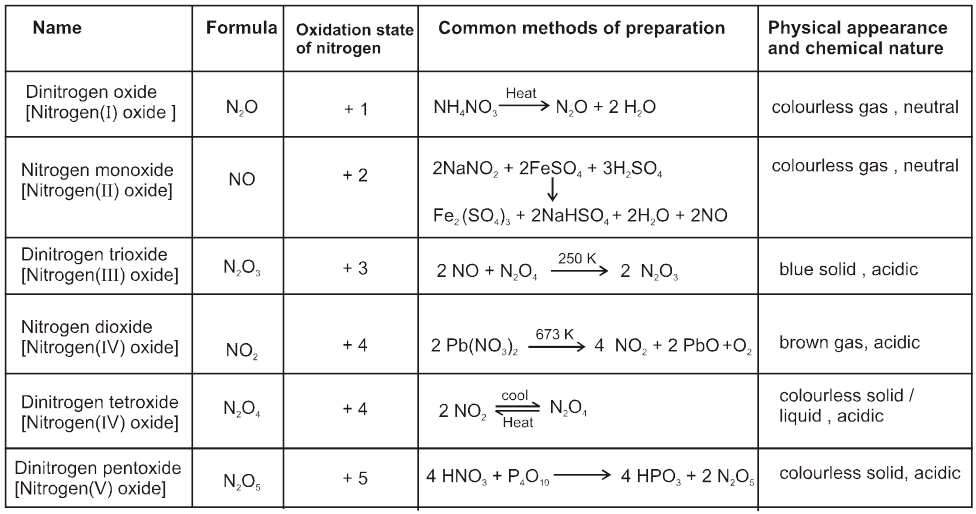
5. Nitric acid
- Books Name
- ACME SMART COACHING Chemistry Book
- Publication
- ACME SMART PUBLICATION
- Course
- CBSE Class 12
- Subject
- Chemistry
NITRIC ACID (HNO3)
Preparation :
(i) In the laboratory, nitric acid is prepared by heating KNO3 or NaNO3 and concentrated H2SO4 in a glass retort.
NaNO3 + H2SO4 —® NaHSO4 + HNO3
(ii) On a large scale it is prepared mainly by Ostwald’s process.
This method is based upon catalytic oxidation of NH3 by atmospheric oxygen.
4 NH3 (g) + 5 O2 (g) (from air) ![]() 4 NO (g) + 6 H2O (g)
4 NO (g) + 6 H2O (g)
Nitric oxide thus formed combines with oxygen giving NO2.
2 NO (g) + O2 (g) ![]() 2 NO2 (g)
2 NO2 (g)
Nitrogen dioxide so formed, dissolves in water to give HNO3.
3 NO2 (g) + H2O (l) —® 2 HNO3 (aq) + NO (g)
NO thus formed is recycled and the aqueous HNO3 can be concentrated by distillation upto ~ 68% by mass. Further concentration to 98% can be achieved by dehydration with concentrated H2SO4.
Properties :
Physical properties :
It is a colourless liquid. Freezing point is 231.4 K and boiling point is 355.6 K. Laboratory grade nitric acid contains ~ 68% of the HNO3 by mass and has a specific gravity of 1.504.
In the gaseous state, HNO3 exists as a planar molecule.
In aqueous solution, nitric acid behaves as a strong acid giving hydronium and nitrate ions.
HNO3 (aq) + H2O (l) —® H3O+ (aq) + NO3– (aq)
(i) Concentrated nitric acid is a strong oxidising agent and attacks most metals except noble metals such as gold and platinum. The products of oxidation depend upon the concentration of the acid , temperature and the nature of the material undergoing oxidation.
Some metals (e.g., Fe, Cr , Al) do not dissolve in concentrated nitric acid because of the formation of a passive film of oxide on the surface.
1. 4Zn + 10HNO3 (dilute) —® 4Zn(NO3)2 + N2O + 5H2O
Zn + 4HNO3 (concentrated) —® Zn(NO3)2 + 2NO2 + 2H2O
2. 3Cu + 8HNO3 (dilute) —® 2NO + Cu(NO3)2 + 4H2O
Cu + 4HNO3 (concentrated) —® 2NO2 + Cu(NO3)2 + 2H2O
(ii) Concentrated nitric acid also oxidises non–metals and their compounds. Iodine is oxidised to iodic acid , carbon to carbon dioxide , sulphur to H2SO4 and phosphorus to phosphoric acid.
I2 + 10 HNO3 —® 2 HIO3 + 10 NO2 + 4 H2O
C + 4 HNO3 —® CO2 + 2 H2O + 4 NO2
S8 + 48 HNO3 (concentrated) —® 8 H2SO4 + 48 NO2 + 16 H2O
P4 + 20 HNO3 (concentrated) —® 4 H3PO4 + 20 NO2 + 4 H2O
Brown Ring Test :
The familiar brown ring test for nitrates depends on the ability of Fe2+ to reduce nitrates to nitric oxide, which reacts with Fe2+ to form a brown coloured complex. The test is usually carried out by adding dilute ferrous sulphate solution to an aqueous solution containing nitrate ion , and then carefully adding concentrated sulphuric acid along the sides of the test tube. A brown ring at the interface between the solution and sulphuric acid layers indicate the presence of nitrate ion in solution.
NO3– + 3 Fe2+ + 4H+ —® NO + 3Fe3+ + 2 H2O
[Fe (H2O)6]2+ + NO —® [Fe (H2O)5 (NO)]2+ + H2O
Uses :
The major use of nitric acid is in the manufacture of ammonium nitrate for fertilizers and other nitrates for use in explosives and pyrotechnics. It is also used for the preparation of nitroglycerin, trinitrotoluene and other organic nitro compounds. Other major uses are in the pickling of stainless steel, etching of metals and as an oxidiser in rocket fuels.
6. Phosphorus - Allotropic forms
- Books Name
- ACME SMART COACHING Chemistry Book
- Publication
- ACME SMART PUBLICATION
- Course
- CBSE Class 12
- Subject
- Chemistry
PHOSPHORUS
It occurs in nature in the form of stable phosphates. (Animal bones also contain calcium phosphate (58 %)). The important minerals are:
(i) Phosphorite, Ca3(PO4)2
(ii) Chloraptite, Ca3(PO4)2CaCl2
(iii) Fluoraptite, Ca3(PO4)2CaF2
(iv) Vivianite, Fe3(PO4)2·8H2O (v) Redonda phosphate, AlPO4
Phosphorus Allotropic Forms :
Phosphorus is found in many allotropic forms , the important one being white , red and black.
White phosphorus :
Preparation :
2Ca3(PO4)2 (f`rom bone-ash) + 10C + 6SiO2 ![]() 6CaSiO3 + 10CO + P4(s) (electric furnace method)
6CaSiO3 + 10CO + P4(s) (electric furnace method)
It is a translucent white waxy solid. It is poisonous , insoluble in water but soluble in carbon disulphide. Molecular formula is P4. Ignition temperature is around 30ºC.
When exposed to air it undergoes oxidation which gradually raises it temperature and ultimately catches fire when the temperature exceeds 30ºC. That is why it is kept in water. White phosphorus is less stable and therefore , more reactive than the other solid phases under normal conditions because of angular strain in the P4 molecule where the angles are only 600.
It glows in dark due to slow oxidation. This property is called phosphorescence (chemiluminescence).
P4 + 5O2 ® P4O10
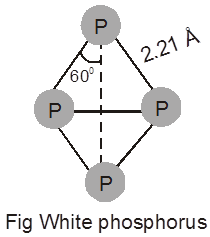
It consists of discrete tetrahedral P4 molecule as shown in Fig.
Red phosphorus is obtained by heating white phosphorus at 573 K in an inert atmosphere of CO2 or coal gas for several days. This red phosphorous may still contain some white phosphorus which is removed by boiling the mixture with NaOH when white phosphorus is converted in to PH3 gas but red phosphorus remains inert.
P4 + 3NaOH + 3H2O ® PH3(g) + 3NaH2PO2
When red phosphours is heated under high pressure, a series of phase of black phosphorus are formed. Red phosphorus possesses iron grey lustre. It is odourless , non – poisonous and insouble in water as well as in carbon disulphide. Chemically, red phosphorus is much less reactive than white phosphorus. It does not glow in the dark. Ignition temperature is 260ºC. It is polymeric, consisting of chains of P4 tetrahedra linked together in the manner as shown in Fig.
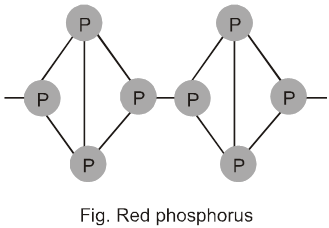
Black phosphorus has two forms a– black phosphorus and b – black phosphorus , a – Black phosphorus is formed when red phosphorus is heated in a sealed tube at 803 K. It can be sublimed in air and has opaque monoclinic or rhombohedral crystral. It does not oxidise in air.b – Black phosphorus is prepared by heating white phosphorus at 473 K under high pressure. It does not burn in air upto 673 K.
b - black phosphorus is a good conductor of electricity whereas a -Black phosphorus is non-conductor.
b - black phosphorus has layered structure like graphite. The distance between the two layers is found to be 3.68 Å.
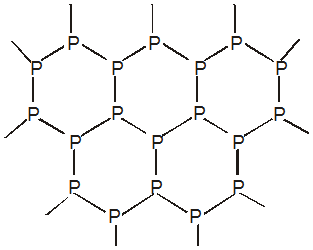
Density : White phosphorus= 1.83 ; Red phosphorus = 2.20 ; Black phosphorus = 2.70 gm/cc ;
As polymerisation increases compactness increases and therefore, density increases.
Reactivity of the various allotropic forms of phosphorus towards other substances decreases in the order:
white > red > black, the last one being almost inert i.e. most stable.
Apart from their reactivity difference, all the forms are chemically similar.
7. Compounds of Phosphorous
- Books Name
- ACME SMART COACHING Chemistry Book
- Publication
- ACME SMART PUBLICATION
- Course
- CBSE Class 12
- Subject
- Chemistry
COMPOUNDS OF PHOSPHORUS
Phosphine :
Preparation :
(i) Phosphine is prepared by the reaction of calcium phosphide with water or dilute HCl.
Ca3P2 + 6 H2O ® 3Ca(OH)2 + 2 PH3
Ca3P2 + 6HCl ® 3CaCl2 + 2PH3
(ii) In the laboratory, it is prepared by heating white phosphorus with concentrated NaOH solution in an inert atmosphere of CO2.
P4 + 3 NaOH + 3 H2O ® PH3 + 3 NaH2PO2
(sodium hypophosphite)
Pure PH3 is non inflammable but becomes inflammable owing to the presence of P2H4 or P4 vapours. For removal of impurify, it is absorbed in HI to form phosphonium iodide (PH4I) which on treating with KOH gives off phosphine.
PH4I + KOH ® KI + H2O + PH3
Properties :
(i) It is a colourless gas with a slightly garlic or rotten fish smell and is highly poisonous. It explodes in contact with traces of oxidising agents like HNO3, Cl2 and Br2 vapours.
(ii) It is slightly soluble in water but soluble in CS2 and other organic solvents. The solution of PH3 in water decomposes in presence of light giving red phosphorus and H2.
(iii)When absorbed in copper sulphate or mercuric chloride, the corresponding phosphides are obtained.
3CuSO4 + 2PH3 ® Cu3P2 ¯ (black) + 3H2SO4
3HgCl2 + 2 PH3 ® Hg3P2 ¯ (brownish black) + 6 HCl
(iv) Phosphine on heating at 150ºC burns forming H3PO4
PH3 + 2O2 ® H3PO4
(v) Phosphine is weakly basic and like ammonia, gives phosphonium compounds with acids e.g.,
PH3 + HBr ® PH4Br
Phosphonium compounds are obtained when anhydrous phosphine reacts with anhydrous halogen acids (not in aqueous solution).
Uses :
The spontaneous combustion of phosphine is made to use in Holme’s signals. Containers containing calcium carbide and calcium phosphide are pierced and thrown in the sea when the gases evolved burn and serve as a signal.
It is also used in the production of smoke screens. Calcium phosphide reacts with water producing phosphine which burns in air to give clouds of phosphorus pentaoxide and that acts as smoke screens.
8. Phosphorus halides
- Books Name
- ACME SMART COACHING Chemistry Book
- Publication
- ACME SMART PUBLICATION
- Course
- CBSE Class 12
- Subject
- Chemistry
Phosphorus Halides
Phsophorus forms two types of halides , PX3 [X = F , Cl , Br, I] and PX5 [X = F , Cl , Br]
(a) Phosphorus Trichloride :
Preparation :
(i) .It is obtained by passing dry chlorine over heated white phosphorus
P4 + 6 Cl2 ® 4 PCl3
(ii) It is also obtained by the action of thionyl chloride with white phosphorus.
P4 + 8 SOCl2 ® 4 PCl3 + 4 SO2 + 2 S2Cl2
Properties :
(i) It is a colourless oily liquid and hydrolyses in the presence of moisture.
PCl3 + 3 H2O ® H3PO3 + 3 HCl
(ii) It reacts with organic compounds containing – OH group such as CH3COOH , C2H5OH.
3 CH3COOH + PCl3 ® 3 CH3COCl + H3PO3
3 C2H5OH + PCl3 ® 3 C2H5Cl +H3PO3
(b) Phosphorus pentachloride :
Preparation :
Phosphorus pentachloride is prepared by the reaction of white phosphorus with excess of dry chlorine.
P4 + 10 Cl2 ® 4 PCl5
It can also be prepared by the action of SO2Cl2 on phosphorus.
P4 + 10 SO2Cl2 ® 4 PCl5 + 10 SO2
Properties :
(i) PCl5 is a yellowish white powder and in moist air , it hydrolyses to POCl3 and finally gets converted to phosphoric acid.
PCl5 + H2O ® POCl3 + 2 HCl
POCl3 + 3 H2O ® H3PO4 + 3 HCl
(ii) When heated it sublimes but decomposes on stronger heating.
PCl5  PCl3 + Cl2
PCl3 + Cl2
(iii) It reacts with organic compounds containing – OH group converting them to chloro derivatives.
C2H5OH + PCl5 ® C2H5Cl + POCl3 + HCl
CH3COOH + PCl5 ® CH3COCl + POCl3 + HCl
(iv) PCl5 on heating with finely divided metals give corresponding chlorides.
2 Ag + PCl5 ® 2 AgCl + PCl3
Sn + 2 PCl5 ® SnCl4 + 2 PCl3
It is used in the synthesis of some organic compounds , e.g., C2H5Cl , CH3COCl.
9. Oxoacids of phosphorus
- Books Name
- ACME SMART COACHING Chemistry Book
- Publication
- ACME SMART PUBLICATION
- Course
- CBSE Class 12
- Subject
- Chemistry
Oxides of phosphorus
(a) Phosphorus trioxide (P2O3) :
It is dimeric and has formula P4 O6
Preparation :
It is prepared by burning phosphorus in a limited supply of oxygen.
P4 + 3O2 (limited supply of oxygen) P4O6
Properties :
(i) It is colourless crystalline solid having melting point 23.8oC and boiling point 178oC.
(ii) It dissolves in cold water to form phosphorus acid and in hot water liberating PH3.
P4O6 + 6H2O (cold) ® 4H3PO3
P4O6 + 6H2O (hot) ® 3H3PO4 + PH3
(iii) It burns in Cl2 gas forming phosphorus oxytrichloride (POCl3) and phosphoryl chloride (PO2Cl)
P4O6 + 4Cl2 ® 2POCl3 + 2PO2Cl
(b) Phosphorus pentaoxide (P2O5) :
It is dimeric and has the formula P4O10.
Preparation :
It is obtained by burning phosphorus in excess air.
P4 + 5O2 ® P4O10
Properties:
(i) It is a white powder ,acidic in nature and is the anhydride of orthophosphoric acid.
(ii) It sublimes on heating at 250oC.
(iii) It dissolves in water with hissing sound forming metaphosphoric acid and finally orthophosphoric acid.
P4O10 + 2H2O ® 4HPO3
4HPO3 + 2H2O ® 2H4P2O7
2H4P2O7 + 2H2O ® 4H3PO4
(iv) It dehydrates concentrated H2SO4 and concentrated HNO3 to SO3 and N2O5 respectively.
4HNO3 + P4O10 ![]() 4HPO3 + 2N2O5
4HPO3 + 2N2O5
2H2SO4 + P4O10 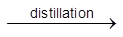 4HPO3 + 2SO3
4HPO3 + 2SO3
Uses:
1. For drying acidic gases.
2. As a dehydrating agent
3. For the preparation of SO3 and N2O5.
4. For the preparation of phosphoric acid.
Oxoacids of Phosphorus :
Phosphorus forms a number of a oxoacids as given in following Table :
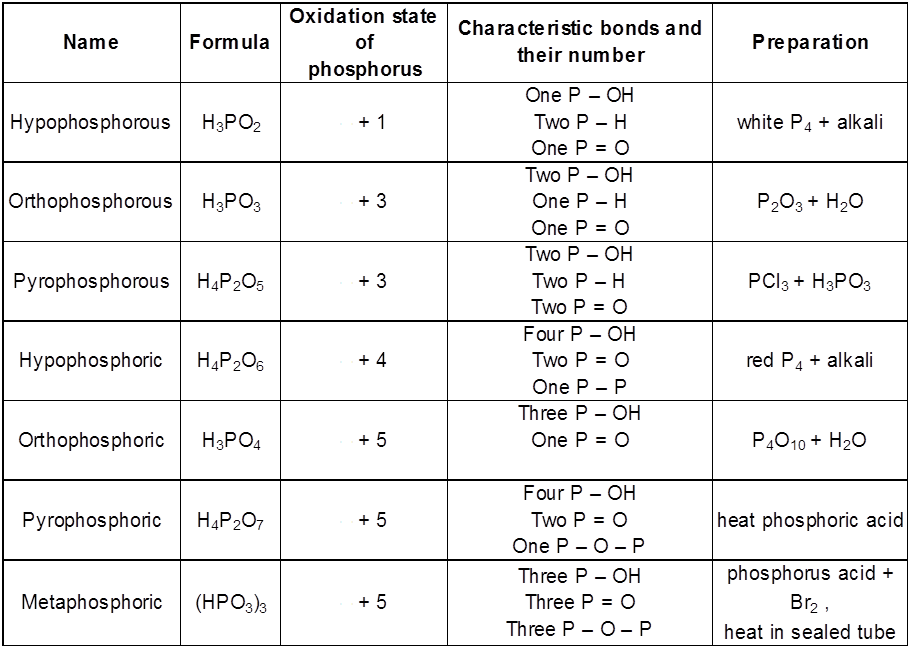
The structures of some of oxo-acids are as given below :
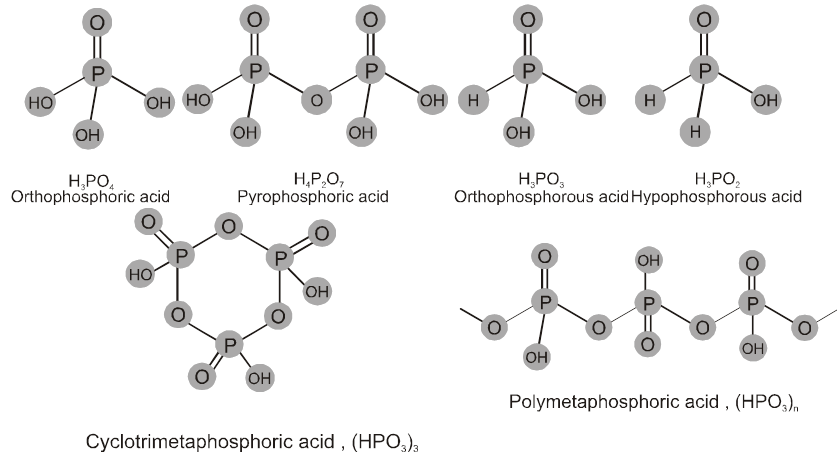
In oxoacids phosphorus is tetrahedrally surrounded by other atoms. All these acids contain one P=O and at least one P–OH bond. The oxoacids in which phosphorus has lower oxidation state (less than +5) contain in addition to P=O and P–OH bonds ,either P–P (e.g., in H4P2O6) or P–H (e.g., in H3PO2) bonds but not both. These acids in + 3 oxidation state of phosphorus tend to disproportionate to higher and lower oxidation states. For example, orthophosphorus acid (or phosphorus acid) on heating disproportionates to give orthophosphoric acid (or phosphoric acid) and phosphine.
4 H3PO3 ® 3 H3PO4 + PH3
The acids which contanin P – H bond have strong reducing properties. Thus , hypophorous acid is a good reducing agent as it contains two P – H bonds and reduces , for example, AgNO3 to metallic silver.
4 AgNO3 + 2 H2O + H3PO2 ®4 Ag + 4 HNO3 + H3PO4
These P–H bonds are not ionisable to give H+ and do not play any role in basicity. Only those H atoms which are attached with oxygen in P–OH form are ionisable and cause the basicity. Thus , H3PO3 and H3PO4 are dibasic and tribasic, respectively as the structure of H3PO3has two P – OH bonds and H3PO4 three.
10. Group 16 elements
- Books Name
- ACME SMART COACHING Chemistry Book
- Publication
- ACME SMART PUBLICATION
- Course
- CBSE Class 12
- Subject
- Chemistry
Group 16 Elements : The Oxygen family
Oxygen, sulphur, selenium, tellurium and polonium constitute group 16 of the periodic table. This is sometimes known as group of chalcogens the ore forming elements because a large number of metals ores are oxides or sulphides.
Electronic Configuration : The elements of group 16 have six electrons in the outermost shell and have ns2 np4 general valence shell electronic configuration.
Atomic and Ionic Radii : Due to increase in the number of shells , atomic and ionic radii increase from top to bottom in the group. The size of oxygen atoms is however, exceptionally small .
Ionisation Enthalpy : Ionisation enthalpy decreases down the group. It is due to increase in size. However, the element of this group have lower ionisation enthalpy values compared to those of group 15 in the corresponding periods. This is due to the fact that group 15 elements have extra stable half-filled p orbitals electronic configurations.
Electron Gain Enthalpy : Because of the compact nature of oxygen atom, it has less negative electron gain enthalpy than sulphur. However from sulphur onwards the value again becomes less negative upto polonium.
Electronegativity : Next to fluorine, oxygen has the highest electronegativity value amongst the elements. Within the group, electronegativity decrease with an increase in atomic number. This indicates that the metallic character increases from oxygen to polonium.
Physical Properties : Oxygen and sulphur are non-metal, selenium and tellurium metalloids, whereas polonium is a metal. Polonium is radioactive and is short lived (Half-life 13.8 days). The melting and boiling points increase with an increase in atomic number down the group. The larger difference between the melting and boiling points of oxygen and sulphur may be explained on the basis of their atomicity; oxygen exist as diatomic molecules (O2) whereas sulphur exists as polyatomic molecule (S8).
Catenation : Tendency for catenation decreases down the group. This property is prominently displayed by sulphur (S8). The S—S bond is important in biological system and is found in some proteins and enzymes such as cysteine.
Selenium has unique property of photo conductivity and is used in photocopying machines and also a decolouriser of glass.
Atomic & Physical Properties
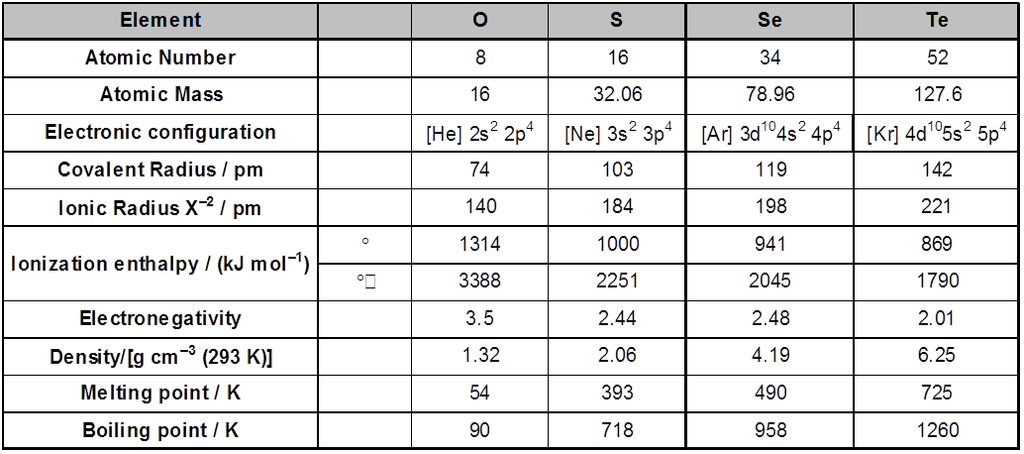
Chemical Properties :
Oxidation states and trends in chemical reactivity :
The elements of group 16 exhibit a number of oxidation states. The stability of -2 oxidation state decreases down the group. Polonium hardly shows -2 oxidation states. Since electronegativity of oxygen is very high, it shows only negative oxidation states as -2 except in the case of OF2 where its oxidation states is + 2. Other elements of the group exhibit + 2 + 4 + 6 oxidation states but + 4 and + 6 are more common. Sulphur, selenium and tellurium usually show + 4 oxidation in their compounds with oxygen and +6 oxidations state with fluorine. The stability of +6 oxidation state decreases down the group and stability of + 4 oxidation state increases (inert pair effect). Bonding in + 4 and + 6 oxidation states are primarily covalent.
HNO3 oxidises sulphur to H2SO4 (S + VI) but only oxidises selenium to H2SeO3 (Se + IV) as the atoms are smaller and there is poor shielding of 3d electrons as a result the electrons are held more tightly with nucleus.
Anomalous behaviour of oxygen :
The anomalous behaviour of oxygen, like other member of p-block present in second period is due to its small size and high electronegativity. One typical example of effects of small size and high electronegativity is the presence of strong hydrogen bonding in H2O which is not found in H2S.
The absence of d orbitals in oxygen restricts its covalency to four and in practice, rarely increases beyond two. On the other hand, in case of other elements of the group, the valence shell can be expanded and covalence exceeds four.
(i) Reactivity with hydrogen : All the elements of group 16 form hydrides of the type H2E (E = S, Se, Te, Po). Some properties of hydrides are given in Table. Their acidic character increases from H2O to H2Te. The increase in acidic character can be understood in terms of decrease in bond (H-E) dissociation enthalpy down the group. Owing to the decrease in bond (H-E) dissociation enthalpy down the group , the thermal stability of hydrides also decreases from H2O to H2Po. All the hydrides except water possess reducing property and this property increases from H2S to H2Te.
Table : Properties of Hydrides of Group 16 Elements
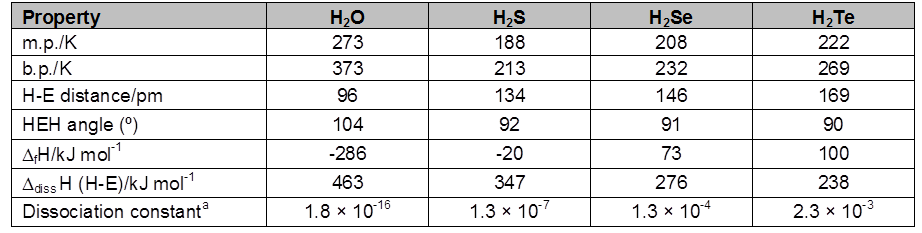
(ii) Reactivity with oxygen : All these elements form oxides of the EO2 and EO3 types where E = S, Se, Te or Po. Ozone (O3) and sulphur dioxide (SO2) are gases while selenium dioxide (SeO2) is solid. Reducing property of dioxide decreases from SO2 to TeO2 ; SO2 is reducing while TeO2 is an oxidising agent. Besides EO2 type sulphur, selenium and tellurium also form EO3 type oxides (SO3, SeO3, TeO3). Both types of oxides are acidic in nature.
(iii) Reactivity toward the halogens : Elements of group 16 form a larger number of halides of the type EX6, EX4 and EX2 where E is an element of the group and X is an halogen. The stabilities of the halides decrease in the order F > Cl > Br > l. Amongst hexahalides, hexafluorides are the only stable halides. All hexafluorides are gaseous in nature. They have octahedral structure. Sulphur hexafluoride SF6 is exceptionally stable for steric reasons.
Amongst tetrafluorides, SF4 is a gas , SeF4 liquid and TeF4 a solid.
All elements except selenium form dichlorides and dibromides.The well known monohalides are dimeric in nature, Examples are S2F2, S2Cl2, S2Br2, Se2Cl2 and Se2Br2. These dimeric halides undergo disproportionation as given below :
2Se2Cl2 ® SeCl4 + 3Se.
11. Dioxygen
- Books Name
- ACME SMART COACHING Chemistry Book
- Publication
- ACME SMART PUBLICATION
- Course
- CBSE Class 12
- Subject
- Chemistry
DIOXYGEN (O2)
It differs from the remaining elements of the VIth group because of the following properties.
(A) small size
(B) high electronegativity and
(C) non-availability of d-orbitals.
Preparation :
(i) By thermal decomposition of oxides of metals.
2 HgO ![]() 2 Hg + O2
2 Hg + O2
2 Ag2O ![]() 4 Ag + O2
4 Ag + O2
(ii) By thermal decomposition of oxygen rich compounds.
KClO3 ![]() 2 KCl + 3O2 (laboratory method)
2 KCl + 3O2 (laboratory method)
(iii) 2H2O2(aq.) ![]() 2H2O(l) + O2(g)
2H2O(l) + O2(g)
(iv) Industrial method :
(a) Electrolysis of water leads to the release of hydrogen at the cathode and oxygen at the anode.
(b) Oxygen is obtained by liquification of air and then its fractional distillation.
Physical properties :
Colourless , odourless and tasteless gas. It is paramagnetic and exhibits allotropy. Three isotopes of oxygen are ![]() ,
, ![]() and
and ![]() . Oxygen does not burn but is a strong supporter of combustion.
. Oxygen does not burn but is a strong supporter of combustion.
Chemical properties :
(i) Reaction with metals :
2Ca + O2 —® 2CaO
4Al + 3O2 —® 2Al2O3
(ii) Reaction with non-metals :
P4 + 5O2 —® P4O10
C + O2 —® CO2
(iii) Reaction with compounds :
2ZnS + 3O2 —® 2ZnO + 2SO2
CH4 + 2O2 —®CO2 + 2H2O
2SO2 + O2 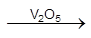 2SO3
2SO3
4HCl + O2 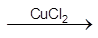 2Cl2 + 2H2O
2Cl2 + 2H2O
Note : It has been observed that its combination with other elements is often strongly exothermic which helps in sustaining the reaction. However, to initiate the reaction, some external heating is required as bond dissociation enthalpy of oxygen-oxygen double bond is high (493.4 kJ mol–1).
Use :
1. Oxygen mixed with helium or CO2 is used for artificial respiration.
2. Liquid oxygen (with combustion fuel hydrazine) is used as oxidising agent in rocket fuels.
3. Oxygen is used for production of oxy-hydrogen or oxy-acetylene flames employed for cutting and welding.
4. Pure dioxygen is used to convert pig iron into steel in the basic oxygen process which are kaldo and LD process.
12. Oxides
- Books Name
- ACME SMART COACHING Chemistry Book
- Publication
- ACME SMART PUBLICATION
- Course
- CBSE Class 12
- Subject
- Chemistry
OXIDES
(i) Acidic oxides :
The covalent oxides of non-metal are usually acidic; dissolves in water to produce solutions of acids e.g., CO2, SO2 , SO3, N2O5 , N2O3 , P4O6 , P4O10, Cl2O7, CrO3 , Mn2O7 etc. They are termed as acid anhydride.
Cl2O7 + H2O —® 2 HClO4
Mn2O7 + H2O —® 2 HMnO4
(ii) Basic oxides :
Metallic oxides are generally basic oxides. They either dissolve in water to form alkalies or combine with acids to form salts and water or combine with acidic oxides to form salts; e.g., Na2O, CaO. CuO, FeO, BaO etc.
Na2O + H2O —® 2 NaOH
CaO + H2O —® Ca(OH)2
CuO + H2SO4 —® CuSO4 + H2O
The metallic oxides with lowest oxidation sate is the most ionic and the most basic but with increasing oxidation sate the acidic character increases e.g., CrO is basic, Cr2O3 amphoteric and CrO3 acidic.
(iii) Amphoteric Oxides :
Many metals yield oxides which combine with both strong acid as well as strong bases e.g., ZnO, Al2O3, BeO, Sb2O3, Cr2O3, PbO, SnO, SnO2, Ga2O3 etc.
Cr2O3 + 2 NaOH —® Na2Cr2O4 + H2O
Cr2O3 + 3 H2SO4 —® Cr2(SO4)3 + 3 H2O
13. Ozone
- Books Name
- ACME SMART COACHING Chemistry Book
- Publication
- ACME SMART PUBLICATION
- Course
- CBSE Class 12
- Subject
- Chemistry
OZONE (O3)
O3 is an allotropic form of oxygen. At a height of about 20 Kms it is formed from atmoshperic oxygen in the presence of sunlight. This O3 layer protects the earth’s surface from an excessive concentration of ultra violet radiations.
Preparation :
It is prepared by passing silent electric discharge through a slow stream of pure and dry oxygen to prevent its decomposition.
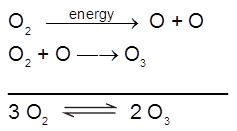
DHV (298 K) = + 142 kJ mol–1
The product is known as ozonised oxygen. If concentration of O3 greater than 10% are required , a battery of ozonisers can be used , and pure ozone (bp 385 K) can be condensed in a vessel surrounded by liquid oxygen.
Properties :
Physical properties :
(1) It is a pale blue gas which forms a blue liquid and one solidification forms violet black crystals.
(2) It has a strong fish – like smell
(3) It is slightly soluble in water but more in turpentine oil or glacial acetic acid or CCl4 .
(4) O3 molecule is diamagnetic but O3– ion is paramagnetic (1 unpaired e–)
(5) It is explosive and unstable with respect to O2 as its decomposition into O2 results in the liberation of heats and an increase in entropy.
Chemical Properties :
(1) As Oxidising agent : Due to the ease with which it liberates atoms of nascent oxygen
(O3 —® O2 + O ), it acts as a powerful oxidising agent.
In acidic medium :
O3 + 2 H+ + 2e– —® O2 + 2 H2O SRP = + 2.07 V.
In alkaline medium :
O3 + H2O + 2e– —® O2 + 2 OH– SRP = + 1..24 V
Therefore , Ozone is a stronger oxidising agent in acidic medium.
With excess of potassium iodide solution buffered with a borate buffer, ozone liberates iodine which can be titrated against a standard solution of sodium thiosulphate. This is a quantitative method for estimating O3 gas.
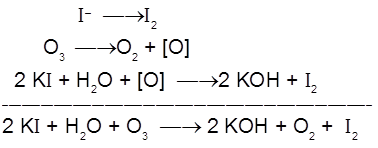
It oxidises PbS to PbSO4 , MnO42– to MnO4– (basic medium) and [Fe(CN)6]4– to [Fe(CN)6]3– (basic medium).
Note : With experimental facts it has been shown that nitrogen oxides (particularly nitric oxide) combine very rapidly with ozone and there is, thus, the possibility that nitrogen oxides emitted from the exhaust systems of supersonic jet aeroplanes might be slowly depleting the concentration of the ozone layer in the upper atmosphere.
NO(g) + O3 (g) —® NO2 (g) + O2 (g)

O–O bond length decreases in order : H2O2 (1.48 Å) > O3 (1.28 Å) > O2F2 (1.22 Å) > O2 (1.21 Å)
Uses :
It is used as a germicide, disinfectant and for sterilising water. It is also used for bleaching oil, ivory, flour starch etc. It acts as an oxidising agent in the manufacture of potassium permanganate
14. Sulphur - Allotropic forms
- Books Name
- ACME SMART COACHING Chemistry Book
- Publication
- ACME SMART PUBLICATION
- Course
- CBSE Class 12
- Subject
- Chemistry
SULPHUR (S)
Allotropic Forms Of Sulphur :
Sulphur forms numerous allotropes of which the yellow rhombic (a - sulphur) and monoclinic (b - sulphur) forms are the most important. The stable forms at room temperature is rhombic sulphur, which transforms to monoclinic sulphur when heated above 369 K.
Rhombic sulphur (a - sulphur) :
This allotrope is Syellow in colour , melting point 385.8 K and specific gravity 2.06. Rhombic sulphur crystals are formed on evaporating the solution of roll sulphur in CS2. It is insoluble in water but dissolved to some extent in benzene, alcohol and ether. It is readily soluble in CS2 .
Monoclinic sulphur (b - sulphur) :
Its melting point is 393 K and specific gravity 1.98. It is soluble in CS2. This form of sulphur is prepared by melting rhombic sulphur in a dish and cooling till crust is formed. Two holes are made in the crust and the remaining liquid poured out. On removing the crust, colourless needle shaped crystals of b - sulphur are formed. It is stable above 369 K and transforms into a - sulphur below it . Conversely,a - sulphur is stable below 369 K and transforms into b - sulphur above this. At 369 K both the forms are stable. This temperature is called transition temperature.
Both rhombic and monoclinic sulphur have S8 molecules these S8 molecules are packed to give different crystal structures. The S8 ring in both the forms is puckered and has a crown shape. The molecular dimensions are given in figure.
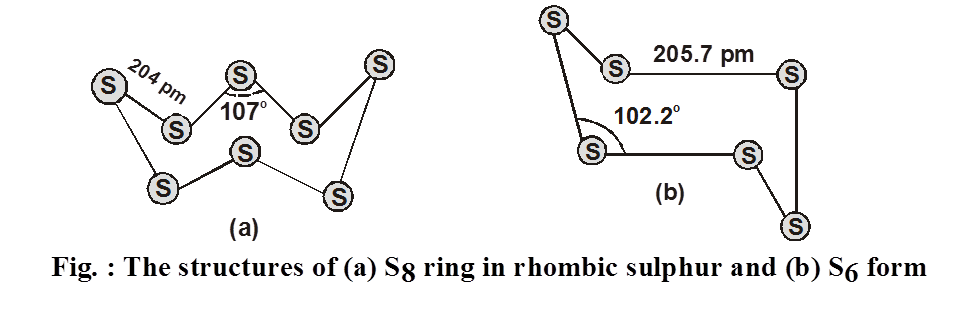
Several other modifications of sulphur containing 6-20 sulphur atoms per ring have been synthesised in the last two decades. In cyclo- S6, the ring adopts the chair form and the molecular dimension are as shown in fig. (b).
Sulphur melts to form a mobile liquid. As the temperature is raised the colour darkens. At 160ºC C8 rings break, and the diradicals so formed polymerize, forming long chains of up to a million atoms. The viscosity increases sharply, and continues to rise up to 200ºC. At higher temperatures chains break, and shorter chains and rings are formed, which makes the viscosity decrease upto 444ºC, the boiling point. The vapour at 200ºC consists mostly of S8 rings, but contains 1-2% of S2 molecules. At elevated temperature (~1000 K), S2 is the dominant species and is paramagnetic like O2, and presumably has similar bonding. S2 gas is stable upto 2200ºC.
15. Sulphur dioxide
- Books Name
- ACME SMART COACHING Chemistry Book
- Publication
- ACME SMART PUBLICATION
- Course
- CBSE Class 12
- Subject
- Chemistry
SULPHUR DIOXIDE
Perparation :
(i) Sulphur dioxide is formed together with a little (6-8%) sulphur trioxide when sulphur is burnt in air or oxygen:
S(s) + O2(g) ® SO2(g)
(ii) In the laboratory it is readily generated by treating a sulphite with dilute sulphuric acid.
SO32 – (aq) + 2H+ (aq) ® H2O(l) + SO2(g)
(iii) Industrially it is produced as a by- product of the roasting of sulphide ores.
4FeS2(s) + 11O2 (g) ®2Fe2O3(s) + 8SO2(g)
The gas after drying is liquefied under pressure and stored in steel cylinders.
Properties :
(i) Sulphur dioxide is a colorless gas with pungent smell and is highly soluble in water. It liquefies at room temperature under a pressure of two atomsphere and boils at 263 K.
(ii) Sulphur dioxide, when passed through water, forms a solution of sulphurous acid.
SO2(g) + H2O(l) ![]() H2 SO3 (aq)
H2 SO3 (aq)
(iii)It reacts readily with sodium hydroxide solution, forming sodium sulphite which then reacts with more sulphur dioxide to form sodium hydrogen sulphite.
2NaOH + SO2 — Na2SO3 + H2O
Na2SO3 + H2O + SO2 ® 2NaHSO3
(iv) In it reaction with water and alkalies, the behaivour of sulphur dioxide is very similar to that of carbon dioxide.
Sulphur dioxide reacts with chlorine in the presence of charcoal (which acts as a catalyst) to give sulphuryl chloride, SO2Cl2 It is oxidised to sulphur trioxide by oxygen in the presence of vanadium (v) oxide catalyst.
SO2(g) + Cl2(g) ® SO2Cl2(l)
2SO2 (g) + O2 (g) ![]() 2SO3(g) Addition reactions
2SO3(g) Addition reactions
(v) When moist, sulphur dioxide behaves as a reducing agent. For example it converts iron (III) ions to irons (II) ions and decolourises acidified potasssium permanganate (VII) solution; the latter reaction is a convenient test for the gas.
2Fe3+ + SO2 + 2H2O ® 2Fe2+ + SO42– + 4H+
5SO2 + 2MnO4– + 2H2O ® 5SO42– + 4H+ + 2Mn2+
(vi) Bleaching action :
SO2 + 2H2O ® H2SO4 + 2H
coloured matter ![]() colourless matter
colourless matter
Bleaching is through reduction but it is temporary.
It is a more powerful reducing agent in alkaline medium than in acidic medium.
Uses :
Sulphur dioxide is used (i) in refining petroleum and sugar (ii) in bleaching wool and silk and (iii) as an anti- chlor, disinfecatant and preservation. Sulphuric acid, sodium hydrogen sulphite and calcium hydrogen sulphite (industrial chemicals) are manufactured from sulphur dioxide. Liquid SO2 is used as a solvent to dissolve a number of organic and inorganic chemicals.
16. Oxoacids of sulphur
- Books Name
- ACME SMART COACHING Chemistry Book
- Publication
- ACME SMART PUBLICATION
- Course
- CBSE Class 12
- Subject
- Chemistry
OXYACID OF SULPHUR
Sulphur forms a number of oxoacid such as H2SO3, H2S2O4, H2S2O5, H2S2O6 (x = 2 to 5,) H2SO4, H2S2O7, H2SO8.Structures of some important oxoacids are shown in figure.
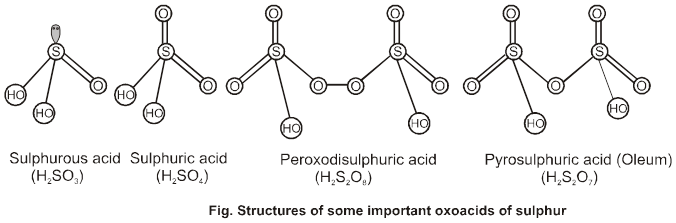
17. Sulphuric acid
- Books Name
- ACME SMART COACHING Chemistry Book
- Publication
- ACME SMART PUBLICATION
- Course
- CBSE Class 12
- Subject
- Chemistry
SULPHURIC ACID (H2SO4)
Manufacture :
Sulphuric acid is manufactured by the contact process which involves three steps :
(i) burning of sulphur or sulphide ores in air to generate SO2
(ii) conversion of SO2 to SO3 by the reaction with oxygen in the presence of a catalyst (V2O5), and
(iii) absorption of SO2 in H2SO4 to give Oleum (H2S2O7)
The SO2 produced is profiled by removing dust and other impurities such as arsenic compounds.
The key step in the manufacture of H2SO4 is the catalytic oxidation of SO2 with O2 to give SO3 in the presence of V2O5 (catalyst).
2SO2(g) + O2(g) ![]() 2SO3(g) DrH
2SO3(g) DrH![]() = – 196.6 kJ mol–1.
= – 196.6 kJ mol–1.
The reaction is exothermic reversible and the forward reaction leads to a decrease in volume. Therefore, low temperature and high pressure are the favourable conditions for maximum yield. But the temperature should not be very low other wise rate of reaction will become slow.
In practice the plant is operated at a pressure of 2 bar and a temperature of 720 K. The SO3 gas from the catalytic converter is absorbed in concentrated H2SO4 to produce oleum. Dilution of oleum with water gives H2SO4 of the desired concentration. In the industry two steps are carried out simultaneously to make the process a continuous one and also to reduce the cost.
SO3 + H2SO4 ® H2S2O7
(Oleum)
The sulphuric acid obtained by Contact process is 96-98% pure.
Properties :
Sulphuric acid is a colourless, dense, oily liquid with a specific gravity of 1.84 at 298 K. The acid freezes at 283 K and boils at 611 K. It dissolves in water with the evolution of a larger quantity of heat. The chemical reaction of sulphuric acid are as a result of the following characteristics : (a) low volatility (b) strong acidic character (c) strong affinity for water and (d) ability to act as an oxidising agent in aqueous solution,
(i) Sulphuric acid ionises in two steps.
H2SO4(aq) + H2O(l) ® H3O+ (aq) + HSO4– (aq)
Ka1 = very larger (Ka1 > 10)
H2SO4– (aq) + H2O(l) ® H3O+ (aq) + SO42– (aq)
Ka2 = 1.2 × 10–2
The larger value of Ka1 (Ka1 > 10) means that H2SO4 is largely dissociated into H+ and HSO4–. Greater the value of dissociation constant (Ka) the stronger is the acid.
(a) The acid forms two series of salts : normal sulphates (such as sodium sulphate and copper sulphate and acid sulphate (e.g., sodium hydrogen sulphate)
(b) Decomposes carbonates and bicarbonates in to C.
Na2CO3 + H2SO4 ® Na2SO4 + H2O + CO2
NaHCO3 + H2SO4 ® NaHSO4 + H2O + CO2
(c) Sulphuric acid, because of its low volatility can be used to manufacture more volatile acid from their corresponding salts.
2MX + H2SO4 ® 2HX + M2SO4 (X = F, Cl, NO3
NaCl + H2SO4 ® NaHSO4 + HCl
(M = Metal)
(ii) Concentrated sulphuric acid is a strong dehydrating agent. Many wet gases can be dried by passing them through sulphuric acid, provided the gases do not react with the acid. Sulphuric acid removes water from organic compound; it is evident by its charring action on carbohydrates.
C12H22O11 ![]() 12C + 11H2O
12C + 11H2O
H2C2O4![]() CO + CO2
CO + CO2
(iii) Hot concentrated sulphuric acid is moderately strong oxidising agent. In this respect it is intermediate between phosphoric and nitric acids. Both metals and non-metals are oxidised by concentrated sulphuric acid, which is reduced to SO2.
Cu + 2H2SO4 (concentrated) ® CuSO4 + 2H2O
3S + 2H2SO4 (concentrated) ® 3SO2 + 2H2O
C + 2H2SO4 (concentrated) ® CO2 + 2SO2 + 2H2O
Uses :
Sulphuric acid is a very important industrial chemical. A nation’s industrial strength can be judged by the quantity of sulphuric acid it produces and consumes .It is needed for the manufacture of hundreds of other compounds also in many industrial processes .The bulk of sulphuric acid produced is used in the manufacture of fertilisers (e.g., ammonium sulphate, superphosphate). Other uses are in : (i) petroleum refining (ii) manufacture of pigment, paints and dyestuff intermediates (iii) detergent industry (iv) metallurgical applications (e.g., cleansing metal before enameling, electroplating and galvanising) (v) storage batteries (vi) in the manufacture of nitrocellulose products and (vii) as a laboratory reagent.
2. Chlorine
- Books Name
- ACME SMART COACHING Chemistry Book
- Publication
- ACME SMART PUBLICATION
- Course
- CBSE Class 12
- Subject
- Chemistry
CHLORINE (Cl2)
Preparation :
(i) By heating MnO2 with concentrated hydrocloric acid.
MnO2 + 4HCl ® MnCl2 + Cl2 + 2H2O
(ii) By heating chloride with concentrated H2SO4 in presence of MnO2.
4H+ + MnO2 + 2X– ® X2 + Mn+2 + 2H2O
(iii) 2KMnO4 + 16 HCl ® 2 KCl + 2 MnCl2 + 5 Cl2 + 8 H2O
(iv) Manufacture of chlorine :
(a) Deacon’s process : By oxidation of hydrogen chloride gas by atmospheric oxygen in the presence of CuCl2 (catalyst) at 723 K.
4 HCl + O2 ![]() 2 Cl2 + 2 H2O
2 Cl2 + 2 H2O
(b) Electrolytic process : Chlorine is obtained by the electrolysis of brine (concentrated NaCl solution). Chlorine is liberated at anode. It is obtained as a by–product in many chemical industries e.g.; in mfg. of sodium hydroxide.
NaX (aq) ® Na+ (aq) + X– (aq)
Anode : 2X– ® X2 + 2e–
Properties :
(i) It is a greenish–yellow gas with pungent and suffocating odour. It is about 2–5 times heavier than air. It can be liquefied into greenish–yellow liquid which boils at 239 K. It is soluble in water.
(ii) At low temperature it forms a hydrate with water having formula Cl2 . 8H2O which is infact a clathrate compound.
(iii) Reaction with metals :
2Al + 3Cl2 ® 2AlCl3
2Fe + 3Cl2 ® 2FeCl3
Reaction with non-metals :
P4 + 6Cl2 ® 4PCl3
S8 + 4Cl2 ® 4S2Cl2
(iv) Affinity for hydrogen : It reacts with compounds containing hydrogen and form HCl.
H2 + Cl2 ® 2HCl
H2S + Cl2 ® 2HCl + S
(v) Reaction with NaOH :
(a) 2 NaOH ( cold & dilute) + Cl2 ® NaCl + NaClO + H2O
(b) 6 NaOH (hot & concentrated) + 3 Cl2 ® 5 NaCl + NaClO3 + 3 H2O
(vi) Reaction with dry slaked lime, Ca(OH)2 : To give bleaching powder.
2 Ca(OH)2 + 2 Cl2 ® Ca(OCl)2 + CaCl2 + 2 H2O
The composition of bleaching powder is Ca(OCl)2.CaCl2.Ca(OH)2 .2H2O
(vii) Oxidising & bleaching properties :
Chlorine dissolves in water (Cl2 water is yellow) giving HCl (colourless) and HOCl (colourless). Hypochlorous acid (HOCl) so formed, gives nascent oxygen which is responsible for oxidising and bleaching properties of chlorine.
(a) It oxidises ferrous to ferric, sulphite to sulphate, sulphur dioxide to sulphuric acid and iodine to iodic acid.
2 FeSO4 + H2SO4 + Cl2 ® Fe2(SO4)3 + 2 HCl
Na2SO3 + Cl2 + H2O ® Na2SO4 + 2 HCl
SO2 + 2 H2O + Cl2 ® H2SO4 + 2 HCl
I2 + 6 H2O + 5 Cl2 ® 2 HIO3 + 10 HCl
(b) It is a powerful bleaching agent ; bleaching action is due to oxidation.
Cl2 + H2O ® 2 HCl + O
Coloured substance + O ® Colourless substance
It bleaches vegetable or organic matter in the presence of moisture. Bleaching effect of chlorine is permanent.
Note :
The bleaching action of SO2 is temporary because it takes place through reduction.
SO2 + 2 H2O ® H2 SO4 + 2 H
SO32– + Coloured material SO42– + Reduced colourless material.
Reduced Colourless material ![]() Coloured material.
Coloured material.
Uses : Cl2 is used
1. for bleaching wood pulp (required for the manufacture of paper and rayon), bleaching cotton and textiles,
2. in the manufacture of dyes, drugs and organic compounds such as CCl4, CHCl3, DDT, refrigerants, etc.
3. in the extraction of gold and platinum.
4. in sterilising drinking water and
5. preparation of poisonous gases such as phosgene (COCl2), tear gas (CCl3NO2), mustard gas (ClCH2CH2SCH2CH2Cl).
3. Hydrogen chloride
- Books Name
- ACME SMART COACHING Chemistry Book
- Publication
- ACME SMART PUBLICATION
- Course
- CBSE Class 12
- Subject
- Chemistry
HYDROGEN CHLORIDE (HCl)
Preparation :
By heating a halide with concentrated acid (Laboratory method) :
NaCl + H2SO4![]() NaHSO4 + HCl
NaHSO4 + HCl
NaHSO4 + NaCl ![]() Na2SO4 + HCl
Na2SO4 + HCl
This method is called as salt cake method as it involves the formation of NaHSO4 (salt cake).
HCl cannot be dried over P2O5 (P4O10) or quick lime since they react with gas chemically.
CaO + 2HCl ® CaCl2 + H2O
P4O10 + 3HCl ® POCl3 + 3HPO3
HCl is, hence dried by passing through concentrated H2SO4 .
Properties :
(i) It is a colourless, pungent smelling gases with acidic tastes.
(ii) It is easily liqueflied to a colourless liquid (b.p. 189 K) and freezes to a white crystalline solid (f.p. 159 K).
(iii) It is quite soluble in water.
HCl ionises as below : HCl(g) + H2O (l) ® H3O+ (aq) + Cl– (aq) ; Ka = 107
It aqueous solution is called hydrochloric acid. High value of dissociation constant (Ka) indicates that it is a strong acid in water.
When three parts of concentrated HCl and one part of concentrated HNO3 are mixed, aqua regia is formed which is used for dissolving noble metals, e.g., gold, platinum.
Au + 4 H+ + NO3– + 4 Cl– ® [AuCl4]– + NO + 2 H2O
3 Pt + 16 H+ + 4 NO3– + 18 Cl– 3 [PtCl6]2– + 4 NO + 8 H2O
It reacts with ammonia forming white fumes of NH4Cl
NH3 + HCl ® NH4Cl
(iv) It decomposes salt of weaker acids.
Na2CO3 + 2HCl ® 2NaCl + H2O + CO2
NaHCO3 + HCl ® NaCl + H2O + CO2
Na2SO3 + 2HCl ® 2NaCl + H2O+ SO2
Uses :
1. HCl is used in preparation of Cl2, chlorides, aqua regia, glucose, (from corn starch),
2. It is used in medicines, laboratory as reagents, cleaning metal surfaces before soldering or electroplating.
3. It is used for extracting glue from bones and purifying bone black.
4. Oxoacids of halogens
- Books Name
- ACME SMART COACHING Chemistry Book
- Publication
- ACME SMART PUBLICATION
- Course
- CBSE Class 12
- Subject
- Chemistry
OXY-ACIDS OF Halogens
Fluorine forms only one oxoacid, HOF due to high electronegativity and small size. Other halogens form a number of oxoacids which are stable only in aqueous solutions or in the form of their salts. They can not be isolated in pure form.
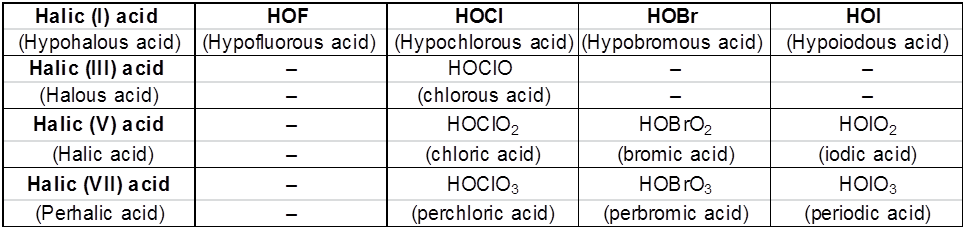
Some important order
(a) Acid strength
(i) HI > HBr > HCl > HF
(ii) HOCl > HOBr > HOI
(iii) HClO4 > HClO3 >HClO2 > HClO
(b) Oxidising powder
(i) F2 > Cl2 > Br2 > I2
(ii) BrO4– > IO4– > ClO4– (According to electrode potential)
(c) Order of disproportionations
3 XO– ® 2X– + XO3– (hypohalite ion) ;
IO– > BrO– > ClO–
5. Interhalogen compounds
- Books Name
- ACME SMART COACHING Chemistry Book
- Publication
- ACME SMART PUBLICATION
- Course
- CBSE Class 12
- Subject
- Chemistry
Interhalogen compounds
We know that halogen atoms have different electronegativity. Due to this difference in electronegativity the halogen atoms combine with each other and give rise to the formation of binary covalent compounds, which are called interhalogen compounds. These are of four types.
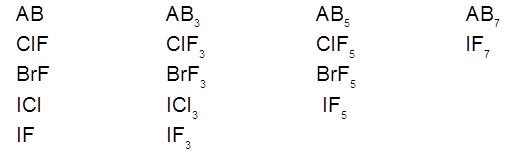
Preparation :
Cl2 + F2 (equal volumes) ![]() 2ClF
2ClF
Cl2 + 3F2 (excess) ![]() 2ClF3
2ClF3
I2 + Cl2 ® 2ICl ;
(equimolar)
Diluted with water :
Br2 (g) + 3F2 ® 2BrF3
F2 is diluted with N2 :
I2 + 3F2 ![]() 2IF3
2IF3
F2 is taken in freon :
Br2 + 5F2 (excess) ® 2BrF5
Properties :
(i) These compounds may be gases, liquids or solids.
Gases : ClF, BrF, ClF3 , IF7
Liquids : BrF3, BrF5
Solids : ICl, IBr, IF3, ICl3.
(ii) All interhalogens are covalent molecules and are diamagnetic in nature since all the valence electrons present as bonding or non-bonding electrons are paired.
(iii) The boiling points increases with the increase in the electronegativity difference between A and B atoms.
(iv) Interhalogen compounds are more reactive than the parent halogens but less reactive than F2.
(v) Hydrolysis : All these undergo hydrolysis giving halide ion derived from the smaller halogen and a hypohalite (when AB), halite (when AB3), halate (when AB5), and perhalate (when AB7) anion derived from the larger halogen.
AB + H2O ® HB + HOA
BrCl + H2O ® HCl + HOBr
ICl + H2O ® HCl + HIO2
Uses :
(i) These compounds can be used as non aqueous solvents.
(ii) Interhalogen compounds are very useful fluorinating agents.
(iii) ClF3 and BrF3 are used for the production of UF6 in the enrichment of 235U.
U(s) + 3 ClF3 (l) ® UF6 (g) + 3 ClF (g)
6. Group 18 elements
- Books Name
- ACME SMART COACHING Chemistry Book
- Publication
- ACME SMART PUBLICATION
- Course
- CBSE Class 12
- Subject
- Chemistry
Group 18 Elements : The Zero Group Family
Group 18 consists of six elements: helium, neon, argon, krypton , xenon and radon . All these are gases and chemically unreactive. They form very few compounds . Because of this they are termed noble gases.
Occurrence : All the noble gases except radon occur in the atmosphere. Their atmospheric abundance in dry air is ~ 1% by volume of which argon is the major constituent. Helium and sometimes neon are found in minerals of radioactive origin e.g., pitchblende, monazite, cleveite. The main commercial source of helium is natural gas. Xenon and radon are the rarest elements of the group. Radon is obtained as a decay product of 226Ra.
![]()
Most abundant element in air is Ar. Order of abundance in the air is Ar > Ne > Kr > He > Xe.
Electronic Configuration : All noble gases have general electronic configuration ns2np6 except helium which has 1s2 . Many of the properties of noble gases including their inactive nature are ascribed to their closed shell structures.
Ionisation Enthalpy : Due to stable electronic configuration these gases exhibit very high ionisation enthalpy . However, it decreases down the group with increases in atomic size.
Atomic Radii : Atomic radii increase down the group with increase in atomic number.
Electron Gain Enthalpy : Since noble gases have stable electronic configurations, they have no tendency to accept the electron and therefore, have larger positive values of electron gain enthalpy.
Physical properties : All the noble gases are mono-atomic. They are colourless, and tasteless. They are sparingly soluble in water. They have very low melting and boiling points because the only type of interatomic interaction in these elements is weak dispersion forces,. Helium has the lowest boiling point (4.2K) of any known substance. It has a unusual property of diffusing through most commonly used laboratory materials such as rubber, glass or plastics.
Atomic & physical properties
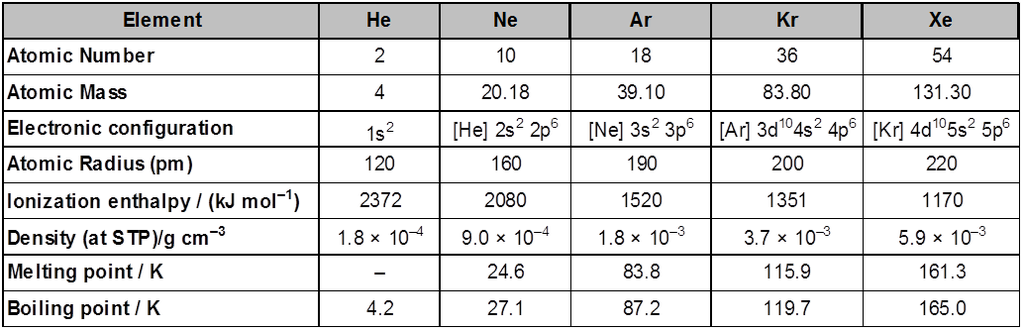
Chemical Properties :
In general, noble gases are least reactive. Their inertness to chemical reactivity is attributed to the following reasons :
(i) The noble gases except helium (1s2) have completely filled ns2 np6 electronic configuration in their valence shell.
(ii) They have high ionisation enthalpy and more positive electron gain enthalpy.
The reactivity of noble gases has been investigated occasionally ever since their discovery, but all attempt to force them to react to form the compounds were unsuccessful for quite a few years. In March 1962, Neil Bartlett, then at the University of British Columbia, observed the reaction of a noble gas. First , he prepared a red compound which is formulated as O2+ PtF6–. He , then realised that the first ionisation enthalpy of molecular oxygen (1175 kJ mol –1) was almost identical with that xenon (1170 kJ mol–1). He made efforts to prepare same type of compound with Xe+ PtF6– by mixing Pt F6 and Xenon. After this discovery, a number of xenon compounds mainly with most electronegative elements like fluorine and oxygen, have been synthesised.
The compounds of krypton are fewer. Only the difluoride (KrF2) has been studied in detail. Compounds of radon have not been isolated but only identified (e.g., RnF2) by radiotracer technique. No true compounds of Ar, Ne or He are yet known .
7. Compounds of Xenon
- Books Name
- ACME SMART COACHING Chemistry Book
- Publication
- ACME SMART PUBLICATION
- Course
- CBSE Class 12
- Subject
- Chemistry
COMPOUNDS OF XENON
Xenon–FLUORINE compounds :
All fluorides of xenon are white solids. They are volatile, readily subliming at room temperature (298 K)
![]()
They can be stored indefinitely in nickel or monel metal containers.
Xenon difluoride
Xe + F2 (2 : 1 mixture) ![]() XeF2 .
XeF2 .
It is soluble in water, giving solution 0.15 M at 0ºC. The solution which have pungent smell due to XeF2 are powerful oxidizing agents.
XeF2(aq) + 2H+ + 2e– ® Xe + 2HF(aq) ; Eº = + 2.64 V
XeF2 + H2 ®2 HF + Xe
Hydrolysis is slow in water due to dissolution of XeF2 in HF formed, but is rapid in basic solution.
2Xe F2 + 2H2O ®2 Xe + 4HF + O2
XeF2 + 2OH– ® Xe + ![]() O2 + 2F– + H2O
O2 + 2F– + H2O
It acts as fluoride ion donor XeF2 (Lewis base) + PF5 (Lewis acid) [XeF]+ [PF6]–
Xenon tetrafluoride
Xe + 2F2 (1 : 5 mixture)  XeF4
XeF4
XeF4 reacts violently with water, giving dangerously explosive XeO3.
6XeF4 + 12H2O ® 4Xe + 2 XeO3 + 24 HF + 3O2
XeF4 can act as F– acceptor as well as F– donors and thus form anionic species in reactions such as :
XeF4 + NaF ® Na+ XeF5–
XeF4 + SbF5 ® [XeF3]+ [SbF6]–
Xenon hexafluoride
Xe + 3F2 (1 : 20 mixture) ![]() XeF6
XeF6
XeF4 + O2 F2 ® XeF6 + O2
XeF6 reacts violently with water but slow hydrolysis with atmospheric moisture giving XeO3.
XeF6 + 6 H2O ® XeO3 + 6HF (complete hydrolysis)
With small quantities of water, partial hydrolysis takes place.
XeF6 + H2O ® XeOF4 (colourless liquid) + 2HF
XeF6 + 2 H2O ® XeO2F2 + 4HF
XeF6 reacts with fluoride ion donors to form fluoroanions.
XeF6 + MF® M+ [XeF7]– (M = Na, K, Rb or Cs)
Xenon–oxygen compounds :
Hydrolysis of XeF4 and XeF6 with water gives XeO3.
6 XeF4 + 12 H2O ® 4 Xe + 2 XeO3 + 24 HF + 3 O2
XeF6 + 3 H2O ® XeO3 + 6 HF
Partial hydrolysis of XeF6 gives oxyfluorides, XeOF4 and XeO2F2 .
XeF6 + H2O ®XeOF4 + 2 HF
XeF6 + 2 H2O ® XeO2F2 + 4 HF
XeO3 is a colourless explosive solid and has a pyramidal molecular structure. XeOF4 is a colourless volatile liquid and has a square pyramidal molecular structure.
Uses :
Helium is a non–inflammable and light gas. Hence, it is used in filling balloons for meteorological observations. It is also used in gas–cooled nuclear reactors. Liquid helium (b.p.4.2 K) finds use as cryogenic agent for carrying out various experiments at low temperatures. It is used to produce and sustain powerful superconducting magnets which form an essential part of modern NMR spectrometers and Magnetic Resonance Imaging (MRI) systems for clinical diagnosis. It is used as a diluent for oxygen in modern diving apparatus because of its very low solubility in blood.
Neon is used in discharge tubes and fluorescent bulbs for advertisement display purposes. Neon bulbs are used in botanical gardens and in green houses.
Argon is used mainly to provide an inert atmosphere in high temperature metallurgical processes (arc welding of metals or alloys) and for filling electric bulbs. It is also used in the laboratory for handlsing substances that are air–sensitive.
Xenon and Krypton are used in light bulbs designed for special purposes
2. Silver nitrate
- Books Name
- ACME SMART COACHING Chemistry Book
- Publication
- ACME SMART PUBLICATION
- Course
- CBSE Class 12
- Subject
- Chemistry
Silver nitrate
Silver nitrate, AgNO3 (Lunar Caustic)
Physical Properties
(i) It is a colourless crystalline compound.
(ii) Soluble in water and alcohol.
(iii) It melts at 212°C.
Chemical Properties
(i) It possesses powerful corrosive action on organic tissues, which at turns black especially in presence of light. The blackening is due to finely divided metalic silver, reduced by organic tissure It is therefore, stored in colored Bottles.
(ii) Solutions of halides phosphates, sulfides chromates thiocyanates, sulphates and thiosulphates salt with silver nitrate solution.
(iii) Ammonical silver nitrate is called as Tollen's reagent and used to identify reducing sugars and aldehydes.
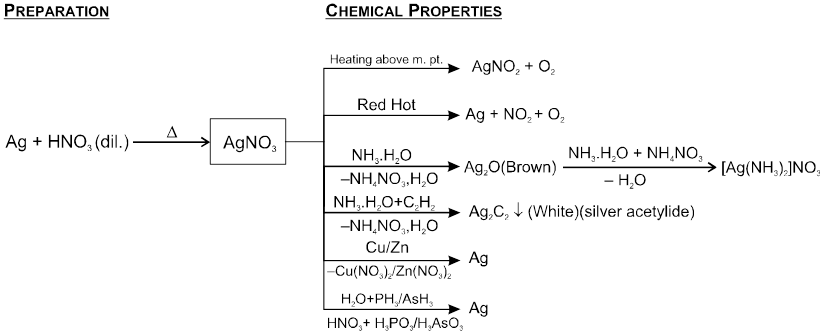
It is known as silver mirror test of aldehydes and reducing sugars.
Ag2O + HCHO ¾¾® 2Ag + HCOOH.
Ag2O + C6H12O6 ¾¾® 2Ag + C6H12O7.
(iv) Reactions with Iodine :
6 AgNO3 (excess) + 3I2 +3H2O ¾¾® AgIO3 + 5AgI + 6HNO3
5 AgNO3 + 3I2 (excess) +3H2O ¾¾® HIO3 + 5AgI + 5HNO3
Uses : It is used
- as a laboratory reagent for the identification of various acidic especially for Cl, Br and I
- Tollen's reagent is used in organic chemistry for testing aldehydes reducing sugars etc.
- for making AgBr, used in photography.
- in the preparation of inks and hair dyes.
- in preparation of silver mirror.
2. Photography :
(i) A photographic film consists of a light sensitive emulsion of fine particles (grains) of silver salts in gelatine spread on a clear celluloid strip or a glass plate. AgBr is mainly used as the light sensitive material.
(ii) The film is placed in a camera. When the photograph is exposed, light from the subject enters the camera and is focussed by the lens to give a sharp image on the film. The light starts a photochemical reaction by exciting a halide ion, which loses an electron. The electron moves in a conduction band to the surface of the grain, where it reduces a Ag+ ion to metallic silver.
2AgBr(s) ![]() 2Ag + Br2
2Ag + Br2
(iii) In modern photography only a short exposure of perhaps 1/100th of a second is used. In this short time, only a few atoms of silver (perhaps 10–50) are produced in each grain exposed to light. Parts of the film which have been exposed to the bright parts of the subject contain a lot of grains with some silver.
(iv) Next the film is placed a developer solution. This is a mild reducing agent, usually containing quinol. Its purpose is to reduce more silver halide to Ag metal. Ag is deposited mainly where there are already some Ag atoms. Thus the developing process intensifies the latent image on the film so it becomes visible.
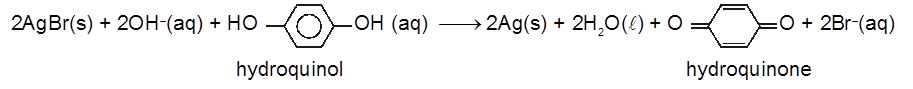
(v) If the film was brought out into daylight at this stage, the unexposed parts of the emulsion would turn black and thus destroy the picture. To prevent this happening any unchanged silver halides are removed by placing the film in a fixer solution. A solution of sodium thiosulphate is used as fixer. It forms a soluble complex with silver halides.
AgBr + 2Na2S2O3 ® Na3[Ag(S2O3)2] + NaBr
After fixing, the film can safely be brought out into daylight. This is called "negative".
Light is passed through the negative onto a piece of paper coated with AgBr emulsion. This is then developed and fixed in the same way as before.
3.Potassium Permanganatic (KMnO4)
- Books Name
- ACME SMART COACHING Chemistry Book
- Publication
- ACME SMART PUBLICATION
- Course
- CBSE Class 12
- Subject
- Chemistry
Potassium Permanganatic (KMnO4)
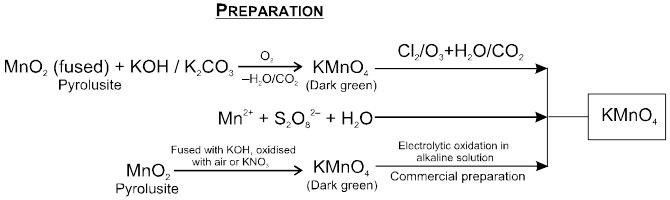
Physical Properties:
Purple coloured crystalline compound.
Moderately soluble in water at room temperature.
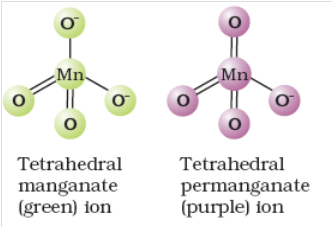
Structure of manganate and permanganate ion.
Chemical Properties
(i) Heating effect
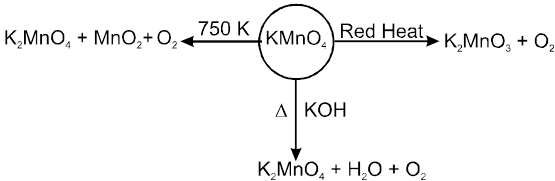
MnO42– in dilute alkaline, water and acidic solutions is unstable and disproportionates to give MnO4– and MnO2.
3MnO42– + 4H+ ¾®2MnO4– + MnO2 ¯ + 2H2O
3MnO42– + 2H2O ¾® 2MnO4– + MnO2 ¯ + 4OH–
or
3MnO42– + 3H2O ¾® 2MnO4– + MnO (OH)2 ¯+ 4OH–
On heating in current of H2 , solid KMnO4 gives MnO
2KMnO4 + 5H2 ![]() 2KOH + 2MnO + 4H2O
2KOH + 2MnO + 4H2O
(ii) On treatment with concentrated H2SO4 (KMnO4 is taken in excess), it forms manganese heptoxide via permanganyl sulphate which decomposes explosively on heating.
2KMnO4 + 3H2SO4 ¾® 2KHSO4 + (MnO3)2SO4 + 2H2O
(MnO3)2SO4 + H2O ¾® Mn2O7 + H2SO4
Mn2O7 ¾® 2MnO2 + ![]() O2
O2
KMnO4 + 3H2SO4 (conc.) ¾® K+ + MnO3+ (green) + 3HSO4– + H3O+.
(iii) Potassium permanganate is a powerful oxidising agent.
Potassium permanganate acts as an oxidising agent in alkaline, neutral or acidic solutions.
A mixture of sulphur, charcoal and KMnO4 forms an explosive powder. A mixture of oxalic acid and KMnO4 catches fire spontaneous after a few seconds. The same thing happens when glycerine is poured over powdered KMnO4.
In alkaline & neutral medium :
In strongly alkaline medium KMnO4 is reduced to manganate.
2KMnO4 + 2KOH (conc.) ¾® 2K2 MnO4 + H2O + [O]
or e– + MnO4– ¾® MnO42–
if solution is dilute then K2MnO4 is converted in to MnO2 which appears as a brownish precipitate.
2K2MnO4 + 2H2O ¾® 2MnO2 + 4KOH + 2[O]
2e– + 2H2O + MnO42– ¾® MnO2 + 4OH–
This type of behaviour is shown by KMnO4 itself in neutral medium.
3e– + 2H2O + MnO4– ¾® MnO2 + 4OH–
In alkaline or neutral medium KMnO4 shows following oxidising properties.
(a) It oxidises ethene to glycol.
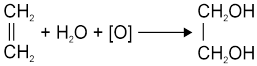
In alkaline medium KMnO4 solution is also known as Bayer’s reagent (1% alkaline KMnO4 solution).
(b) It oxidises iodide into iodate.
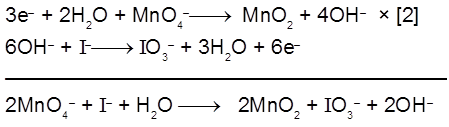
(c) H2S is oxidised into sulphur :
2MnO4– + 3H2S ¾® 2MnO2 + 2OH– +2H2O + 3S
(d) Manganous salt is oxidised to MnO2 ; the presence of zinc sulphate or zinc oxide catalyses the oxidation :
2MnO4– + 3Mn2+ + 2H2O ¾® 5MnO2 + 4H+
(e) In neutral/ faintly alkaline solution thiosulphate is quantitatively oxidised to sulphate.
8MnO4– + 3S2O32– + H2O ¾® 8MnO2 + 6SO42– + 2OH–
(f) In the presence of sodium hydroxide, sodium sulphite is oxidised in to sodium sulphate.
2MnO4– + 3SO32– + 3H2O ¾® 2MnO(OH)2¯+ 3SO42– + 2OH–.
In acidic medium (in presence of dilute H2SO4) :
Manganous sulphate is formed. The solution becomes colourless.
2KMnO4 + 3H2SO4 ¾® K2SO4 + 2MnSO4 + 3H2O + 5[O]
or MnO4¯ + 8H+ + 5e– ¾® Mn2+ + 4H2O
This medium is used in quantitative (volumetric) estimations. The equivalent mass of KMnO4 in acidic medium is = 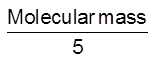 .
.
(a) Ferrous salts are oxidised to ferric salts.
MnO4¯ + 5Fe2+ + 8H+ ¾® 5Fe3+ + Mn2+ + 4H2O
(b) Iodine is evolved from potassium iodide.
2MnO4¯ + 10I¯ + 16H+ ¾® 2Mn2+ + 5I2 + 8H2O
(c) H2S is oxidised to sulphur :
2MnO4– + 16H++ 5S2– ¾® 2Mn2+ + 8H2O + 5S
(d) SO2 is oxidised to H2SO4 :
2MnO4– + 5SO2 + 2H2O ¾® 5SO42– + 2Mn2+ + 4H+
(e) Nitrites are oxidised to nitrates :
2MnO4– + 5NO2– + 6H+ ¾® 2Mn2+ + 3H2O + 5NO3–
(f) Oxalic acid is oxidised to CO2 :
This reaction is slow at room temperature, but is rapid at 60ºC.
Mn(II) ions produced catalyse the reaction; thus the reaction is autocatalytic.
2MnO4– + 16H+ + 5C2O42–![]() 2Mn2+ + 8H2O + 10CO2
2Mn2+ + 8H2O + 10CO2
(g) HCHO is oxidised to HCOOH
2MnO4– + 5HCHO + 6H+ ¾® 2Mn2+ + 5HCOOH + 3H2O.
(h) It oxidises hydrogen halides (HCl, HBr or HI) into X2 (halogen)
2MnO4– + 16H+ + 10X– ¾® 2Mn2+ + 8H2O + 5X2
(i) H2O2 is oxidised to O2.
2MnO4– + 6H+ + 5H2O2 ¾® 5O2 + Mn2+ + 8H2O.
Uses :It is used
- KMnO4 is used as an oxidising agent in laboratory and industry.
- Alkaline potassium permanganate is called Bayer's reagent. This reagent is used in organic chemistry for the test of unsaturation. KMnO4 is used in the manufacture of saccharin, benzoic acid, acetaldehyde etc.
- KMnO4 is used in qualitative analysis for detecting halides, sulphites, oxalates, etc.
4. POTASSIUM DICHROMATE
- Books Name
- ACME SMART COACHING Chemistry Book
- Publication
- ACME SMART PUBLICATION
- Course
- CBSE Class 12
- Subject
- Chemistry
POTASSIUM DICHROMATE (K2Cr2O7)
Preparation :
The chromite ore is roasted with sodium carbonate in presence of air in a reverberatory furnace.
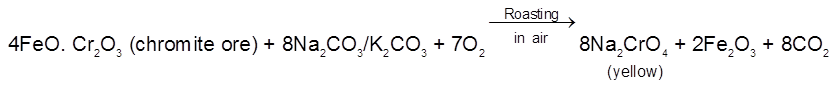
The roasted mass is extracted with water when Na2CrO4 goes into the solution leaving behind
insoluble Fe2O3. The solution is then treated with calculated amount of H2SO4.
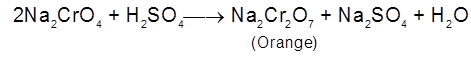
The solution is concentrated when less soluble Na2SO4 crystallises out. The solution is further concentrated when crystals of Na2Cr2O7 are obtained. Hot saturated solution of Na2Cr2O7 is then treated with KCl when orange red crystals of K2Cr2O7 are obtained on crystallisation. Sodium dichromate is more soluble than potassium dichromate.
Na2Cr2O7 + 2KCI ¾® K2Cr2O7 + 2 NaCl
K2Cr2O7 is preferred over Na2Cr2O7 as a primary standard in volumetric estimation because Na2Cr2O7 is
hygroscopic in nature but K2Cr2O7 is not.
Properties
(a) Physical :
It is orange-red coloured crystalline compound. It is moderately soluble in cold water but freely soluble in hot water. It melts at 398°C.
Structure of Chromate and Dichromate ion
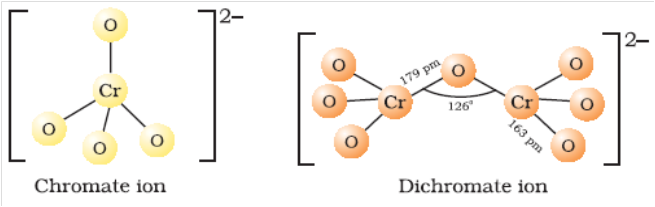
(b) Chemical :
(i) Effect of heating :
On heating strongly, it decomposes liberating oxygen.
2K2Cr2O7 ¾® 2K2CrO4 + Cr2O3 + ![]() O2
O2
On heating with alkalies, it is converted to chromate, i.e., the colour changes from orange to yellow. On acidifying, yellow colour again changes to orange.
K2Cr2O7 + 2KOH ¾® 2K2CrO4 + H2O
Cr2O72-(Orange) + 2OH¯ ¾® 2CrO42- (Yellow)+ H2O
2CrO(Yellow) + 2H+ ¾® Cr2O72- (Orange) + H2O
Thus CrO42– and Cr2O72– exist in equilibrium and are interconvertable by altering the pH of solution.
2CrO42- + 2H+![]() 2HCrO4–
2HCrO4–![]() Cr2O72- + H2O
Cr2O72- + H2O
In alkaline solution, chromate ions are present while in acidic solution, dichromate ions are present.
(ii) K2Cr2O7 + 2H2SO4 (conc. & cold) ¾® 2CrO3¯ (bright orange/red) + 2KHSO4 + H2O
2K2Cr2O7 + 8H2SO4 (conc. & Hot) ¾® 2K2SO4 + 8H2O + 2Cr2(SO4)3 + 3O2
(iii) Acidified K2Cr2O7 solution reacts with H2O2 to give a deep blue solution due to the formation of CrO5.
Cr2O72– + 2H+ + 4H2O2 ¾® 2CrO5 + 5H2O
Blue colour in aqueous solution fades away slowly due to the decomposition of CrO5 to Cr3+ ions and oxygen. In less acidic solution K2Cr2O7 and H2O2 give salt which is violet coloured and diamagnetic due to the formation of [CrO(O2)(OH)]–.
(iv)Potassium dichromate reacts with hydrochloric acid and evolves chlorine gas.
K2Cr2O7 + 14HCl ¾® 2KCl + 2CrCl3 + 7H2O + 3Cl2
(v) It acts as a powerful oxidising agent in acidic medium (dilute H2SO4)
Cr2O72- + 14H+ + 6e– ¾® 2Cr+3 + 7H2O. (Eº = 1.33 V)
The oxidation state of Cr changes from + 6 to +3.
(a) Iodine is liberated from potassium iodide :
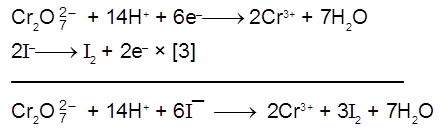
(b) Ferrous salts are oxidised to ferric salts :
6Fe2+ + Cr2O72- + 14H+ ¾® 6Fe3+ + 2Cr3+ + 7H2O
(c) Sulphites are oxidised to sulphates :
Cr2O72- + 3SO32- + 8H+¾® 3SO42- + 2Cr3+ + 4H2O
(d) H2S is oxidised to sulphur :
Cr2O72- + 3H2S + 8H+ ¾® 2Cr3+ + 7H2O + 3S
(e) SO2 is oxidised to H2SO4 :
Cr2O72– + 3SO2 + 2H+ ¾® 2Cr3+ + 3SO42– + H2O ;
Chrome alum is obtained when acidified K2Cr2O7 solution is saturated with SO2.
K2Cr2O7 + H2SO4 + 3SO2 + 23H2O ![]() K2SO4 . Cr2(SO4)3 . 24H2O
K2SO4 . Cr2(SO4)3 . 24H2O
(f) It oxidises ethylalcohol to acetaldehyde and acetaldehyde to acetic acid
C2H5OH ![]() CH3CHO
CH3CHO ![]() CH3COOH
CH3COOH
ethyl alcohol acetaldehyde acetic acid
(g) It also oxidises nitrites to nitrates, arsenites to arsenates, HBr to Br2. HI to I2, etc.
(h) K2Cr2O7 + 2C (charcoal) ![]() Cr2O3 + K2CO3 + CO ↑
Cr2O3 + K2CO3 + CO ↑
(vi) Chromyl chloride test :
4Cl– + Cr2O72– + 6H+ ¾® 2CrO2Cl2 ↑ (deep red) + 3H2O
CrO2Cl2 + 4OH– ¾® CrO42– (yellow) + 2Cl– + 2H2O
CrO42– (yellow) + Pb2+ ¾® PbCrO4 ↓ (yellow)
(vii) Cr2O72– (concentrated solution) + 2Ag+ ¾® Ag2Cr2O7↓ (reddish brown)
Ag2Cr2O7 ↓ + H2O ![]() Ag2CrO4 ↓+ CrO42– + 2H+ .
Ag2CrO4 ↓+ CrO42– + 2H+ .
(viii) Cr2O72– + Ba2+ + H2O ![]() 2BaCrO4 ↓+ 2H+
2BaCrO4 ↓+ 2H+
As strong acid is produced, the precipitation is only partial. But if NaOH or CH3COONa is added, precipitate becomes quantitative.
Uses : It is used :
(i) as a volumetric reagent in the estimation of reducing agents such as oxalic acid, ferrous ions, iodide ions, etc. It is used as a primary standard.
(ii) for the preparation of several chromium compounds such as chrome alum, chrome yellow, chrome red, zinc yellow, etc.
(iii) in dyeing, chrome tanning, calico printing, photography etc.
(iv) as a cleansing agent for glass ware in the form of chromic acid.
in leather industry and as an oxidant for preparation of azo compounds.
5. Periodic trends and properties of f-Block Elements
- Books Name
- ACME SMART COACHING Chemistry Book
- Publication
- ACME SMART PUBLICATION
- Course
- CBSE Class 12
- Subject
- Chemistry
Periodic trends and properties of f-Block Elements
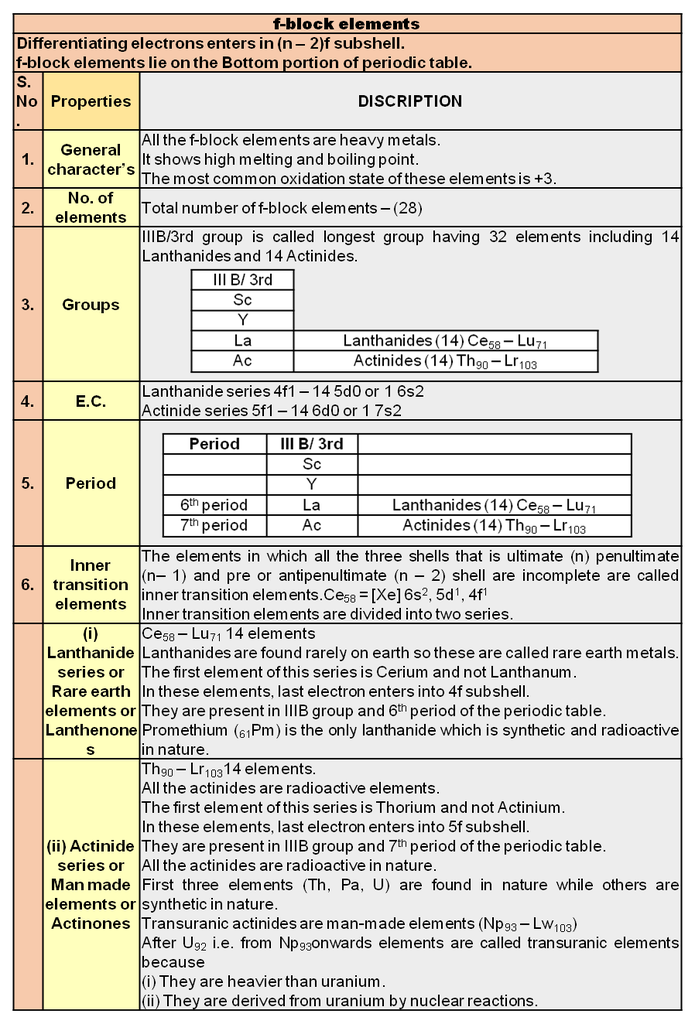
6. The Lanthanides
- Books Name
- ACME SMART COACHING Chemistry Book
- Publication
- ACME SMART PUBLICATION
- Course
- CBSE Class 12
- Subject
- Chemistry
The Lanthanides
The names, symbols, electronic configurations of atomic and some ionic states and atomic and ionic radii of lanthanum and lanthanide (for which the general symbol Ln is used) are given in Table.
Electronic Configurations : It may be noted that atoms of these elements have electronic configuration with 6s2 common but with variable occupancy of 4f level (Table). However, the electronic configurations of all the tripositive ions (the most stable oxidation state of all the lanthanides) are of the form 4fn (n = 1 to 14 with increasing atomic number).
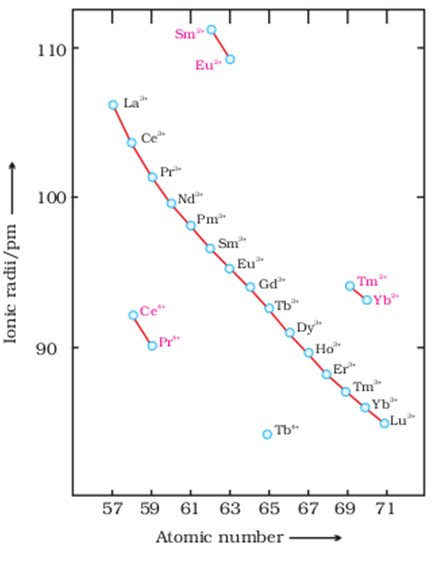
Atomic and Ionic Sizes : The overall decrease in atomic and ionic radii from lanthanum to lutetium (the lanthanide contraction). The shielding of one 4 f electron by another is less than one d electron by another with the increase in nuclear charge along the series. There is fairly regular decrease in the sizes with increasing atomic number. The cumulative effect of the contraction of the lanthanide series, known as lanthanide contraction, causes the radii of the members of the third transition series to be very similar to those of the corresponding members of the second series. The almost identical radii of Zr (160 pm) and Hf (159 pm), a consequence of the lanthanide contraction.
Oxidation States : In the lanthanides, La(III) and Ln(III) compounds are predominant species. However, occasionally +2 and +4 ions in solution or in solid compounds are also obtained.
This irregularity (as in ionisation enthalpies) arises mainly from the extra stability of empty, half-filled or filled f subshell. Thus, the formation of CeIV is favoured by its noble gas configuration, but it is a strong oxidant reverting to the common +3 state. The EΘ value for Ce4+/ Ce3+ is + 1.74 V which suggests that it can oxidise water. However, the reaction rate is very slow and hence Ce(IV) is a good analytical reagent.
Pr, Nd, Tb and Dy also exhibit +4 state but only in oxides, MO2. Eu2+ is formed by losing the two s electrons and its f7 configuration accounts for the formation of this ion.
However, Eu2+ is a strong reducing agent changing to the common +3 state. Similarly Yb2+ which has f 14 configuration is a reductant.
TbIV has half-filled f-orbitals and is an oxidant. The behaviour of samarium is very much like europium, exhibiting both +2 and +3 oxidation states.
General Characteristics :
All the lanthanides are silvery white soft metals and tarnish rapidly in air.
The hardness increases with increasing atomic number, samarium being steel hard.
Their melting points range between 1000 to1200K but samarium melts at 1623 K.
They have typical metallic structure and are good conductors of heat and electricity. Density and other properties change smoothly except for Eu and Yb and occasionally for Sm and Tm.
Many trivalent lanthanide ions are coloured both in the solid state and in aqueous solutions. Colour of these ions may be attributed to the presence of f electrons. Neither La3+ nor Lu3+ ion shows any colour but the rest do so. However, absorption bands are narrow, probably because of the excitation within f level.
The lanthanide ions other than the f°type (La3+ and Ce4+) and the f14 type (Yb2+ and Lu3+) are all paramagnetic. The paramagnetism rises to maximum in neodymium.
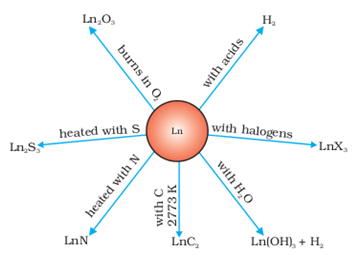
The first ionisation enthalpies of the lanthanides are around 600 kJ mol–1, the second about 1200 kJ mol–1 comparable with those of calcium.
A detailed discussion of the variation of the third ionisation enthalpies indicates that the exchange enthalpy consideration (as in 3d orbitals of the first transition series), appear to impart a certain degree of stability to empty, half-filled and completely filled orbitals f level. This is indicated from the abnormally low value of the third ionization enthalpy of lanthanum, gadolinium and lutetium.
In their chemical behaviour, in general, the earlier members of the series are quite reactive similar to calcium but, with increasing atomic number, they behave more like aluminium.
Values for E– for the half-reaction:
Ln3+ (aq) + 3e−→ Ln(s) are in the range of –2.2 to –2.4 V except for Eu for which the value is – 2.0 V. This is, of course, a small variation.
The metals combine with hydrogen when gently heated in the gas.
The carbides, Ln3C, Ln2C3 and LnC2 are formed when the metals are heated with carbon.
They liberate hydrogen from dilute acids and burn in halogens to form halides.
They form oxides M2O3 and hydroxides M(OH)3. The hydroxides are definite compounds, not just hydrated oxides.
They are basic like alkaline earth metal oxides and hydroxides.
The best single use of the lanthanides is for the production of alloy steels for plates and pipes. A well known alloy is mischmetall which consists of a lanthanide metal (~ 95%) and iron (~ 5%) and traces of S, C, Ca and Al. A good deal of mischmetall is used in Mg-based alloy to produce bullets, shell and lighter flint. Mixed oxides of lanthanides are employed as catalysts in petroleum cracking. Some individual Ln oxides are used as phosphors in television screens and similar fluorescing surfaces.
7. The Actinides
- Books Name
- ACME SMART COACHING Chemistry Book
- Publication
- ACME SMART PUBLICATION
- Course
- CBSE Class 12
- Subject
- Chemistry
The Actinides
The actinides include the fourteen elements from Th to Lr. The names, symbols and some properties of these elements are given in Table.
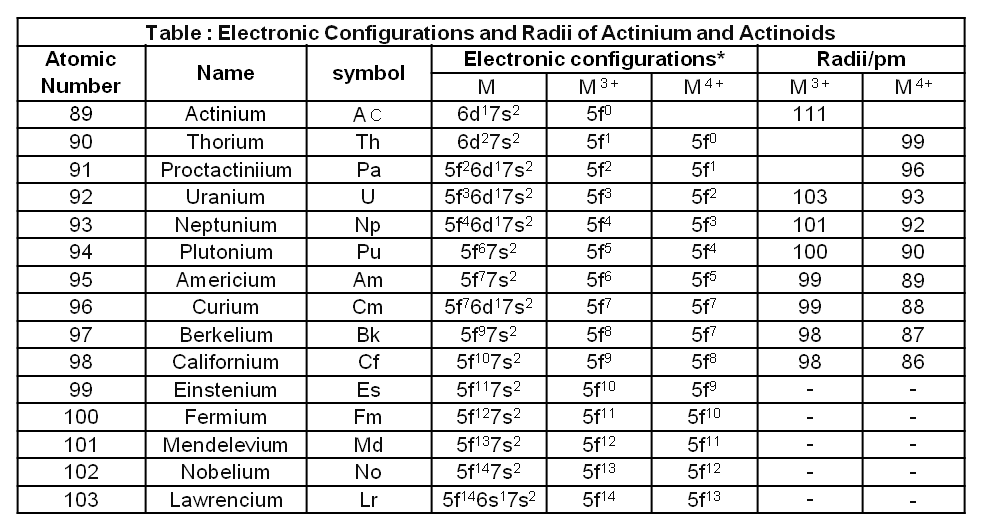
The actinides are radioactive elements and the earlier members have relatively long half-lives, the latter ones have half-life values ranging from a day to 3 minutes for lawrencium (Z =103). The latter members could be prepared only in nanogram quantities. These facts render their study more difficult.
Electronic Configurations :
All the actinides are believed to have the electronic configuration of 7s2 and variable occupancy of the 5f and 6d subshells.
The fourteen electrons are formally added to 5f, though not in thorium (Z = 90) but from Pa onwards the 5f orbitals are complete at element 103.
The irregularities in the electronic configurations of the actinides, like those in the lanthanides are related to the stabilities of the f° , f7 and f14 occupancies of the 5f orbitals. Thus, the configurations of Am and Cm are [Rn] 5f77s2 and [Rn] 5f7 6d1 7s2 .
Although the 5f orbitals resemble the 4f orbitals in their angular part of the wave-function, they are not as buried as 4f orbitals and hence 5f electrons can participate in bonding to a far greater extent.
Ionic Sizes :
The general trend in lanthanides is observable in the actinides as well. There is a gradual decrease in the size of atoms or M3+ ions across the series. This may be referred to as the actinide contraction (like lanthanide contraction). The contraction is, however, greater from element to element in this series resulting from poor shielding by 5f electrons.
Oxidation States :
There is a greater range of oxidation states, which is in part attributed to the fact that the 5f, 6d and 7s levels are of comparable energies. The known oxidation states of actinides are listed in Table.
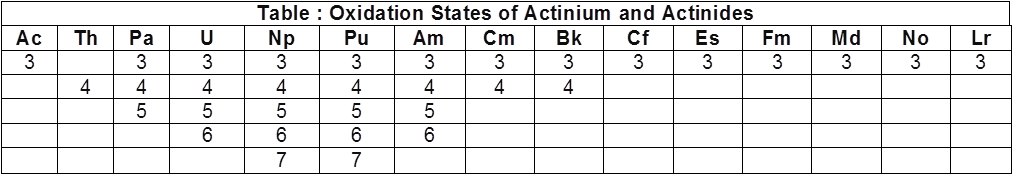
The actinides show in general +3 oxidation state.
The elements, in the first half of the series frequently exhibit higher oxidation states. For example, the maximum oxidation state increases from +4 in Th to +5, +6 and +7 respectively in Pa, U and Np but decreases in succeeding elements.
The actinides resemble the lanthanides in having more compounds in +3 state than in the +4 state. However, +3 and +4 ions tend to hydrolyse.
Because the distribution of oxidation states among the actinides is so uneven and so different for the earlier and latter elements, it is unsatisfactory to review their chemistry in terms of oxidation states.
General Characteristics and Comparison with Lanthanides :
The actinide metals are all silvery in appearance but display a variety of structures. The structural variability is obtained due to irregularities in metallic radii which are far greater than in lanthanides.
The actinides are highly reactive metals, especially when finely divided. The action of boiling water on them, for example, gives a mixture of oxide and hydride and combination with most non metals takes place at moderate temperatures. Hydrochloric acid attacks all metals but most are slightly affected by nitric acid owing to the formation of protective oxide layers; alkalies have no action.
The magnetic properties of the actinides are more complex than those of the lanthanides. Although the variation in the magnetic susceptibility of the actinides with the number of unpaired 5 f electrons is roughly parallel to the corresponding results for the lanthanides, the latter have higher values.
It is evident from the behaviour of the actinides that the ionisation enthalpies of the early actinides, though not accurately known, but are lower than for the early lanthanides. This is quite reasonable since it is to be expected that when 5f orbitals are beginning to be occupied, they will penetrate less into the inner core of electrons. The 5f electrons, will therefore, be more effectively shielded from the nuclear charge than the 4f electrons of the corresponding lanthanides. Because the outer electrons are less firmly held, they are available for bonding in the actinides.
A comparison of the actinides with the lanthanides, with respect to different characteristics as discussed above, reveals that behaviour similar to that of the lanthanides is not evident until the second half of the actinide series. However, even the early actinides resemble the lanthanides in showing close similarities with each other and in gradual variation in properties which do not entail change in oxidation state. The lanthanide and actinide contractions, have extended effects on the sizes, and therefore, the properties of the elements succeeding them in their respective periods. The lanthanide contraction is more important because the chemistry of elements succeeding the actinides are much less known at the present time.
7. General characteristics of catalyst
- Books Name
- ACME SMART COACHING Chemistry Book
- Publication
- ACME SMART PUBLICATION
- Course
- CBSE Class 12
- Subject
- Chemistry
General characteristics of catalyst
A catalyst does not initiate the reaction. It simply fastens it.
Only a small amount of catalyst can catalyse the reaction.
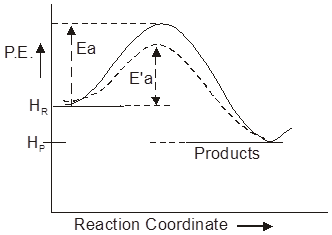
A catalyst does not alter the position of equilibrium i.e. magnitude of equilibrium constant and hence DGº. It simply lowers the time needed to attain equilibrium. This means if a reversible reaction in absence of catalyst completes to go to the extent of 75% till attainment of equilibrium, and this state of equilibrium is attained in 20 minutes then in presence of a catalyst also the reaction will go to 75% of completion before the attainment of equilibrium but the time needed for this will be less than 20 minutes.
A catalyst drives the reaction through a low energy path and hence Ea is less. That is, the function of the catalyst is to lower down the activation energy.
Ea = Energy of activation in absence of catalyst.
E’a = Energy of activation in presence of catalyst.
Ea – E’a = lowering of activation energy by catalyst.
Comparision of rates of reaction in presence and absence of catalyst :
If k and kcat be the rate constant of a reaction at a given temperature T, and Ea and E’a are the activation energies of the reaction in absence and presence of catalyst, respectively, the
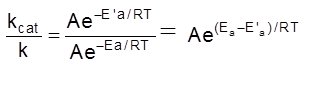
Derivation of a suitable rate law with the help of a suitable mechanism :
Molecularity and Order :
The number of molecules that react in an elementary step is the molecularity of the elementary reaction. Molecularity is defined only for the elementary reactions and not for complex reactions.
No elementary reactions involving more than three molecules are known, because of very low probability of near-simultaneous collision of more than three molecules.
The rate law for the elementary reaction
aA + bB¾® products
rate = k[A]a[B]b, where a + b = 1, 2 or 3.
For an elementary reaction, the orders in the rate law equal the coefficients of the reactants.
While, the order is defined for complex as well as elementary reactions and is always experimentally calculated by the mechanism of the reaction, usually by the slowest step of the mechanism known as rate determining step of the reaction.

Mechanism of a reaction :
Reactions can be divided into
Elementary / simple / single step
Complex / multi-step
ELEMENTARY REACTION :
These reaction take place in single step without formation of any intermediate
For elementary reaction we can define molecularity of the reaction which is equal to no of molecules which make transition state or activated complex because of collisions in proper orientation and with sufficient energy
molecularity will always be a natural no
1 = unimolecular one molecule gets excited (like radioectivity)
2.= bimolecular
3 = trimolecular
Molecularly 3 because the probabilty of simaltaneous collision between 4 or more molecules in proper orientation is very low. For elementary reaction there is only single step and hence it is going to be rate determining step so order of an elementary reaction is its molecularity
Order of elementary reaction w.r.t. reactant = stoichiometric co-efficient of the reactant
H2 + I2 ![]() 2HI ® Simple reaction rate = k [H2] [I2]
2HI ® Simple reaction rate = k [H2] [I2]
2H2 + 2I2 ![]() 4HI (not elementary )
4HI (not elementary )
reaction obtained by multiplying an elementary reaction with some no will not be of elementary nature
H2 + Cl2 ![]() 2HCl order = 0
2HCl order = 0
COMPLEX REACTION :
Reaction which proceed in more than two steps. or having some mechanism. ( sequence of elementary reaction in which any complex reaction procceds)
For complex reaction each step of mechanism will be having its own molecularity but molecularity of net complex reaction will not be defined.
Order of complex reaction can be zero fractions whole no, even negative w.r.t. some species.
Order of reaction or rate law of reaction is calculated with the help of mechanism of the reaction generally using Rate determine step (R.D.S) if given.
Rate law of a reaction is always written in terms of conc. of reactant, products or catalysts but never in terms of conc. of interimediates.
The mechanism of any complex recation is always written in terms of elementary steps, so molecularity of each of these steps will be defined but net molecularity of complex reaction has no meaning.
The mechanism of most of the reaction will be calculated or predicted by using mainly the following approximations.
COMPLICATIONS IN 1ST ORDER REACTION
PARALLEL 1st ORDER REACTION
Frequently a species can react in different ways to give a variety of products. For example, toluene can be nitrated at the ortho, meta, or para positions, We shall consider the simplest case, that of two competing irreversible first-order reactions :
A ![]() B and A
B and A![]() C
C
where the stoichiometric coefficients are taken as unity for simplicity. The rate law is
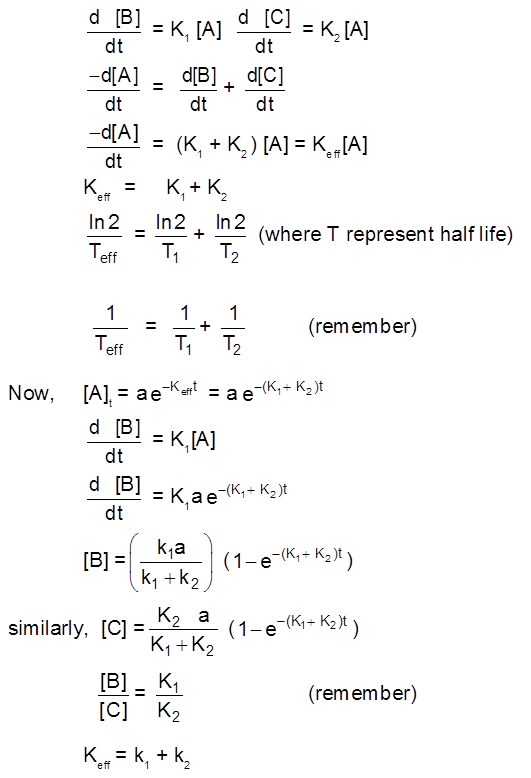
3. Colligative properties & constitutional properties
- Books Name
- ACME SMART COACHING Chemistry Book
- Publication
- ACME SMART PUBLICATION
- Course
- CBSE Class 12
- Subject
- Chemistry
Colligative properties & constitutional properties :
Constitutional Properties : Properties which are dependent on nature of particles are constitutional properties like electrical conductance.
Colligative properties : The properties of the solution which are dependent only on the total no. of particles relative to solvent/solution or total concentration of particles in the solution and are not dependent on the nature of particle i.e. shape, size, neutral /charge etc. of the particles.
There are 4 colligative properties of solution :
Osmotic pressure
Relative lowering in vapour pressure ![]()
Elevation in b.p. (DTb)
Depression in freezing pt. (DTf)
(i) Osmosis & Osmotic pressure :
Osmosis: The spontaneous flow of solvent particles from solvent side to solution side or from solution of low concentration side to solution of high concentration side through a semipermeable membrane (SPM) is known as osmosis.
Ex.

Conclusion : After some time in (A) grape or egg will shrink and in (B) grape or egg will swell.
e.g. (i) A raw mango placed in concentrated salt solution loses water & shrivel into pickle.
(ii) People taking lot of salt, experience water retention in tissue cells. This results in puffiness or swelling called edema.
Biological Importance of Osmosis
The cell walls of plants and animals are semipermeable in nature and thus are responsible for the osmosis. When a cell comes in contact with water a tendency of flow of water into the cell is developed. The pressure developed inside the cell due to the inflow of water is called turgor.
If the cell comes in contact with a concentrated solution, cell would shrink, which is called plasmolysis. Cell walls are able to permit the flow of selected ions and molecules also along with water.
Various processes taking place due to osmosis are :
(a) Absorption of water from soil through the cell walls of roots.
(b) Movement of water from roots to the upper parts of plants & trees.
(c) Various types of locomotion in plants like stretching of leaves, opening of flowers, etc., are also based on osmosis.
(d) Germination is also caused due to osmosis as water moves into the seeds through cell walls.
The phenomenon of osmosis : A solution inside the bulb is separated from pure solvent in the beaker by a semipermeable membrane, Net passage of solvent from the beaker through the memberane occurs, and the liquid in the tube rises untill equilibrium is reached. At equilibrium, the osmotic pressure exerted by the column liquid in the tube is sufficient to prevent further net passage of solvent.
Although the passage of solvent through the membrane takes place in both direction, passage from the pure solvent side to the solution side is more favoured and occurs faster. As a result, the amount of liquid on the pure solvent side decreases, the amount of liquid on the solution side increases, and the concentration of the solution decreases.
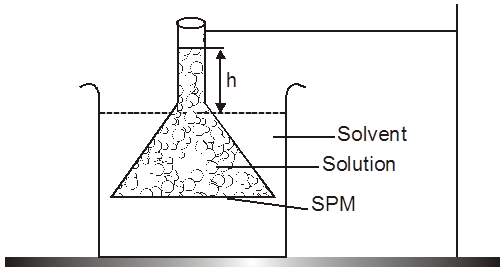
Osmotic Pressure : The equilibrium hydrostatic pressure developed by solution column when it is seperated from solvent by semipermeable membrane is called O.P. of the solution.
p = rgh ;
r = density of soln.
g = acceleration due to gravity;
h = eq. height
1 atm = 1.013 x 105 N/m2
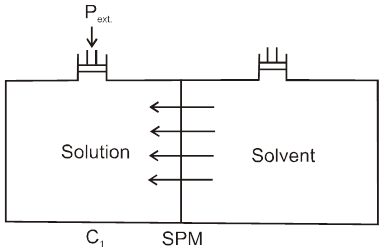
Definition : The external pressure which must be applied on solution side to stop the process of osmosis is called osmotic pressure of the solution.
If two solutions of concentration C1 and C2 are kept separated by SPM, and C1 > C2 then particle movement take place from lower to higher concentration. So, extra pressure is applied on higher concentration side to stop osmosis. And
Pext. = (p1 – p2)
Reverse Osmosis : If the pressure applied on the solution side is more than osmotic pressure of the solution then the solvent particles will move from solution to solvent side. This process is known as reverse osmosis.
Berkely : Hartely device/method uses the above pressure to measure osmotic pressure.
e.g. used in desalination of sea-water.
Vant – Hoff Formula (For calculation of osmotic pressure)
p a concentration (molarity)
a T
p = CST
S = ideal solution constant p = atm. 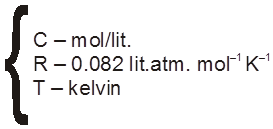
= 8.314 J mol–1 K–1 (exp value)
= R (ideal gas) constant
p = CRT = ![]() RT (just like ideal gas equation)
RT (just like ideal gas equation)
In ideal solution solute particles can be assumed to be moving randomly without any interactions.
 C = total concentration of all types of particles.
C = total concentration of all types of particles.
= C1 + C2 + C3 + s.................
= ![]()
Type of solutions :
(a) Isotonic solution : Two solutions having same osmotic pressure are consider as isotonic solution.
p1 = p2 (at same temperature)
(b) Hypotonic & Hypertonic solutions : If two solutions 1 and 2 are such that p2 > p1 , then 2 is called hypertonic solution and 1 is called hypotonic solution.
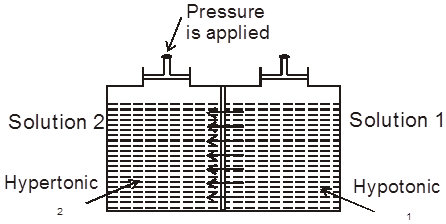
Conclusion :Pressure is applied on the hypertonic solution to stop the flow of solvent partices, this pressure become equal to (p2 – p1) and if hypotonic solution is replaced by pure solvent then pressure becomes equal to p2.
Note : Osmotic pressure of very dilute solutions is also quite significant. So, its measurement in lab is very easy.
Plasmolysis : When the cell is placed in solution having osmotic pressure greater than that of the cell sap, water passes out of the cell due to osmosis. Consequently, cell material shrinks gradually. The gradual shrinking of the cell material is called plasmolysis.
Abnormal Colligative Properties : [Vant–Hoff correction :]
For electrolytic solutes the number of particles would be different from the number of particles actually added, due to dissociation or association of solute.
The actual extent of dissociation/association can be expressed with a correction factor known as vant Haff factor (i).
Vant–Hoff factor : i =![]()
If solute gets associated or dissociated in solution then experimental / observed / actual value of colligative property will be different from theoretically predicted value so it is also known as abnormal colligative property.
This abnormality can be calculated in terms of Vant-Hoff factor.
i=![]() =
=![]() =
= ![]()
i > 1 dissociation
i < 1 association
i = ![]()
Modified formula \ p= iCRT
p= (i1C1 + i2C2 + i3C3.....) RT
Case - I : Electrolyte dissociates
Relation between i & (degree of dissociation) :
Let the electrolyte be AxBy
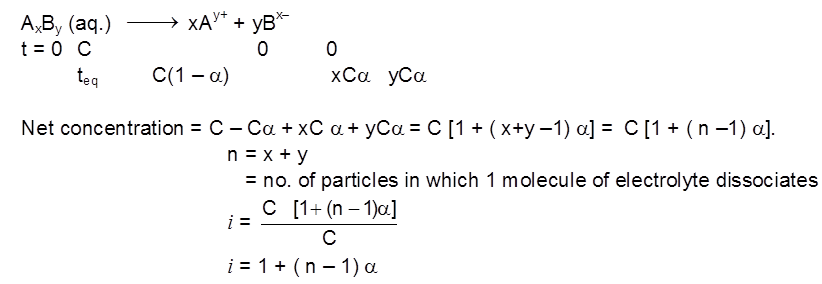
e.g. NaCl (100% ionised), i = 2. ; BaCl2 (100% ionised), i = 3. ; K4[Fe(CN)6] (75% ionised), i = 4.
Case - II : Electrolyte associates
Relation between degree of association b & i.
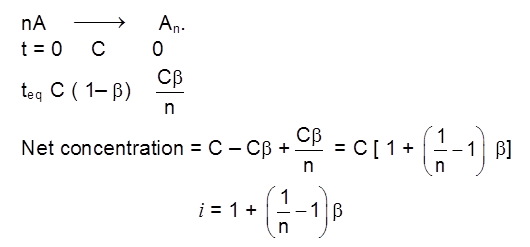
if dimerise n = 2 ; trimerise n = 3 ; tetramerise n = 4.
e.g. CH3COOH 100% dimerise in benzene, i = ![]() ; C6H5COOH 100% dimerise in benzene, i =
; C6H5COOH 100% dimerise in benzene, i = ![]()
(ii) Relative lowering in vapour pressure ( RLVP) :
Vapour Pressure :
The conversion of a liquid to a vapour takes place in a
visible way when the liquid boils, it takes place under all conditions.
say 5 gm liquid left at teq
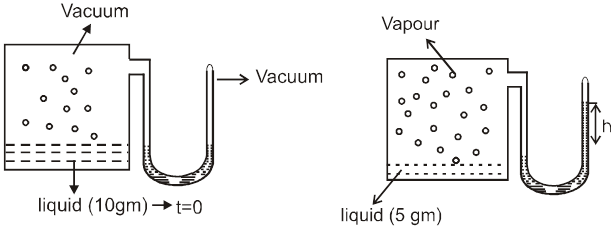
At eq. : the rate of evaporation = rate of condense
H2 O (λ) ![]() H2 O (g)
H2 O (g)
Kp = ![]() eq.
eq.
finally
The pressure exerted by vapours of the liquid when equilibrium is established between vapours & its liquid. is known as vapour pressure.
Vapour pressure is an equilibrium constant (KP) of the reaction.
liquid ![]() vapours.
vapours.
Since vapour pressure is an equilibrium constant so its value is dependent only on temperature for a particular liquid
It does not depends on the amount of liquid taken or surface area of the liquid or on volume or shape of the container. It is a characteristic constant for a given liquid.
Vapour Pressure of a solution
Vapour Pressure of a solutions of a non volatile solute ( solid solute ) is always found to be less than the vapour pressure of pure solvent .
Reason : Some of the solute molecules will occupy some surface area of the solutions so tendency of the solvent particles to go into the vapour phase is slightly decreased hence Pº > PS, where Pº is vapour pressure of pure solvent and PS is vapour pressure of the solution.
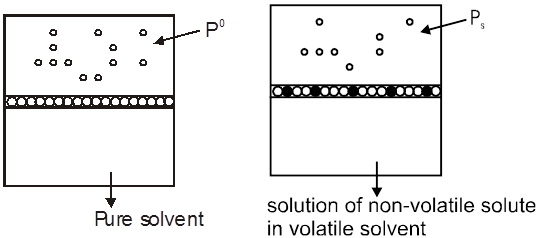
Lowering in VP = Pº – PS = DP
and Relative lowering in Vapour Pressure = ![]()
Raoult's law (For non–volatile solutes): The vapour pressure of a solution of a non-volatile solute is equal to the vapour pressure of the pure solvent at that temperature multiplied by its mole fraction.
OR Relative Lowering in Vapour Pressure = mole fraction of the non volatile solute in solution
.![]()
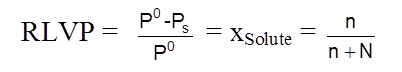
where n = number of moles of non-volatile solute and N = number of moles of solvent in the solution.
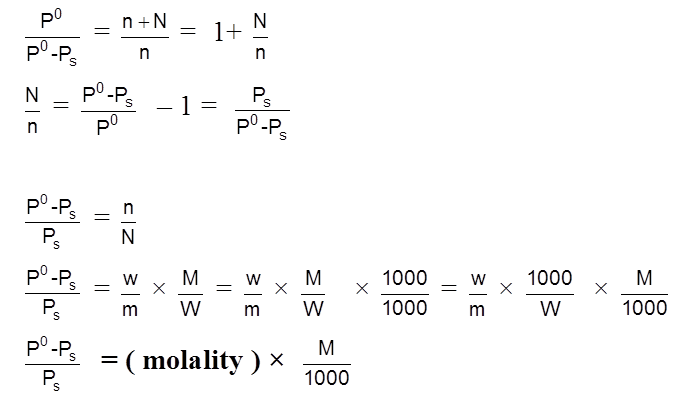
where w and W = mass of non-volatile solute and volatile solvent respectively
m and M = molar mass of non-volatile solute and volatile solvent respectively
If solute gets associated or dissociated ;
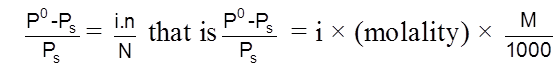
(iii) Elevation in Boiling point (DTb)
Boiling point of a Liquid : The temprature at which vapour pressure of a liquid becomes equal to the external pressure present at the surface of the liquid is called b.p of liquid at that pressure.
Normal boiling point : The temperature at which boiling ocuurs when the external pressure is exactly 1 atm is called the normal boiling point of the liquid. (Tb)
Boiling pt of any solution :
Since V.P. of solution is smaller then v.p. of pure solvent at any temperature hence to make it equal to Pext. we have to increase the temp. of solution by greater amount in comparision to pure solvent.
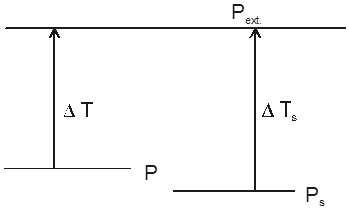
DHvapour of solvent =DHvapour solution
Graphical : 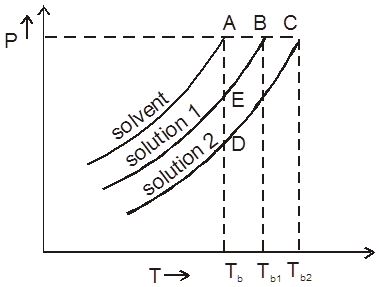
Using Raoult’s law :
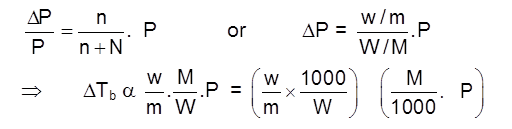
Tb = Kb × molality
Kb is dependent on property of solvent and known as molal elevation constant of solvent
It is also known as ebullioscopic constant.
Kb = elevation in boiling point of 1 molal solution.
Units : ![]() = K kg mol–1
= K kg mol–1
Using thermodynamics : Kb =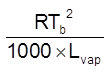
LVap – is latent heat of vapourization in cal/g or J/g
R = 2 cal mol–1 K–1 or 8.314 J mol–1 K–1. ; Tb = b.p. of liquid (in kelvin)
Kb = K kg mol–1
Also Kb = ![]()
Here:DHvap=molar enthalpy of vaporisation in cal/mole of J/mole
M Þ mole wt. of solvent
Lvap = 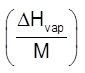
If solute gets associated/dissociated :DTb = i × Kb × molality
(iv) Depression in freezing pt (DTf)
Freezing point : Temperature at which vapour pressure of solid becomes equal to v.p of liquid is called freezing point of liquid or melting point of solid.
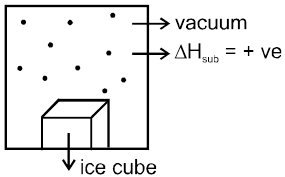
DHsub > DHvap.
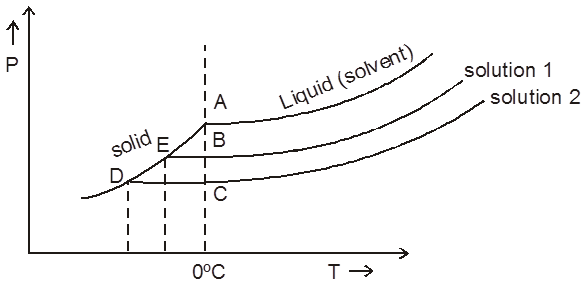
For - dil. solutions BE & CD can be assumed to be straight lines.
using similar triangles
\ DTf a P
\ DTf = Kf . Molality
Kf = molal depression constant = cryoscopic constant
Kf = 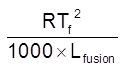 =
= 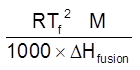
for water Tf = 273 K & LFusion = 80 cal / gm
Kf = ![]() = 1.86 K kg mol–1
= 1.86 K kg mol–1
At freezing point or below it only solvent molecules will freeze not solute molecules (solid will be of pure solvent)
8. Some applications of d-and f-Block elements
- Books Name
- ACME SMART COACHING Chemistry Book
- Publication
- ACME SMART PUBLICATION
- Course
- CBSE Class 12
- Subject
- Chemistry
Some Applications of d- and f-Block Elements
Iron and steels are the most important construction materials. Their production is based on the reduction of iron oxides, the removal of impurities and the addition of carbon and alloying metals such as Cr, Mn and Ni.
TiO for the pigment industry and MnO2 for use in dry battery cells. The battery industry also requires Zn and Ni/Cd.
The ‘silver’ UK coins are a Cu/Ni alloy.
1. Occurrence of metals
- Books Name
- ACME SMART COACHING Chemistry Book
- Publication
- ACME SMART PUBLICATION
- Course
- CBSE Class 12
- Subject
- Chemistry
Chapter 6
General principles and processes of isolation of elements
Introduction :
The compound of a metal found in nature is called a mineral. The minerals from which metal can be economically and conveniently extracted are called ores. An ore is usually contaminated with earthy or undesired materials known as gangue. So all minerals are not ores but all ores are minerals. Ores may be classified mainly into following four classes.
(a) Native ores : They contain the metal in free state. Silver, gold, platinum etc, occur as native ores.
(b) Oxidised ores : These ores consist of oxides or oxysalts (e.g. carbonates, phosphates, sulphates and silicates ) of metals.
(c) Sulphurised ores : These ores consist of sulphides of metals like iron, lead, zinc, mercury etc.
(d) Halide ores : These ores consist of halides of metals.
Important ore :
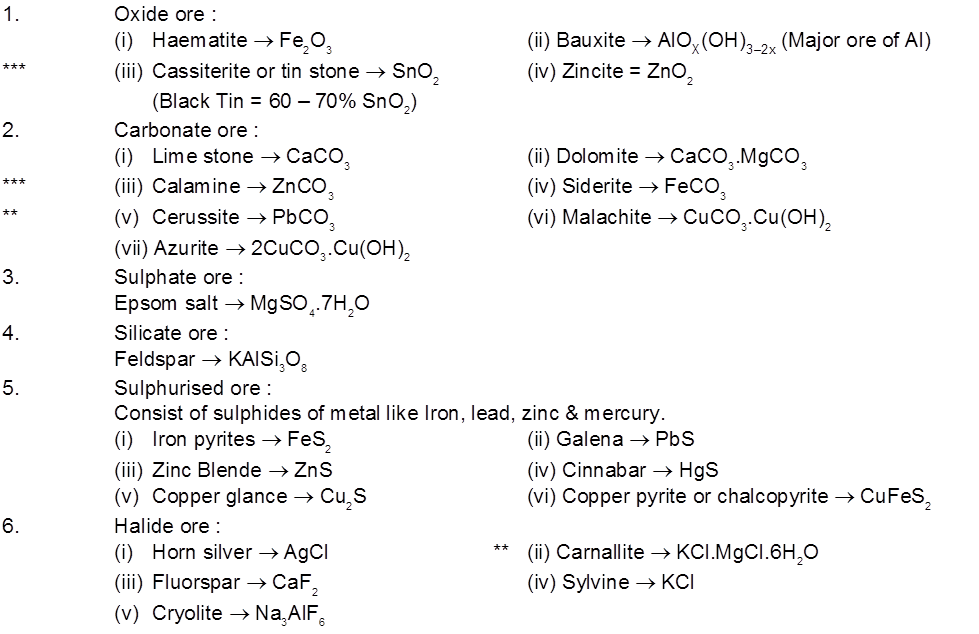
Note : Mg obtained from both sea water & earth crust.
Metallurgy :
The scientific and technological process used for the extraction/isolation of the metal from its ore is called as metallurgy.
The isolation and extraction of metals from their ores involve the following major steps:
(A) Crushing of the ore.
(B) Dressing or concentration of the ore.
(C) Isolation of the crude metal from its ore
(D) Purification or refining of the metal.
Chart1:
Chart2: Steps involved in metallurgy.
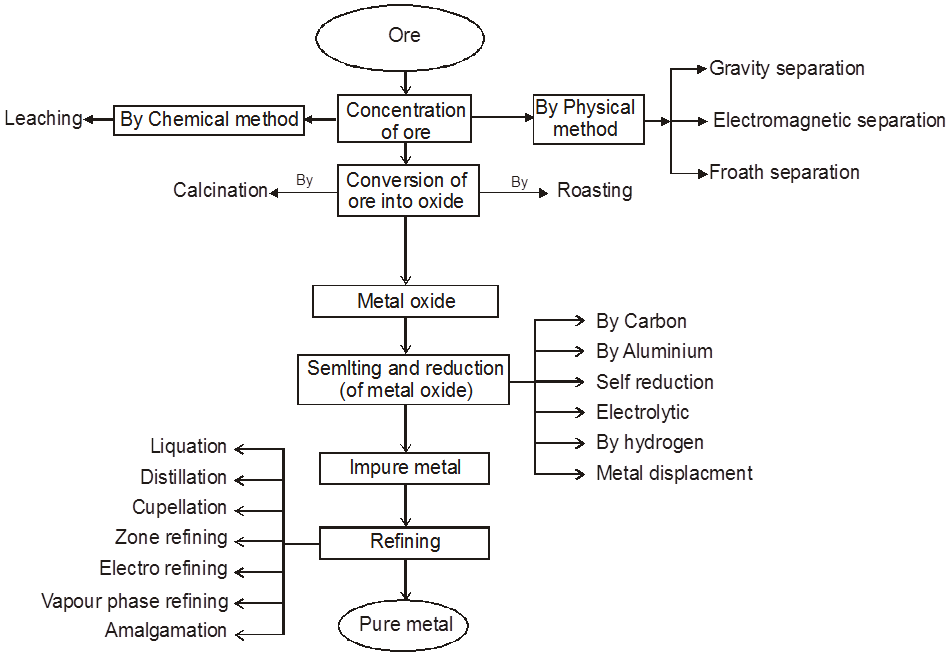
1. Physical Method :
(A) Crushing and Grinding : The ore is first crushed by jaw crushers and ground to a powder (pulverisation of the ore) in equipments like ball mills and stamp mills.
(B) Concentration : The removal of unwanted useless impurities from the ore is called dressing, concentration or benefaction of ore.
It involves several steps and selection of these steps depends upon the difference in physical properties of the compound of metal and that of gangue. Some of the important procedures are described below.
(i) Hydrolytic washing :
Gravity separation or "Levigation". Based on the difference in the densities of the gangue and ore particle.
Generally used for the concentration of oxide & native ore.
(ii) Electromagnetic sepration :
Based on difference in magnetic properties of mineral and gangue particle.
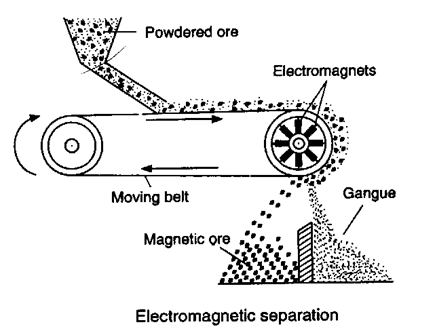
(a) Chromite ore [FeO.Cr2O3] is seprated from non magnetic silicious impurities.
(b) Cassiterite ore [SnO2] is seprated from magnetic wolframite [FeWO4 + MnWO4]
(iii) Froth floatation process :
Generally used for concentration of low grade sulphide ore PbS, ZnS, Cu2S, CuFeS2
Principle :
Based on fact that mineral & gangue particles have different wettability in water and oil (pine oil used)
Mineral particle ® are wetted by oil.
Gangue particle ® Wetted by water.
Reagents Used :
(i) Frothers :
These form stable froth which rises to the top of the flotation cell.
Oil like pine oil, comphor oil are used in small quantities.
Main Function of :
Frother ®Stick to ore & then take it to rise upto the top.
Stabilizer ® To stabilize the froth, froth stabilizer like [cresol & aniline] are added.
(ii) Collector :
K+ or Na+ ethyl xanthates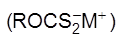 (R = alkyl,M+ = Na+ , K+) are used as collectors. Which collect or attract mineral partical and make them water repellant.
(R = alkyl,M+ = Na+ , K+) are used as collectors. Which collect or attract mineral partical and make them water repellant.
Main Function : Make the ore hydrophobic.
(iii) Activating & Depressing agents :
In PbS + ZnS + FeS2 mixture NaCN + Na2CO3 is used to depress the floation properties of ZnS & FeS2.
ZnS + CN– ¾® [Zn(CN)4]2–
FeS2 + CN– ¾® [Fe(CN)6]4–
CuSO4 is then added which is activating for ZnS as Cu forms more stable complexing with CN– than Zn2+
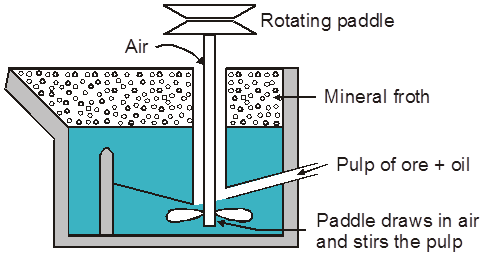
2. Chemical Method :
(4) Leaching :
Used when ore is soluble in some suitable solvent like ® acid, base & suitable chemical reagent.
Ex. (a) Leaching of alumina from bauxite.
(b) Extraction of Ag & Au from their ores in the complex form by treatment with NaCN & KCN.
(c) Treatment of low grade Cu ores with conc. H2SO4.
(C) Extraction of crude metal from concentrated ore :
The concentrated ore must be converted into a form which is suitable for reduction. Usually the sulphide ore is converted to oxide before reduction. Oxides are easier to reduce. Thus isolation of metals from concentrated ore involves two major steps as given below.
(i) Conversion to oxide
(ii) Reduction of the oxide to metal.
(i) Conversion to oxide :

Conversion of ore into oxide is carried out in two ways depending upon the nature of ore.
Calcination. It is a process of heating the concentrated ore strongly in a limited supply of air or in the absence of air. The process of calcination brings about the following changes :
(a) The carbonate ore gets decomposed to form the oxide of the metal, e.g.,
FeCO3 (siderite) 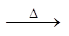 FeO + CO2
FeO + CO2
PbCO3 (cerrussite) 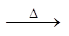 PbO + CO2
PbO + CO2
CaCO3 (calcite ore / lime stone) 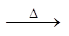 CaO + CO2
CaO + CO2
ZnCO3 (calamine) 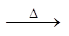 ZnO + CO2
ZnO + CO2
CuCO3.Cu(OH)2 (malachite) 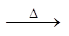 2CuO + H2O + CO2
2CuO + H2O + CO2
MgCO3.CaCO3 (dolomite) 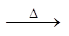 MgO + CaO + 2CO2
MgO + CaO + 2CO2
(b) Water of crystallisation present in the hydrated oxide ore gets lost as moisture, e.g.,
2Fe2O3.3H2O (limonite) 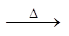 2Fe2O3(s) + 3H2O(g)
2Fe2O3(s) + 3H2O(g)
Al2O3. 2H2O (bauxite) 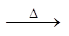 Al2O3 (s) + 2H2O(g)
Al2O3 (s) + 2H2O(g)
c) Organic matter, if present in the ore, gets expelled and the ore becomes porous. Volatile impurities are removed.
Roasting :
Generally used for sulphide ore.
Process : Concentrated ore is strongly heated in excess of air or O2 below its metling point.
(a) Roasting at moderate temperature :
2PbS + 3O2 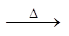 2PbO + 2SO2
2PbO + 2SO2
2ZnS + 2O2 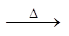 2ZnO + 2SO2
2ZnO + 2SO2
If temperature is low (500°C) & concentration of SO2 is high sulphate are produced.
PbS + 2O2 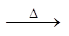 PbSO4
PbSO4
ZnS + 2O2 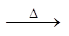 ZnSO4
ZnSO4
(b) Roasting at High temperature :
Self reduction / auto reduction / air reduction :
Sulphide ore of Cu, Pb, Hg & Sb when strongly heated in free supply of air, directly reduced to the metal this known as self reduction.
Cu2S (Copper glance) + O2 ¾® 2Cu + SO2
PbS (Gelena) + O2 ¾® Pb + SO2
HgS (Cinabar) + O2 ¾® Hg + SO2
Important Points
1.It remove impurities of As as As2O3, sulphur as SO2, P as P4O10 & Sb as Sb2O3
4M (M = As, Sb) + 3O2 ¾®2M2O3↑
S + O2 ¾®SO2↑
P4 + 4O2 ¾® P4O10↑
2. Impurities of CuS & FeS in SnO2 converted to CuSO4 & FeSO4
CuS + 2O2 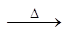 CuSO4
CuSO4
FeS + 2O2  FeSO4
FeSO4
Note : Calcination & Roasting carried out in a reverberatory furnace.
Smelting :
Slag formation : In many extraction processes, an oxide is added deliberately to combine with other impurities and form a stable molten phase immiscible with molten metal called a slag. The process is termed smelting.
The principle of slag formation is essentially the following :
Nonmetal oxide (acidic oxide) + Metal oxide (basic oxide) ¾® Fusible (easily melted) slag
Removal of unwanted basic and acidic oxides: For example, FeO is the impurity in extraction of Cu from copper pyrite.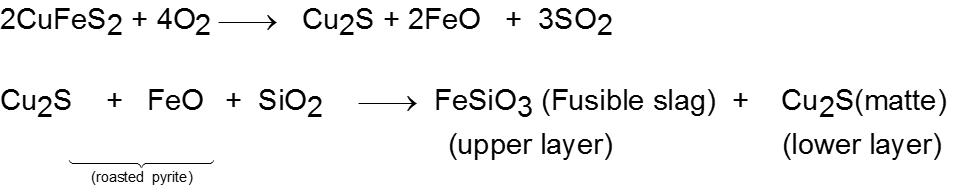
Matte also contains a very small amount of iron(II) sulphide.
To remove unwanted acidic impurities like sand and P4O10, smelting is done in the presence of limestone.
CaCO3 ¾® CaO + CO2
CaO + SiO2 ¾® CaSiO3 (fusible slag)
6CaO + P4O10 ¾® 2Ca3(PO4)2 (fusible slag - Thomas slag)
Properties of a slag :
(i) Slag is a fusible mass.
(ii) It has low melting point.
(iii) It is lighter than and immiscible with the molten metal. It is due to these impurities that the slag floats as a separate layer on the molten metal and can thus be easily separated from the metal. The layer of the slag on the molten metal prevents the metal from being oxidised.
Type of flux : Fluxes are of two types viz., acidic flux and basic flux.
(a) Acidic flux : It is an acidic oxide (oxide of a non-metal) like SiO2, P2O5, B2O3 (from borax). It is used to remove the basic impurity like CaO, FeO, MgO etc. The acidic flux combines with the basic impurity and forms a slag.
(b) Basic flux : It is a basic oxide (i.e., oxide of a metal) like CaO (obtained from lime stone, CaCO3), MgO (from magnesite, MgCO3), haematite (Fe2O3) etc. It is used to remove the acidic impurity like SiO2, P2O5 etc. The basic flux combines with the acidic impurity and forms a slag.
Thus, slag can be defined as a fusible mass, which is obtained when a flux reacts with an infusible acidic or basic impurity present in the oxide ore.
Reduction of a Metal Oxide
(1) Reduction with Carbon :
PbO + C ¾® Pb + CO
2Fe2O3 + 3C ¾® 4Fe + 3CO2
*** ZnO + C  Zn + CO (Extraction of Zn)
Zn + CO (Extraction of Zn)
*** SnO2 + 2C  Sn + 2CO
Sn + 2CO
(2) Reduction with CO :
Fe2O3 + 3CO ¾® 2Fe + 3CO2
Fe3O4 + 4CO ¾® 3Fe + 4CO2
Reduction with C & CO is carried out in blast furnace.
(3) Redution with Al :
GoldSchmidt or Aluminothermic process :
Metallic oxide of Cr & Mn reduced by Al & this reaction is known as thermite reaction.
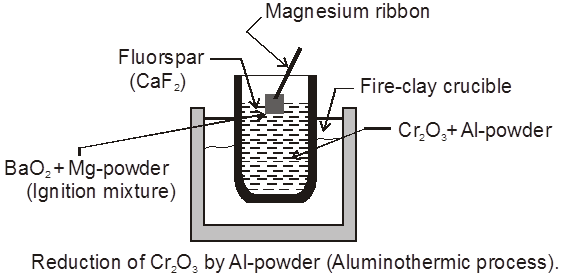
Mg + BaO2 ¾® BaO + MgO + Heat
(i) Cr2O3 + Al ¾®2Cr(l) + Al2O3
*** (ii) 3Mn3O4 + 8Al ¾® 4Al2O3 + 9Mn
(iii) 2Al + Fe2O3 ¾®Al2O3 + 2Fe
(iv) B2O3 + 2Al ¾® 2B + Al2O3
(4) Redution by Mg & Na :
(i) TiCl4 + 2Mg 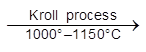 Ti + 2MgCl2
Ti + 2MgCl2
(ii) TiCl4 + 4Na 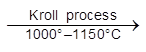 Ti + 4NaCl
Ti + 4NaCl
(5) Self reduction or auto reduction or air reduction :
Sulphide ore of some of the metal like Hg, Cu, Pb & Sb, when heated in air some part of these ore change into oxide or sulphate, thenthat part react with remaing part of sulphide ore to give its metal & sulphur dioxide.
This process is known as self reduction.
Ex. (i)(a) 2PbS + 3O2 ¾®2PbO + 2SO2
2PbO + PbS ¾®3Pb + SO2
(b) PbS + 2O2 ¾®PbSO4
PbSO4 + PbS ¾®2Pb + 2SO2
(ii) 2HgS + 3O2 ¾®2HgO + 2SO2
2HgO + HgS ¾®3Hg + SO2
(6) Electrolytic Reduction :
Electrolytic reduction is an expensive method than chemical method, that's why generally we do not use this method.
But when very high pure metal is required then we use this method.
This method is also used for highly reactive metal.
(i) Electrolyric reduction in aqueous solution :
This method is used when product does not react with water.
Electrolytic reduction of Cu & Zn from their sulphates.
(ii) In other solvents : Flourine react with water so it is produced by electrolysis of KHF2 dissolved in anhydrous HF.
(iii) In fused metal : When produced metal react with water, then metal is extracted from fused melt of their ionic salt.
Eg. (i) Al is extracted from electrolysis of fused mixture of Al2O3 and cryolite (Na3AlF6).
(ii) Extraction of Na by electrolysis of fused NaCl.
Note : In this electrolysis CaCl2 is added as impurity to lower the melting point from 800°C to 500°C.
(i) Hydro Metallurgy :
When metal can be extracted using solution without any heating or without any electrolysis then operation is known as hydrometallurgy.
Basic Step
(i) Dissolution of the valuable metal in aqueous solution.
(ii) Purification of leach solution.
(iii) Recovery of metal from purified solution.
Ex. Extraction of Ag & Au :
Metallic Ag dissolved in NaCN from ore of Ag & then precipitated with the help of Zn.
AgS(s) + 4CN¯ ¾® 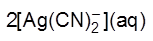 + S2–
+ S2–
2[Ag(CN)2]¯(aq) + Zn(s) ¾® [Zn(CN)4]2–(aq) + 2Ag(s)
(ii) Pyrometallurgy :
If furnace are used and ore are heated to extract metal then it is called pyrometallurgy.
Electrochemical principles of metallurgy :
Electrolytic reduction can be regarded as a technique for driving a reduction by coupling it through electrodes and external circuit to a reactive or a physical process with a more negative DG. The free energy available from the external source can be assessed from the potential it produces across the electrodes using the thermodynamic relation :
DG = –nFE ..........(i)
where n is the number of electrons transferred, F is Faraday’s constant (F = 96.5 kJ/mol) and Eº is electrode potential of the redox coupled formed in the system.
Hence, the total Gibb’s energy of the coupled internal and external process is
DG + DG (external) = DG – nFEext
If the potential difference of the external source exceeds
Eext = –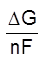
the reduction is thermodynamically feasible; thus, the overall process occurs with a decrease in free energy.
More reactive metals have large negative values of the electrode potential. So their reduction is difficult. If the difference of two E0 values corresponds to a positive E0 and consequently negative DG0 in equation (i), then the less reactive metal will come out of the solution and the more reactive metal will go to the solution, e.g.,
Cu2+ (aq) + Fe(s) —® Cu(s) + Fe2+(aq)
In simple electrolysis, the Mn+ ions are discharged at negative electrodes (cathodes )and deposited there. Precautions are taken considering the reactivity of the metal produced and suitable materials are used as electrodes. Sometimes a flux is added for making the molten mass more conducting.
Hydrometallurgy : The processing of ores and minerals as well as metals and their compounds at relatively low, often ambient temperatures employing aqueous solution is known as hydrometallurgy. Occasionally, organic reagents are also used. This method of extraction is generally used for low grade ores. Copper is extracted by hydrometallurgy from low grade ore it is leached out using acid and bacteria. The solution containing Cu2+ is treated with scrap iron or H2.
CuSO4 + Fe —® Cu(s) + FeSO4
A hydrometallurgical process for the extraction of metals from ores, concentrates, or secondary materials essentially contains three basic steps—dissolution of the valuable metal in the aqueous solution (leaching) purification of leach solution and subsequent recovery of metal from the purified solutions either by electrolysis or by adding some electropositive metal to it.
Some of the metals obtained by hydrometallurgy are as follows :
(A) Extraction of Ag and Au : Metals like Au and Ag can be precipitated for their salt solution by electropositive metals for example, Zn.
Metallic Ag is dissolved from its ore in dilute NaCN solution, and the solute so obtained is treated with scrap Zn when Ag is precipitated. Air is blown into the solution oxidize Na2S. Leaching the metals like silver, gold with CN– is an oxidation reaction (Ag ® Ag+ or Au ® Au+)
Ag2S (s) + 4CN– (aq) —® 2 [Ag(CN)2]– (aq) + S2– (aq)
2[Ag(CN)2]– (aq) + Zn (s) —® [Zn (CN)4]2– (aq) + 2Ag (s)
4Au (s) + 8 CN– (aq) + O2 (g) + 2H2O (l)—® 4 [Au(CN)2]– (aq) + 4OH– (aq)
2[Au(CN)2]– (aq) + Zn (s) —® [Zn(CN)4]2– (aq) + 2 Au (s)
Here Zn acts as reducing agent.
(B) Extraction of Aluminium : It involves the following processes
(a) Purification of bauxite :
(1) Leaching of Alumina from bauxite :
If Fe2O3 is main impurity (red bauxite) ® Bayer's/Hall's
If SiO2 is main impurity (white bauxite) ® Serpeck's process.
(i) Bayer's process :

(iii) Serpeck's process :
Used for white bauxite containg silica as impurities.
Al2O3 + N2 +  Coke AlN + CO↑
Coke AlN + CO↑
 Al(OH)3 + NH3 ↑
Al(OH)3 + NH3 ↑
 Al2O3 (pure)
Al2O3 (pure)
(2) Electrolytic reduction [Hall-Heroult process] :
Electrolysis of fused Al2O3 is difficult as its MP is very high (2323 K) & It is bed conductor of electricity in fused state.
So Al2O3 is mixed with Na3AlF6 or CaF2. Which lowers the MP (1173 K) & make alumina conducting.
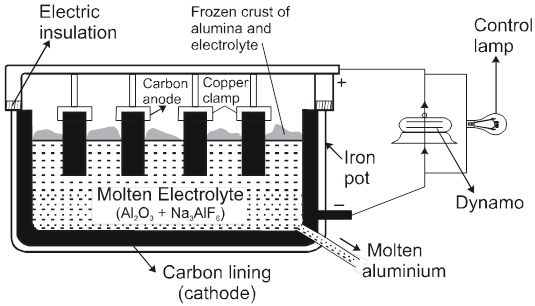
Cathode Þ Al3+ (Melt) + 3e– ® Al(l)
Anode Þ C(s) + O2– (Melt) ® CO(g) + 2e–
C(s) + 2O2– (Melt) ® CO2(g) + 4e–
Overall reaction Þ2Al2O3 + 3C ® 4Al + 3CO2
Note : During electrolytic reduction of aluminum, the carbon anodes are replaced from time to time because oxygen liberated at the carbon anodes react with anode to form CO & CO2.
Electrolytic refining of Al :
Hoop's process : For electrolytic refining of Al, Hoop's process is used.
Anode Þ Impure Al
Cathode Þ Pure Al
Electrolyte Þ Fused salt of Aluminium Fluoride
Note :The fused material remain in three different layer & remain separated because all the layer have different density.
Anode Þ Al(melt) ¾®Al3+ + 3e–
Cathode Þ Al3+ + 3e– ¾®Al
From anode (bottom layer), Al passes into solution as Al3+ ions and then from solution (middle layer) these Al3+ ion pass to cathode (top layer) and get reduced to pure metal.
Extraction of Na : The fused mixture of NaCl and CaCl2 is taken in Down’s cell which consists of circular iron cathode and carbon anode. On passing the electric current the following reactions take place :
Ionisation of NaCl : NaCl  Na+ + Cl–
Na+ + Cl–
Collection of Na at cathode : Na+ + e– ® Na(Reduction).
Collection of Cl2 at anode : Cl– + e– ®Cl (Oxidation), Cl + Cl ® Cl2 .
Na can also be obtained by electrolysing molten NaOH in Castner’s cell.
THERMODYNAMICS OF EXTRACTION : ELLINGHAM DIAGRAM OF A METAL
Ellingham Diagram
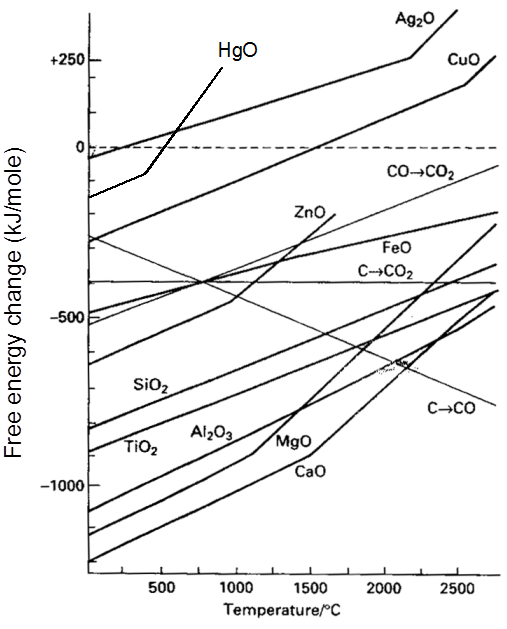
Thermodynamic of extraction :
For a Proces to be spontaneous DG must be negative.
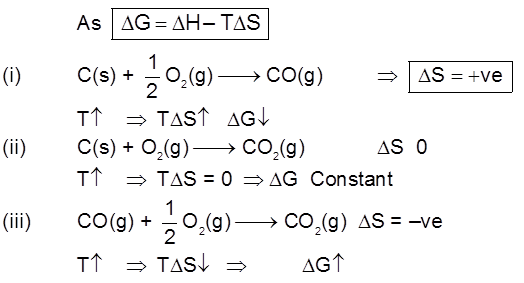
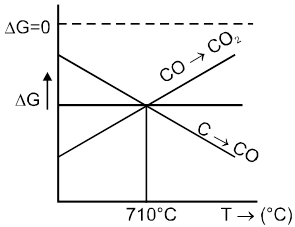
Ellingham Diagram of Metal
XM(s) + 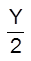 O2(g) ¾® MXOY(s)
O2(g) ¾® MXOY(s)
number of gaseous moles decreae with progress of reaction.
As DS = –ve If T Þ DG
Important Points
(1) Below 710°C, CO is better reducing agent than C.
(2) All the graphs are upgrowing and on increasing temperature, DG of formation of metal oxide become less negative, while on increasing temperature, DG of C ¾®CO reaction become more negative SO, C can reduce any metal from their metal oxide.
(3) Temperature above which DG of formation of metal oxide become positive, metal oxide become unstable & it decomposes into metal & oxygen.
(4) Theoritically, all metal oxide can be decomposed to give metal & oxygen, if suficiently high temperature is applied.
(5) When plot of one metal oxide is below the others then former metal is capable of reducing the later metal oxide into their metal.
Some important result
(1) All the three oxidation graph of carbon system are above the oxidation graph of ZnO upto temperature 1000°C. At this temperature C is thermodynamically capable of reducing ZnO to Zn. So C is better reducing agent for ZnO to Zn than CO.
(2) Below 1500°C temperature, the graph of MgO lies below the graph of Al2O3, so below this temperature Al cannot reduce MgO, but above this temperature graph of Al2O3 shifts below the graph of MgO so above 1500°C, Al can reduce MgO.
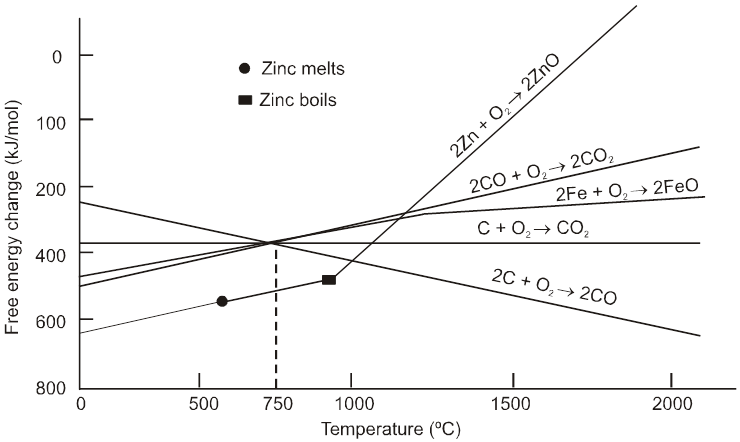

 ACME SMART PUBLICATION
ACME SMART PUBLICATION
