Motion in a plane
Motion is a plane (2-D) that will be difficult to understand if we would treat it like a 2-D motion. For simplicity, we can break the motion of 2-D into two independent motions along with X and Y directions ( two 1-D motions) with which we are already familiar.
We use the equation of motion in 1-D with subscripts x and y for motion along the X and Y direction.

We resolve the force in the X and Y direction and call it Fx and Fy.
Then from the force components, we find acceleration along the x and y-direction.
ax=Fx/m ; and ay= Fy/m
a= ax i + ay j
Then similarly we can resolve the initial velocity ‘u’ along the x and y direction as ux and uy.
Initial speed u= ux i + uy j
Then we can use the equation of motion separately for x and y directions and find the final velocity and displacement along x and y (vx , vy ,x,y).
final speed v= vx i + vy j
displacement r= x i + y j
Projectile Motion
Motion of an object under gravity is called projectile motion.
Projectile motion are of three types: Oblique projectile, horizontal projectile and projectile motion along an inclined plane.
In this discussion, we will discuss oblique and horizontal projectiles.
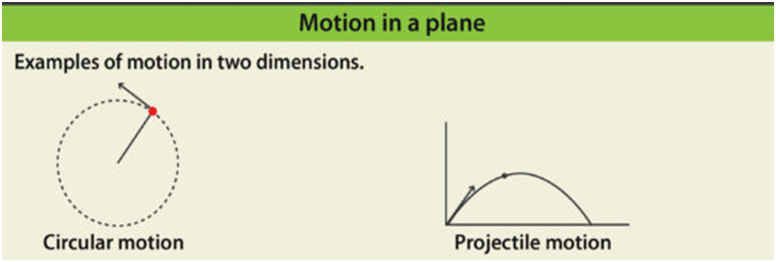
Figure given below is an example of a horizontal projectile. Here an object is thrown with velocity ‘u’ in the horizontal direction from a height of H and the object follows a projectile path.
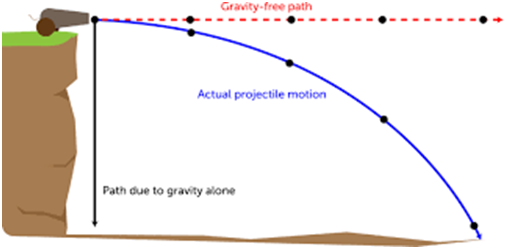
Figure given below is the example of the oblique projectile in which an object is thrown from a ground with velocity u making some angle Ө with the horizontal.
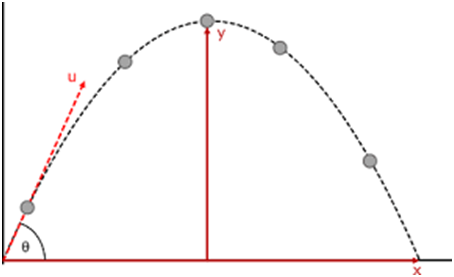
Oblique projectile
In this type of projectile, an object is thrown with the initial velocity ‘u’ which makes an angle θ with the horizontal direction. The only force here is gravity which acts in ‘y direction’. There is no force along the x-axis.
Fx=0 , Fy=mg
Also ax=0 , ay=g (downward)
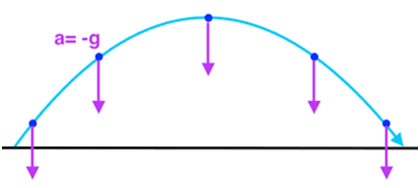
We will discuss and calculate Horizontal distance, maximum height and time of flight T. As you can see from the projectile path shown below that the motion is symmetric about maximum height.
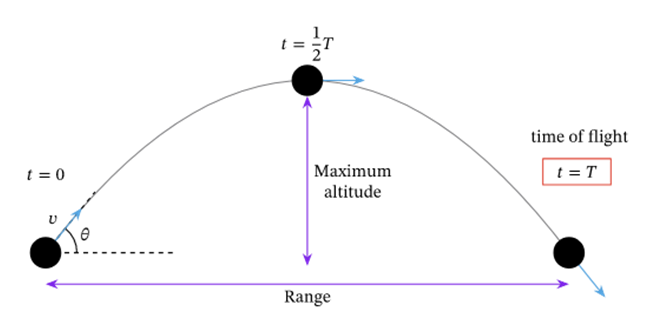
To calculate maximum height and time of flight we will use the ‘y - direction’ motion. And to calculate the range we will use the equation of x-motion.
Since there is a force along only the y-direction hence acceleration to velocity along with the y-axis changes while velocity along y remains the same as no force is acting on x.
Components of initial velocity ‘u’ : ux= u cos θ , uy= u sin θ
Acceleration ax=0 , ay=g (downward)
We know that at maximum height velocity along y will be zero.
Vy=0 at t=T/2 where T= time of flight. Using this we have,
v_(y_ )=u_y+a_y t ; 0=u sinθ -g(T/2) ; u sinθ= g(T/2)
Therefore we have the time of flight T= 2 u sinθ/g
Now we will find maximum height using the 2nd equation of motion, here we will consider the first half of motion. (t=T/2) and y= ymax =H
〖v_y〗^2= u_y+2a_y y ,
0= u^2 sin^2 θ-2gH ; 2gH= u^2 sin^2 θ .
Therefore we have a maximum height of H=u^2 sin^2 θ/(2g)
To calculate the range we need to use x motion. Motion of X direction is uniform motion as ax=0 so , x= U_x*Time of flight
R= u cosθ* (2 u sinθ/g)=u^2 (2 sinθ cosθ)/g= u^2 sin 2θ/g
Therefore we have Range R= u^2 sin 2θ/g
Equation of path of projectile motion.
Let initial position is (x0 ,y0) then y (t) , y as a function of time will be given as
y(t)= y_0+u_y t+ 1/2 gt^2 ; u_y= u sinθ , t=((x-xo))/(u cosθ)
When (x0 , yo)= (0,0) when object starts from origin
Then equation of path of projectile motion will be given as
y=x tanθ-(g x^2)/(2 u^2 cos^2 θ)
This is an equation of a parabola and hence we get a parabolic path for an object moving in a plane under gravity.
Discussion over oblique projectiles.
- Range of the projectile is maximum for θ=45.
R=u^2 sin2θ/g R is max when sin 2θ=1; 2θ=90; θ=45
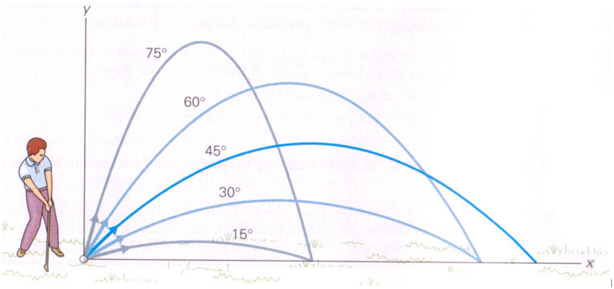
- Projectile for different initial speeds for a given angle.
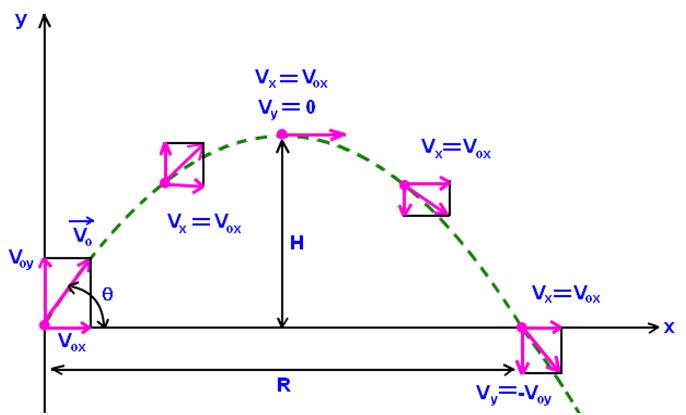
- The velocity with which the object strikes the ground is same as with it was thrown.
Horizontal projectile
In a horizontal projectile, an object is thrown from a height ‘ h’ with a horizontal velocity ‘vo’. Here the only force acting on the object is gravity.
There is no force acting in the horizontal direction. This is exactly like an oblique case.
Fx=0 , Fy=mg
Also ax=0 , ay=g (downward)
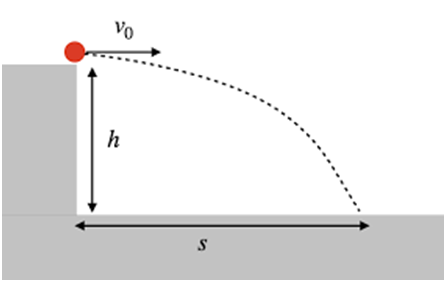
We can find the time of flight ‘T’, horizontal distance ‘s’ and final velocity ‘v’ by using the equation of motion in x and y directions.
To find the time of flight we will use the equation of motion in the y-direction
Here Y=h, uy=0 as initially there was only horizontal velocity ‘vo’
y=u_y t+1/2 gt^2 ; h= 0+ 1/2 gt^(2 ) ; t^2=2h/g ; t=√(2h/g)
Therefore the time of flight T=√(2h/g)
Now to find the horizontal distance traveled we will use motion along the x-direction. As motion along the x-direction is uniform motion
So X distance= speed in x-direction* time of flight
s= vo √(2h/g)
Therefore horizontal distance traveled is s= vo √(2h/g)
To find the final velocity of the object we need to use both motions along x and y-direction. We will find the final velocity along the x and y direction and then find its magnitude.
v_y=u_y+ a_y t ; v_y=0 +gt=g √(2h/g)
Thus final velocity along y v_y=√2gh
Final velocity along x v_x=vo, as there is no change in velocity along the x-direction.
The magnitude of final velocity v=√(vx^2+ vy^2 )= √( vo^2+2gh)
As you can see in the illustration given below the horizontal remains the same but the vertical velocity was initially zero but keeps on increasing as the object is falling.
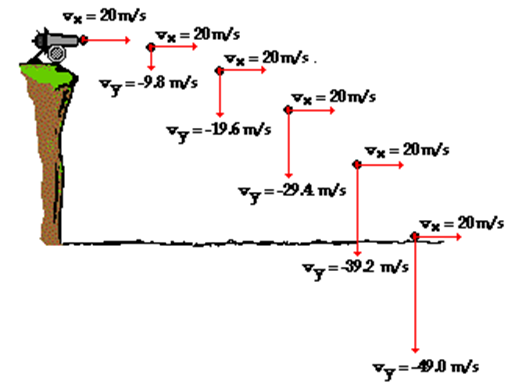
Example of horizontal projectile
Consider a horizontal projectile with an initial speed vo= 10 m/s. It is given that it takes 5 seconds to reach the ground level. We have to find the height, final vertical velocity and the horizontal distance traveled.

Uniform circular motion
Motion of an object in a circular path with uniform speed is called uniform circular motion.
In a uniform circular motion, the speed of the object remains the same but the velocity changes throughout the motion as the direction of velocity changes. As you can see from the picture given below that velocity is always tangent to the path and its direction changes continuously.
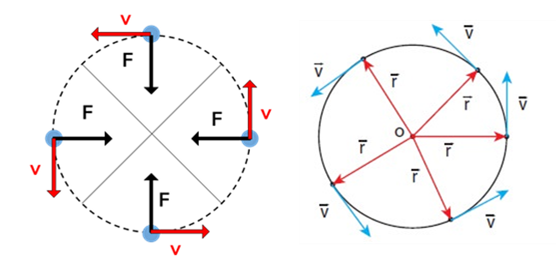
Force needed to keep the object moving in the circular path is called centripetal force which is always directed towards the center. So there is an acceleration acting on the particle which is toward the center and called centripetal acceleration.
We have centripetal force Fc= -m v^2/r and hence centripetal acceleration a_c= 〖-v〗^2/r, where r is the radius of the circle.
Time period of uniform circular motion T= circumference/ velocity
T=2Πr/v, this would be the time taken by the particle in one complete revolution.
Frequency of the uniform circular motion f=v/2Πr
Angular frequency ‘w’ is the rate of change of angular displacement θ
w=Δθ/Δt
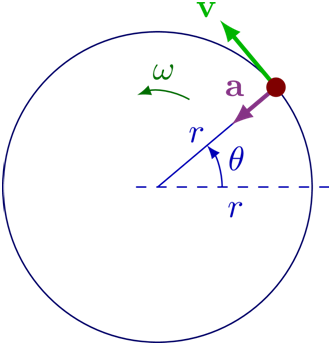
If the distance traveled in Δt is Δs then the velocity will be given as
v=(Δs )/Δt ; here s=rθ ; v=r Δθ/Δt=r w ; v=rw
We can express fc, ac, T, and f in terms of w
centripetal force fc=-m v^2/r=-mw^2 r
centripetal acceleration ac= 〖-w〗^2 r
Time period T= 2Π/w
frequency f= w/2Π

 Madhava Publications
Madhava Publications
