3. Moment of Inertia

Moment of Inertia

The moment of inertia of an object is a calculated measure for a rigid body that is undergoing rotational motion around a fixed axis: that is to say, it measures how difficult it would be to change an object's current rotational speed. That measurement is calculated based upon the distribution of mass within the object and the position of the axis, meaning that the same object can have very different moments of inertia values depending upon the location and orientation of the axis of rotation.

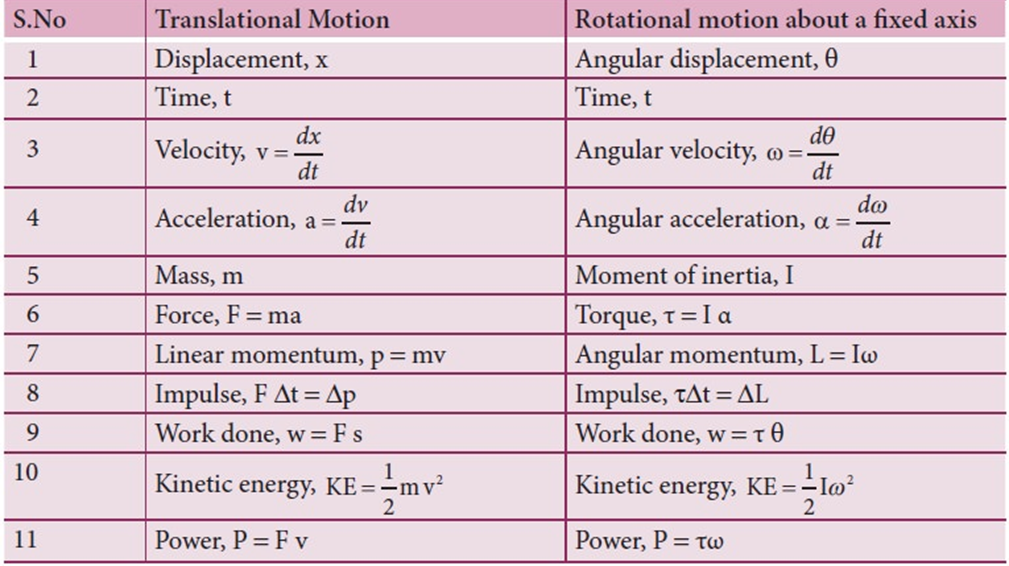
Moment of Inertia in rotational motion is analogous to mass in translational motion.

The moment of inertia of an object rotating around a fixed object is useful in calculating two key quantities in rotational motion:

Rotational kinetic energy:

Angular Momentum: L = Iω

You may notice that the above equations are extremely similar to the formulas for linear kinetic energy and momentum, with a moment of inertia "I" taking the place of mass "m" and angular velocity "ω" taking the place of velocity "v," which again demonstrates the similarities between the various concepts in rotational motion and in the more traditional linear motion cases.

The International System of Units (SI unit) of the moment of inertia is one kilogram per meter squared (kg-m2).

Calculation of Moment of Inertia

To calculate the moment of inertia in its most general form. It basically consists of the following steps:

1. Measure the distance r from any particle in the object to the axis of symmetry.
2. Square that distance.
3. Multiply that squared distance times the mass of the particle.
4. Repeat for every particle in the object.
5. Add all of these values up.

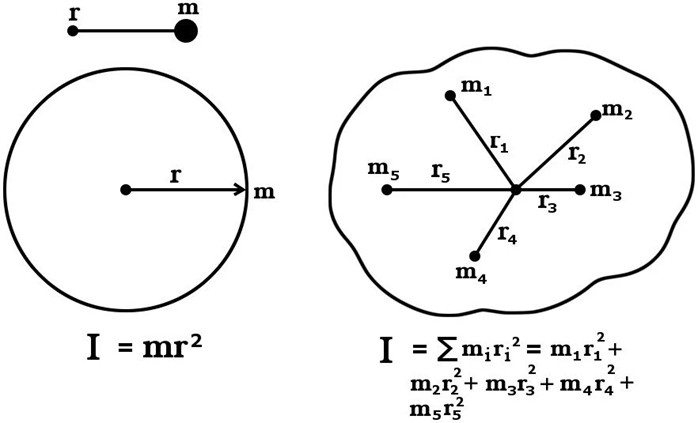
Moment of Inertia is denoted by ‘I’ = ∑_(i=1)^n   m_(i ) 〖r_i〗^2

Radius of gyration

The radius of gyration of anybody about the axis of rotation is defined as that radial distance from the axis of rotation, at which the entire mass of that body is concentrated. Thus, the point will have a moment of inertia at this particular point also.  It is denoted by k.

This is also referred to as the measure of the way in which the mass of a rotating rigid body can be distributed about its axis of rotation.

If the moment of Inertia is represented by me, then its value is  I= MK2 if a body has n particles, each of them has mass m.

Let   r₁,  r₂, r₃, r₄, ........r_n be the perpendicular distance of the object from the rotation axis.

Then, MOI or the moment of inertia of the body on its rotational axis is calculated as

I= m₁ r1² + m2 r2² +m3r3² +...............+ mn^rn²

If the mass of all the particles is the same as m, then the equation can be written as:

Moment of Inertia  I= mr1²+ mr2²+ mr3²+ .... m rn ²

It can also be written as  I = m ( r1² +r2²+ r3³ + ........+rn²)

If we multiply and divide the equation by n, then the equation will be,

I= m n ( r1² +r2²+ r3³ + ........+rn²)/n

We have total mass M= m n so,

I= M( r1² +r2²+ r3³ + ........+rn²)/n = Mk ²

Therefore we have   k² = ( r1² +r2²+ r3³ + ........+rn²)/n

So, radius of gyration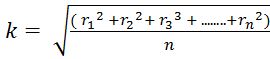  

This clearly shows that k is the radius of gyration of a body about an axis is the root of the mean square distance of several different body particles from the rotational axis.

Theorems of perpendicular and parallel axis

There are two useful theorems relating to the moment of Inertia. By applying these theorems it is easier to find out the moment of inertia of some regular-shaped bodies.

Parallel Axis theorem - The Parallel axis theorem states that the moment of inertia of a body (rigid body) about an axis is equal to its moment of inertia about an axis passing through the center of mass of the body parallel to the given axis plus the product of the mass of the body and the square of the perpendicular distance between the two axes parallel to each other.

I =  I G + Md²

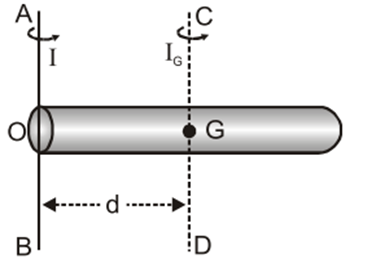
Where I = moment of inertia about axis AB and I_G = moment of inertia about the center of the mass CD, M= total mass of rod and, d = distance between axis AB and CD

Perpendicular Axis theorem

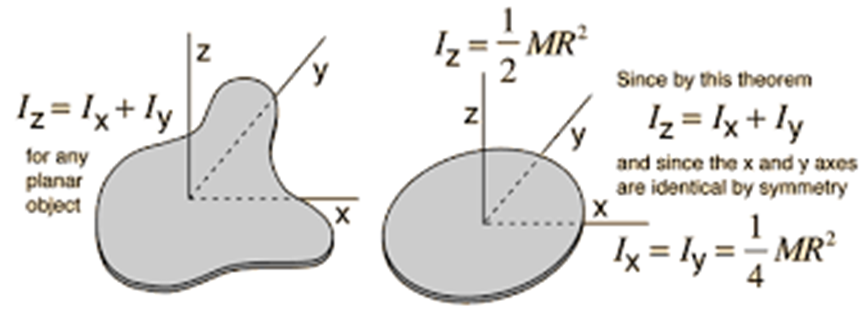
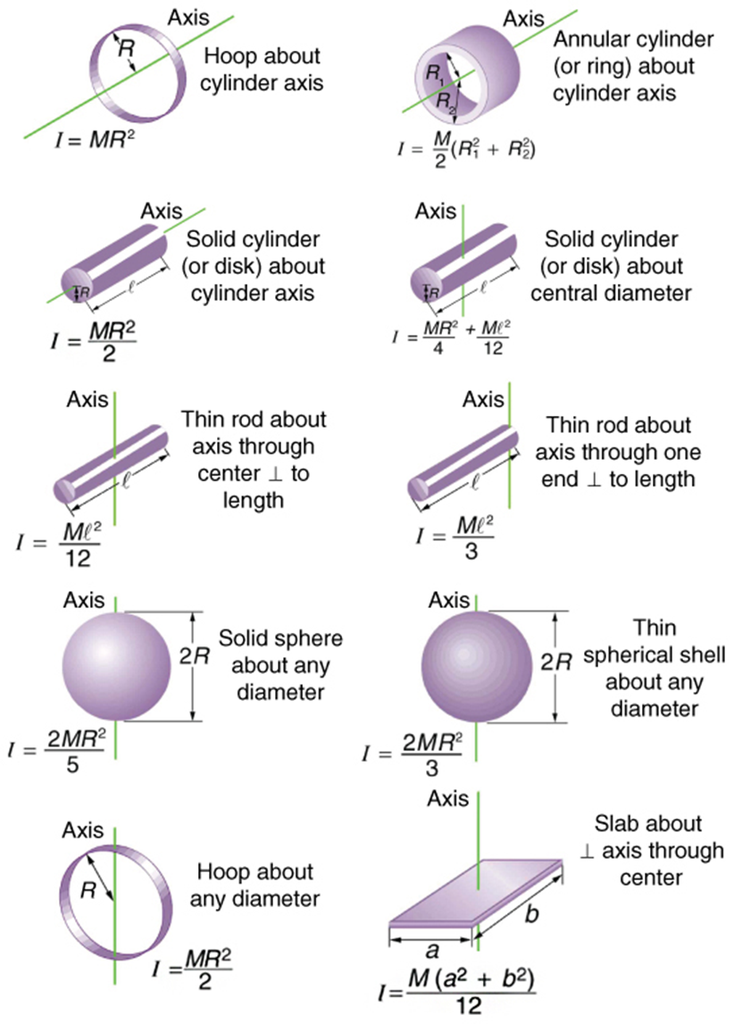
Moment of Inertia of various geometric shapes about the different axis of rotation

Comparison between translational and rotational motion