- Books Name
- AMARENDRA PATTANAYAK Mathmatics Book
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 11
- Subject
- Mathmatics
General Equation of a Line
General equation of a line is Ax + By + C = 0. The inclination of angle θ to a line with a positive direction of X-axis in the anti-clockwise direction, the tangent of angle θ is said to be slope or gradient of the line and is denoted by m
General equation of first degree in two variables,
Ax + By + C = 0, where A, B and C are real constants such that A and B are not zero
simultaneously. Graph of the equation Ax + By + C = 0 is always a straight line.
Therefore, any equation of the form Ax + By + C = 0, where A and B are not zero
simultaneously is called general linear equation or general equation of a line.
Different forms of Ax + By + C = 0 The general equation of a line can be
reduced into various forms of the equation of a line.
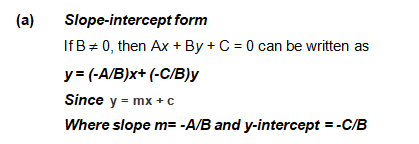
If B = 0, then x = - C/A which is a vertical line whose slope is undefined and x-intercept is -C/A.
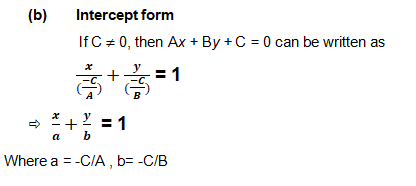
If C = 0, then Ax + By + C = 0 can be written as Ax + By = 0, which is a line passing through the origin and, therefore, has zero intercepts on the axes.


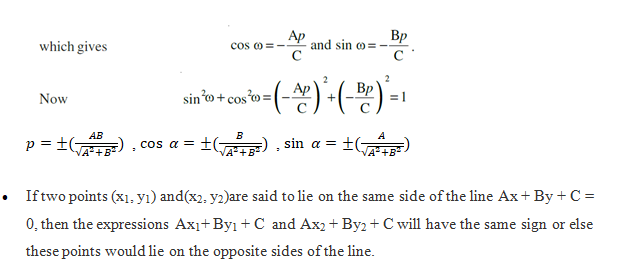
(Q1) The equation of a line is given by, 2x – 6y +3 = 0. Find the slope and both the intercepts.
Solution:
The given equation 2x – 6y + 3 = 0 can be represented in slope-intercept form as:
y = x/3 + 1/2
Comparing it with y = mx + c,
Slope of the line, m = 1/3
Also, the above equation can be re-framed in intercept form as;
x/a + y/b = 1
2x – 6y = -3
x/(-3/2) – y/(-1/2) = 1
Thus, x-intercept is given as a = -3/2 and y-intercept as b = 1/2.
(Q2) The equation of a line is given by, 13x – y + 12 = 0. Find the slope and both the intercepts.
Solution: The given equation 13x – y + 12 = 0 can be represented in slope-intercept form as:
y = 13x + 12
Comparing it with y = mx + c,
Slope of the line, m = 13
Also, the above equation can be re-framed in intercept form as;
x/a + y/b = 1
13x – y = -12
x/(-12/13) + y/12 = 0
Thus, x-intercept is given as a = -12/13 and y-intercept as b = 12.
Example: Show that two lines a1x + b1 y + c1 = 0 and a2x + b2 y + c2 = 0, where b1,b2 ¹ 0 are:

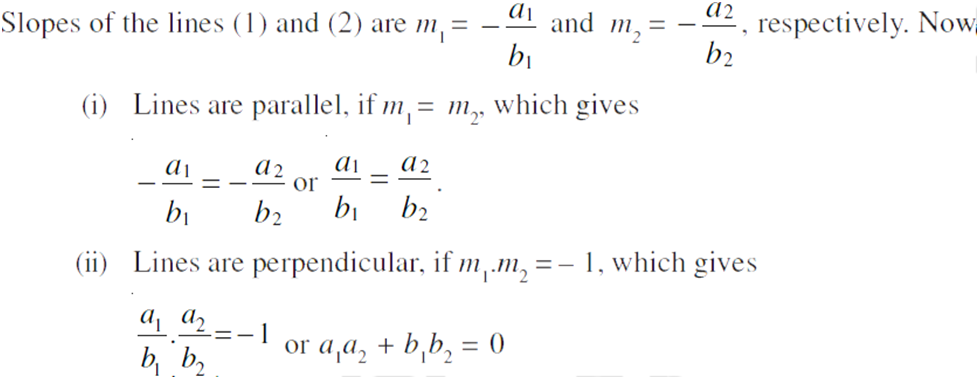

 KRISHNA PUBLICATIONS
KRISHNA PUBLICATIONS
