1. Intuitive idea of limits and Derivatives
- Books Name
- AMARENDRA PATTANAYAK Mathmatics Book
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 11
- Subject
- Mathmatics
Chapter 13
Limits and Derivatives
Intuitive idea of limits and Derivatives:
The concept of the limit of a function is essential to the study of calculus. It is used in defining some of the most important concepts in calculus—continuity, the derivative of a function, and the definite integral of a function.
A limit tells us the value that a function approaches as that function's inputs get closer and closer to some number. The idea of a limit is the basis of all calculus.
The limit of a function f( x) describes the behavior of the function close to a particular x value. It does not necessarily give the value of the function at x. You write , which means that as x “approaches” c, the function f( x) “approaches” the real number L
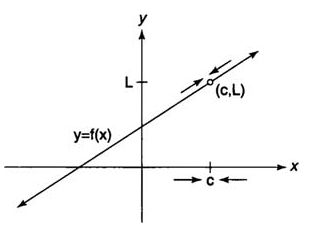
Fig. The limit of f(x) as x approaches c.
In other words, as the independent variable x gets closer and closer to c, the function value f( x) gets closer to L. Note that this does not imply that f( c) = L; in fact, the function may not even exist at c (Figure 2) or may equal some value different than L at c .
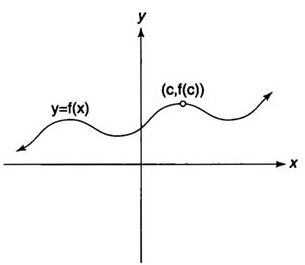
f ( c) does not exist, but ![]()
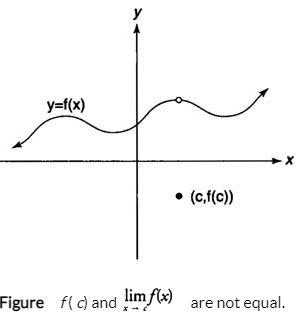
If the function does not approach a real number L as x approaches c, the limit does not exist; therefore, you write ![]() Does Not Exist. Many different situations could occur in determining that the limit of a function does not exist as x approaches some value.
Does Not Exist. Many different situations could occur in determining that the limit of a function does not exist as x approaches some value.
2. Limits ,Types Of limits ,Existence of limits and Algebra of limits
- Books Name
- AMARENDRA PATTANAYAK Mathmatics Book
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 11
- Subject
- Mathmatics
Limits, Types Of limits, Existence of limits and Algebra of limits
Definition of a Limit (an informal view)
The intuitive definition for ![]() =L is the value of f(x) can be made arbitrarily close to L by making x sufficiently close, but not equal to, a .
=L is the value of f(x) can be made arbitrarily close to L by making x sufficiently close, but not equal to, a .
The (ε, δ)-definition of limit : For every real ε > 0, there exists a real δ > 0 such that for all real x, 0 < | x − a | < δ implies | f(x) − L | < ε.
As it is the formal definition of limit, I think it should be precise but somewhat should include the mean of the above intuitive definition, so as for "f(x) can be made arbitrarily close to L" in the intuitive definition correspond to “For every real ε > 0,| f(x) − L | < ε” in the formal definition, it's fine! but does “making x sufficiently close, but not equal to, a .” correspond to “there exists a real δ > 0 such that for all real x, 0 < | x − a | < δ” ? This is the point I cannot understand, because I am not sure if “there exists a real δ > 0 such that for all real x, 0 < | x − a | < δ” shows "x close enough, but not equal, to a".
Example:
limx→2 x2
and
|f(x)−4|=|x2−4|=|x−2||x+2|.
The first thing you should notice is we have a |x+2| term that us unwanted, so we need to bound it under ϵ.
Because we have 0<|x−2|<δ, this term will take itself out if δ<1.
Choosing δ<1, we have |x+2|<δ+4<δ+4δ=5δ because |x−2|<δ,
so we can choose δ<min(1,ϵ/5) then,
|f(x)−4|=|x−2||x+2|<|x+2|<5δ≤5ϵ/5=ϵ.
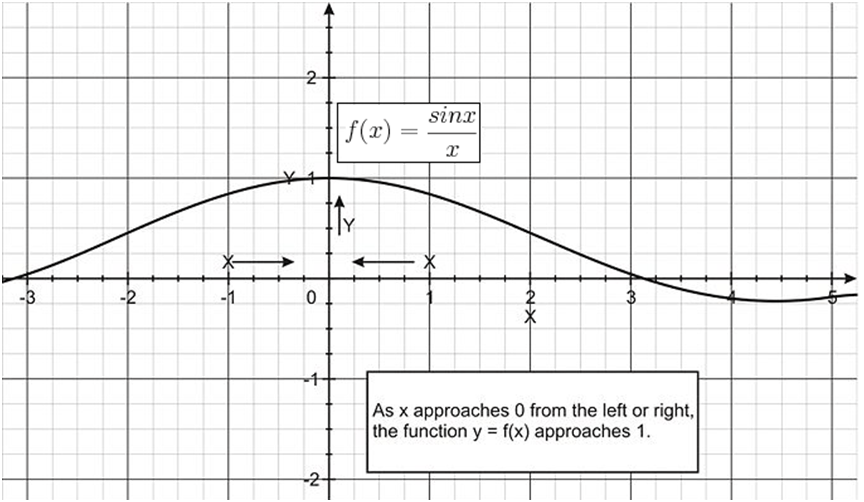
Example 2: Make a conjecture about the value of the limit ![]() where x is in radians.
where x is in radians.
Solution: The function here is not defined at x = 0. With the help of a computing utility, we can obtain the table below.

The data in the table suggest thats ![]() The graph below supports this hypothesis.
The graph below supports this hypothesis.
Example:
Make a conjecture about the value of the limit of ![]()
Solution: Notice that the function ![]() is not defined at x = 0. The table below shows samples of x-values approaching 0 from the left side and from the right side. In both cases, the values of f(x), calculated to at least 5 decimal places, get closer and closer to 6. Thus our conjecture is that
is not defined at x = 0. The table below shows samples of x-values approaching 0 from the left side and from the right side. In both cases, the values of f(x), calculated to at least 5 decimal places, get closer and closer to 6. Thus our conjecture is that ![]()

Another way of seeing this is to graph f(x) (shown below). Notice that the x-values approach 0 from the left side and from the right side. In both cases, the values of f(x) appear to get closer and closer to 6.
Hence, again our conjecture is that ![]()

Example: Consider the function f(x) = x + 10. We want to find the limit of this function at x = 5. Let us compute the value of the function f(x) for x very near to 5.

we deduce that value of f(x) at x = 5 should be greater than 14.995 and less than 15.001 assuming nothing dramatic happens between x = 4.995 and 5.001. It is reasonable to assume that the value of the f(x) at x = 5 as dictated by the numbers to the left of 5 is 15,
i.e.,
![]()
Similarly, when x approaches 5 from the right, f(x) should be taking value 15,
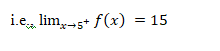
Hence, it is likely that the left hand limit of f(x) and the right hand limit of f(x) are
both equal to 15. Thus,
![]()
This conclusion about the limit being equal to 15 .
Example:

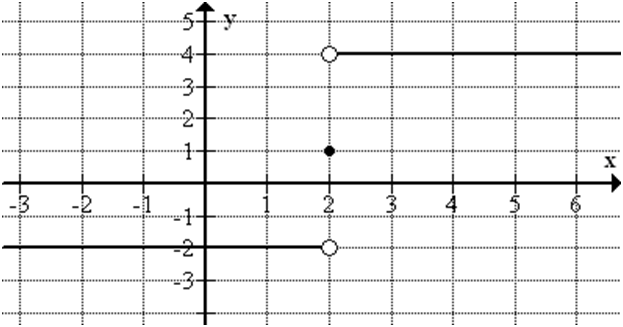

Types of Limits:
Besides ordinary, two-sided limits, there are one-sided limits (left- hand limits and right-hand limits), infinite limits and limits at infinity.
One-Sided Limits :
A left-hand limit means the limit of a function as it approaches from the left-hand side. On the other hand, A right-hand limit means the limit of a function as it approaches from the right-hand side.

Example:
Let us Consider ![]() .
.
One might think that since ![]() as x → 5, it would follow that
as x → 5, it would follow that ![]() .
.
But since ![]() = (x − 5)(x + 1) < 0 when x is close to 5 but smaller than 5,
= (x − 5)(x + 1) < 0 when x is close to 5 but smaller than 5,![]() is undefined for some values of x very close to 5 and the limit as x → 5 doesn’t exist.
is undefined for some values of x very close to 5 and the limit as x → 5 doesn’t exist.
But we would still like a way of saying ![]() is close to 0 when x is close to 5 and x > 5, so we say the Right-Hand Limit exists, write
is close to 0 when x is close to 5 and x > 5, so we say the Right-Hand Limit exists, write ![]() = 0 and say
= 0 and say ![]() approaches 0 as x approaches 5 from the right.
approaches 0 as x approaches 5 from the right.
Similar, we would still like a way of saying ![]() is close to 0 when x is close to 5 and x < 5, so we say the Left-Hand Limit exists, write
is close to 0 when x is close to 5 and x < 5, so we say the Left-Hand Limit exists, write ![]() = 0 and say
= 0 and say ![]() approaches 0 as x approaches 5 from the left
approaches 0 as x approaches 5 from the left
Sometimes we have a Left-Hand Limit but not a Right-Hand Limit. Sometimes we have both Left-Hand and Right-Hand Limits and they’re not the same. Sometimes we have both Left-Hand and Right-Hand Limits and they’re equal, in which case the ordinary limit exists and is the same.
Example:

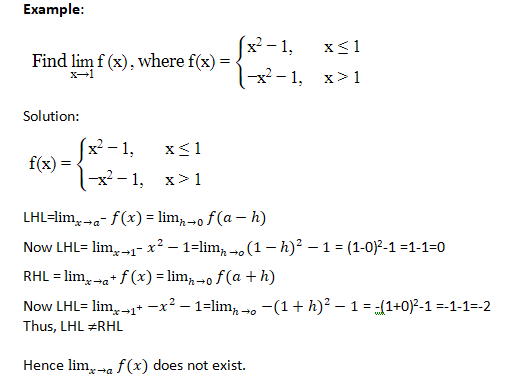
Limits at Infinity:


Calculating Limit at infinity

Example:
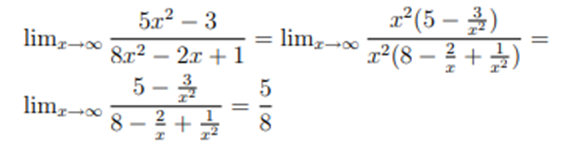


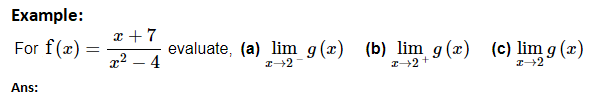
Let’s start off by acknowledging that for x→2− we know x<2.
For the numerator we can see that, in the limit, we will get 9.
Now let’s take care of the denominator. First, we know that if we square a number less than 2 (and greater than -2, which it is safe to assume we have here because we’re doing the limit) we will get a number that is less than 4 and so, in the limit, we will have,
x2−4→0−
So, in the limit, the numerator is approaching a positive number and the denominator is an increasingly small negative number. The quotient must then be an increasing large negative number or,
![]()
Note: that this also means that there is a vertical asymptote at x=2.
(b)
Let’s start off by acknowledging that for x→2+ we know x>2.
For the numerator we can see that, in the limit, we will get 9.
Now let’s take care of the denominator. First, we know that if we square a number greater than 2 we will get a number that is greater than 4 and so, in the limit, we will have,
x2−4→0+
So, in the limit, the numerator is approaching a positive number and the denominator is an increasingly small positive number. The quotient must then be an increasing large positive number or,
Note: that this also means that there is a vertical asymptote at x=2, which we already knew from the first part.
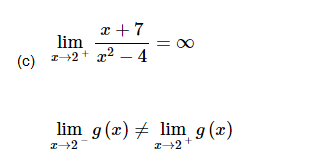
and so, from our basic limit properties we can see that ![]() does not exist.
does not exist.
For the sake of completeness and to verify the answers for this problem here is a quick sketch of the function.
Determinate limits:

Indeterminate limits:
Suppose we have to calculate a limit of f(x) at x→a. Then we first check whether it is an indeterminate form or not by directly putting the value of x=a in the given function. If we get ![]() = 0/0, ∞/∞, 0 . ∞/∞, 1∞, ∞-∞ , ∞∞ , 0∞, 00 these all are called indeterminate forms. L’Hospital’s Rule is applicable in the first two cases, ie 0/0 and ∞/∞.
= 0/0, ∞/∞, 0 . ∞/∞, 1∞, ∞-∞ , ∞∞ , 0∞, 00 these all are called indeterminate forms. L’Hospital’s Rule is applicable in the first two cases, ie 0/0 and ∞/∞.
For solving these limit , we have to follow the different methods like
- Factorization
- Rationalization
- Expansion
- Logarithm use
- L’Hospital Rule

Example: Find the limit of limx→2 [x3 + 2x2 + 4x – 2].
Answer :
limx→2 [x3 + 2x2 + 4x – 2] = limx→2 x3 + 2 limx→2 x2 + 4 limx→2 x – limx→2 2
= 23 + 2×22 + 4×2 − 2 = 22.
Example : Find the limit of limx→0 (sin 4x/tan x).
Answer :
limx→0 (sin 4x / tan x) = limx→0 [(sin 4x / 4x) × (4x / tan x)] (multiplying and dividing by 4x)
or, limx→0 (sin 4x / tan x) = limx→0 (sin 4x / 4x) × 4 limx→0 (x / tan x )
= 1 × 4 = 4 (by using L-Hospital’s Rule).
Algebra of limits:

3. Limits of polynomial, rational, trigonometric, exponential and logarithmic functions
- Books Name
- AMARENDRA PATTANAYAK Mathmatics Book
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 11
- Subject
- Mathmatics
Limits of polynomial, rational, trigonometric, exponential and logarithmic functions
Limits of polynomials and rational functions- A function f is said to be a polynomial function of degree n f(x) = a0 + a1x + a2x2 +. . . + anxn, where ai ‘s are real numbers such that an ¹ 0 for some natural number n.

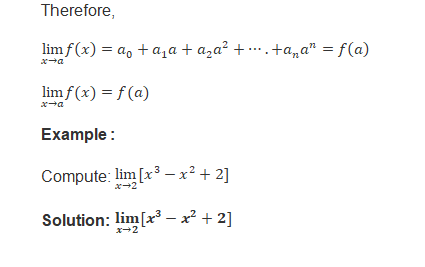
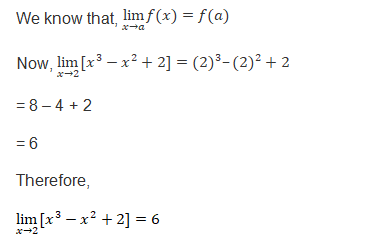
Limits of Rational Functions:
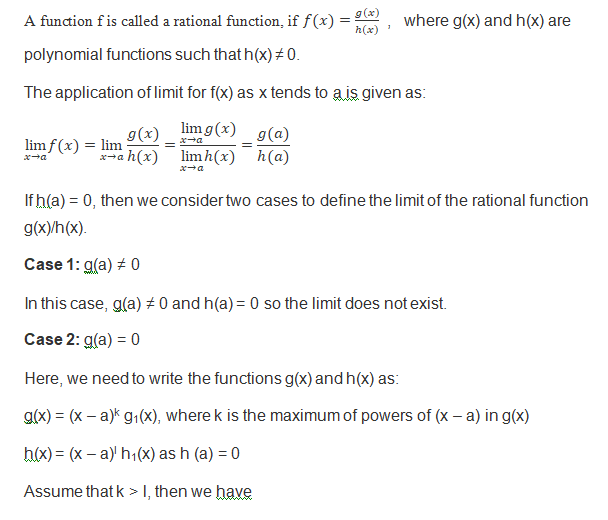

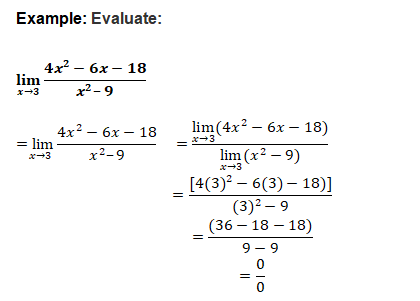
By evaluating the function at 2, we got 0/0.
So, let us factorise the functions to cancel the factors if possible.
4x2 – 6x – 18 = 4x2 – 12x + 6x – 18
= 4x(x – 3) + 6(x – 3)
= (x – 3)(4x + 6)
And x2 – 9 = x2 – 32 = (x – 3)(x + 3)
Thus,
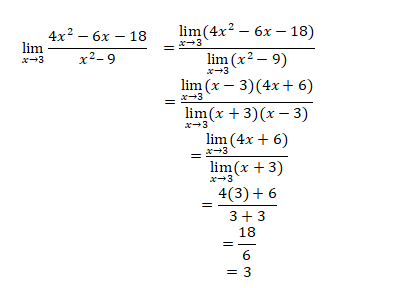

Limits of Trigonometric Functions:
Theorem: Let f and g be two real valued functions with the same domain such that
f (x) £ g( x) for all x in the domain of definition, For some a, if both limx®a f(x) and limx®a g(x) exist, then limx®a f(x) £ limx®a g(x).
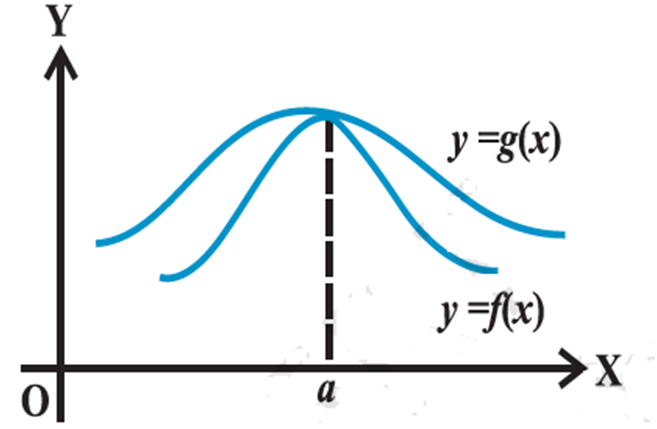
Sandwich Theorem/Squeeze Principle :
If f, g and h are three functions such that f(x) < g(x) < h(x) for all x in some interval containing the point x = a, and If
![]()
Some standards limits formulae are:
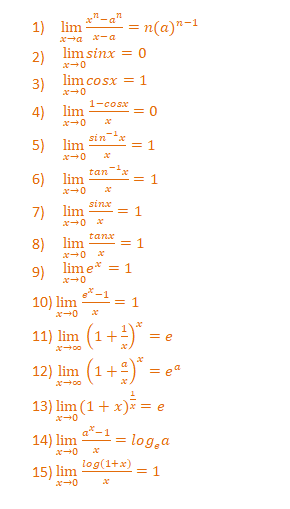
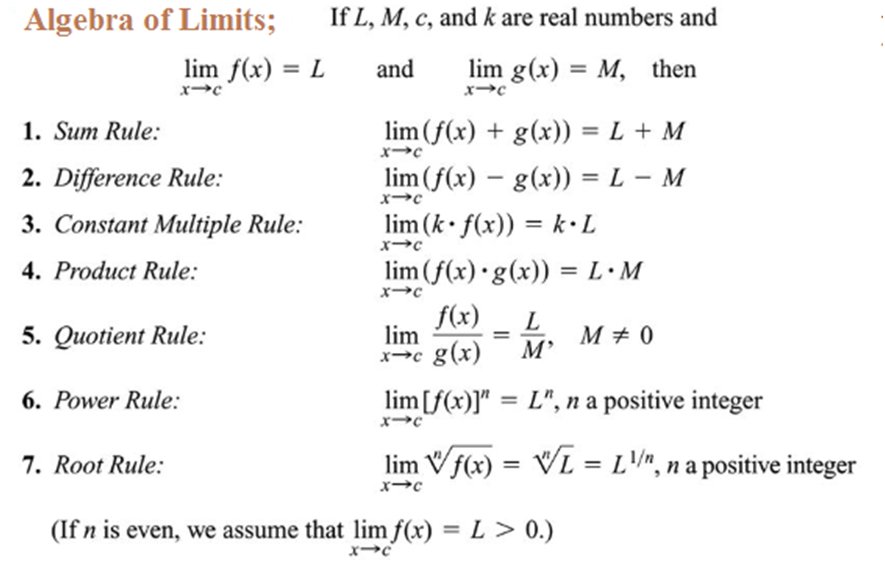
Limits of polynomials and rational functions: A function f is said to be a polynomial function of degree n f(x) = a0 + a1x + a2x2 +. . . + anxn, where ais are real numbers such that an ¹ 0 for some natural number n.
We know that limx->a x = a. Hence
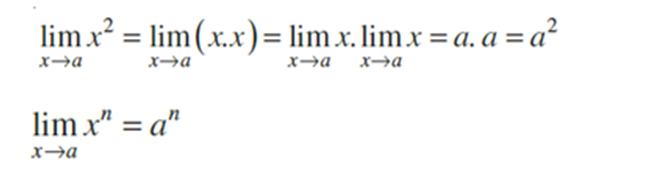
4. Derivatives ,Existence of Derivative and Algebra of Derivatives
- Books Name
- AMARENDRA PATTANAYAK Mathmatics Book
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 11
- Subject
- Mathmatics
Derivatives, Existence of Derivative and Algebra of Derivatives
Definition: Suppose f is a real valued function and a is a point in its domain of definition. The derivative of f at a is defined by
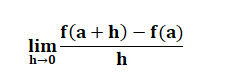
provided this limit exists. Derivative of f (x) at a is denoted by f’(a). Observe that f’(a) quantifies the change in f(x) at a with respect to x.
It is called first principle method or abinitio method or definition method.
Derivatives are defined as the varying rate of change of a function with respect to an independent variable. The derivative is primarily used when there is some varying quantity, and the rate of change is not constant. The derivative is used to measure the sensitivity of one variable (dependent variable) with respect to another variable (independent variable).
The process of finding the derivative is called differentiation. The inverse process is called anti-differentiation. Let’s find the derivative of a function y = f(x).
Example: Find the derivative of the following functions from first principle (x−1)(x−2)
Solution
Let f(x)=(x−1)(x−2)
Thus according to first principle,
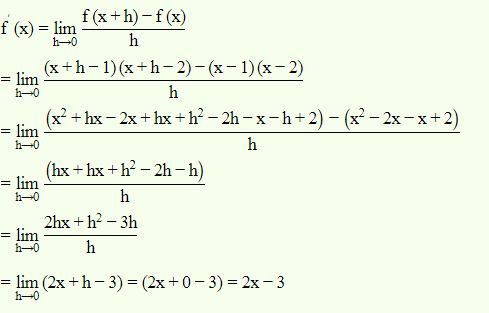
Example Find the derivative of f(x) = 10x.
Solution Since
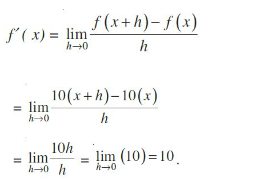
Example Compute the derivative of tan x.
Solution Let f(x) = tan x. Then f’(x) =
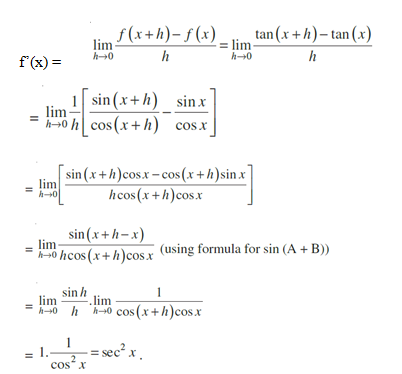
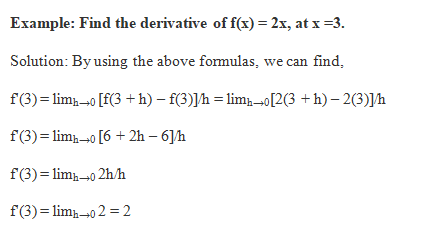
Note:
- D(y) or D[f(x)] is called Euler’s notation.
- dy/dx is called Leibniz’s notation.
F’(x) is called Lagrange’s notation
Formula
- If f(x) = tan (x), then f'(x) = sec2x
- If f(x) = cos (x), then f'(x) = -sin x
- If f(x) = sin (x), then f'(x) = cos x
- If f(x) = ln(x), then f'(x) = 1/x
- If f(x) = ex, then f'(x) = ex
- If f(x) = xn, where n is any fraction or integer, then f'(x) = nxn-1
- If f(x) = k, where k is a constant, then f'(x) = 0
Algebra of derivative of functions:
Let two functions of x be u(x) and v(x)
The basic differentiation rules that need to be followed are as follows:
[1] Sum and Difference Rule
If the function is the sum or difference of two functions, the derivative of the functions is the sum or difference of the individual functions, i.e.,
If f(x) = u(x) ± v(x) then, f'(x) =(d/dx)[u(x)+v(x)] =u'(x) ± v'(x)
[2] Product Rule
If the function f(x) is product of two functions u(x) and v(x), the derivative of the function is,
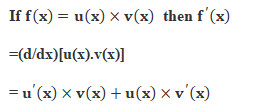
[3] Quotient Rule
If the function f(x) is in the form of two functions [u(x)]/[v(x)], the derivative of the function is

[4] Chain Rule
If a function y = f(x) = g(u) and if u = h(x), then the chain rule for differentiation is defined as,
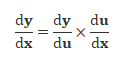

Example: Differentiate f(x) = 6x3 – 9x + 4 with respect to x.
Solution: Given: f(x) = 6x3 – 9x + 4
On differentiating both the sides w.r.t x, we get;
f'(x) = (3)(6)x2 – 9
f'(x) = 18x2 – 9
General Derivative Formulas


5. The derivative of the sum, difference, quotient, and product of functions
- Books Name
- AMARENDRA PATTANAYAK Mathmatics Book
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 11
- Subject
- Mathmatics
The derivative of the sum, difference, quotient, and product of functions
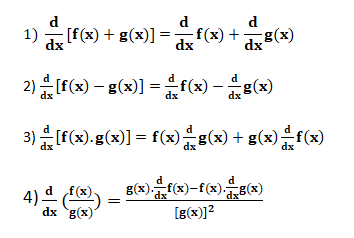
Example: Find derivative of y= x2+3x-5
Ans:
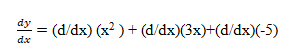
=2x +3
Example: Find derivative of y=( x2+3x)(2x-7)
Ans:
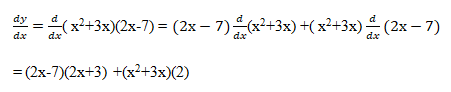
Example: Find derivative of y=( x2+3x)/(2x-7)
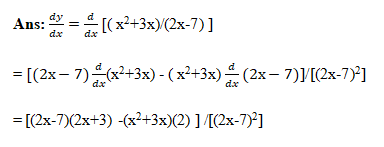
Example : Find the derivative of sin x – cos x.
Solution:
Given function is: sin x – cos x
Let f(x) = sin x and g(x) = cos x
Using the difference rule of differentiation,
d/dx [f(x) – g(x)] = d/dx f(x) – d/dx g(x)
d/dx (sin x – cos x) = d/dx (sin x) – d/dx (cos x)
= cos x – (-sin x)
= cos x + sin x
Example : Find the derivative of (5x3 – 3x + 1)(x + 1).
Solution:
Given: (5x3 – 3x + 1)(x + 1)
Let f(x) = (5x3 – 3x + 1) and g(x) = (x + 1)
Using the product rule of differentiation,
d/dx [f(x) .g(x)] = f(x) [d/dx g(x)] + g(x) [d/dx f(x)]
= (5x3 – 3x + 1) [d/dx (x + 1)] + (x + 1) [d/dx (5x3 – 3x + 1)]
= (5x3 – 3x + 1) (1 + 0) + (x + 1)[5(3x2) – 3(1) + 0]
= (5x3 – 3x + 1) + (x + 1)(15×2 – 3)
= 5x3 – 3x + 1 + 15x3 – 3x + 15x2 – 3
= 20x3 + 15x2 – 6x – 2
6. Derivatives of polynomial and trigonometric functions
- Books Name
- AMARENDRA PATTANAYAK Mathmatics Book
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 11
- Subject
- Mathmatics
Derivatives of polynomial and trigonometric functions
Example: Compute derivative of f(x) = sin 2x
Ans: f’(x) = ![]()
= 2sinx(-sinx) + 2cosx cosx
= -2sin2x + 2cos2x
= 2 cos2x
Examples: ![]()
Solution:
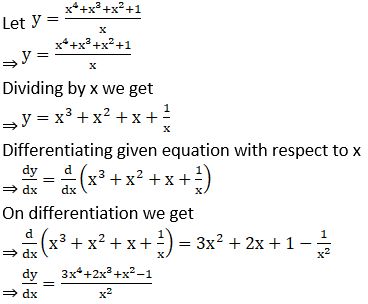
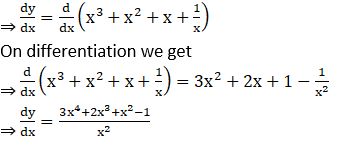
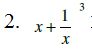
Solution:
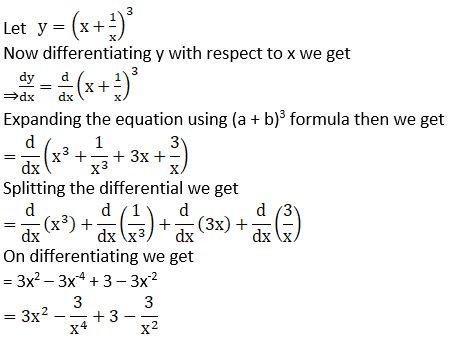
3. (3x + 5) (1 + tan x)
Solution:
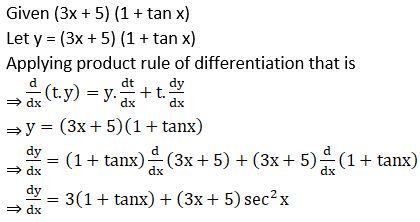
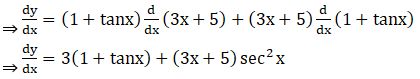
4. (sec x – 1) (sec x + 1)
Solution:
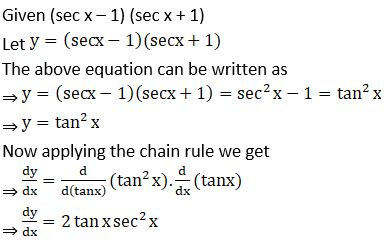
![]()
Solution:

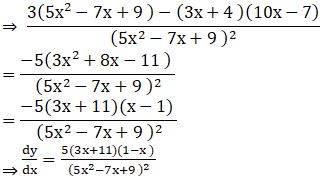
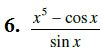
Solution:


 KRISHNA PUBLICATIONS
KRISHNA PUBLICATIONS
