2. Distance between 2 points, section formula

Distance between 2 points, section formula

Distance between Two Points

If P (x1, y1, z1) and Q (x2, y2, z2) are the two points, then the distance between P and Q is given by:

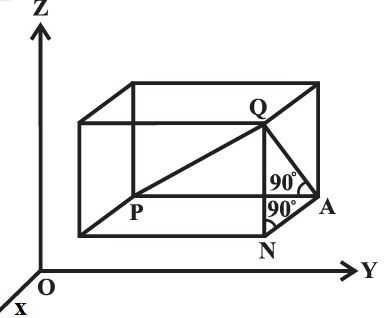
Now PA = y2 – y1, AN = x2 – x1 and NQ = z2 – z1

Hence PQ² = (x2 – x1)² + (y2 – y1) ²+ (z2 – z1) ²

Therefore PQ =  √ [(x2 – x1)² + (y2 – y1) ²+ (z2 – z1) ² ]This gives us the distance between two points (x1, y1, z1) and (x2, y2, z2).

In particular, if x1 = y1 = z1 = 0, i.e., point P is origin O, then OQ =  √(x2² + y2² + z2²)

which gives the distance between the origin O and any point Q (x2, y2, z2).

PQ=(x2-x1)2+(y2-y1)2+(z2-z1)2

Section Formula

Example : Find the equation of set of points P such that PA² + PB² = 2k², where A and B are the points (3, 4, 5) and (–1, 3, –7), respectively.

Solution Let the coordinates of point P be (x, y, z).

Here PA² = (x – 3) ² + (y – 4) ² + ( z – 5) ²

PB² = (x + 1) ² + (y – 3) ² + (z + 7) ²

By the given condition PA² + PB² = 2k², we have

(x – 3) ² + (y – 4) ² + (z – 5) ² + (x + 1) ² + (y – 3) ² + (z + 7) ² = 2k²

i.e., 2x² + 2y² + 2z² – 4x – 14y + 4z = 2k² – 109.

 Let the two given points be P(x1, y1, z1) and Q (x2, y2, z2). Let the point R (x, y, z) divide PQ in the given ratio m : n internally

To determine the coordinates of the point P, the following steps are followed:

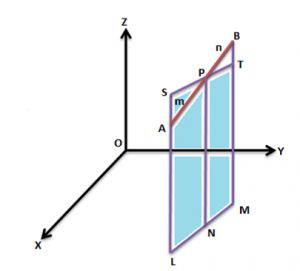
• Draw AL, PN, and BM perpendicular to XY plane such that AL || PN || BM as shown above.
• The points L, M and N lie on the straight line formed due to the intersection of a plane containing AL, PN and BM and XY- plane.
• From point P, a line segment ST is drawn such that it is parallel to LM.
• ST intersects AL externally at S, and it intersects BM at T internally.

Since ST is parallel to LM and AL || PN || BM, therefore, the quadrilaterals LNPS and NMTP qualify as parallelograms.

Also, ∆ASP ~∆BTP therefore,

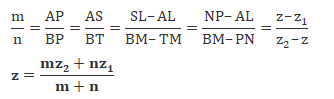
Rearranging the above equation we get,

Sectional Formula (Internally)

Thus, the coordinates of the point P(x, y, z) dividing the line segment joining the points A(x₁, y₁, z₁) and B(x₂, y₂, z₂) in the ratio m:n internally are given by:

Sectional Formula (Externally)

If the given point P divides the line segment joining the points A(x₁, y₁, z₁) and B(x₂, y₂, z₂) externally in the ratio m:n, then the coordinates of P are given by replacing n with –n as:

This represents the section formula for three dimension geometry.

If the point P divides the line segment joining points A and B internally in the ratio k:1, then the coordinates of point P will be

What if the point P dividing the line segment joining points A(x₁, y₁, z₁) and B(x₂, y₂, z₂) is the midpoint of line segment AB?

In that case, if P is the midpoint, then P divides the line segment AB in the ratio 1:1, i.e. m=n=1. Coordinates of point P will be given as:

Therefore, the coordinates of the midpoint of line segment joining points A(x₁, y₁, z₁) and B(x₂, y₂, z₂) are given by,

If the point R divides PQ externally in the ratio m : n, then its coordinates are obtained by replacing n by – n so that coordinates of point R will be

The above procedure can be repeated by drawing perpendiculars to XZ and YZ- planes to get the x and y coordinates of the point P that divides the line segment AB in the ratio m:n internally.

Sectional Formula (Internally)

Thus, the coordinates of the point P(x, y, z) dividing the line segment joining the points A(x₁, y₁, z₁) and B(x₂, y₂, z₂) in the ratio m:n internally are given by:

Sectional Formula (Externally)

If the given point P divides the line segment joining the points A(x₁, y₁, z₁) and B(x₂, y₂, z₂) externally in the ratio m:n, then the coordinates of P are given by replacing n with –n as:

This represents the section formula for three dimension geometry.

If the point P divides the line segment joining points A and B internally in the ratio k:1, then the coordinates of point P will be

What if the point P dividing the line segment joining points A(x₁, y₁, z₁) and B(x₂, y₂, z₂) is the midpoint of line segment AB?

In that case, if P is the midpoint, then P divides the line segment AB in the ratio 1:1, i.e. m=n=1.

Coordinates of point P will be given as:

Therefore, the coordinates of the midpoint of line segment joining points A(x₁, y₁, z₁) and B(x₂, y₂, z₂) are given by,

If the point R divides PQ externally in the ratio m : n, then its coordinates are obtained by replacing n by – n so that coordinates of point R will be