2. Conditions for parallelism and perpendicularity of lines and Collinearity of three points

Conditions for parallelism and perpendicularity of lines and Collinearity of three points:

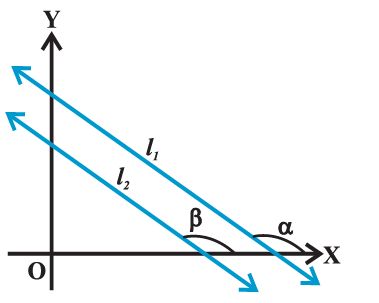
In a coordinate plane, suppose that non-vertical lines l1 and l2 have slopes m1

and m2, respectively. Let their inclinations be a and b, respectively.

If the line l1 is parallel to l2 (Fig 10.4), then their

inclinations are equal, i.e.,a = b, and hence, tan a = tan b

Therefore m1 = m2, i.e., their slopes are equal.

Conversely, if the slope of two lines l1 and l2 is same,

i.e., m1 = m2.

Then   tan a = tan b.

By the property of tangent function (between 0° and 180°), a = b.

Therefore, the lines are parallel.

Hence, two non vertical lines l1 and l2 are parallel if and only if their slopes are equal.

If the lines l1 and l2 are perpendicular , then b = a + 90°.

Therefore, tan b = tan (a + 90°)

= – cot a = -1/ tan a

i.e., m₁= -1/m₂   or m₁ m₂ = -1

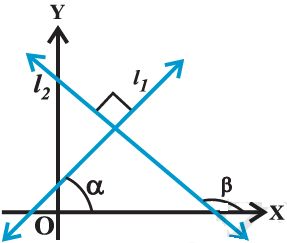
Conversely, if m1 m2 = – 1, i.e., tan a tan b = – 1.

Then tan a = – cot b = tan (b + 90°) or tan (b – 90°)

Therefore, a and b differ by 90°.

Thus, lines l1 and l2 are perpendicular to each other.

Hence, two non-vertical lines are perpendicular to each other if and only if their slopes are negative reciprocals of each other,

Example:  Line through the points (–2, 6) and (4, 8) is perpendicular to the line

through the points (8, 12) and (x, 24). Find the value of x.

Solution: Slope of the line through the points (– 2, 6) and (4, 8) is

m = (8 – 6) /(4  – (-2)) = 2 / 6 = 1/ 3

Slope of the line through the points (8, 12) and (x, 24) is

m = (24 – 12) /(x – 8) = 12 / (x-8)

Since two lines are perpendicular,

m1 m2 = –1, which gives

• [12 / (x-8)] . [1 / 3] = - 1
• 4 / ( x – 8 ) = - 1
•  x – 8 = - 4
• x = 4

Angle between two lines

Let L1 and L2 be two non-vertical lines with slopes m1 and m2, respectively. If a1 and a2 are the inclinations of lines L1 and L2, respectively. Then m₁= tan a1 and m₂=tana2

Let q and f be the adjacent angles between the lines L1 and L2 . Then q = α₂ - a1  and a1, a2 ¹ 90^o

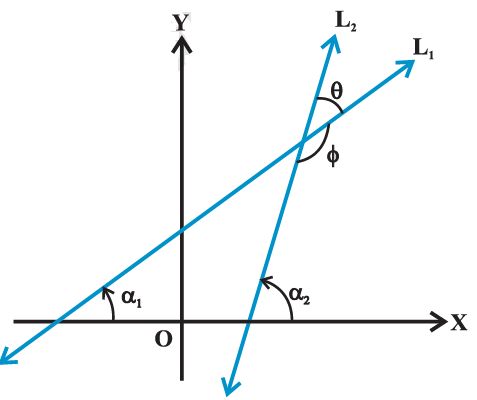
Therefore tan q = tan (a2 – a1) =[ tana2 – tana1] / [1+ tana2 –tana1] = [m₂-m₁] / [1+ m₁m₂]

(as 1 + m1m2 ¹ 0)

and  f = 180° – q so that

tan f = tan (180° – q ) = – tan q = - [m₂-m₁] / [1+ m₁m₂] (as 1 + m1m2 ¹ 0)

Now, there arise two cases:

which means that q will be obtuse and f will be acute.

Thus, the acute angle (say q) between lines L1 and L2 with slopes m1 and m2,

respectively, is given by

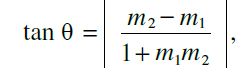
……………………(1)

The obtuse angle (say f) can be found by using  f =180⁰ – q.

Example: If P (-2, 1), Q (2, 3) and R (-2, -4) are three points, find the angle between the straight lines PQ and QR.

The slope of PQ is given by

m = ( y₂ – y₁ ) / (x₂ – x₁)

m =( 3 – 1 ) / (2 – (-2 ))

m= 2/4

Therefore, m₁=1/2

The slope of QR is given by

m= (−4−3) / (−2−2)

m= 7/4

Therefore, m₂ = 7/4

Substituting the values of m₂ and m₁ in the formula for the angle between two lines when we know the slopes of two sides, we have,

tan θ=± (m₂ – m₁ ) / (1+m₁m₂)

tan θ=± ((7/4) – (1/2) ) / (1+ (1/2)(7/4))

tan θ=± (2/3)

Therefore,  θ = tan ^-1 (⅔)

Co linearity of three points

 We know that slopes of two parallel lines are equal. If two lines having the same slope pass through a common point, then two lines will coincide. Hence, if A, B and C are three points in the XY-plane, then they will lie on a line, i.e., three points are collinear  if and only if

slope of AB = slope of BC.

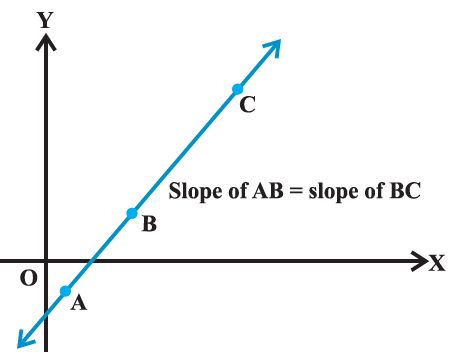
Example: Three points P (h, k), Q (x1, y1) and R (x2, y2) lie on a line. Show that

(h – x1) (y2 – y1) = (k – y1) (x2 – x1).

Solution : Since points P, Q and R are collinear, we have

Slope of PQ = Slope of QR,

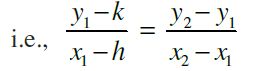
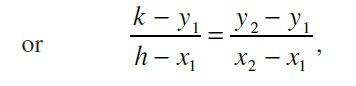
or   (h – x1) (y2 – y1) = (k – y1) (x2 – x1).