1. Cartesian Products of Sets

Chapter 2

Relation and Function

Cartesian Product / Product Simply:

After French philosopher, mathematician and Scientists René Descartes (1596-1650),whose formulation of analytic geometry gave rise to the concept.

In 17^th century the invention of Cartesian coordinates system by Rene Descartes( Latin name: cartesius) revolutionized mathematics by providing the first systematic link between  Euclidean Geometry and Algebra

Who invented the Cartesian product?

René Descartes invented the Cartesian product. It derives the name from the same person. René formulated analytic geometry which helped in the origination of this concept which we further generalize in terms of direct product.

An ordered pair means that two elements are taken from each set.’

 For two non-empty sets (say A & B), the first element of the pair is from one set A and the second element is taken from the second set B.

If {a,b} is a set consisting of the elements of a,b, it is called pair.

If we specify a to be the first element and b to be the second element , then we call {a,b} an order pair and Write it as (a,b).

Cartesian Products of Sets:

Let A and B be the two sets such that A is a set of three colors of tables and B is a set of three colors of chairs objects, i.e.,

A = {brown, green, yellow}

B = {red, blue, purple},

Let’s find the number of pairs of colored objects that we can make from a set of tables and chairs in different combinations. They can be paired as given below:

(brown, red), (brown, blue), (brown, purple), (green, red), (green, blue), (green, purple), (yellow, red), (yellow, blue), (yellow, purple)

There are nine such pairs in the Cartesian product since three elements are there in each of the defined sets A and B. The above-ordered pairs represent the definition for the Cartesian product of sets given. This product is denoted by “A × B”.

Suppose there are two non-empty sets A and B.

So, the Cartesian product of A and B is the set of all ordered pairs of elements from A and B.

i.e., A × B = {(a , b) : a ∊ A, b ∊ B}

Example: Let A = {a_1,a_2,a₃,a₄} and B = {b₁,b₂}

Then, The Cartesian product of A and B will be;

A × B = {(a_1,b₁₎, (a_2,b₁),( a_3,b₁),( a_4,b₁).( a_1,b₂),( a_2,b₂),( a_3,b₂),( a_4,b₂ )}

Example: Let us say, A = {1,2} and B = { a,b,c}

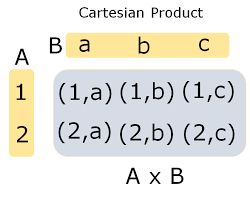
Therefore, A × B = {(1,a),(1,b),(1,c),(2,a),(2,b),(2,c)}.

This set has 8 ordered pairs. We can also represent it as in a tabular form.

Note: Two ordered pair X and Y are equal, if and only if the corresponding first elements and second elements are equal.

Example: Suppose, A = {cow, horse} B = {egg, juice}

 then, A×B = {(cow, egg), (horse, juice), (cow, juice), (horse, egg)}

If either of the two sets is a null set, i.e., either A = Φ or B = Φ, then, A × B = Φ i.e., A × B will also be a null set

Number of Ordered Pairs

For two non-empty sets, A and B. If the number of elements of A is p

 i.e., n(A) = p & that of B is q

 i.e., n(B) = q,

then the number of ordered pairs in Cartesian product will be n(A × B) = n(A) × n(B) = pq.

Properties:

1. The Cartesian Product is non-commutative: A × B ≠ B × A.
2. The cardinality of the Cartesian Product is defined as the number of elements in A × B and is equal to the product of cardinality of both sets:

|A × B| = |A| * |B|

3. A × B = ∅, if either A = ∅ or B = ∅
4. If (x,y) = (a,b) ,then x=a , y=b
5. A×B=B×A, if only A=B
6. The Cartesian product is associative:

(A×B)×C=A×(B×C). It means the Cartesian product of the three-set is the same, i.e., it doesn’t depend upon which bracket is multiplied first as the final result will be the same.

7. Distributive property over a set intersection:

A×(B∩C)=(A×B)∩(A×C)

8.  Distributive property over set union:

A×(B∪C)=(A×B)∪(A×C)

9.  If A⊆B, then A×C⊆B×C for any set C.
10. AxBxC  = {(a,b,c) : aÎA, bÎ B ,cÎ C}

Here (a,b,c) is called ordered triplet.

Solved Examples:

1. Let A = {–1, 2, 3} and B = {1, 3}. Determine
(i) A × B

(ii) B × A
(iii) B × B

(iv) A × A

Solution:

According to the question,

A = {–1, 2, 3} and B = {1, 3}

(i) A × B

{–1, 2, 3} × {1, 3}

So, A × B = {(–1, 1), (–1, 3), (2, 1), (2, 3), (3, 1), (3, 3)}

Hence, the Cartesian product = {(–1, 1), (–1, 3), (2, 1), (2, 3), (3, 1), (3, 3)}

(ii) B × A.

{1, 3} × {–1, 2, 3}

So, B × A = {(1, –1), (1, 2), (1, 3), (3, –1), (3, 2), (3, 3)}

Hence, the Cartesian product = {(1, –1), (1, 2), (1, 3), (3, –1), (3, 2), (3, 3)}

(iii) B × B

{1, 3} ×{1, 3}

So, B × B = {(1, 1), (1, 3), (3, 1), (3, 3)}

Hence, the Cartesian product = {(1, 1), (1, 3), (3, 1), (3, 3)}

(iv) A × A

{–1, 2, 3} × {–1, 2, 3}

So, A × A = {(–1, –1), (–1, 2), (–1, 3), (2, –1), (2, 2), (2, 3), (3, –1), (3, 2), (3, 3)}

Hence,

the Cartesian product ={(–1, –1), (–1, 2), (–1, 3), (2, –1), (2, 2), (2, 3), (3, –1), (3, 2), (3, 3)}

2. If P = {x : x < 3, x ∈ N}, Q = {x : x ≤ 2, x ∈ W}. Find (P ∪ Q) × (P ∩ Q), where W is the set of whole numbers.

Solution:

According to the question,

P = {x: x < 3, x ∈N}, Q = {x : x ≤ 2, x ∈W} where W is the set of whole numbers

P = {1, 2}

Q = {0, 1, 2}

Now

(P∪Q) = {1, 2}∪{0, 1, 2} = {0, 1, 2}

And,

(P∩Q) = {1, 2}∩{0, 1, 2} = {1, 2}

We need to find the Cartesian product of (P∪Q) = {0, 1, 2} and (P∩Q) = {1, 2}

So,

(P∪Q) × (P∩Q) = {0, 1, 2} × {1, 2}

= {(0, 1), (0, 2), (1, 1), (1, 2), (2, 1), (2, 2)}

Hence, the Cartesian product = {(0, 1), (0, 2), (1, 1), (1, 2), (2, 1), (2, 2)}

3. If A = {x : x ∈ W, x < 2}, B = {x : x ∈ N, 1 < x < 5}, C = {3, 5} find
(i) A × (B ∩ C)
(ii) A × (B ∪ C)

Solution:

According to the question,

A = {x: x ∈ W, x < 2}, B = {x : x ∈N, 1 < x < 5} C = {3, 5}; W is the set of whole numbers

A = {x: x ∈ W, x < 2} = {0, 1}

B = {x : x ∈N, 1 < x < 5} = {2, 3, 4}

(i)

(B∩C) = {2, 3, 4} ∩ {3, 5}

(B∩C) = {3}

A × (B∩C) = {0, 1} × {3} = {(0, 3), (1, 3)}

Hence, the Cartesian product = {(0, 3), (1, 3)}

(ii)

(B∪C) = {2, 3, 4} ∪ {3, 5}

(B∪C) = {2, 3, 4, 5}

A × (B∪C) = {0, 1} × {2, 3, 4, 5} = {(0, 2), (0, 3), (0, 4), (0, 5), (1, 2), (1, 3), (1, 4), (1, 5)}

Hence, the Cartesian product = {(0, 2), (0, 3), (0, 4), (0, 5), (1, 2), (1, 3), (1, 4), (1, 5)}

 

4. : The Cartesian product A × A has 9 elements among which are found (–1, 0) and (0,1). Find the set A and the remaining elements of A × A.

Solution:

We know that,

If n(A) = p and n(B) = q, then n(A × B) = pq

From the given,

n(A × A) = 9

n(A) × n(A) = 9,

n(A) = 3 ……(i)

The ordered pairs (-1, 0) and (0, 1) are two of the nine elements of A × A.

Therefore, A × A = {(a, a) : a ∈ A}

Hence, -1, 0, 1 are the elemets of A. …..(ii)

From (i) and (ii),

A = {-1, 0, 1}

The remaining elements of set A × A are (-1, -1), (-1, 1), (0, -1), (0, 0), (1, -1), (1, 0) and (1, 1).