2. Relations and Types of Relations

Relations and Types of Relations

Relation:

Relation is association between two well-defined  objects.

Relation  in real life give us the link between any two objects or entities. In our daily life, we come across many patterns and links that characterize relations such as a relation of a father and a son, brother and sister, etc.

Relations can be represented in different forms such as arrow representation, algebraic form, set-builder form, graphically, roster form, and tabular form. 

Definition:

Let A and B be two non empty sets.

Then R  :  A ® B  is said to be a relation if R Í AxB .

The element of A (first element) of AxB in the relation is called Domain or Pre-image of relation R.

The element of B (second element) of AxB in the relation is called Range or image of relation R.

The whole B set of AxB in the relation is called Codomain of relation R.

Range Í Codomain

Example : Define a relation R from A to A = {1, 2, 3, 4, 5, 6} as R = {(x, y) : y = x + 1}. Determine the domain, codomain and range of R.

Solution: We can see that A = {1, 2, 3, 4, 5, 6} is the domain and codomain of R.

To determine the range, we determine the values of y for each value of x, that is, when x = 1, 2, 3, 4, 5, 6

• • x = 1, y = 1 + 1 = 2;
  • x = 2, y = 2 + 1 = 3;
  • x = 3, y = 3 + 1 = 4;
  • x = 4, y = 4 + 1 = 5;
  • x = 5, y = 5 + 1 = 6;
  • x = 6, y = 6 + 1 = 7.

Since 7 does not belong to A and the relation R is defined on A, hence, x = 6 has no image in A.

Therefore range of R = {2, 3, 4, 5, 6}

Answer: Domain = Codomain = {1, 2, 3, 4, 5, 6}, Range = {2, 3, 4, 5, 6}

Types of Relations

Given below is a list of different types of relations:

1. Empty Relation
2. Universal Relation
3. Identity Relation
4. Inverse Relation
5. Reflexive Relation
6. Symmetric Relation
7. Transitive Relation
8. Equivalence Relation

1) Empty Relation - A relation is an empty relation if it has no elements, that is, no element of set A is mapped or linked to any element of A. It is denoted by R = ∅.

For example, if set A = {1, 2, 3} then, one of the void relations can be R = {x, y} where, |x – y| = 8. For empty relation,

R = φ ⊂ A × A

2) Universal Relation - A relation R in a set A is a universal relation if each element of A is related to every element of A, i.e., R = A × A. It is called the full relation.

Consider set A = {a, b, c}. Now one of the universal relations will be R = {x, y} where, |x – y| ≥ 0. For universal relation,

R = A × A

3) Identity Relation - A relation R on A is said to be an identity relation if each element of A is related to itself, that is, R = {(a, a) : for all a ∈ A}

 For example, in a set A = {a, b, c}, the identity relation will be I = {a, a}, {b, b}, {c, c}. For identity relation,

I = {(a, a), a ∈ A}

4) Inverse Relation - Define R to be a relation from set P to set Q i.e., R ∈ P × Q. The relation R-1 is said to be an Inverse relation if R-1 from set Q to P is denoted by R^-1 = {(q, p): (p, q) ∈ R}.

For example if set A = {(a, b), (c, d)}, then inverse relation will be R^-1 = {(b, a), (d, c)}. So, for an inverse relation,

R^-1 = {(b, a): (a, b) ∈ R}

5) Reflexive Relation - A binary relation R defined on a set A is said to be reflexive if, for every element a ∈ A, we have aRa, that is, (a, a) ∈ R.

 For example, consider a set A = {1, 2,}. Now an example of reflexive relation will be R = {(1, 1), (2, 2), (1, 2), (2, 1)}. The reflexive relation is given by-

(a, a) ∈ R

6) Symmetric Relation - A binary relation R defined on a set A is said to be symmetric if and only if, for elements a, b ∈ A, we have aRb, that is, (a, b) ∈ R, then we must have bRa, that is, (b, a) ∈ R.

 An example of symmetric relation will be R = {(1, 2), (2, 1)} for a set A = {1, 2}. So, for a symmetric relation,

aRb ⇒ bRa, ∀ a, b ∈ A

Example: For the set P={a,b}, the relation R={(a,b),(b,a)} is called symmetric relation, where a,b∈P.

7) Transitive Relation - A relation R is transitive if and only if (a, b) ∈ R and (b, c) ∈ R ⇒ (a, c) ∈ R for a, b, c ∈ A

Example: For the set A ={a,b,c}, the relation R={(a,b),(b,c),(a,c)} is called transitive relation, where a,b,c∈ A.

8) Equivalence Relation - A relation R defined on a set A is said to be an equivalence relation if and only if it is reflexive, symmetric and transitive.

Conditions:

1. If the relation (R) is reflexive, then all the elements of set A are mapped with itself, such that for every x∈ A , then (x,x)∈R.

2. The relation (R) is symmetric on set A, if (x,y)∈R, then (y,x)∈R, such that a,b∈ A.

3. The relation R on set A, if (x,y)∈R and (y,z)∈R, then (x,z)∈R, for all a,b,c∈ A is called transitive relation

Other Types of Relations:

The other types of relations based on mapping of two sets are given as follows:

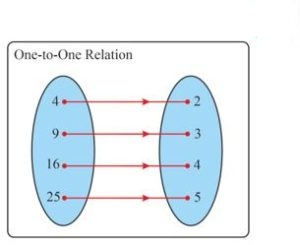
1) One to One Relations

A relation is said to be a One to One relation if all the distinct elements of one set are related or mapped to distinct elements of another set.

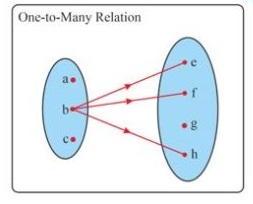
2) One to Many Relations

A relation is said to be One to Many relations if the one element of first set is mapped to more than one element second set.

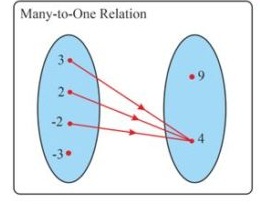
3) Many to One Relation

A relation is said to be Many to One relation if  the more than one element of first set is mapped to one element second set.

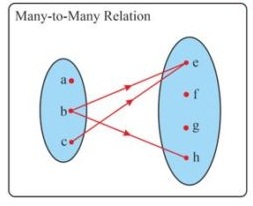
4) Many to Many Relation

A relation is said to be Many to Many relation if  the more than one element of first set is mapped to more than one element second set.

Solved Examples:

Q.1. Let A be the set of two male persons in a family. R be a relation defined onset A is “is a brother of”, check whether R is symmetric or not?

Ans:

Let a,b are two persons in a family, then a,b∈A.

The given relation on set “is a brother of”.

If a is the brother of b, then b is also the brother of a.

R={(a,b),(b,a)}

Hence, the relation R is symmetric.

Q.2. Find the inverse relation of R={(1,2),(3,4),(5,6)}.

Ans:

Given relation is R={(1,2),(3,4),(5,6)}.

Consider R={(a,b):a∈P,b∈Q}. be the relation from set P to set Q, then the relation from set Q to set P is known as inverse relation, such that R–1:Q→P={(a,b):(a,b)∈R}.

So, inverse relation is obtained by taking the reverse of the given ordered pairs.

R–1:{(2,1),(4,3),(6,5)}

Q.3. Find the identity relation on the set P={x,y,z}.

Ans:

We know that the relation (I) is identity, then all the elements of set P are related with itself, such that for every a∈P, then (a,a)∈I.

Given set is P={x,y,z}

Then the identity relation is given by I={(x,x),(y,y),(z,z)}.

Q.4. Let P={1,2,3},R be a relation defined on set P as “is greater than” and R={(2,1),(3,2),(3,1)}. Verify R is transitive.

Ans:

Given set P={1,2,3},

Let P={1,2,3}, then we have

(b,a)=(2,1)→2 is greater than 1.

(c,b)=(3,2)→3 is greater than 2.

(c,a)=(3,1)→3 is greater than 1.

Thus in a transitive relation, if (x,y)∈R,(y,z)∈R, then (x,z)∈R.

So, the relation R={(2,1),(3,2),(3,1)} is transitive.

Q.5. Let set A contains the bag of red balls. Then the relation R of getting white balls from the bag of red balls is what type of relation?

Ans:

Given set A contains the bag contains the red balls. From the bag of red balls, relation R of getting the white ball is not possible. So, the given relation is an empty relation.

Q6. Given R = {(x, y) : x, y ∈ W, x² + y² = 25}. Find the domain and Range of R.

Ans:

According to the question,

R = {(x, y) : x, y ∈W, x² + y² = 25}

R = {(0,5), (3,4), (4, 3), (5,0)}

The domain of R consists of all the first elements of all the ordered pairs of R.

Domain of R = {0, 3, 4, 5}

The range of R contains all the second elements of all the ordered pairs of R.

Range of R = {5, 4, 3, 0}

Q7. If R₁ = {(x, y) | y = 2x + 7, where x ∈ R and – 5 ≤ x ≤ 5} is a relation. Then find the domain and Range of R₁.

Ans:

According to the question,

R₁ = {(x, y) | y = 2x + 7, where x ∈R and – 5 ≤ x ≤ 5} is a relation

The domain of R₁ consists of all the first elements of all the ordered pairs of R₁, i.e., x,

It is also given – 5 ≤ x ≤ 5.

Therefore,

Domain of R₁ = [–5, 5]

The range of R contains all the second elements of all the ordered pairs of R₁, i.e., y

It is also given y = 2x + 7

Now x ∈ [–5,5]

Multiply LHS and RHS by 2,

We get,

2x ∈ [–10, 10]

Adding LHS and RHS with 7,

We get,

2x + 7 ∈ [–3, 17]

Or, y ∈ [–3, 17]

So,

Range of R₁ = [–3, 17]

Q.8. If R₂ = {(x, y) | x and y are integers and x² + y² = 64} is a relation. Then find R₂.

Ans:

We have,

R₂ = {(x, y) | x and y are integers and x² + y² – 64}

So, we get,

x² = 0 and y² = 64 or x² = 64 and y² = 0

x = 0 and y = ±8 or x = ±8 and y = 0

Therefore, R₂ = {(0, 8), (0, –8), (8,0), (–8,0)}

Q.9. If R₃ = {(x, |x| ) |x is a real number} is a relation. Then find domain and range of R₃.

Ans:

According to the question,

R₃ = {(x, |x|) |x is a real number} is a relation

Domain of R₃ consists of all the first elements of all the ordered pairs of R₃, i.e., x,

It is also given that x is a real number,

So, Domain of R₃ = R

Range of R contains all the second elements of all the ordered pairs of R₃, i.e., |x|

It is also given that x is a real number,

So, |x| = |R|

⇒ |x|≥0,

i.e., |x| has all positive real numbers including 0

Hence,

Range of R₃ = [0, ∞)

Q.10: Assume that A = {1, 2, 3,…,14}. Define a relation R from A to A by R = {(x, y) : 3x – y = 0, such that x, y ∈ A}. Determine and write down its range, domain, and codomain.

Solution:

It is given that the relation R from A to A is given by R = {(x, y): 3x – y = 0, where x, y ∈ A}.

It means that R = {(x, y) : 3x = y, where x, y ∈ A}

Hence, R = {(1, 3), (2, 6), (3, 9), (4, 12)}

We know that the domain of R is defined as the set of all first elements of the ordered pairs in the given relation.

Hence, the domain of R = {1, 2, 3, 4}

To determine the codomain, we know that the entire set A is the codomain of the relation R.

Therefore, the codomain of R = A = {1, 2, 3,…,14}

As it is known that, the range of R is defined as the set of all second elements in the relation ordered pair.

Hence, the Range of R is given by = {3, 6, 9, 12}