3. Combinations and Simple applications

Combinations and Simple applications

Combinations:

Let us now assume that there is a group of 3 lawn tennis players X, Y, Z. A team consisting of 2 players is to be formed. In how many ways can we do so? Is the team of X and Y different from the team of Y and X ? Here, order is not important.

These are XY, YZ and ZX.

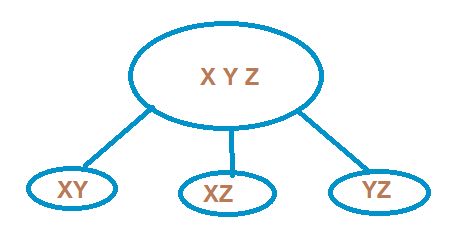
Here, each selection is called a combination of 3 different objects taken 2 at a time.

Definition:

The combination is a selection of a part of a set of objects or a selection of all objects when the order doesn't matter.

or

The number of combinations/selection of n different objects taken r at a time, denoted by ⁿC_r

^{Theorem:   n}P_r= r! . ⁿC_r  , 0 < r  n

Proof: Corresponding to each combination of nCr, we have r ! permutations, because r objects in every combination can be rearranged in r ! ways.

Hence, the total number of permutations of n different things taken r at a time is ⁿP_r= r! . ⁿC_r  .

Properties:

1. ⁿC_r = ⁿC_n-r

2. If ⁿC_r = ⁿC_k, then r = k or n-r = k

3. ⁿC_r + ⁿC_r-1 = ⁿ⁺¹C_r

4. ⁿC_r = n/r  ^n-1C_r-1

5. ⁿC_r/ⁿC_r-1 = (n-r+1)/ r

6. If n is even ⁿC_r is greatest for r = n/2

7. If n is odd, ⁿC_r is greatest for r = (n-1)/2,(n+1)/2

Example; ⁿC₉ = ⁿC₈ then n=?  and ⁿC₁₇=?

Ans: n = a+b = 9+8 =17

ⁿC₁₇= ¹⁷C₁₇=1

Question. In how many ways can a football team of 11 players be selected from 16 players? How many of them will
(i) include 2 particular players?
(ii) exclude 2 particular players?

Solution:

We know that,

ⁿC_r 

According to the question,

11 players can be selected out of 16 = ¹⁶C₁₁

(i) include 2 particular players = ¹⁴C₉

(ii) exclude 2 particular players = ¹⁴C₁₁

Question : Find the number of ways of choosing 4 cards from a pack of 52 playing cards? In how many of these

(i) four cards are of the same suit,

(ii) four cards belong to four different suits,

(iii) are face cards,

(iv) two are red and two are black cards,

(v) cards are of the same colour?

Solution :

There will be a number of possible ways for choosing 4 cards from 52 cards as there are combinations of 52 different things when we take 4 at a time.

Therefore, the required number of ways = ⁵²C₄

= 52! / (4! 48!) = (49x50x51x52) / (2x3x4)

= 270725

(i) Four cards of the same suit:

There are four suits: Spade, heart, Club, diamond. Totally, there are 13 cards of each suit

Therefore, the required number of ways are given by ¹³C₄ + ¹³C₄ + ¹³C₄ + ¹³C₄

= 4(13! / (4! 9! )) = 2860

(ii) four cards belong to four different suits:

Since there are 13 cards in each suit. Therefore choosing 1 card from 13 cards of each suit, it becomes

= ¹³C₁ + ¹³C₁ + ¹³C₁ + ¹³C₁ = 13⁴

(iii) Face cards :

There are 12 face cards and 4 cards are selected from these 12 cards, it becomes

= ¹²C₄

Therefore, the required number of ways = 12! / ( 4! 8!) = 495

(iv) Two red cards and two black cards:

There are 26 red and 26 black cards in a pack of52 cards.

Therefore, the required number of ways = ²⁶C₂ x ²⁶C₂

=

= (325)²

=105625

(v) Cards of the same color:

Out of 26 red cards and 26 black cards, 4 red and black cards are selected in ²⁶C₄ ways. So, the required number of ways = ²⁶C₄ + ²⁶C₄

= 2 (26! / 4! 22! )

=29900.

Question: If the different permutations of all the letter of the word EXAMINATION are listed as in a dictionary, how many words are there in this list before the first word starting with E?

Solution:

In dictionary words are listed alphabetically, so to find the words

Listed before E should start with letter either A, B, C or D

But the word EXAMINATION doesn`t have B, C or D

Hence the words should start with letter A

The remaining 10 places are to be filled by the remaining letters of the word EXAMINATION which are E, X, A, M, 2N, T, 2I, 0

Since the letters are repeating the formula used would be

Where n is remaining number of letters p₁ and p₂ are number of times the repeated terms occurs.

The number of words in the list before the word starting with E

= words starting with letter A = 907200

N.B.:

• The number of ways of selecting r objects from n different objects subject to certain condition like:

1. k particular objects are always included =  ^n-kC_r-k

2. k particular objects are never included =  ^n-kC_r

• The number of arrangement of n distinct objects taken r at a time so that k particular objects are

        (i) Always included = ^n-kC_r-k.r!,

        (ii) Never included = ^n-kC_r.r!.

• In order to compute the combination of n distinct items taken r at a time wherein, the chances of occurrence of any item are not fixed and may be one, twice, thrice, …. up to r times is given by ^n+r-1C_r
• If there are m men and n women (m > n) and they have to be seated or accommodated in a row in such a way that no two women sit together then total no. of such arrangements = ^m+1C_n. m! This is also termed as the Gap Method. 
• If we have n different things taken r at a time in form of a garland or necklace, then the required number of arrangements is given by ⁿC_r(r-1)!/2.
• If there is a problem that requires n number of persons to be accommodated in such a way that a fixed number say ‘p’ are always together, then that particular set of p persons should be treated as one person. Hence, the total number of people in such a case becomes (n-m+1). Therefore, the total number of possible arrangements is (n-m+1)! m! This is also termed as the String Method.  
• Let there be n types of objects with each type containing at least r objects. Then the number of ways of arranging r objects in a row is n^r. 
• The number of selections from n different objects, taking at least one =  ⁿC₁ + ⁿC₂ + ⁿC₃ + ... + ⁿC_n = 2ⁿ - 1.  
• Total number of selections of zero or more objects from n identical objects is n+1.
• Selection when both identical and distinct objects are present: 

The number of selections, taking at least one out of a₁ + a₂ + a₃ + ... a_n + k objects, where a₁ are alike (of one kind), a₂ are alike (of second kind) and so on ... a_n are alike (of nth kind), and k are distinct = {[(a₁ + 1)(a₂ + 1)(a₃ + 1) ... (a_n + 1)]2^k} - 1.

• Combination of n different things taken some or all of n things at a time is given by 2ⁿ – 1. 
• Combination of n things taken some or all at a time when p of the things are alike of one kind, q of the things are alike and of another kind and r of the things are alike of a third kind = [(p + 1) (q + 1)(r + 1)….] – 1.
• The number of ways to select some or all out of (p+q+t) things where p are alike of first kind, q are alike of second kind and the remaining t are different is = (p+1)(q+1)2^t – 1.
• Combination of selecting s₁ things from a set of n₁ objects and s₂ things from a set of n₂ objects where combination of s₁ things and s₂ things are independent is given by ⁿ₁C_s1 x ⁿ₂C_s2  
• Total number of ways in which n identical items which can be distributed among p persons so that each person may get any number of items is ^n+p-1C_p-1.
• Total number of ways in which n identical items can be distributed among p persons such that each them receive at least one item ^n-1C_p-1