2. Permutations and Factorial notation

Permutations and Factorial notation

Factorial notation:    

n! = n(n-1)(n-2) (n-3) …….2x1

n! = n(n-1)! = n(n-1)(n-2)!

0! = 1

1! = 1

5! = 4! x 5  = 3 ! x 4x 5

Question 1: Evaluate  (i) 8! (ii) 4! – 3!

ANSWER:

(i) 8! = 1 × 2 × 3 × 4 × 5 × 6 × 7 × 8 = 40320

(ii) 4! = 1 × 2 × 3 × 4 = 24

3! = 1 × 2 × 3 = 6

∴4! – 3! = 24 – 6 = 18
Question 2: Is 3! + 4! = 7!?

ANSWER:

3! = 1 × 2 × 3 = 6

4! = 1 × 2 × 3 × 4 = 24

∴3! + 4! = 6 + 24 = 30

7! = 1 × 2 × 3 × 4 × 5 × 6 × 7 = 5040

∴ 3! + 4! ≠ 7!

Question 3:  Compute 

ANSWER:

Question 4: If , find x.

ANSWER:

Question 4. How many 5-digit telephone numbers can be constructed using the digits 0 to 9 if each number starts with 67 and no digit appears more than once?

Solution:

Let the five-digit number be ABCDE. Given that first 2 digits of each number is 67. Therefore, the number is 67CDE.

As the repetition is not allowed and 6 and 7 are already taken, the digits available for place C are 0,1,2,3,4,5,8,9. The number of possible digits at place C is 8. Suppose one of them is taken at C, now the digits possible at place D is 7. And similarly, at E the possible digits are 6.

∴The total five-digit numbers with given conditions = 8 × 7 × 6 = 336.

Question 5. A coin is tossed 3 times and the outcomes are recorded. How many possible outcomes are there?

Solution:

Given A coin is tossed 3 times and the outcomes are recorded

The possible outcomes after a coin toss are head and tail.

The number of possible outcomes at each coin toss is 2.

∴The total number of possible outcomes after 3 times = 2 × 2 × 2 = 8.

Question 6. Given 5 flags of different colours, how many different signals can be generated if each signal requires the use of 2 flags, one below the other?

Solution:

Given 5 flags of different colours

We know the signal requires 2 flags.

The number of flags possible for upper flag is 5.

Now as one of the flag is taken, the number of flags remaining for lower flag in the signal is 4.

The number of ways in which signal can be given = 5 × 4 = 20.

Question 7. Evaluate
(i) 8!

(ii) 4! – 3!

Solution:

(i) Consider 8!

We know that 8! = 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1

= 40320

(ii) Consider 4!-3!

4!-3! = (4 × 3!) – 3!

Above equation can be written as

= 3! (4-1)

= 3 × 2 × 1 × 3

= 18

2. Is 3! + 4! = 7!?

Solution:

Consider LHS 3! + 4!

Computing left hand side, we get

3! + 4! = (3 × 2 × 1) + (4 × 3 × 2 × 1)

= 6 + 24

= 30

Again consider RHS and computing we get

7! = 7 × 6 × 5 × 4 × 3 × 2 × 1 = 5040

Therefore LHS ≠ RHS

Therefore 3! + 4! ≠ 7!

Permutations:

A permutation is an arrangement in a definite order of a number of objects taken some or all at a time.

Permutations when all the objects are distinct:

Theorem 1: The number of permutations of n different objects taken r at a time,

where 0 < r n and the objects do not repeat is n ( n – 1) ( n – 2). . .( n – r + 1),

which is denoted by nPr.

Proof There will be as many permutations as there are ways of filling in r vacant places

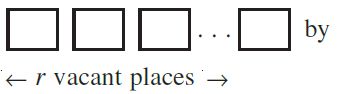
the n objects. The first place can be filled in n ways; following which, the second placecan be filled in (n – 1) ways, following which the third place can be filled in (n – 2)ways,..., the rth place can be filled in (n – (r – 1)) ways. Therefore, the number of ways of filling in r vacant places in succession is n(n – 1) (n – 2) . . . (n – (r – 1)) or n ( n – 1) (n – 2) ... (n – r + 1)

= [n ( n – 1) (n – 2) ... (n – r + 1)(n-r)! ] / (n-r)!  = ⁿp_r = p(n,r)

ⁿp_r =n!n-r! , where 0 < r n

ⁿp_n =n!n!=1

ⁿp₀ =n!0! =n!

Theorem 2 : The number of permutations of n different objects taken r at a time,

where repetition is allowed, is n^r.

i.e., n x n x n x n x n x…r times….x n= n^r

Example: Find the number of 4 letter words, with or without meaning, which can be

formed out of the letters of the word ROSE.

Ans:

The required number of words = ⁴P4 = 4! = 24. Here repetition is not allowed.

If repetition is allowed, the required number of words would be 4⁴ = 256.

Example: The number of 3-letter words which can be formed by the letters of the word

NUMBER =⁶P₃ = 6!/3!= 4 × 5 × 6 = 120.

Here, in this case also, the repetition is not allowed.

 If the repetition is allowed, the required number of words would be 6³ = 216.

Example:

The number of ways in which a Chairman and a Vice-Chairman can be chosen

from amongst a group of 12 persons assuming that one person can not hold more than

one position, clearly ¹²P₂= 12!/10! =11x12=132

Permutations when all the objects are not distinct objects:

Example:

Suppose we have to find the number of ways of rearranging the letters of the word ROOT.

Therefore, the required number of permutations = 4!/2! =3x4= 12

Theorem 3: The number of permutations of n objects, where p objects are of the same kind and rest are all different = n!/p!

Theorem 4: The number of permutations of n objects, where p1 objects are of one

kind, p2 are of second kind, ..., p_k are of k^th kind and the rest, if any, are of different kind is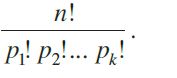  

Example  Find the number of permutations of the letters of the word ALLAHABAD.

Solution Here, there are 9 objects (letters) of which there are 4A’s, 2 L’s and rest are

all different.

Therefore, the required number of arrangements =9!/(4!x2!)= 5x 6 x 7 x 8 x 9  / 2 =7560

Example: 

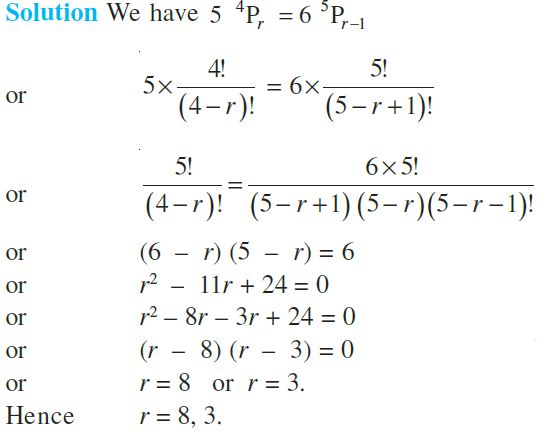
Example: How many words, with or without meaning can be made from the letters of the word MONDAY, assuming that no letter is repeated, if

(i) 4 letters are used at a time, 

(ii) all letters are used at a time, 

(iii) all letters are used but the first letter is a vowel?

Solution:

Given word: MONDAY

(i) Number of letters to be used = 4

Number of permutations = ⁶P₄ = 6!/(6 – 4)! = 6!/2! = 720/2 = 360

Therefore, we can form 350 words with 4 letters from the word MONDAY.

(ii) Number of letters to be used = 6

Number of permutations = ⁶P₆ = 6!/(6 – 6)! = 6!/0! = 720/1 = 720

Therefore, we can form 720 words using all the letters from the word MONDAY.

(iii) Number of vowels in the word MONDAY = 2 (O and A)

Number of ways that the first letter is a vowel = ²P₁ = 2!/(2 – 1)! = 2!/1! = 2

Now, the remaining places = 5

Remaining letters  = 5

These can be arranged in 5! ways, i.e. 120

Therefore, the total number of words can be formed with the first letter as vowel = 2 × 120 = 240.

N.B.:

• Almost all permutation questions involve putting things in order from a line where the order matters. For example ABC is a different permutation to ACB.
• The number of permutations of n distinct objects when a particular object is not to be considered in the arrangement is given by ^n-1P_r.
• The number of permutations of n distinct objects when a specific object is to be always included in the arrangement is given by r.^n-1P_r-1.
• If we need to compute the number of permutations of n different objects, out of which r have to be selected and each object has the probability of occurring once, twice or thrice… up to r times in any arrangement is given by (n)^r.
• Circular permutation is used when some arrangement is to be made in the form of a ring or circle.
• When ‘n’ different or unlike objects are to be arranged in a ring in such a way that the clockwise and anticlockwise arrangements are different, then the number of such arrangements is given by (n – 1)!
• If r things are taken at a time out of n distinct things and arranged along a circle, then the number of ways of doing this is given by ⁿC_r(r-1)!.
• If clockwise and anti-clockwise are considered to be the same, then the total number of circular permutations is given by (n-1)!/2.
• If n persons are to be seated around a round table in such a way that no person has similar neighbor then it is given by ½ (n – 1)!
• The number of necklaces formed with n beads of different colors = ½ (n – 1)!