4. Some Special functions,Domain,Range and their graphs

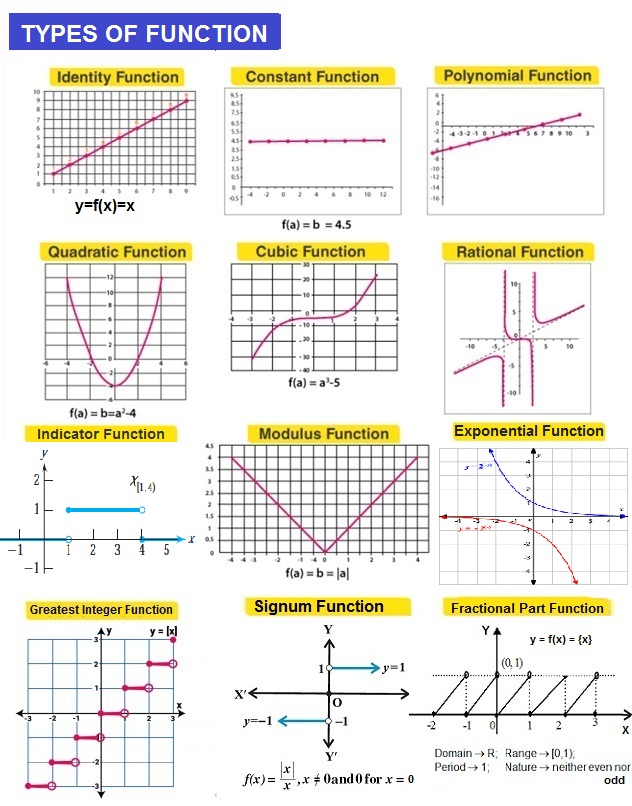
Special Types of Functions

• Constant Function
• Identity Function
• Polynomial function
• Linear Function
• Identical Function
• Quadratic Function
• Rational Function
• Algebraic Functions
• Cubic Function
• Modulus Function
• Signum Function
• Greatest Integer Function
• Smallest Integer Function
• Step Function
• Characteristics Function
• Indicator Function
• Fractional Part Function
• Exponential Function
• Logarithmic Function
•  Sinusoidal. Function
• Even and Odd Function
• Periodic Function
• Composite Function

Polynomial function

A real valued function f : P → P defined by y = f (a)=h₀+h₁ a+…..+h_n a_n, where n ϵ N, and h₀+h₁+…..+h_n ϵ P, for each a ϵ P, is called polynomial function.

• N = a Natural Number.
• The degree of Polynomial function is the highest power in the expression.
• If the degree is zero, it’s called a constant function.
• If the degree is one, it’s called a linear function. Example: b = a+1.
• Graph type: Always a straight line.

So, a polynomial function can be expressed as :

f(x)=a_nx_n+a_n−1x_n−1+…..+a₁x₁+a₀

The highest power in the expression is known as the degree of the polynomial function. The different types of polynomial functions based on the degree are:

1. The polynomial function is called a Constant function if the degree is zero.
2. The polynomial function is called a Linear if the degree is one.
3. The polynomial function is Quadratic if the degree is two.
4. The polynomial function is Cubic if the degree is three.

Linear Function

All functions in the form of ax + b where a, b∈R & a ≠ 0 are called as linear functions. The graph will be a straight line. In other words, a linear polynomial function is a first-degree polynomial where the input needs to be multiplied by m and added to c. It can be expressed by f(x) = mx + c.

For example, f(x) = 2x + 1 at x = 1

f(1) = 2.1 + 1 = 3

f(1) = 3

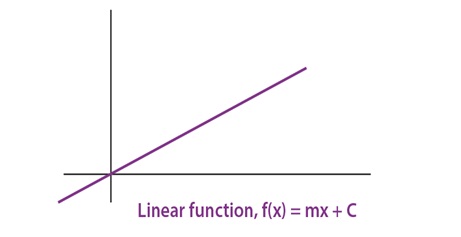
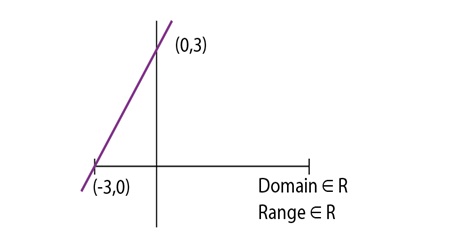
Another example of linear function is y = x + 3

Identical Function

Two functions f and g are said to be identical if

(a) The domain of f = domain of g

(b) The range of f = the Range of g

(c) f(x) = g(x)∀  x∈D_f & D_g

For example f(x) = x & g(x) =11/x

Solution: f(x) = x is defined for all x

But g(x) = 11/x is not defined of x = 0

Hence it is identical for x ∈R -{0}

Quadratic Function

All functions in the form of y = ax² + bx + c where a, b, c∈R, a ≠ 0 will be known as Quadratic function. The graph will be parabolic.

At x=−b±D2, we will get its maximum on minimum value depends on the leading coefficient and that value will be −D4a (where D = Discriminant)

In simpler terms,

A Quadratic polynomial function is a second degree polynomial and it can be expressed as;

F(x) = ax² + bx + c, and a is not equal to zero.

Where a, b, c are constant and x is a variable.

Example, f(x) = 2x² + x – 1 at x = 2

If x = 2, f(2) = 2.2² + 2 – 1 = 9

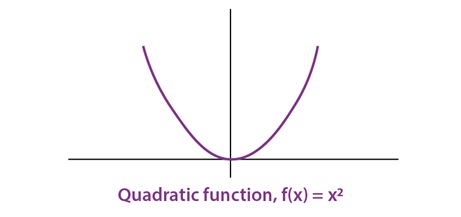
For Example: y = x² + 1

Read More: Quadratic Function Formula

Rational Function

These are the real functions of the type f(a)g(a) where f (a) and g (a) are polynomial functions of a defined in a domain, where g(a) ≠ 0.

• For example f : P – {– 6} → P defined by f (a) = f(a+1)g(a+2), ∀aϵP – {–6 }is a rational function.
• Graph type: Asymptotes (the curves touching the axes lines).

Algebraic Functions

A function that consists of a finite number of terms involving powers and roots of independent variable x and fundamental operations such as addition, subtraction, multiplication, and division is known as an algebraic equation.

For Example,

f(x)=5x3−2x2+3x+6, g(x)=3x+4(x−1)2.

Cubic Function

A cubic polynomial function is a polynomial of degree three and can be expressed as;

F(x) = ax³ + bx² + cx + d and a is not equal to zero.

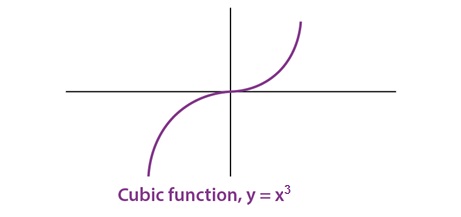
In other words, any function in the form of f(x) = ax³ + bx² + cx + d, where a, b, c, d∈R & a ≠ 0

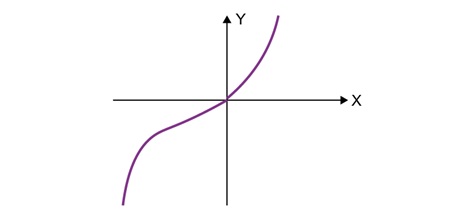
For example: y = x³

MODULUS FUNCTION:

A Function f(x) : R à R is said to be Modulus function if y=f(x) = |x| 

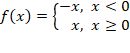
Domain of f = R

Range of f = R⁺U {0}

Codomain=R

 

If x = -5, then y = f(x) = – (-5) = 5, since x is less than zero

If x = 10, then y = f(x) = 10, since x is greater than zero

If x = 0, then y = f(x) = 0, since x is equal to zero

When x = -3 then y = |-3| = 3

When x = -2 then y = |-2| = 2

When x = -1 then y = |-1| = 0

When x = 0 then y = |0| = 0

When x = 1 then y = |1| = 1

When x = 2 then y = |2| = 2

When x = 3 then y = |3| = 3

Signum Function:

A Function f(x) : R à R is said to be signum function if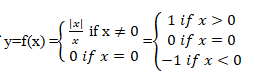  

Domain of f = R

Range of f = {-1,0,1}

Codomain=R

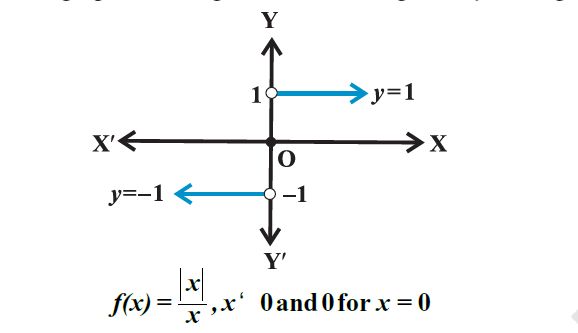
If x = -5, then y = f(x) = – 1 , since x is less than zero

If x = 5, then y = f(x) = 1 , since x is greater than zero

If x = 0, then y = f(x) = 0 , since x is equal to zero

Greatest Integer Function:

A  Function f(x) : R à R is said to be greatest integer function if y=f(x)=[x]

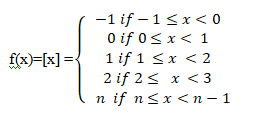
or

The function f: R , R defined by f(x) = [x], x R assumes the value of the greatest integer, less

than or equal to x. Such a function is called the greatest integer function.

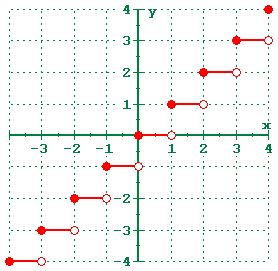
Domain of f = R

Range of f = Z

Codomain=R

[1.15] = 1  , [1.9] =1

[4.56567] = 4  , [4.99] = 4

[50] = 50

[-3.010] = -4

Greatest Integer Function Properties

•  [x] = x, where x is an integer
• [x + n] = [x] + n, where n ∈ Z
• [-x] = –[x], if x ∈ Z
• [-x] =-[x] – 1, if x ∉ Z
• If [f(x)] ≥ Y, then f(x) ≥ Y

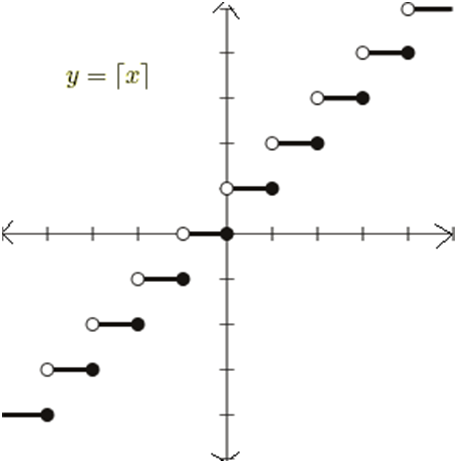
Smallest Integer Function:

Ceiling function f(x) = ⌈x⌉ and  floor function f(x)=⌊x ⌋

f(x) = ⌊x⌋ = Largest Nearest Integer of specified value

f(x) = ⌈x⌉ = Least Nearest successive Integer of specified value

A  Function f(x) : R à R is said to be Smallest integer function if y=f(x)= ⌊x ⌋

 

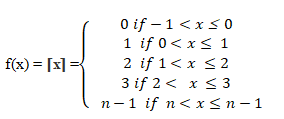
Domain of f = R

Range of f = Z

Codomain=R

Properties:

• ⌈x⌉ + ⌈y⌉ – 1 ≤ ⌈x + y⌉ ≤ ⌈x⌉ + ⌈y⌉
• ⌈x + a⌉ = ⌈x⌉ + a
• ⌈x⌉ = a; iff x ≤ a < x + 1
• ⌈x⌉ = a; iff x – 1 < a ≤ x
• a < ⌈x⌉ iff a < x
• a ≤ ⌈x⌉ iff x < a

Step Function:

A step function (also called as staircase function) is defined as a piecewise constant function, that has only a finite number of pieces. In other words, a function on the real numbers can be described as a finite linear combination of indicator functions of given intervals.

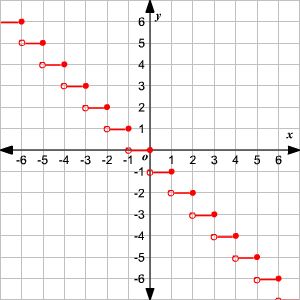
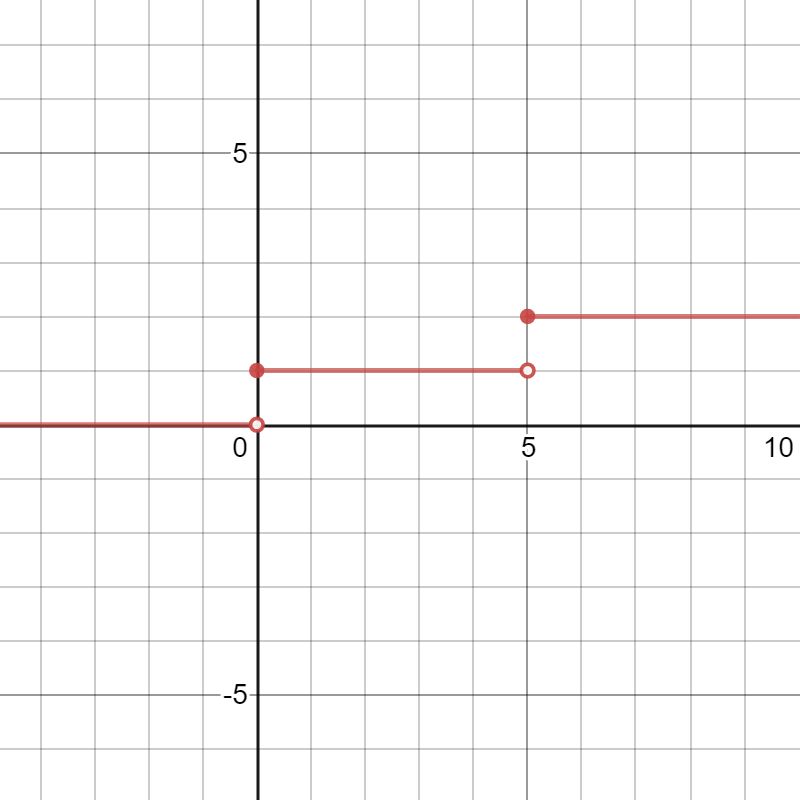
Domain of f = referred to as the set of input values

Range of f = referred to as the set of output values generated for the domain (input values)

Properties

The important properties of step functions are given below:

• The sum or product of two-step functions is also a step function.
• If a step function is multiplied by a number, then the result produced is again a step function. That indicates the step functions create an algebra over the real numbers
• A step function can take only a finite number of values
• Piecewise linear function is the definite integral of a step function

Indicator function / Characteristic function: 

An indicator function or a characteristic function of a subset of a set is a function that maps elements of the subset to one, and all other elements of the set to zero. The indicator function of a subset A of a set X maps X to the two-element set 

{ 0,1}; c_A(x)=1 if an element {displaystyle x}in X belongs to A

and c_A(x)=0 if x does not belong to A.

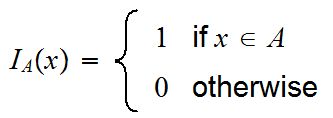
It may be denoted as 1_A , by I_A or by c_A

The indicator function of a subset, that is the function

c _A : X à {0,1}

which for a given subset A of X, has value 1 at points of A and 0 at points of X − A.

Fractional Part Function:

The fractional part function is the difference between a number and its integer part.

A  Function f(x) : R à R is said to be fractional part function if  y = f(x) = {x} = x- [x]

Domain of a fractional function is all the real numbers except the roots of denominator of the fraction.

Codomain =R

Range = [0,1)

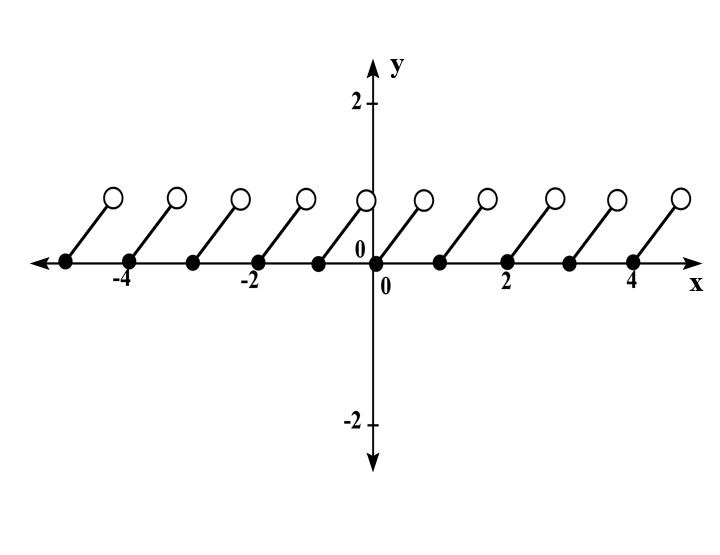
{1}=1−[1]=1-1=0.

Properties;

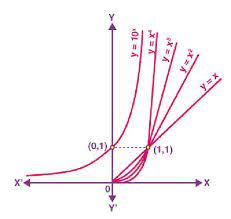
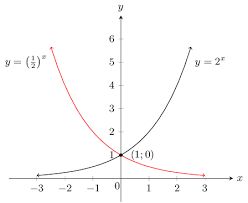
Exponential Function:

For a > 1, the Exponential of b to base a is x if y =f(x)=  a^x = b. Thus, The  function is known as Exponential function

Exponential function having base 10 is known as a common exponential function.

i.e.,y=f(x)= 10^x

Exponential function having base e is known as a Natural exponential function.

y=f(x)= e^x

Domain =R

Codomain =R⁺

Range = R⁺

Properties:

• The graph passes through the point (0,1).
• The domain is all real numbers
• The range is y>0
• The graph is increasing
• The graph is asymptotic to the x-axis as x approaches negative infinity
• The graph increases without bound as x approaches positive infinity
• The graph is continuous
• The graph is smooth

If a>0, and  b>0, the following hold true for all the real numbers x and y:

• • a^x a^y = a^x+y
  • a^x/a^y = a^x-y
  • (a^x)^y = a^xy
  • a^xb^x=(ab)^x
  • (a/b)^x= a^x/b^x
  • a⁰=1
  • a^-x= 1/ a^x

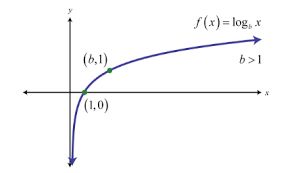
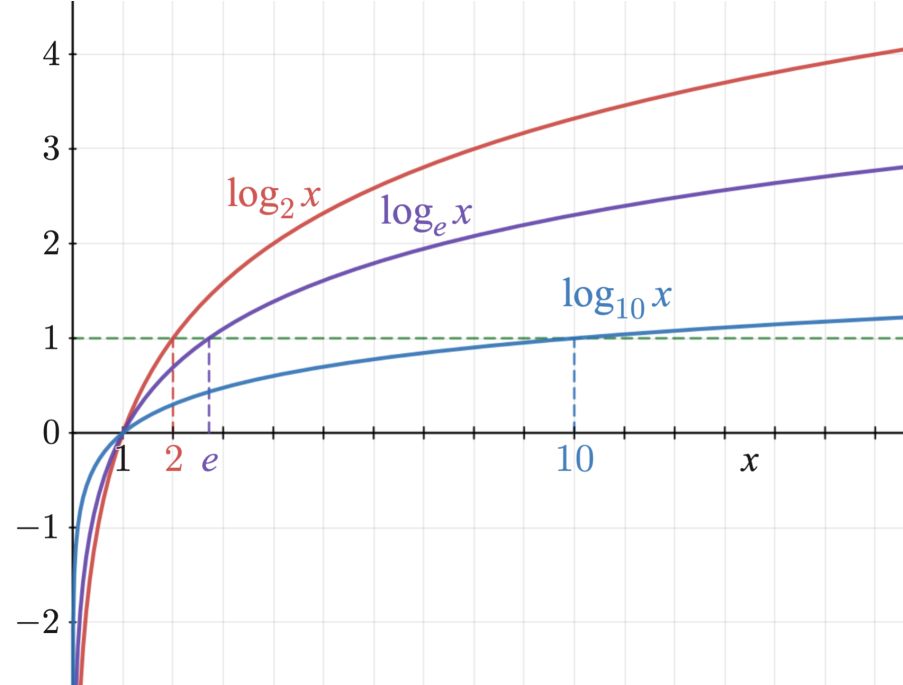
Logarithmic Function:

For a > 1, the logarithm of b to base a is x if a^x = b. Thus, log_a b = x if a^x = b. This function is known as logarithmic function.

logarithm function having base 10 is known as a common logarithm function.

i.e.,y=f(x)= log₁₀ x

logarithm function having base e is known as a Natural logarithm function.

y=f(x)= log_e x= lnx

Domain = R⁺

Codomain =R

Range = R

Properties:

• The graph passes through the point (1,0).
• The domain is all +ve real numbers
• Log_ap = α, log_bp = β and log_ba = µ, then a^α = p, b^β = p and b^µ = a
• Log_bpq = Log_bp + Log_bq
• Log_bp^y = ylog_bp
• Log_b (p/q) = log_bp – log_bq
• When we plot the graph of log functions and move from left to right, the functions show increasing behaviour.
• The graph of log function never cuts the x-axis or y-axis, though it seems to tend toward them.

Sinusoidal Function:

A sinusoidal function is a function using the sine function. The basic form of a sinusoidal function is  where A is the amplitude or height of our function, B is the change in period defined by   the horizontal shift, and D the vertical shift.​​​​​​​

The sine and cosine functions have several distinct characteristics:

​​​​​​​

Even and Odd Function:

The definition of even and odd functions:

 Even function: A function, f(x) is even if f(x) = f(-x) 

Example:f(x)=cosx

 f(-x)=cos(-x)= cosx=f(x)

so f is even function.

examples of even functions are x⁴, cot x, y = x², etc.

Odd Function: A function, f(x) is odd if f(x) = -f(x) For example,

Check if function is even or odd: f (x) = tan x

f(-x)=tan(-x)= -tanx=-f(x)

so f is odd function.

The polynomial function f(x)=x2+x4+x6 is even. The polynomial function f(x)=x+x3+x5 is odd

Periodic Function:

A function y= f(x) is said to be a periodic function if there exists a positive real number P such that f(x + P) = f(x), for all x belongs to real numbers. The least value of the positive real number P is called the fundamental period of a function.

This fundamental period of a function is also called the period of the function, at which the function repeats itself. f(x + P) = f(x)

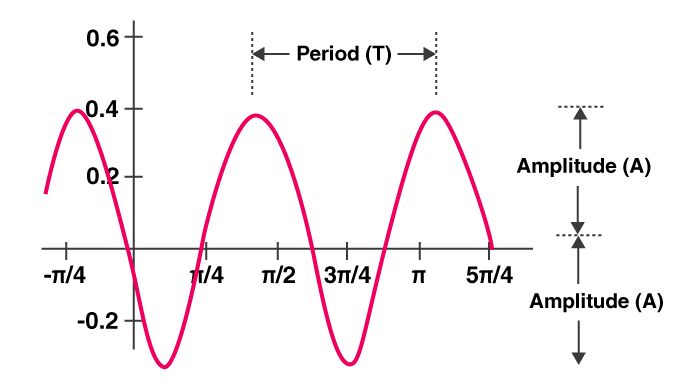
The period of the sine ,cosine function is 2π (units). All the trigonometric functions are periodic functions.

Composite Function:

Let f : A → B and g : B → C be two functions. Then the composition of f and g, denoted by g ∘ f, is defined as the function g ∘ f : A → C given by g ∘ f (x) = g(f (x)), ∀ x ∈ A.

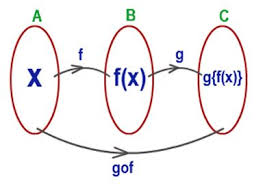
The composite function gof(x) is read as “g of f of x”. If f(x)and g(x) are two functions then fog(x), gof(x), gog(x) and fof(x) are composite functions.

• fog(x) = f(g(x))
• gof(x) = g(f(x))
• gog(x) = g(g(x))
• fof(x) = f(f(x))
• fogoh(x) = f(g(h(x)))
• fofof(x) = f(f(f(x)))

The order of the function is important in a composite function since (fog)(x) is not equal to (gof)(x).