4. Derivatives ,Existence of Derivative and Algebra of Derivatives

Derivatives, Existence of Derivative and Algebra of Derivatives

Definition: Suppose f is a real valued function and a is a point in its domain of definition. The derivative of f at a is defined by

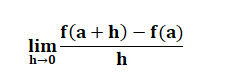
provided this limit exists. Derivative of f (x) at a is denoted by f’(a). Observe that f’(a) quantifies the change in f(x) at a with respect to x.

It is called first principle method or abinitio method or definition method.

Derivatives are defined as the varying rate of change of a function with respect to an independent variable. The derivative is primarily used when there is some varying quantity, and the rate of change is not constant. The derivative is used to measure the sensitivity of one variable (dependent variable) with respect to another variable (independent variable).

The process of finding the derivative is called differentiation. The inverse process is called anti-differentiation. Let’s find the derivative of a function y = f(x). 

Example: Find the derivative of the following functions from first principle (x−1)(x−2)

Solution

Let  f(x)=(x−1)(x−2)
Thus according to first principle,

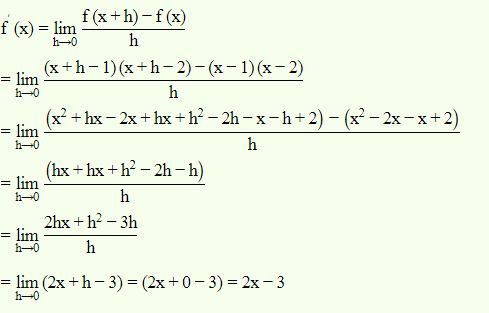
Example  Find the derivative of f(x) = 10x.

Solution Since

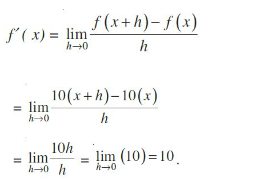
Example  Compute the derivative of tan x.

Solution Let f(x) = tan x. Then f’(x) =

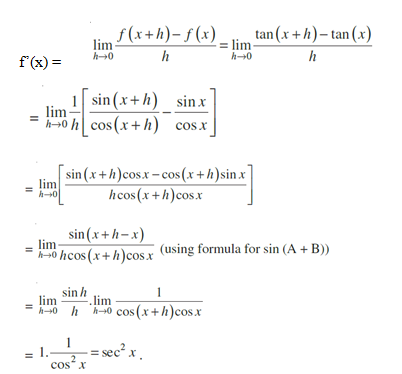
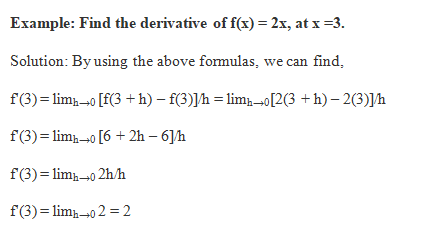
Note:

1. D(y) or D[f(x)] is called Euler’s notation.
2. dy/dx is called Leibniz’s notation.

F’(x) is called Lagrange’s notation

Formula

1. If f(x) = tan (x), then f'(x) = sec²x
2. If f(x) = cos (x), then f'(x) = -sin x
3. If f(x) = sin (x), then f'(x) = cos x
4. If f(x) = ln(x), then f'(x) = 1/x
5. If f(x) = e^x, then f'(x) = e^x
6. If f(x) = xⁿ, where n is any fraction or integer, then f'(x) = nx^n-1
7. If f(x) = k, where k is a constant, then f'(x) = 0

Algebra of derivative of functions:

Let  two functions of x be  u(x) and v(x)

The basic differentiation rules that need to be followed are as follows:

[1] Sum and Difference Rule

If the function is the sum or difference of two functions, the derivative of the functions is the sum or difference of the individual functions, i.e.,

If f(x) = u(x) ± v(x) then, f'(x) =(d/dx)[u(x)+v(x)] =u'(x) ± v'(x)

[2] Product Rule

If the function f(x) is product of two functions u(x) and v(x), the derivative of the function is,

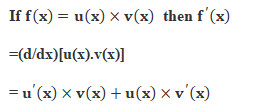
[3] Quotient Rule

If the function f(x) is in the form of two functions [u(x)]/[v(x)], the derivative of the function is

[4] Chain Rule

If a function y = f(x) = g(u) and if u = h(x), then the chain rule for differentiation is defined as,

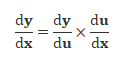
Example: Differentiate f(x) = 6x³ – 9x + 4 with respect to x.
Solution: Given: f(x) = 6x³ – 9x + 4

On differentiating both the sides w.r.t x, we get;

f'(x) = (3)(6)x² – 9

f'(x) = 18x² – 9

General Derivative Formulas