- Books Name
- AMARENDRA PATTANAYAK Mathmatics Book
- Publication
- KRISHNA PUBLICATIONS
- Course
- CBSE Class 11
- Subject
- Mathmatics
Chapter 12
Introduction to Three-Dimensional Geometry
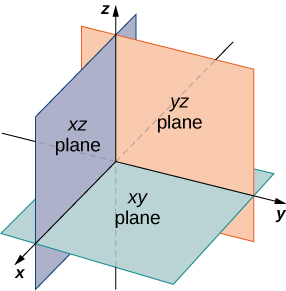
Coordinate axes and planes in 3D:
Let Consider three planes intersecting at a point O such that these three planes are mutually perpendicular to each other.
These three planes intersect along the lines XOX, YOY and ZOZ, called the x, y and z-axes, respectively.
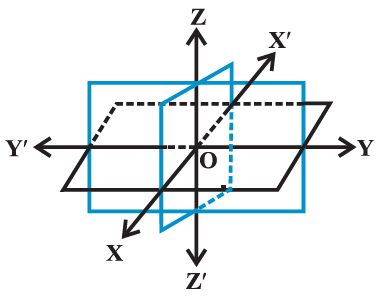
The point O is called the origin of the coordinate system. The three coordinate planes divide the space into eight parts known as octants. These octants could be named as XOYZ, XOYZ, XOYZ, XOYZ, XOYZ, XOYZ, XOYZ and XOYZ. and denoted by I, II, III,.. ..., VIII , respectively.
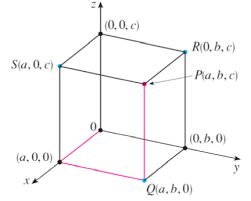
Coordinates of a Point in Space
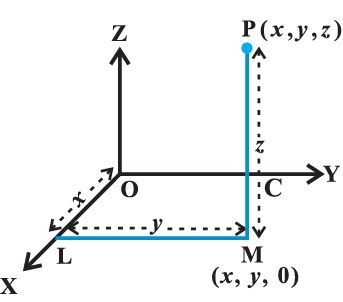
Let OA = x, OB = y and OC = z. Then, the point P will have the coordinates x, y and z and we write P (x, y, z). Conversely, given x, y and z, we locate the three points A, B and C on the three coordinate axes. Through the points A, B and C we draw planes parallel to the YZ-plane, ZX-plane and XY-plane,respectively.
In three-dimensional geometry, the coordinates of a point P is always written in the form of P(x, y, z), where x, y and z are the distances of the point, from the YZ, ZX and XY-planes.
- The coordinates of any point at the origin is (0,0,0)
- The coordinates of any point on the x-axis is in the form of (x,0,0)
- The coordinates of any point on the y-axis is in the form of (0,y,0)
- The coordinates of any point on the z-axis is in the form of (0,0,z)
- The coordinates of any point on the XY-plane is in the form (x, y, 0)
- The coordinates of any point on the YZ-plane is in the form (0, y, z)
- The coordinates of any point on the ZX-plane is in the form (x, 0, z)
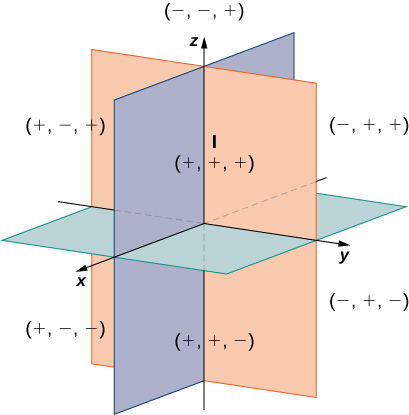
Sign of Coordinates in Different Octants:
The sign (+ or -) of the coordinates of a point determines the octant in which the point lies.

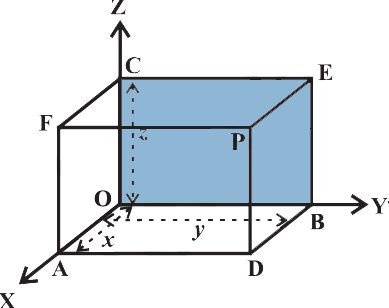
Example: In Fig 12.3, if P is (2,4,5), find the coordinates of F.
Solution For the point F, the distance measured along OY is zero. Therefore, the
coordinates of F are (2,0,5).
Example Find the octant in which the points (–3,1,2) and (–3,1,– 2) lie.
Solution From the Table 12.1, the point (–3,1, 2) lies in second octant and the point
(–3, 1, – 2) lies in octant VI.

 KRISHNA PUBLICATIONS
KRISHNA PUBLICATIONS
