Chapter 16: Probability

Chapter 16

Probability

Probability and Random experiments:

A probability is simply a number between 0 and 1 that measures the uncertainty of a particular event.

Although many events are uncertain, we possess different degrees of belief about the truth of an uncertain event.

Many events cannot be predicted with total certainty. We can predict only the chance of an event to occur i.e. how likely they are to happen, using it. Probability can range in from 0 to 1, where 0 means the event to be an impossible one and 1 indicates a certain event.

OR

Probability is the branch of mathematics concerning numerical descriptions of how likely an event is to occur, or how likely it is that a proposition is true. The probability of an event is a number between 0 and 1, where, roughly speaking, 0 indicates impossibility of the event and 1 indicates certainty.

For example, most of us are pretty certain of the statement "the sun will rise tomorrow", and pretty sure that the statement "the moon is made of green cheese" is false.

For example, when we toss a coin, either we get Head OR Tail, only two possible outcomes are possible (H, T). But if we toss two coins in the air, there could be three possibilities of events to occur, such as both the coins show heads or both show tails or one shows heads and one tail, i.e.(H, H), (H, T),(T, T).

The Classical view of a Probability

Suppose that we observe some phenomena (say, the rolls of two dice) where the outcome is random. Suppose we can write down the list of all possible outcomes, and we believe that each outcome in the list has the same probability. Then the probability of each outcome will be

P(outcome)=1/(number of outcomes)

The Frequency View of a Probability

The classical view of probability is helpful only when we can construct a list of outcomes of the experiment in such a way where the outcomes are equally likely.

The frequency interpretation of probability can be used in cases where outcomes are equally likely or not equally likely.

This view of probability is appropriate in the situation where we are able to repeat the random experiment many times under the same conditions.

An Experiment is defined as a process whose result is well defiened

Two types of Experiment:

1. Deterministic Experiment
2. Random Experiment

Deterministic Experiment:

It is an Experiment whose outcomes can be predicted with certainty under identical conditions.

Example: When we heat water it will evaporate

Example: When we toss a two headed coin we will get a head.

Random Experiment

It is an experiment whose all possible outcomes are known but it is not possible to predict the exact outcomes in advance.

Or

A random experiment is a mechanism that produces a definite outcome that  cannot be predicted with certainty.

Example: An unbiased coin is tossed.

Example: A die is rolled.

Random Experiment always satisfies the following two conditions:

1. It has more than one possible outcomes
2. It is not possible to predict the outcome in advance.

The two possible outcomes are getting a head or a tail. The outcome of this experiment cannot be predicted before it has been performed. Furthermore, it can be conducted many times under the same conditions. Thus, tossing a coin is an example of a random experiment.

Outcome: A possible result of a random experiment is called its outcome.

Sample spaces, events and types of events, Algebra of events:

The set of all possible outcomes of a random experiment is called the sample space associated with the experiment.

Sample space is denoted by the symbol S.

Each element of the sample space is called a sample point.

 In other words, each outcome of the random experiment is also called sample point.

Example : Two coins (a one rupee coin and a two rupee coin) are tossed once.

Find a sample space.

Solution:

Heads on both coins = (H,H) = HH

Head on first coin and Tail on the other = (H,T) = HT

Tail on first coin and Head on the other = (T,H) = TH

Tail on both coins = (T,T) = TT

Thus, the sample space is S = {HH, HT, TH, TT}

Example : Consider the experiment in which a coin is tossed repeatedly until a head comes up. Describe the sample space.

Solution:

In the experiment

head may come up on the first toss, or the 2nd toss, or the 3rd toss and so on till head is obtained.

Hence, the desired sample space is  S= {H, TH, TTH, TTTH, TTTTH,...}

Event:

Any subset E of a sample space S is called an event.

Types of events:

1. Impossible and Sure Events :

The empty set f and the sample space S describe events.

In fact f is called an impossible event and S, i.e., the whole sample space is called the sure event.

Example:

let us consider the experiment of rolling a die. The associated sample space is

S = {1, 2, 3, 4, 5, 6}

Let E be the event “ the number appears on the die is a multiple of 7”.

E={} = f is an impossible event.

Let event F “the number turns up is odd or even”.

F= {1, 2, 3, 4, 5, 6} = S

Thus, the event F = S is a sure event.

1. Simple Event : If an event E has only one sample point of a sample space, it is

called a simple (or elementary) event.

In a sample space containing n distinct elements, there are exactly n simple events.

For example in the experiment of tossing two coins, a sample space is

S={HH, HT, TH, TT}

There are four simple events corresponding to this sample space. These are

E1= {HH}, E2={HT}, E3= { TH} and E4={TT}.

2. Compound Event: If an event has more than one sample point, it is called a

Compound event.

For example, in the experiment of “tossing a coin thrice” the events

E: ‘Exactly one head appeared’

F: ‘Atleast one head appeared’

G: ‘Atmost one head appeared’ etc.

are all compound events. The subsets of S associated with these events are

E={HTT,THT,TTH}

F={HTT,THT, TTH, HHT, HTH, THH, HHH}

G= {TTT, THT, HTT, TTH}

Algebra of events:

1. Complementary Event
2. The Event ‘A or B’
3. The Event ‘A and B’
4. The Event ‘A but not B’

i)  Complementary Event: For every event A, there corresponds another event Acalled the complementary event to A. It is also called the event ‘not A’.

For example, take the experiment ‘of tossing three coins’. An associated sample

Space  is S = {HHH, HHT, HTH, THH, HTT, THT, TTH, TTT}

Let  A= {HTH, HHT, THH} be the event ‘only one tail appears’

Clearly for the outcome HTT, the event A has not occurred. But we may say that the event ‘not A’ has occurred. Thus, with every outcome which is not in A, we say that ‘not A’ occurs.

Thus the complementary event ‘not A’ to the event A is

A`= {HHH, HTT, THT, TTH, TTT}

or  A¢ = {w : w Î S and w ÏA} = S – A.

ii)  The Event “ A or B  “ : Recall that union of two sets A and B denoted by A È B contains all those elements which are either in A or in B or in both.

When the sets A and B are two events associated with a sample space,

Then ‘A È B’ is the event ‘either A or B or both’. This event ‘A È B’ is also called ‘A or B’.

Therefore Event ‘ A or B ’ = A È B  = {w : w Î A or w Î B}

iii)  The Event ‘ A and B ’ : We know that intersection of two sets A Ç B is the set of

those elements which are common to both A and B. i.e., which belong to both ‘A and B’.

If A and B are two events, then the set A Ç B denotes the event ‘A and B’.

Thus, A Ç B = {w : w Î A and w Î B}

For example, in the experiment of ‘throwing a die twice’

Let A be the event ‘score on the first throw is six’ and

 B is the event ‘sum of two scores is atleast 11’ then

A = {(6,1), (6,2), (6,3), (6,4), (6,5), (6,6)}, and B = {(5,6), (6,5), (6,6)}

So  A Ç B = {(6,5), (6,6)}

Note that the set A Ç B = {(6,5), (6,6)} may represent the event ‘the score on the first throw is six and the sum of the scores is atleast 11’.

iii)  The Event ‘A but not B’ : We know that A–B is the set of all those elements

which are in A but not in B. Therefore, the set A–B may denote the event ‘A but not B ’.We know that  A – B = A Ç B´

Example:  Consider the experiment of rolling a die. Let A be the event ‘getting a prime number’, B be the event ‘getting an odd number’. Write the sets representing the events

(i) Aor B (ii) A and B (iii) A but not B (iv) ‘not A’.

Solution:  Here S = {1, 2, 3, 4, 5, 6}, A = {2, 3, 5} and B = {1, 3, 5}

Obviously

(i) ‘A or B’ = A È B = {1, 2, 3, 5}

(ii) ‘A and B’ = A Ç B = {3,5}

(iii) ‘A but not B’ = A – B = {2}

(iv) ‘not A’ = A¢ = {1,4,6}

Mutually exclusive events:

Two events A and B are called mutually exclusive events if the occurrence of any one of them excludes the occurrence of the other event, i.e., if they can not occur simultaneously. In this case the sets A and B are disjoint.

Example:

In the experiment of rolling a die, a sample space is

S = {1, 2, 3, 4, 5, 6}. Consider events, A ‘an odd number appears’ and B ‘an even

number appears’

Clearly the event A excludes the event B and vice versa.

In other words, there is no outcome which ensures the occurrence of events A and B simultaneously.

Here A = {1, 3, 5} and B = {2, 4, 6}

Clearly A Ç B = f, i.e., A and B are disjoint sets.

So two events A and B are called mutually exclusive events.

Note: Simple events of a sample space are always mutually exclusive.

if E1, E2, ..., En are n events of a sample space S and ifE₁ È E₂ È E₃ È E₄ È...... È E_n = S

then E1, E2, ...., En are called exhaustive events.

In other words, events E1, E2, ..., En are said to be exhaustive if atleast one of them necessarily occurs whenever the experiment is performed.

Further, if Ei Ç Ej = f for i ¹ j i.e., events Ei and Ej are pairwise disjoint and

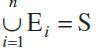
, then events E1, E2, ..., En are called mutually exclusive and exhaustive events.

Example :  A coin is tossed three times, consider the following events.

A: ‘No head appears’, B: ‘Exactly one head appears’ and C: ‘Atleast two heads

appear’.

Do they form a set of mutually exclusive and exhaustive events?

Solution: The sample space of the experiment is

S = {HHH, HHT, HTH, THH, HTT, THT, TTH, TTT}

and A = {TTT}, B = {HTT, THT, TTH}, C = {HHT, HTH, THH, HHH}

Now

A È B È C = {TTT, HTT, THT, TTH, HHT, HTH, THH, HHH} = S

Therefore, A, B and C are exhaustive events.

Also, A Ç B = f, A Ç C = f and B Ç C = f

Therefore, the events are pair-wise disjoint, i.e., they are mutually exclusive.

Hence, A, B and C form a set of mutually exclusive and exhaustive events.

Axiomatic Approach to probability:

Axiomatic probability is a unifying probability theory in Mathematics. The axiomatic approach to probability sets down a set of axioms that apply to all of the approaches of probability which includes frequentist probability and classical probability. These rules are generally based on Kolmogorov's Three Axioms.

Axiomatic approach is another way of describing probability of an event. In this approach some axioms or rules are depicted to assign probabilities.

Let S be the sample space of a random experiment.

The probability P is a real valued function whose domain is the power set of S and range is the interval [0,1] satisfying the following axioms

1. For any event E, P (E) ³ 0
2.  (ii) P (S) = 1
3. If E and F are mutually exclusive events, then P(E È F) = P(E) + P(F).

P (E È f) = P (E) + P (f)

 P(E) = P(E) + P (f)

i.e. P (f) = 0.

Let S be a sample space containing outcomes w₁, w₂, ..., w_n .

i.e., S = {w₁, w₂, ..., w_n}

It follows from the axiomatic definition of probability that

(i) 0 £ P (w_i) £ 1 for each w_i Î S

(ii) P (w₁) + P (w₂) + ... + P (w_n) = 1

(iii) For any event A, P(A) = å P(w_i ), w_i Î A.

Example: A coin tossing

S={H,T}

P(H)= ½  ,P(T) = ½

i.e., each number is neither less than zero nor greater than 1

and P(H) + P(T) = ½ + ½  = 1

In fact, we can assign the numbers p and (1 – p) to both the outcomes such that

0 £ p £ 1 and P(H) + P(T) = p + (1 – p) = 1

This assignment, too, satisfies both conditions of the axiomatic approach of probability.

Hence, we can say that there are many ways (rather infinite) to assign probabilities to outcomes of an experiment.

Probability of an event

The probability of an event is the proportion (relative frequency) of times that the event is expected to occur when an experiment is repeated a large number of times under identical conditions.

Where,

• P(A) is the probability of an event “A”
• n(A) is the number of favourable outcomes
• n(S) is the total number of events in the sample space

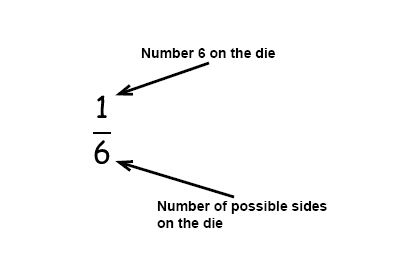
What is the probability to get a 6 when you roll a die?

A die has 6 sides, 1 side contain the number 6 that give us 1 wanted outcome in 6 possible outcomes.

Example:

Let us consider another experiment of ‘tossing a coin “twice”

The sample space of this experiment is S = {HH, HT, TH, TT}

P(HH) =1/4  , P(HT) = 1 / 7 , P(TH) = 2 / 7 ,  P(TT) = 9 / 28

The probability of the event E: ‘Both the tosses yield the same result’.

Here E = {HH, TT}

Now P(E) = S P(wi), for all wi Î E

= P(HH) + P(TT) = 1/4  + 9 / 28  = 4 /7

For the event F: ‘exactly two heads’, we have F = {HH}

P(F) = P(HH) = ¼

Probabilities of equally likely outcomes: Let a sample space of an experiment be

S = {w1, w2,..., wn}.

Let all the outcomes are equally likely to occur, i.e., the chance of occurrence of each

simple event must be same.

i.e. P(wi) = p, for all wi Î S where 0 £ p £ 1

Since  i.e., P(w1)+ P(w2)+ P(w3) + P(w4) + P(w5)+.....+ P(wn) = p + p + ... + p (n times) = 1

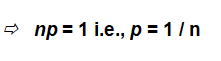
Let S be a sample space and E be an event, such that n(S) = n and n(E) = m. If each outcome is equally likely, then it follows that

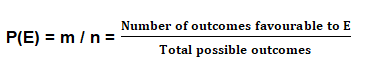
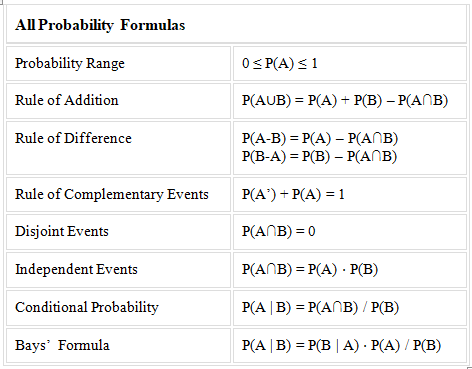
Basic Probability Formulas

Let A and B are two events. The probability formulas are listed below:

Probability of “not”, “and” and “or” events

If the events A and B are not mutually exclusive,

 the probability is: P(A or B) = P(A) + P(B) – P(A and B).

and

P(not A) = 1 – P(A)

Either/or probability refers to the probability that one event or the other will occur. For example, what is the probability that you will draw a Jack or a three from a normal deck of cards? Or, what is the probability that you will roll a 3 or a 5 when rolling a normal 6-sided die? To solve this type of probability problem, here is the formula you will use:

P(A or B) = P(A) + P(B)

To find the probability of each event, simply divide the amount of favorable events by the amount of total events. A favorable event is an event that you want to occur. In the earlier card question, the favorable event is drawing either a Jack or a three. The total number of events is the total number of things that could occur, whether favorable or not.

So, to continue on and solve this card drawing question, we have determined that A is the probability of drawing a Jack, and B is the probability of drawing a three.

There are 4 Jacks in a normal deck of cards, so the number of favorable events (drawing a Jack) is 4. The total number of events is 52 since there are 52 cards in a deck of cards. This means that the probability of drawing a Jack is 4/52, which can be reduced to 1/13.

P(B), or the probability of drawing a three, is also 1/13 because there are 4 threes in a deck of cards and, as before, there are 52 total cards in the deck.

To finish answering the question and find the probability of drawing either a Jack or a three, we use the equation P(A or B) = P(A) + P(B). P(A or B) is equal to 1/13 + 1/13, which is 2/13

To solve the dice question mentioned earlier, follow the same steps. P(A), or the probability of rolling a 3, is 1/6. There is one 3 (the favorable event) and 6 sides on the die (the total events).

P(B) is the probability of rolling a 5 and it's the same, 1/6. Therefore, the probability of rolling either a 3 or a 5 is P(A or B) is equal to 1/6 + 1/6, which is 2/6, or 1/3.

These events are called non-overlapping events, or events that are independent of each other. There are also overlapping events, which are events that are not independent of each other.

Example :  A die has sides numbered 1-9. You roll the die. What is the probability that the number you obtain is odd or prime.

Solution: Let A be the event that the number is odd and B the event that the number is a prime.

Then A and B are overlapping events 

since a number can be both prime and odd from among the numbers 1-9.

The odd numbers in 1-9 are 1, 3, 5, 7 and 9 (total of five), while the prime numbers in 1-9 are 1, 3, 5 and 7 (total of four). Hence the numbers in 1-9 that are odd AND prime are 1, 3, 5 and 7 (total of four).

Hence:

P(A or B) = P(A) + P(B) - P(A and B)

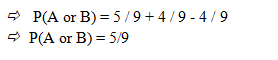
Example : A box has 6 red marbles, 7 blue marbles and 8 green marbles. You draw one marble at random from the box. What is the probability that the marble is red or green?

Solution:

Let A be the event that the marble is red and B be the event that the marble is green.

Since A and B are not overlapping, that marble cannot be both red AND green. So we get the probability as follows:

P(A or B) = P(A) + P(B)

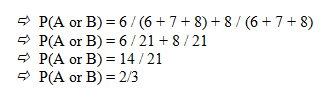
Example : What is the probability that a card taken from a standard deck, is an Ace?

Solution:

Total number of cards a standard pack contains = 52

Number of Ace cards in a deck of cards = 4

So, the number of favourable outcomes = 4

Now, by looking at the formula,

Probability of selecting an ace from a deck is,

P(Ace) = (Number of favourable outcomes) / (Total number of favourable outcomes)

P(Ace) = 4/52

= 1/13

So we can say that the probability of getting an ace is 1/13.

Example : Calculate the probability of getting an odd number if a dice is rolled.

Solution:

Sample space (S) = {1, 2, 3, 4, 5, 6}

n(S) = 6

Let “E” be the event of getting an odd number, E = {1, 3, 5}

n(E) = 3

So, the Probability of getting an odd number is:

P(E) = (Number of outcomes favorable)/(Total number of outcomes)

= n(E)/n(S)

= 3/6

= ½

Example : Two students Anil and Ashima appeared in an examination. The probability that Anil will qualify the examination is 0.05 and that Ashima will qualify the examination is 0.10. The probability that both will qualify the examination is 0.02. Find the probability that

(a) Both Anil and Ashima will not qualify the examination.

(b) Atleast one of them will not qualify the examination and

(c) Only one of them will qualify the examination.

Solution: Let E and F denote the events that Anil and Ashima will qualify the examination,

respectively.

Given that P(E) = 0.05, P(F) = 0.10 and P(E Ç F) = 0.02.

Then

1. The event ‘both Anil and Ashima will not qualify the examination’ may be expressed as

E´ Ç F´.

Since, E´ is ‘not E’, i.e., Anil will not qualify the examination and F´ is ‘not F’,

i.e., Ashima will not qualify the examination.

Also E´ Ç F´ = (E È F)´ (by Demorgan's Law)

Now P(E È F) = P(E) + P(F) – P(E Ç F)

or P(E È F) = 0.05 + 0.10 – 0.02 = 0.13

Therefore P(E´ Ç F´) = P(E È F)´ = 1 – P(E È F) = 1 – 0.13 = 0.87

(b) P (atleast one of them will not qualify)

= 1 – P(both of them will qualify)

= 1 – 0.02 = 0.98

(c) The event only one of them will qualify the examination is same as the event either (Anil will qualify, and Ashima will not qualify) or (Anil will not qualify and Ashima will qualify)

i.e., E Ç F´  or  E´ Ç F,  where E Ç F´ and E´ Ç F are mutually exclusive.

Therefore, P(only one of them will qualify) = P(E Ç F´ or E´ Ç F)

=  P(E Ç F´) + P(E´ Ç F) = P (E) – P(E Ç F) + P(F) – P (E Ç F)

=  0.05 – 0.02 + 0.10 – 0.02 = 0.11

Example : If A, B, C are three events associated with a random experiment,

prove that

P(AÈBÈC) = P(A) + P(B) + P(C) - P(AÇB) - P(AÇC) – P ( B Ç C) + P ( A Ç B Ç C)

Solution: Consider E = B È C

so that

P (A È B È C ) = P (A È E )

= P(A) + P(E) - P(A ÇE) ............... (1)

Now

P(E) = P(BÈC) = P(B) + P(C) − P(BÇC) ... ……. (2)

Also AÇE = AÇ(BÈC) = (A ÇB)È(AÇC) [using distribution property of

intersection of sets over the union].

Thus

P(A ÇE) = P(A ÇB) + P(A ÇC)– P [(AÇB)Ç(AÇC)]

= P(AÇ B) + P(A ÇC) – P[A ÇBÇC] .................... (3)

Using (2) and (3) in (1), we get

P[AÈ BÈC] = P(A) + P(B) + P(C) - P(BÇC)– P(AÇ B) - P(A ÇC) + P(A ÇBÇC)